剪张源约束的井中微地震震源机制反演方法
2020-03-02刘英昌陈学国
唐 杰 李 聪 刘英昌 陈学国
(①中国石油大学(华东)地球科学与技术学院,山东青岛 266580;②中国石化胜利油田分公司勘探开发研究院,山东东营 257015)
0 引言
本文首先介绍了基于剪张源约束的微地震震源机制反演的方法原理,然后通过理论模型记录测试、分析了应用效果。
1 井中微地震震源机制反演
传统地震震源机制反演通常使用 P 波和 S 波振幅,检波器布设于地表。在水力压裂微地震监测中,经常在井中设置检波器阵列,这种检波器分布具有非常有限的覆盖范围,对震源机制反演提出了挑战。
1.1 矩张量反演方法(MTI)
微地震震源机制可用矩张量的形式表示
(1)
式中:M为对称矩阵,满足Mij=Mji,其中独立元素有6个,Mij表示沿着±i方向大小相等并且在j方向相距无限小的力偶(i、j=1,2,3);M0为地震矩幅度。
均匀各向同性介质中的波场满足[20-21]
(2)

忽略f,式(2)变为
d=Gm
式中:d为包含N个振幅的矢量;G为格林矩阵,表示震源与检波器间的振幅变化;m为地震矩矢量,包含矩张量的6个独立参数。这样通过
m=G-1d
反演矩张量,但求解过程中需要更多的观测数据,此时方程为超定方程,可用广义逆G-g代替G-1
m=G-gd=(GTG)-1GTd
(3)
由于实际数据中含有噪声,因此需要6个以上的振幅值正确求解m。反演可单独使用P波、S波振幅或者联合使用P波、S波振幅。

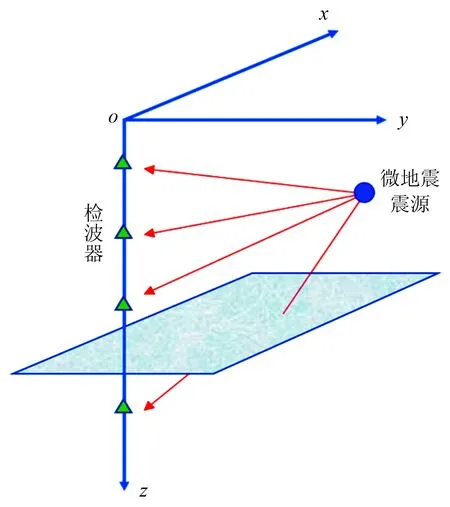
图1 分布于源到垂直井检波器的射线
1.2 剪张源约束反演方法(STI)
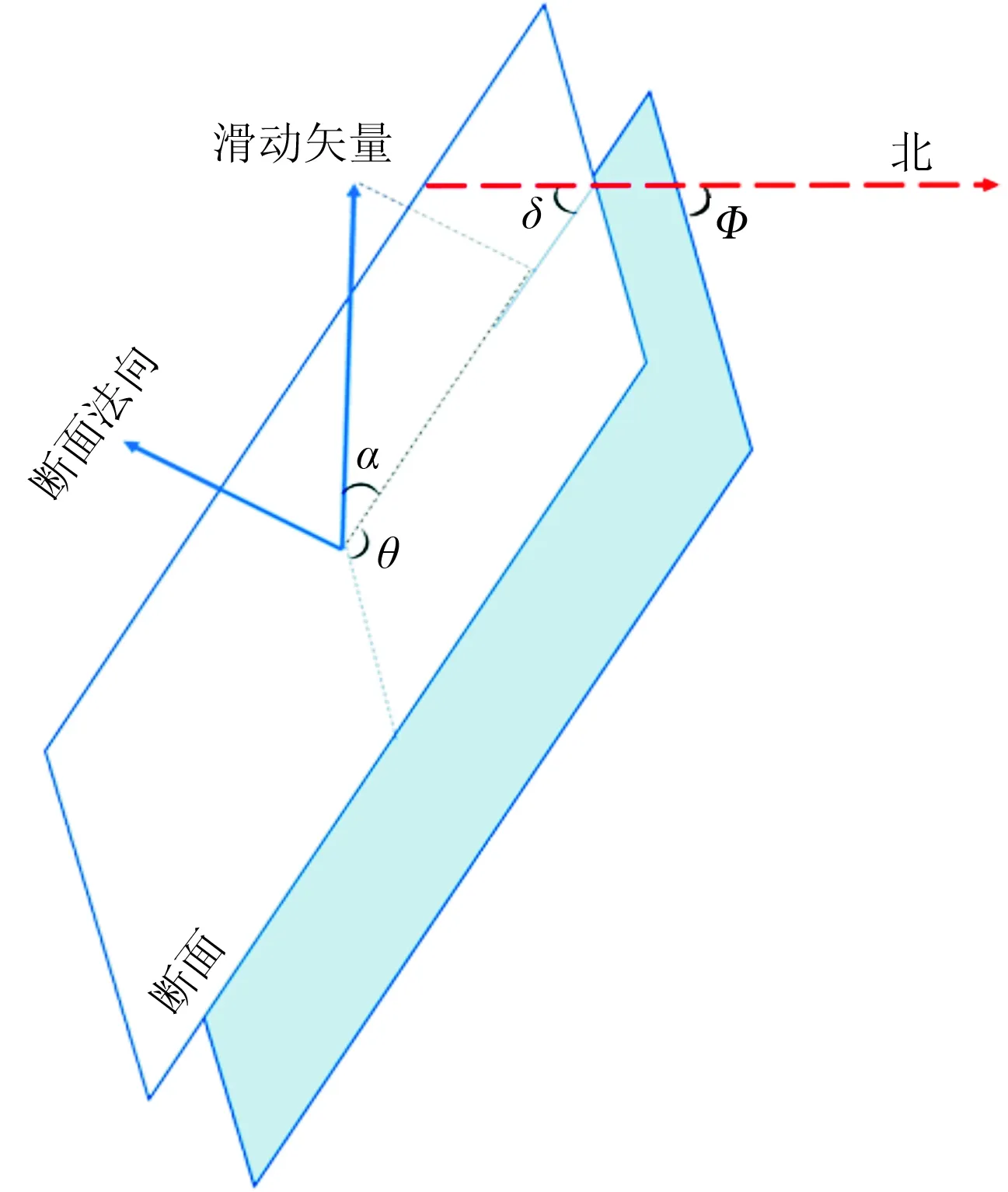
图2 混合剪切滑动和张裂的剪张源模型
为了实现井数较少情况下的反演,可以引入剪张源约束。图2为混合剪切滑动和张裂的剪张源模型,震源机制可以用走向角Φ、倾角δ、滑动角θ和张裂角α表征[24],通过这些角度可以获得剪张源的源张量D[25]。对于各向同性介质矩张量与源张量间满足[26]
Mij=λDkkδij+2μDij
(4)
式中:λ和μ为拉梅系数; δij为克罗内克函数,当i=j时,δij=1,当i≠j时,δij=0,k=1、2、3。
图3为振幅沙滩球、P波辐射花样。由图可见:在走滑情况下,Φ=45°、δ=90°、θ=180°; 在倾滑情况下,Φ=45°、δ=90°、θ=90°;震源机制沙滩球和辐射花样随着张裂角α的变化而变化。
对微地震震源矩张量M采用特征值分解法分解为双力偶部分MDC、补偿线性矢量偶极成分MCLVD和各向同性部分MISO[27]
M=MISO+MCLVD+MDC
(5)
图4为MISO、MDC、MCLVD的P波辐射花样,可见极性和波瓣分布呈明显差异。
本文研究了矩张量反演(MTI)和剪张源约束反演(STI)。MTI采用线性反演方法; STI采用非线性反演方法,将矩张量限制为描述剪张源的矩张量,减少了反演参数,鲁棒性更强。文中的STI采用信赖域反演算法,通过给定一个“信赖域半径”直接确定位移,并以当前迭代点为中心形成一个信赖域,并在其中求得最优解,产生的新迭代点具有整体收敛性。通过迭代运算求解非线性优化问题,把最优化问题转化为一系列简单的局部寻优问题,从给定的初始解出发,通过逐步迭代、不断改进,直至获得满意的最优解。

图3 振幅沙滩球(上)、P波辐射花样(下)
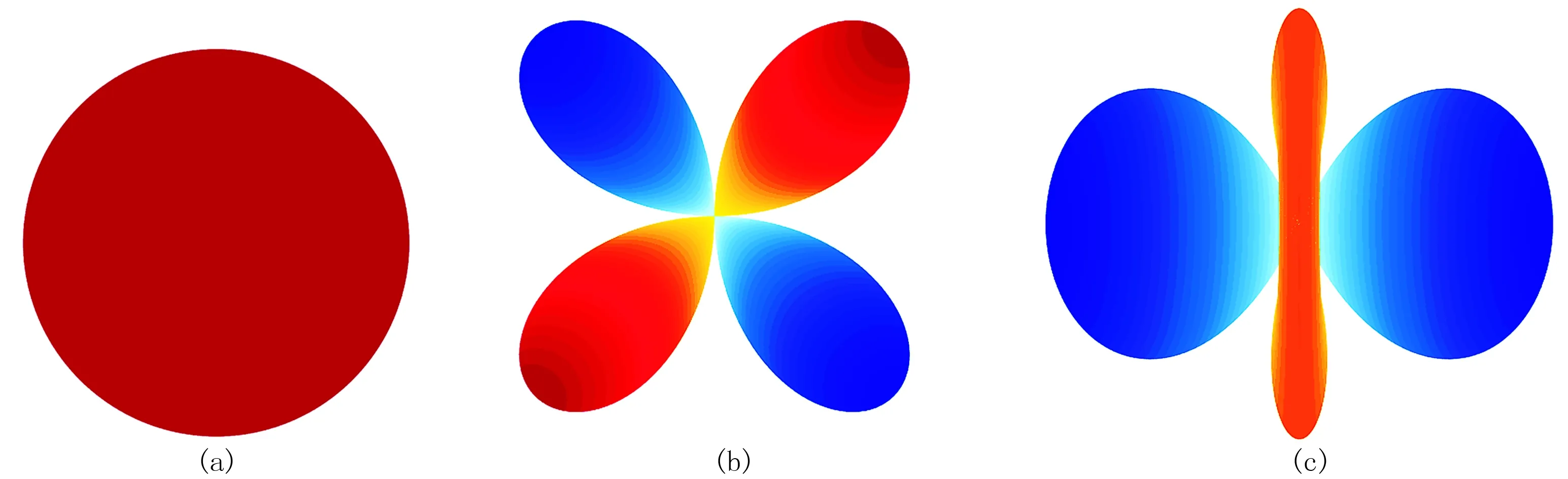
图4 MISO(a)、MDC(b)、MCLVD(c)的 P波辐射花样
2 STI测试分析
2.1 模型分析
图5为模型观测系统、合成记录及沙滩球。由图可见,无论采用三井还是单井数据,通过STI都能获得较高精度的反演结果(图5g、图5h)。
2.2 基于无噪振幅数据的反演
首先利用精确介质模型和精确源位置进行无噪声振幅数据反演,并计算反演误差。由P波和S波振幅通过MTI和STI获得震源矩张量,反演分别采用单井(B3井)、双井(B3、B2井)和三井(B1、B2、B3井)数据。

图5 模型观测系统、合成记录及沙滩球
(a)震源点和观测井的位置; (b)包含水平层的模型,B1、B2和B3为垂直井,井中布置了检波器,VP上=4400m/s,VS上=2400m/s,VP下=4200m/s,VS下=2200m/s,红线为直达波路径,蓝线为反射波路径; (c)震源机制Hudson分布图,Φ=40°,δ=60°,θ=-30°,α=15°; (d)由格林函数合成的P波数据; (e)由格林函数合成的S波数据; (f)真实震源机制沙滩球; (g)单井STI反演沙滩球; (h)三井STI反演沙滩球
固定其他角度,改变张裂角,利用精确介质模型和精确源位置反演,反演时联合使用了P波和S波的振幅。研究表明,采用STI时,双井和三井都能获得较好的张裂角反演结果。图6为无噪条件下联合使用P波和S波振幅的单井、双井、三井STI和MTI结果及MCLVD、MDC绝对误差。由图可见:单井MTI(图6a左)造成MDC(图6a右)和MCLVD(图6a中)的较大误差,STI(图6a左)的MCLVD(图6a中)和MDC(图6a右)在α较小时存在误差,其他角度反演效果较好;双井STI(图6b左)效果较好,而矩张量反演存在误差(图6b中、图6b右);三井MTI和STI的反演效果较好(图6c)。
随机产生200个不同类型的震源机制,反演时联合使用了P波和S波振幅。图7为无噪条件下联合使用P波和S波振幅的反演结果Hudson分布。由图可见,单井STI存在一定误差(图7a),单井MTI结果不合理(图7b),三井STI(图7c)和MTI(图7d)的结果较合理。由于STI采用非线性反演算法,当满足迭代终止条件时(如误差达到规定要求或达到最大迭代次数)终止迭代并给出结果,所以部分结果存在一定误差。
针对随机产生的200个震源机制,图8为无噪条件下三井单独使用P波或S波振幅的反演结果Hudson分布。由图可见,三井P波STI存在略微误差,整体反演效果较好(图8a),三井P波MTI的结果合理(图8b),三井S波STI结果存在个别误差(图8c),三井S波MTI的结果不合理(图8d)。因此,三井的P波STI、S波STI、P波MTI的效果较好,S波MTI无法获得合理的结果。
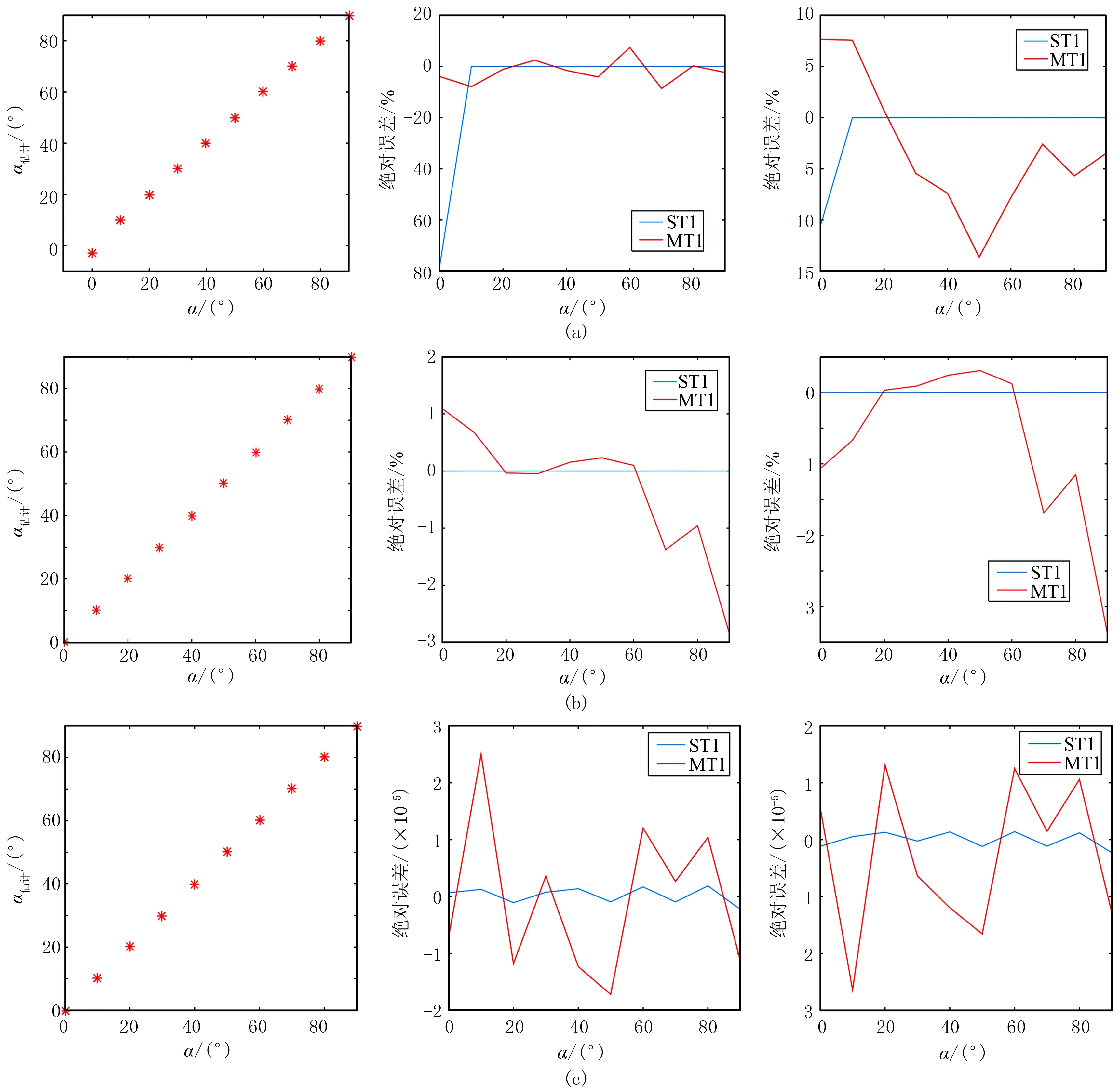
图6 无噪条件下联合使用P波和S波振幅的单井(a)、双井(b)、三井(c)STI和MTI结果(左)及MCLVD(中)、MDC(右)绝对误差

图7 无噪条件下联合使用P波和S波振幅的反演结果Hudson分布

图8 无噪条件下三井单独使用P波或S波振幅的反演结果Hudson分布
2.3 基于含噪振幅数据的反演
图9为含噪条件下联合使用P波和S波振幅的单井、双井、三井STI和MTI结果及MCLVD、MDC绝对误差。由图可见:双井和三井STI抗噪性较好,能获得较好的α反演结果(图9b左、图9c左);当α较小时单井反演的MCLVD(图9a中)和MDC(图9a右)误差较大,其他角度反演结果较好。因此,含噪时单、双井和三井的MTI精度不高。
对观测数据添加不同的随机噪声进行100次反演时联合使用了P波和S波振幅,震源机制采用图5c。图10为含噪条件下联合使用P波和S波振幅的反演结果Hudson分布。由图可见,单井STI结果较合理(图10a),单井MTI结果不合理(图10b),三井STI的结果接近单井STI(图10c),三井MTI结果较合理,但分布较散(图10d)。因此,单井STI的效果较好,单井MTI的结果不合理,三井STI和MTI的效果较好。综上所述,STI抗噪性更好,反演结果分布更集中,MTI的结果相对较分散。
图11为含噪条件下三井单独使用P波或S波振幅的反演结果Hudson分布。由图可见,三井P波STI(图11a)、S波STI(图11c)的结果接近真实源,P波MTI(图11b)的结果在真实源附近分散,反演结果较合理, 三井S波MTI的结果不合理(图11d)。因此,三井P波或S波STI的效果较好,S波MTI结果的误差较大,P波MTI的效果也较好,但是结果相对分散。

图9 含噪条件下联合使用P波和S波振幅的单井(a)、双井(b)、三井(c)STI和MTI结果(左)及MCLVD(中)、MDC(右)绝对误差
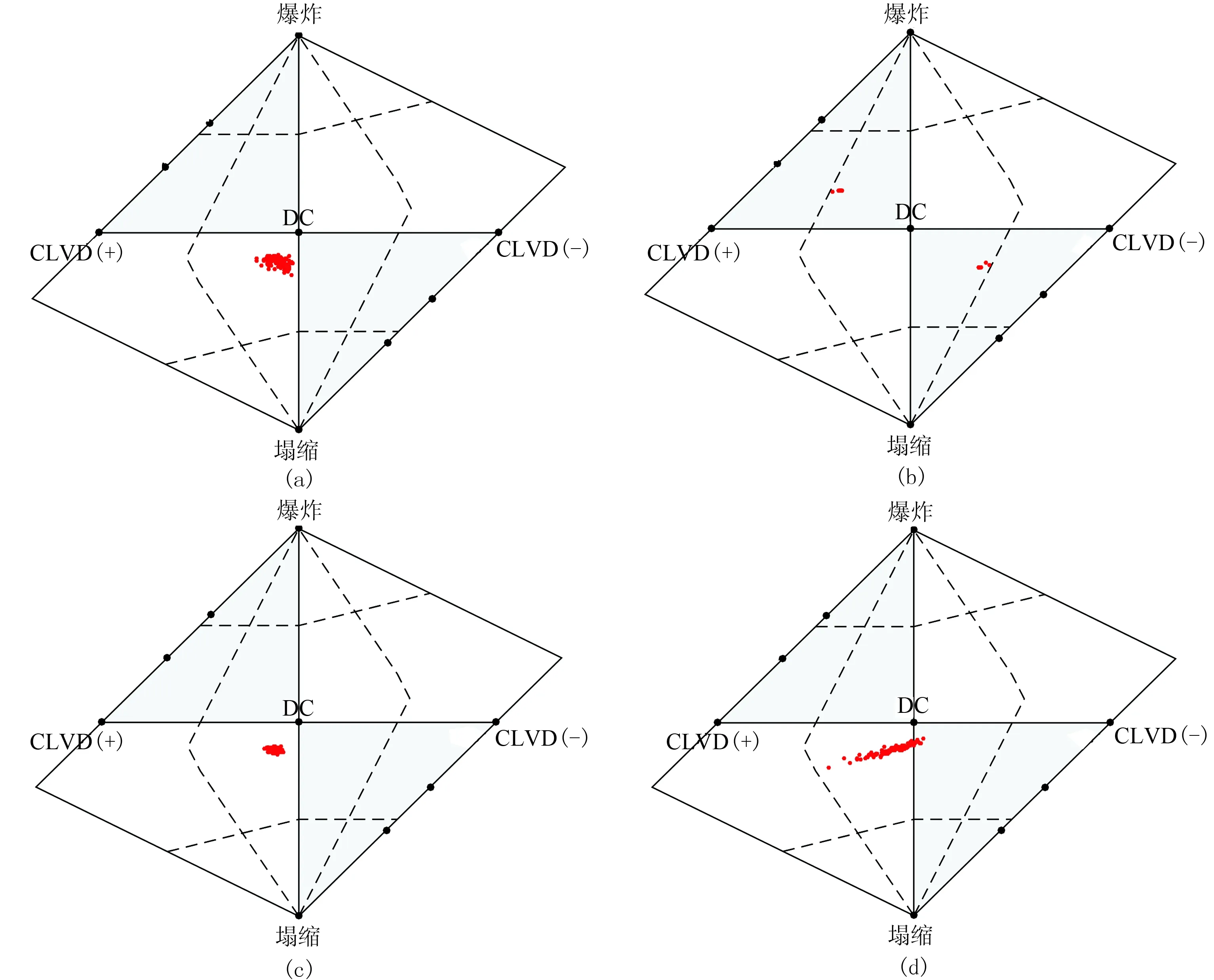
图10 含噪条件下联合使用P波和S波振幅的反演结果Hudson分布

图11 含噪条件下三井单独使用P波或S波振幅的反演结果Hudson分布
3 结论
本文研究了基于剪张源约束的微地震震源机制解反演原理,通过理论模型记录测试、分析了方法的应用效果。将矩张量限制为描述剪张源模式,采用非线性反演算法,相对矩张量模型空间参数较少,反演效果较好。
(1)无噪观测数据在不同张裂角的反演结果表明,矩张量和剪张源约束三井反演结果明显好于单井,在井数据较少时剪张源约束反演效果更好。
(2)含噪观测数据在不同张裂角的反演结果表明:矩张量和剪张源约束三井反演误差均小于单井;剪张源约束反演的抗噪性更好,在井数据较少时也可获得较好的反演效果。
(3)单井P波和S波联合振幅矩张量反演和三井S波矩张量振幅反演都会出现很大的误差, P波和S波联合振幅剪张源反演或单独P波、S波振幅剪张源反演都能获得较好的效果,即剪张源反演的振幅数据选择性更大。
