基于Gaussian-LM 算法的便携式多道γ 能谱仪自动稳谱研究

段金松， 李 婷， 王 玮， 麻金龙， 武旭东

（核工业北京地质研究院， 北京 100029）

地面γ 能谱测量作为目标区域放射性矿产勘查的一项重要技术手段， 其测量稳定性与准确度受到谱线漂移的影响， 而引起谱漂的主要因素为温度变化［1］。 由于便携式多道γ能谱仪的探测器设计多采用闪烁体与光电倍增管组合的形式， 该组合测量方式的温度效应明显［2］。 闪烁体发光效率、 发光衰减时间等指标随温度变化而变化； 光电倍增管暗电流脉冲、 灵敏度等基本特性受温度影响； 此外，其外围电路系统也具有一定的温度系数。 这些因素共同导致探测器输出信号幅度改变、能量峰位漂移， 对能谱数据的解析造成困难。因此， 自动稳谱算法或稳谱系统的设计与研究是十分必要的。

常见的稳谱措施为采用放射源作为参考源的稳谱方法， 即在探测器内嵌一个低能γ射线参考源或α 射线参考源， 通过稳定该参考源的等效峰位达到稳定待测能区谱峰的目的［3-4］。 由于参考源形成的参考峰在低能区，当环境温度差异较大时， 谱漂的非线性导致稳谱效果并不理想。 采用单色LED 作为外部光源形成参考峰成为代替上述内嵌放射源稳谱的一个新的方案， 系统根据测量得到的峰位道址变化信息， 通过调整能谱仪的程控放大器及数控高压进行反馈控制， 使LED 参考峰位稳定不变， 从而达到稳定被测特征峰的目的［5-6］。 但该方法只能校准光电倍增管及外围电路的温漂影响， 缺少对闪烁体温度效应的有效补偿。 目前关于使用测量能谱数据拟合寻峰， 识别放射性核素并进行稳谱的方法已有研究［7-8］。 但对于放射性物质含量较低的测量对象， 稳谱时间可能过长， 对测量结果造成误差。 笔者使用Gaussian-LM 算法进行拟合寻峰， 通过PID 动态调节的方式实现系统快速自动稳谱， 为野外地面γ 能谱准确测量提供技术支撑。

1 特征峰稳谱原理

图1 特征峰自动稳谱流程图Fig. 1 Flow chart of spectral auto stabilization

天然放射性环境测量过程中， 在待测能谱中总能找到K、 U、 Th 中的一个特征峰用作系统自动稳谱， 其工作原理如图1 所示。 系统通过多道数据采集卡对全谱数据进行采集，依据行业标准EJ/T 584—2014 《勘查用便携式γ 辐射仪和四道γ 能谱仪》 设置能量开窗范围分别为 K： 1.37～1.56 MeV， U： 1.66～1.88 MeV， Th： 2.42～2.79 MeV。 当任一核素能窗范围内累计计数满足既定阈值时， 进行数据拟合并寻峰求得当前核素的特征峰位。 比较实测峰位与理论峰位的偏差计算当前谱漂移量， 并设置相应的高压控制值。 系统通过PID控制算法实时调节高压模块增益， 实现测量周期内实测特征峰在标准道址附近很小的区间内波动， 达到稳谱的目的。

2 拟合寻峰方法

2.1 Gaussian 函数

由于放射性统计涨落、 闪烁体发光效率的不均匀性及仪器固有的涨落特性， 使闪烁探测器的输出脉冲幅度围绕某均值小幅涨落，故 γ 能谱单能峰近似服从高斯分布［9-10］， 如式（1）所示。

式中： 变量x—γ 射线能量或能谱曲线道址；h—峰高； μ—标准峰位对应的能量或道址； σ与半峰宽的关系—FWHM＝2.355 σ。 通过求h、 μ 和 σ 可有效确定特征峰面积、 峰位及其边界值。 经试验验证， 通常选择 μ±2.58 σ 的置信区间， 即置信概率大于99.0%来确定特征峰边界较为合适。

2.2 LM 算法对参数寻优

Levenberg-Marquart 算法 （简称 LM 算法）是基于高斯－牛顿法和梯度下降法提出的参数向量最优化算法［11］， 本质是用模型函数对待估参数在其临域内做线性近似。 它在高斯－牛顿法基础上引入阻尼因子控制每一步迭代的步长以及方向， 通过自适应调整阻尼因子实现收敛， 使模型未知参数不断逼近真值， 在进行能谱数据拟合优化过程中得到稳定的结果。 迭代初期， 首先需要根据能窗范围内谱数据预估参数初始值。 该初始值的选取是决定算法迭代速度和计算精度的关键因素， 选取的初值越接近真实值， 收敛和求解全局最优解的速度越快。

LM 算法具体实现流程如图2 所示， 初始化参数（h、 μ、 σ）及阻尼因子 λ， 计算当前参数值处的残差向量与Jacobian 矩阵， 根据阻尼因子及 Jacobian 矩阵获取 Hessian 矩阵及迭代步长， 由迭代步长计算新的可能的待估参数， 进而获取新的残差向量， 对比残差决定参数及阻尼因子的更新方向。 在曲线拟合实践中， 依条件选用不同的调整系数α、 β 实现参数的快速收敛， α 称为正向调整系数通常选取0.1， β 称为逆向调整系数通常选取 10。 λ′＝α λ 或＝β λ， 其中 λ′表示调整后的阻尼因子。

3 系统实时稳谱

为了实现系统快速稳谱， 防止在校正谱漂的过程中出现高压增益调节不足或过调节的现象， 根据上述寻峰结果， 结合系统控制原理， 采用软件数字PID 控制算法进行稳谱处理， 通过对高压增益调节曲线分析， 制定优化模糊规则， 并将模糊规则参数代入PID实际计算模型中， 增强系统鲁棒性， 其工作原理如图3 所示。

系统以目标高压控制量D 作为PID 输出控制量， 选取拟合峰位对应的道址P 作为自变量， 对于单一控制变量， PID 控制算法为：

图2 LM 算法实现流程Fig. 2 Levenberg-Marquart algorithm implementation process

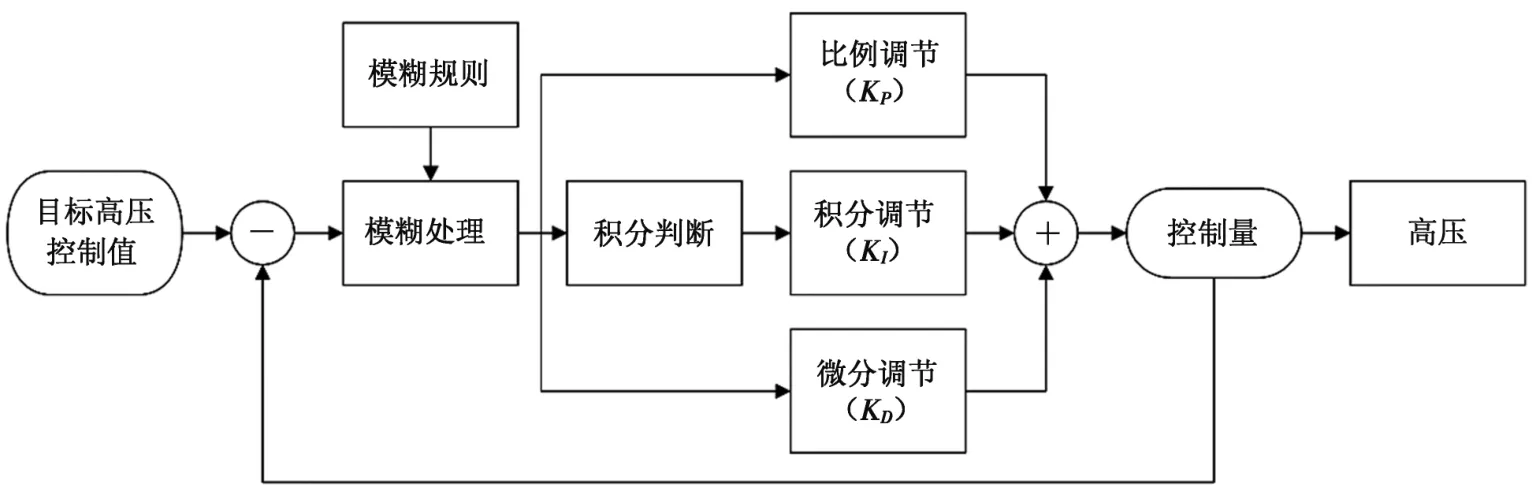
图3 PID 控制算法Fig. 3 PID control algorithm

式中： Pref—理论峰位对应道址； Pn、 Pn-1、 Pn-2—第 n 次、 第 n-1 次、 第 n-2 次得到的拟合峰位道址； KP、 KI、 KD—比例单元、 积分单元和微分单元的控制因子； 其中KI的主要作用为增益控制， 增加KI可降低系统的稳态误差，提高系统响应速度。 KP和KD与峰位道址P 的变化率相关， 能够预测偏差， 产生超前的校正作用， 较好地改善动态性能［12］。

4 试验结果及讨论

4.1 拟合寻峰结果

选用钾、 铀、 钍单一核素模型针对能窗划分范围内的特征峰进行拟合， 采用LM 算法对Gaussian 拟合函数进行参数寻优， 结果如图4 所示， 分别求得不同核素模型的拟合峰位、 半峰全宽（FWHM）如表 1 所示。

图4 Gaussian 拟合及LM 算法寻优结果Fig. 4 Gaussian fitting result and Levenberg-Marquart algorithm optimization

由表1 可知， 采用LM 算法对特征峰进行拟合取得较好效果，R2（确定系数）均大于0.95，其拟合峰位道址与理论峰位较接近， 针对1024 道便携式多道 γ 能谱仪， 误差在±1 道。因此， 在仪器自动稳谱过程中可以使用该算法进行特征峰寻峰操作。

4.2 稳谱效果

将便携式多道γ 能谱仪置于可编程温湿度环境实验箱 （型号： CTH-WK4503-02FO）中， 开展一系列环境温度渐变试验， 考察基于Gaussian 与LM 算法的特征峰自动稳谱效果。 试验温度范围设置为-20～50 ℃， 实验箱以 3 ℃/min 的速率按照 20→-20→50 ℃的顺序进行降温和升温操作。 分别选用钾、 铀、 钍单一核素模型， 以及环境本底模拟多种γ 能谱仪自动稳谱环境， 设置单次谱数据采集时间为60 s， 实时稳谱效果如图5 所示。

图5 中红色线为特征峰位， 黑色线为高压值。图5a 中， 环境本底情况下， K 的特征峰（能量为 1.46 MeV） 较明显， 故采用 K 峰进行稳谱。 由图5 可知， 随着环境温度变化， 仪器可以实现自动高压补偿并确保特征峰在很小的范围内波动。

表1 拟合寻峰结果分析Table 1 Finding result Analysis of peak fitting

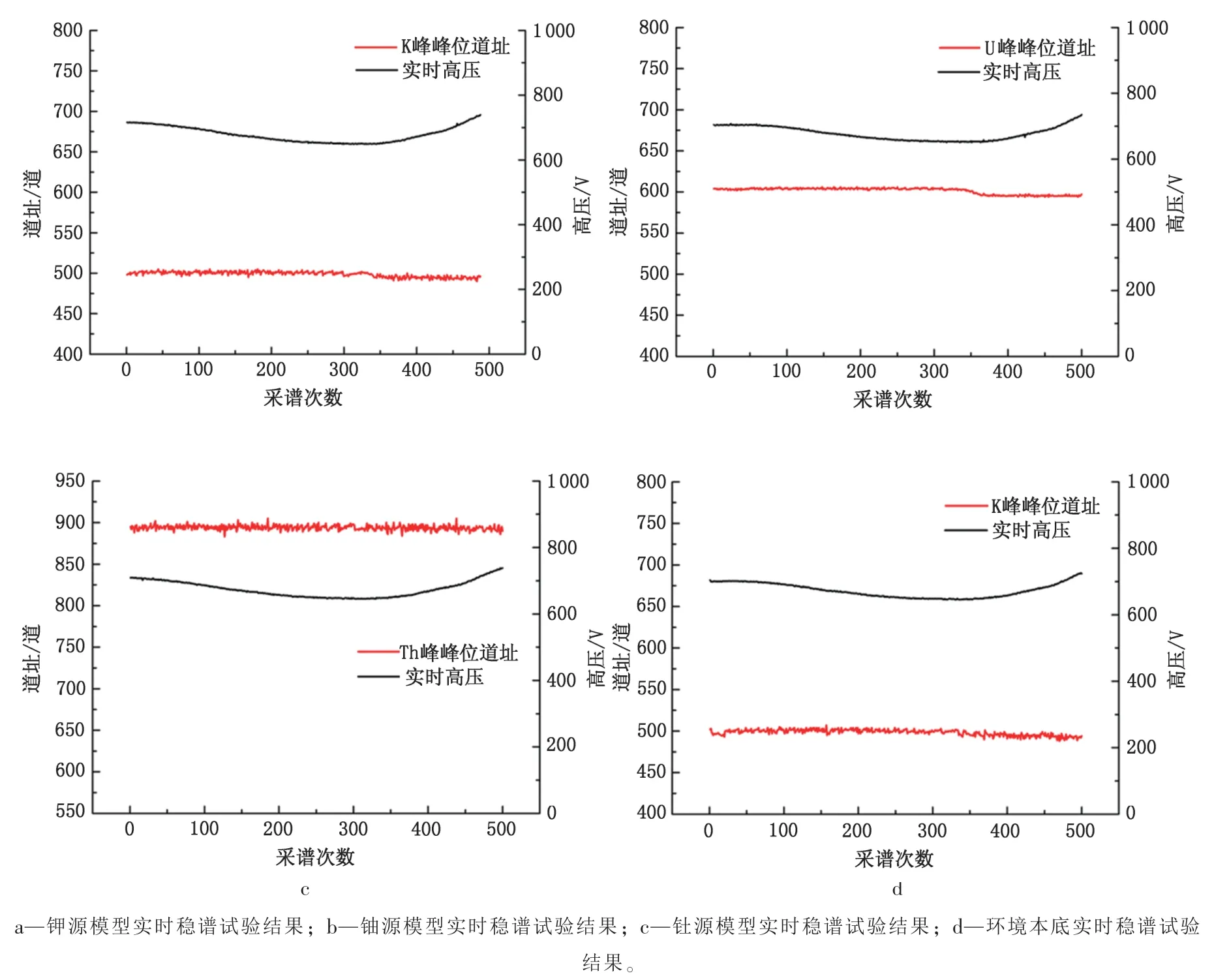
图5 便携式多道γ 能谱仪稳谱验证试验Fig. 5 Verification experiment of spectral stabilization for portable multi-channel gamma spectrometer

基于上述仪器实时稳谱功能， 选择混合模型， 从-20～50 ℃， 以 10 ℃的温度间隔分别设置8 个温度梯度， 到温后保持2 h 进行谱数据采集， 验证不同温度梯度下拟合寻峰，自动稳谱精度， 结果如表2 所示。

由表2 可知， 不同温度梯度下， 开启自动稳谱功能后的实测峰位道址最大谱漂不超过±3 道， 该结果表明了Gaussian 拟合函数与LM 算法参数寻优在自动稳谱过程中的可靠性， 以及上述通过PID 进行高压模块增益调节在实时稳谱中的可行性。 但本文介绍的自动稳谱算法对于重合峰分辨能力较弱， 下阶段可采用多阶Gaussian 函数拟合， 增强重峰分辨能力。

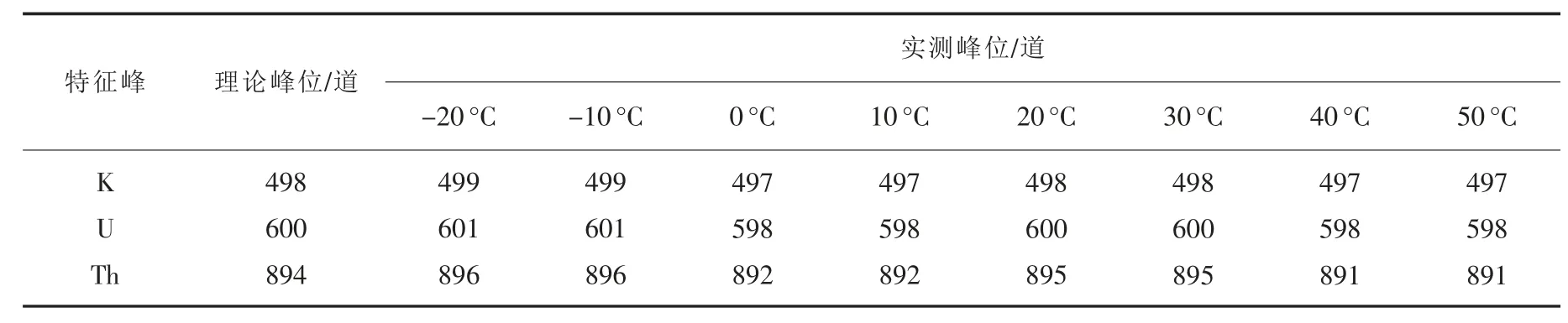
表2 不同温度梯度下的特征峰稳谱效果Table 2 Effect of spectral stabilization under different temperature gradients

5 结语

针对便携式多道γ 能谱仪测量过程中因温度影响造成谱线漂移的问题， 提出采用LM算法利用逐次逼近原理对Gaussian 拟合函数进行参数寻优， 获取当前特征峰峰位道址，通过峰位偏差计算当前谱漂移量， 再依据谱漂移量利用PID 控制算法调节高压控制字继而进行相应的高压补偿， 实现系统自动稳谱功能， 该方法具有硬件资源少、 响应速度快、数据运算量小等优点， 很适合便携式仪器。经试验验证， 在-20～50 ℃范围内实测峰位道址最大谱漂为±3 道。 目前该方法已应用于γ能谱仪实际测量中， 运行稳定， 结果可靠，达到预期要求。