半Bent函数和多输出布尔函数的构造*
2020-03-02郭梦飞孙玉娟李路阳
郭梦飞, 孙玉娟, 李路阳
1.西安电子科技大学综合业务网理论及关键技术国家重点实验室, 西安710071
2.密码科学技术国家重点实验室, 北京100878
3.西安邮电大学通信与信息工程学院, 西安710121
1 引言
Bent 函数的概念由 Rothaus 于 1976 年提出[1], 它是非线性度最高的布尔函数, 具有最好的抗线性攻击的能力.遗憾是它不具有平衡性, 不能直接应用于密码系统中, 因此构造具有高非线性度的平衡函数是密码函数设计中重要的研究方向之一.半bent 函数的概念在 1994 年的亚密会上被提出[2], 它是非线性度最优的 Plateaued 函数 (三谱值函数)[3], 这类函数可以是平衡的, 可以具有偶数个变元, 也可以具有奇数个变元和偶数元.对于变元个数n 为奇数的半bent 函数可用于构造具有低互相关值的序列簇, 该序列被称为Gold[4], 并且这种序列在密码学和码分多址(CDMA) 通信系统中具有广泛的应用.在Gold 的开创性工作之后, 许多研究者致力于寻找新的半 bent 序列家族.近些年来已经有了很多关于半 bent 函数的研究, 2004 年 Carlet 在 [5]中对布尔函数的二次构造进行研究, 并利用 bent 函数与半 bent 函数的间接和构造了新的半 bent 函数.2005 年 Charpin 和 Pasalic 从有限域上直接构造了二次半 bent 函数[6].2009 年 Sun 和 Wu 给出了变元为偶数的一些具体的二次半 bent 构造和二级半 bent 构造[7].2011 年 Mesnager 证明了零和二元 Kloosterman 和的四个值可以在偶数维变元上构造半 bent 函数[8].2018 年Xie 和Luo 在[9]中, 从有限域上的利用多项式给出了二次半bent 函数的新构造结构.在现有的关于半 bent 函数构造的参考文献中, 大部分都是从有限域上利用迹函数和幂函数导出半 bent 函数且变元个数是偶数, 也有很多利用已知函数进行二次构造而得.当变元为奇数时, 通过直接构造半bent 函数的方法很少.本文从向量空间的角度出发, 利用向量空间上的不相交线性码直接构造了一类变元个数为奇数的半 bent 函数, 其构造思路来自 PS 类 bent 函数[10].该构造方式实现简单, 只需得到不相交线性码和其对偶码的生成矩阵便能给出函数的表达式, 并且可以快速的计算出函数真值.
此外, 多输出布尔函数 (向量值函数) 在特定的流密码系统中使用, 可以使密钥流的生成速率大大提高, 因此其实际中的应用更多.目前关于多输出函数的构造大部分都是从有限域上开展, 在向量空间上利用不相交线性码构造多输出布尔函数文献很少, 见文献[11,12], 并且这些文献中多输出布尔函数的输出维数最大只能达到输入维数的一半, 且输入变元维数必须是偶数.本文将利用不相交线性码构造一类具有高非线性度平衡的 (n, n −k) 多输出布尔函数, 其中n/3 < k < n/2, 保证了在一定的非线性度条件下, 其输出维数大于输入维数的一半, 且输入变元的维数可以为奇数也可以为偶数.
本文内容安排: 第 1 节介绍了构造背景及主要构造的基本思想.第 2 节主要介绍了布尔函数和线性码部分的基础知识.第 3 节主要是具体的半 bent 函数构造和证明, 以及多输出布尔函数的构造和证明.第4 节则是对本文工作的总结和下一步工作展望.
2 基础知识
定义 1设 Xn∈, 函数 f(Xn) 是从到 F2的映射, 则函数 f(Xn) 就是一个 n 元布尔函数.
一般来说, 布尔函数具有多种表达方式, 如真值表、序列、代数正规型、矩阵等方法.其中最常用的是代数正规型表示:
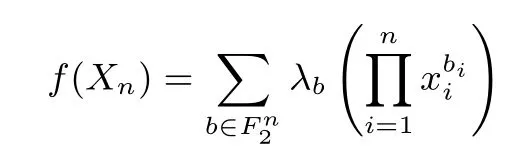
其中, 代数正规型中各项的系数 λb∈ F2, 且 b=(b1,··· ,bn)∈.
令 Bn表示所有 n 元布尔函数的集合, f(Xn) ∈Bn.设函数的自变量 Xn= (x1,x2,··· ,xn) ∈,常数向量 α =(α1,α2,··· ,αn)∈, 这两个向量的内积的定义如下:
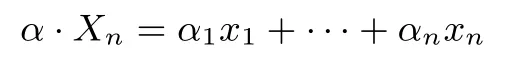
则布尔函数f 在α 点处的Walsh 谱的计算公式为:
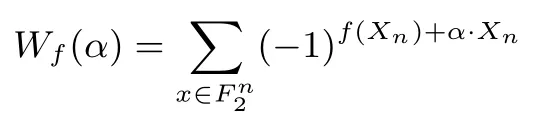
定义 #supp(f)={Xn|f(Xn)=1, Xn∈} 为 f 的支撑集, #supp(f) 指的是 f 的汉明重量, 一个 n 元的函数 f 是平衡函数当且仅当 #supp(f) = 2n−1, 或是 Wf(0n) = 0.这里 0n表示 n 长的 0 向量.
定义 2一个 n 元的布尔函数 f 被称为半bent 函数, 当且仅当对任意 α ∈

定义 3一个n 元的布尔函数f 的非线性度表示为Nf, 衡量了函数f 到所有仿射函数的最小距离,

其中A(n) 表示所有n 元仿射函数的集合, l 表示集合A(n) 中任意一个仿射函数.经过推导, 得出Nf的计算公式为:
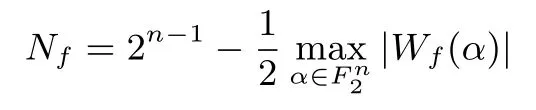
根据 Parseval 恒等式[13],

所以任意一个布尔函数f 的非线性度Nf都满足:

定义 4(n,m) 多输出布尔函数 F =(f1,··· ,fm) 的非线性度 NF定义为
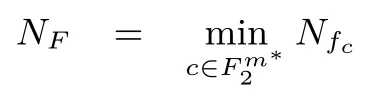
其中 fi∈ Bn, c=(c1,··· ,cm) ∈, 即

定义 5对于一个 [n,m]线性码的集合 C = {C0,C1,··· ,CN−1}, 如果 0 ≤ i < j ≤ N −1, 线性码集合C 满足条件
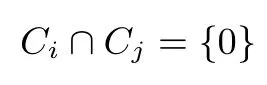
设 S 和 T 是线性空间 V 的子空间, 称所有能表示成 x+y, 而 x ∈S, y ∈T 的向量组成的子集为 S与 T 之和, 并记为 S+T.且它们的和 S+T 也是V 的子空间.
引理 1[14](维数公式) 设S 和T 是线性空间V 的两个子空间, 则

其中dim S 表示线性空间S 的维数.
3 主要构造
3.1 n为奇数时 [n,k]不相交线性码的构造
本节将设计新的不相交线性码, 为半bent 函数的构造作铺垫.文献[15]给出了一种不相交线性码划分方式.参考这篇文章, 当n 为奇数时, 可以将按照下述方式进行划分.
构造 1设n=2k+1,令中任意元素都可以写成(x,y).如果α 表示有限域 F2k+1中的一个本原元, 则 (1,α,··· ,αk) 就是有限域 F2k+1中的一组基.定义一个双射 π : F2k+1→则 π 的映射关系可以表示为:
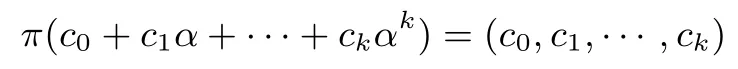
令 Gi(0 ≤ i ≤ 2k+1−2) 是 [n, k]生成矩阵, 其表达形式为

G2k+1−1是 [n,k]生成矩阵, 其表达形式为

G2k+1是 [n,k+1]生成矩阵, 其表达形式为

定理 1设 n 为奇数, n = 2k+1.则上述构造的 Gi(0 ≤ i ≤2k+1) 生成的空间 Ei组成一个不相交码集, 且划分
证明:令 E0,E1,··· ,E2k+1−1, E2k+1是由上述生成矩阵生成的码空间.
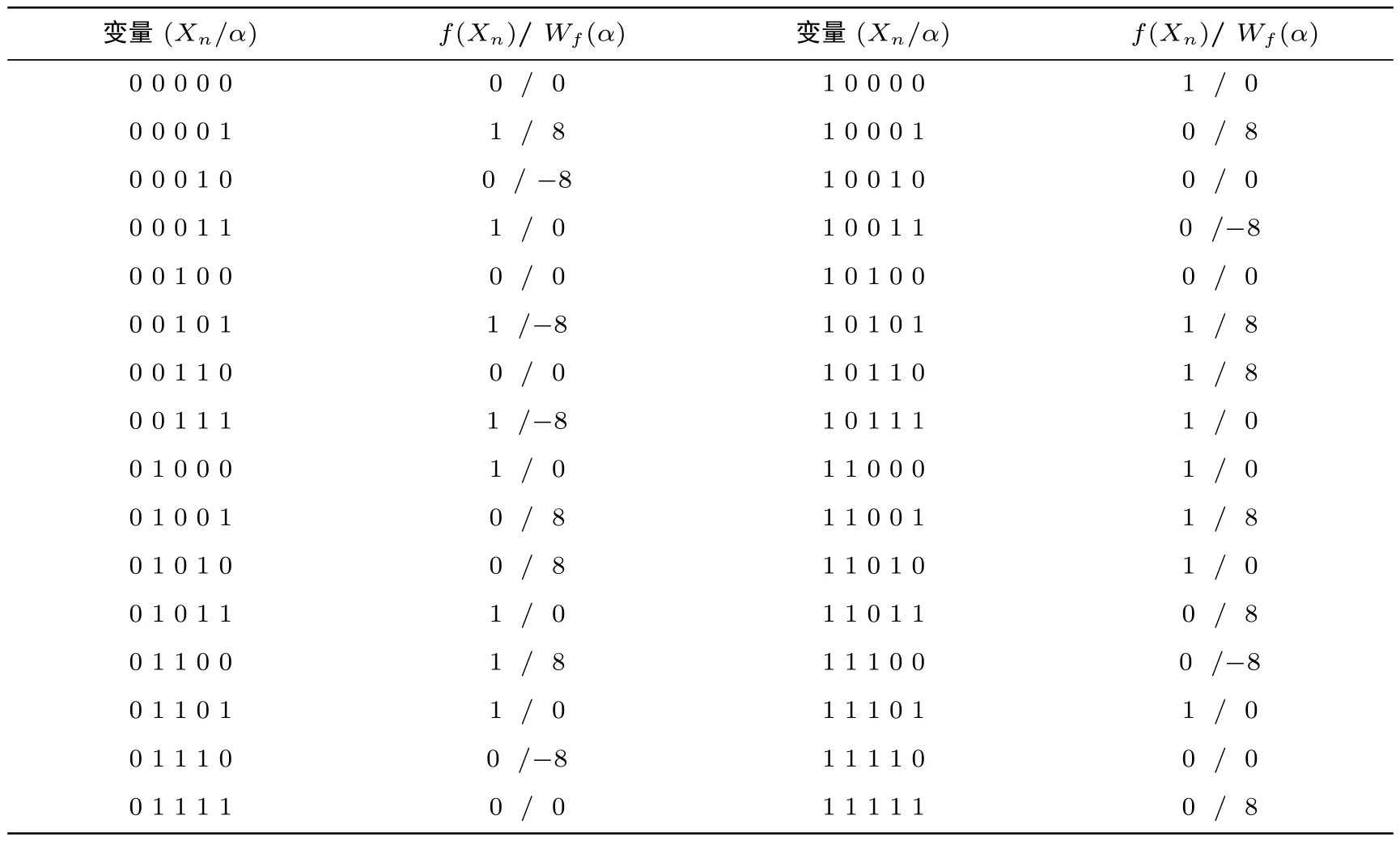
(1) 当 0 ≤ i < j ≤ 2k+1−2 时, 此时 Gi, Gj的前 k 位是一个单位阵, 后 k+1 位是一个由 F2k+1中本原元表示 k 个线性无关向量, 对任意 0 ≤i (2) 当 0 ≤ i ≤ 2k+1− 2, 2k+1− 1 ≤ j ≤ 2k+1时, 则 Gj的前 k 位或者后 k+1 位是全 0 矩阵, 显然 Ei∩Ej={0}; (3) 当 2k+1− 1 ≤ i < j ≤ 2k+1时, Gj前 k 部分为 0 矩阵, Gi后 k+1 部分为 0 矩阵, 所以Ei∩Ej={0}, 且互相对偶, 因此上述构造组成一个不相交码集. 令n=2k+1, 可以利用上述构造1 中的不相交码构造一类新的半bent 函数. 构造 2设 E0,E1,··· ,E2k+1是由上述生成矩阵 G0,G1,··· ,G2k+1生成的码空间, 所以对任意 0 ≤i 定理 2设f(Xn) 是构造 2 所构造的函数, 则函数 f(Xn) 是一个半 bent 函数. 证明:令是上述不相交码的对偶空间, 则对任意 (3) ω ·Xk+1是一个线性函数, 且当 αk+1= ω 时, 必有 α ∈ S.因为 αk+1= ω 的 α 取值共有2k个, 且每个 α 都会出现在2 个不同的所以上述定义的集合 (4) 下面来计算函数f 的谱值 又 αk+1·Xk+1≡ 0, 则 所以 Wf(α)=U1+U2+U3=0. i.若 α 的后 k+1 位等于 ω 时, 有 U1=2k, U2= −2k, U3=2k+1, 所以 Wf(α)=2k+1. ii.若 α 的后 k + 1 位不等于 ω, 有 U1+ U2∈ {0,±2k+1}, U3= 0, 所以 Wf(α) ∈{0,±2k+1}. 综上 Wf(α) ∈ {0,±2k+1}, Nf= 2n−1− 2k+1−1= 2n−1− 2(n−1)/2, 所以 f(Xn) 是一个半 bent 函数. 下面将给出一个例子, 对构造2 进行更详细的阐述和解释. 例 1设 n=5, k =2.选择有限域 F23上的一个本原多项式 h(x)=x3+x+1, 令 β 是本原多项式的一个根, 则可以将划分为23+1 个不相交码空间, 及其对偶空间生成矩阵如下 则B ={0,1,2,3,4,5,6,7}, B1={1,2,4,7}, B2={0,3,5,6}. 因此可以得出上述构造的函数f 的真值表, 同时根据真值表易得出f 的谱值分布.见表1. 表1 f 的真值表和谱值分布Table 1 Truth table and Walsh spectra of f 根据表1 易验证 (1) 若 α 的后 3 位等于 ω 时, Wf(α)=23. (2) 若 α 的后 3 位不等于 ω, Wf(α)∈ {0,±23}. 综上 Wf(α) ∈ {0,±23}, Nf=25−1− 23−1=12.所以 f 是一个半 bent 函数. 注1对上述构造和证明, 需要做出以下几点说明. i 公式(2) 中集合B1是选取下标小的对偶码的下标集; 公式(3) 中集合B2是选取下标大的对偶码的下标集; ii 但需要指出的是集合B1和B2不需要非要这样规定, 可以有多种选择, 只要保证当 α ∈且α ∈时, 下标i 和j 不放入同一个集合, 即不同时放入B1或B2即可. iii 所以当n=2k+1 时, 每当ω 固定时可以构造出 22k种不同的半bent 函数; 又因为ω ∈,所以一共可以构造出(2k+1−1)×22k种不同的半bent 函数. 本节将利用不相交码和高非线性度置换来构造一个(n, n −k) 多输出布尔函数, 使得在保证一定非线性度的条件下, 输出变量的个数大于输入变量的个数的一半. 构造 3令 n/3 令 Gi(0 ≤ i ≤ 2n−k− 2) 是 [n,k]生成矩阵, 其表达形式为 G2n−k−1 也是 [n,k]生成矩阵, 表达形式为 G2n−k是 [n,n − k]生成矩阵, 其表达形式为 下面开始构造(n,n −k) 出多输出函数, 且使输出维度大于等于输入长度的一半.构造方法参考文献[11,12], 令 E0,E1,··· ,E2n−k是上述生成矩阵的生成空间, 设定义一个映射 显然 φ(y)∈ {0,1,2,··· ,2n−k− 1}.对任意的上的置换函数 H(y)=(h1(y),h2(y),··· ,hn−k(y)),定义{0,1,2,··· ,2n−k−1} 的子集Ai和其补集如下 易得Ai和的大小满足|Ai|=2n−k−1.令G(Xn−k)=(g1(Xn−k),g2(Xn−k),··· ,gn−k(Xn−k)) 为一个 (n − k,n − k) 置换, 其中 Xn−k=(xk+1,xk+2,··· ,xn).F(Xn)=(f1(Xn),f2(Xn),··· ,fn−k(Xn)),其中分量函数为 定理 3设F(Xn) 是构造 3 所构造的函数, 则函数F(Xn) 是一个 (n, n −k) 平衡的多输出函数, 其输出维度大于等于输出的一半, 且非线性度满足NF≥2n−1−2n−k+NG. 证明:令则 F(Xn) = (f1(Xn),f2(Xn),··· ,fn−k(Xn)), 其分量函数的非零线性组合可表示为 根据置换函数的性质, c1h1⊕ ···⊕cn−khn−k(y) 总是平衡的, 所以的 walsh 谱值为: (1) 平衡性: 当 α=0n时, 显然 U =0; 又 gc是一个线性函数, 有 Wgc(0n)=0, 所以 Wfc(0n)=0,即F 是一个平衡函数. (2) 输出维数: 由于 n/3 (3) 非线性度: 因为 max|U|=2k× 2n−k−k=2n−k, 代入得式 (4) 本文中, 首先基于不相交线性码构造了一类新的半 bent 函数; 其次又利用不相交线性码和高非线性度置换函数构造了多输出的布尔函数, 并使其输出维数大于输入维数的一半.本文构造的半 bent 函数相较于现有的半 bent 函数是完全不同的, 首次在向量空间上利用不相交线性码直接构造了奇数变元下的半 bent 函数, 并且其构造方法简单易于实现.相较于文献 [12], 本文构造的多输出平衡布尔函数的输出维数大于输入维数的一半且变元维数可奇可偶.但还有一些工作下一步需要解决, 怎么把本文中构造的单输出半bent 扩展为多输出半bent 函数? 当0 ≤k ≤n/3 时,怎么构造(n, n−k)的多输出布尔函数?3.2 半bent函数构造

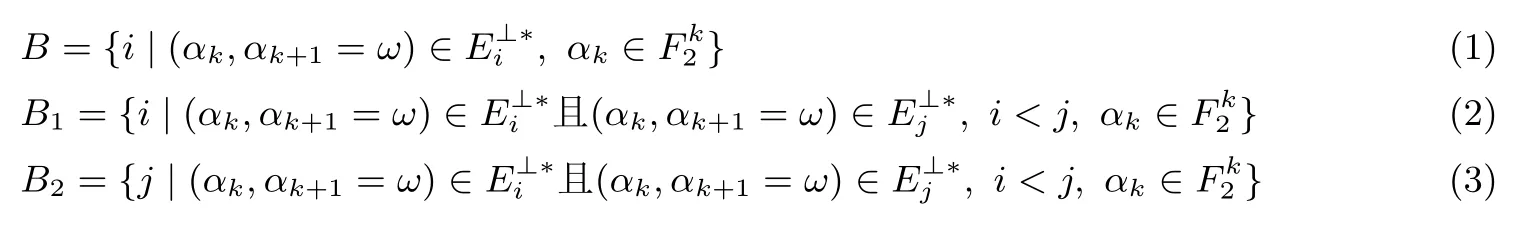


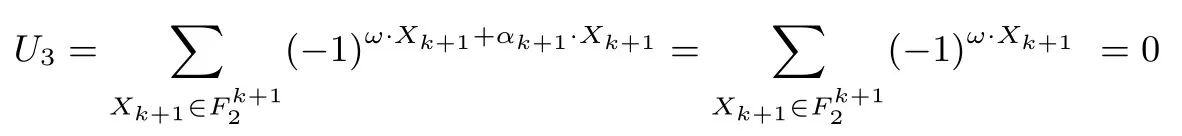


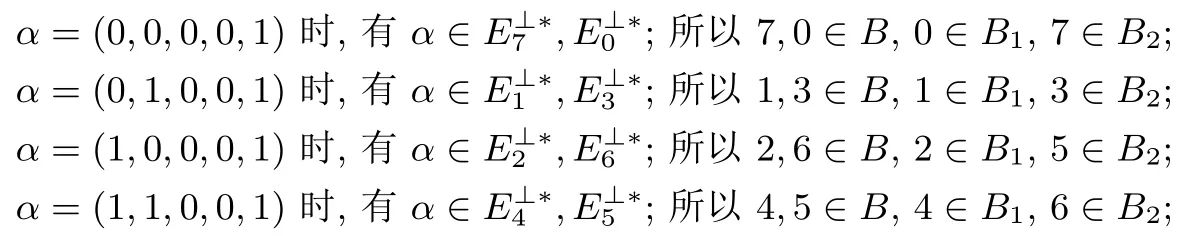


3.3 (n, n −k)多输出布尔函数的构造
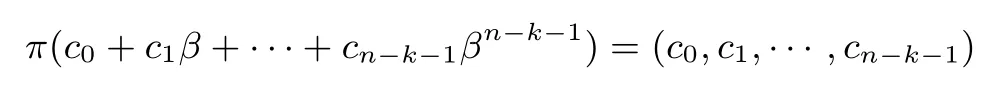
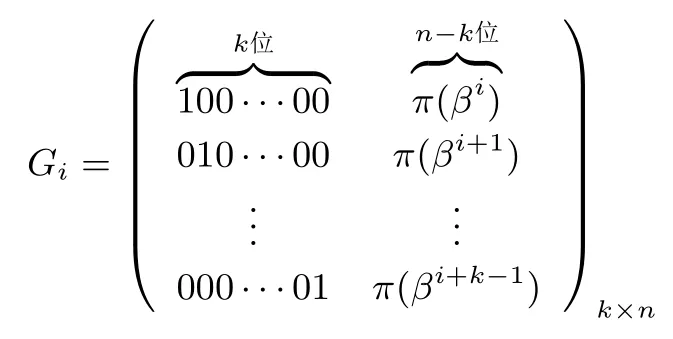


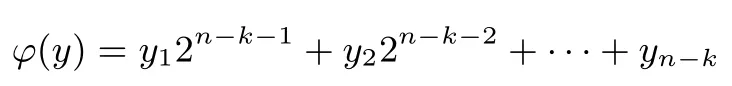


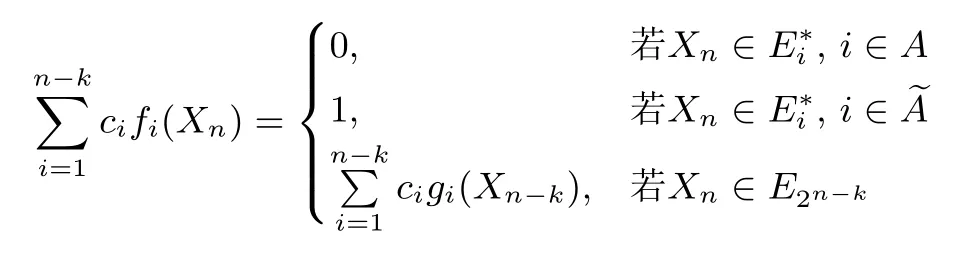


4 总结
