可变可视密码*
2020-03-02乔明秋赵振洲
乔明秋, 赵振洲
北京政法职业学院信息技术系, 北京102628
1 可视密码概述
可视密码[1]是一种秘密共享方法, 它将一个秘密图像加密成 n 个分存图像, 解密时只需 k′(k′≥ k)个分存图像叠加, 秘密图像就会呈现, 而少于 k 个分存图像将无法解密, 且不能分析出秘密图像的一点信息, Droste[2]提出了可视密码新的研究成果.目前, 已经提出了许多可视密码技术的拓展形式, 如像素不扩展型[3–7]、基于分块字典的可视密码[8,9]、基于栅格的可视密码[10,11]、没有形变的可视密码[12]、防欺骗可视密码[13]、基于三维立体分享图像的可视密码[14]、多级别的可视密码[15]等.
传统的可视密码都是单点加密, 在加密时会产生像素扩张, 结果使分享图像比原来的加密图像大许多倍, 尤其是应用在灰度和彩色图像上, 其扩张的倍数更是惊人.Hou 提出了像素不扩展的彩色可视密码[3], 林克正等提出了基于分块字典的可视密码[8].本文提出任意个点加密的可视密码, 即可变可视密码(variable visual cryptography, VVC), 一方面它解决了传统可视密码像素扩张的问题; 另一方面它非常灵活, 能使分存图像小于、等于或大于秘密图像, 从而能有效减少存储空间, 或在存储空间和图像质量之间找到一个平衡点, 也许它的优越性远不止于此.
2 传统可视密码的数学定义
秘密图像中的每个像素都单独处理, 即单点加密, 由 n 个人共享, 每个共享由 m 个黑白子像素组成.构建一个n×m 布尔矩阵B =[Bij], 当且仅当Bij=1 时第 i 个共享者的第 j 个子像素为黑; 当且仅当Bij= 0 时第 i 个共享者的第 j 个子像素为白.当把投影片叠放在一起时, 就相当于对于每一行都做了或运算.叠放后图像的灰度值与进行或运算之后的向量V 的汉明重量H(V) 成正比.解密者利用视觉系统解释灰度值如下, 如果 H(V)≥d 该点像素为黑, 如果 H(V)≤d −αm 该点像素为白.
定义 1一个 (k,n) 可视密码体制含有两个 n×m 布尔矩阵簇 C0和 C1, 如要共享一个白像素就随机从 C0中取出一个矩阵, 如要共享一个黑像素就随机从C1中取出一个矩阵.所选的矩阵定义了n 个共享者中每一个子像素的颜色.如果下列条件满足则该方法有效:
(1) 对于C0中的任意一个矩阵 S, n 行中任意 k 行进行或运算之后的向量V 满足H(V)≤d −αm;
(2) 对于C1中的任意一个矩阵 S, n 行中任意k 行进行或运算之后的向量 V 满足H(V)≥d;
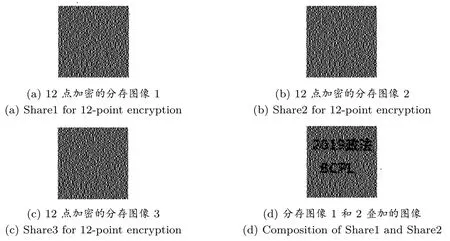
(3) 对于 {1,2,··· ,n} 中的任意一个子集 {i1,i2,··· ,iq}, q 其中: (1) m 是像素扩展度, m 越小越好; (2) α 是相对差, α 越大越好; (3) α ·m 是对比度, α ·m 越大越好; (4) 矩阵簇Ct是基础矩阵Bt进行随机列置换后所有矩阵的集合. 以(2,2) 可视密码为例, 加密基础矩阵为式(1), C0和C1分别是B0和B1进行随机列置换后所有矩阵的集合, 通过验证, 此基础矩阵满足定义的三个条件. 再有(2,4) 可视密码的基础矩阵为式(2), 也满足定义的要求. 我们不采用单点加密, 而是采用r 点加密, 加密序列长度r 可变(r >1), 那么分享图像大小就是秘密图像大小的 m/r 倍.当 r > m 时是分享图像比秘密图像小的方案; 当 r = m 时是分享图像和秘密图像一样大的方案; 当1 < r < m 时是分享图像比秘密图像大的方案 (前两种情况更具应用性).当然, r 不可能过大, 否则图像会难以识别. 对于(k,n) 可视密码, 令B0、B1分别代表对应白点与黑点的基础矩阵, 基础矩阵是m×n 矩阵, C0、C1分别是对B0、B1进行随机列置换后的矩阵集, M0∈C0, M1∈C1.加密序列长度为r, 即我们一次取秘密图像上的连续 r 个点来加密, b 代表加密序列中的黑点个数 (0 ≤b ≤r), eb则代表具有 b 个黑点的加密序列已加密过的个数, 加密程序如下: (1) 确定加密序列长度 r, 令 eb=0 for b=1,2,··· ,r; (2) 从秘密图像取出即将加密的序列, 并计算其黑点个数b; (3) if ebmod r M =M1 else M =M0 M 代表所取的加密矩阵, 将 M 的第 i 行分配给第 i 个分享者 (1 ≤i ≤n), 每个分享者拥有 m 个像素, 此m 个像素的排列方法视情况而定, 排列宗旨是使解密图像变形最小; (4) eb=eb+1; (5) 重复步骤(2)–(4) 直到秘密图像上的所有像素都加密完毕. 同传统的可视密码一样, 我们的方案也需要从对比性和安全性两个方面进行证明. 对比性:对于本方案的 (k,n) 可视密码, 若 k′(k′≥k) 个人的分享图像叠加后, 具有 b 个黑点的加密序列和具有b+1 个黑点的加密序列在叠加图像上是可区分的. 证明:B0、B1是(k,n) 可视密码的基础矩阵, 基础矩阵是m×n 矩阵, C0、C1分别是对B0、B1进行随机列置换后的矩阵集, M0∈ C0, M1∈ C1.OR(M,k′) 代表将矩阵 M 的第 i1,i2,··· ,ik′ 列进行或运算所得到的向量.E(b)代表秘密图像上具有b 个黑点的加密序列, r 代表加密序列长度. 在 r 个 E(b)加密序列中, 有 b 个使用 M ∈ C1加密, 其余的 r −b 个序列使用 M ∈ C0加密, 因此在将 k个分享图像叠加后的图像上, 在对应这 r 个区域上会有 [b×h1+(r −b)×h0]个黑点, 其中h1= H(OR(M ∈ C1,k′)),h0= H(OR(M ∈ C0,k′)),H 表示取汉明重量, 因此这 r 个 E(b)加密序列在叠加图像上的黑色程度可以表示成[b×h1+(r −b)×h0]/(r×m), 那么r 个E(b+1)加密序列在叠加图像上的黑色程度可以表示成[(b+1)×h1+(r −b −1)×h0]/(r×m).而我们知道h1和h0是可区分的,所以E(b)和E(b+1)加密序列在叠加图像的黑色程度也是可区分的. 安全性:对于本方案的 (k,n) 可视密码, 若 k′(k′< k) 个人的分享图像叠加后, 不会泄漏秘密图像的任何信息. 证明:秘密图像上的每个加密序列, 或者使用 M ∈C0加密, 或者使用 M ∈C1加密, 因为 C0和 C1满足上述安全性, 所以本方案也满足上述安全性. 以(2,3) 分享图像大小可变的可视密码为例, 图1 所示为秘密图像 (256×256), 图2 所示为 2 点加密,图3 所示为 3 点加密, 图4 所示为 4 点加密, 在图2–4 中图 (a) 是 Share1 图像, 图 (b) 是 Share2 图像, 图(c) 是 Share3 图像, 图 (d) 是图 (a) 和图 (b) 叠加后的图像.本文所有显示图像的大小是原图像的 50%. 图1 秘密图像Figure 1 Secret figure 图2 (2,3) 可视密码的 2 点加密Figure 2 2-pioints encryption for (2,3) visual cryptography 可见, 在图2 所示的2 点加密中分享图像是秘密图像的3/2, 图3 所示的3 点加密和秘密图像一样大,图4 所示的 4 点加密分享图像是秘密图像的 3/4.图2、4 所示叠加后的图像会有变形 (其实传统可视密码也产生变形). 图3 (2,3) 可视密码的 3 点加密Figure 3 3-pioints encryption for (2,3) visual cryptography 图4 (2,3) 可视密码的 4 点加密Figure 4 4-pioints encryption for (2,3) visual cryptography 若要求叠加后的图像不变形, 就应该对r 有所限制: 存在整数 p、q, 使m=p×q, 且|p −q| 最小, 那么r 可取的集合是 此例中, m=3=1×3, 即 p=1, q =3, t=1, 假设 s 取 2, 那么 r =(1×2)×(3×2)=12, 此时叠加后的图像不会变形, 且缩小至秘密图像的1/4, 如图5 所示.从图5 中可见, 对于(2,3) 可视密码, r =12时叠加后的图像不会变形. 图5 (2,3) 可视密码的 12 点加密Figure 5 12-pioints encryption for (2,3) visual cryptography 对于(2,3) 可变可视密码, 分存图像的大小、分存图像的形变程度、图像恢复效果如表1 所示, r = 2时是分存图像扩大的可视密码, 扩大为秘密图像的3/2, 有形变, 人眼辨识图像恢复效果良好; r = 3 时是像素不扩展可视密码, 无形变, 人眼辨识秘密图像恢复效果较好, 但图像个别位置边界模糊; r = 4 时是分存图像缩小的可视密码, 缩小为秘密图像的3/4, 人眼辨识图像恢复效果较好, 但边界模糊加重; r =12 时是分存图像缩小的可视密码, 缩小为秘密图像的1/4, 无形变, 人眼辨识图像恢复效果尚可, 边界模糊较重. 表1 (2,3) 可变可视密码图像形变和图像恢复情况Table 1 Image deformation and image restoration for (2,3) variable visual cryptography 如果对一个N ×N 大小的秘密图像进行加密, 本方案的分存图的个数为 n, 分存图大小为 N ×N ×m/r, 当r = m 时, 该加密就是像素不扩展可视密码; 当r > m 时, 该加密得到的就是分存图像缩小的可视密码 (r 的增大会降低解密图像的对比度); 当 r < m 时, 该加密得到的就是分存图像扩大的可视密码.本方案与其他方案的对比如表2 所示. 表2 本方案与其他方案比较Table 2 Comparisons of this scheme with other schemes 本文提出任意点加密的可视密码, 即可变可视密码(VVC), 一方面它解决了传统可视密码像素扩张的问题; 一方面它非常灵活, 能使分存图像小于加密图像、等于加密图像或大于加密图像, 从而能有效减少存储空间, 或在存储空间和图像质量之间找到一个平衡点. 当r 较小时, 本文提出的可变可视密码加密的效果都非常好.当 r 较大时, 会出现图像边界模糊的现象, 如何避免边界模糊是我们今后的工作, 如何设计出能够较好的应用于灰度和彩色图像的可变可视密码,也是我们今后的工作.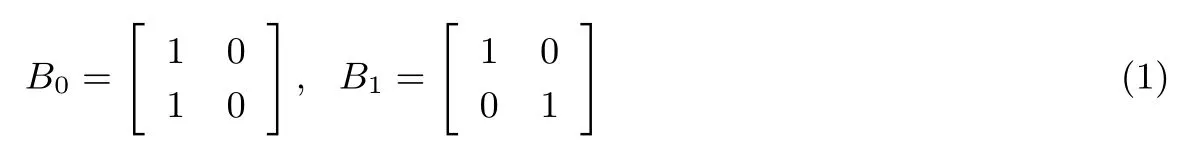
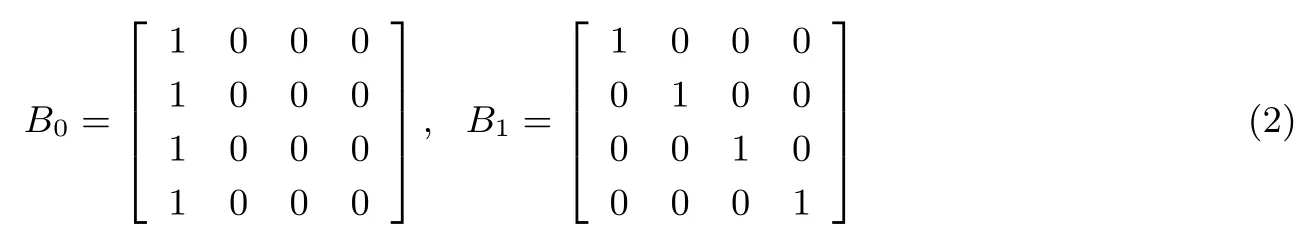
3 可变可视密码实现算法
4 可变可视密码证明
5 可变可视密码实例







6 总结与展望
