系杆钢拱桥安装及索力调节控制关键技术

李吉勇

上海市基础工程集团有限公司 上海 200433

系杆拱桥是由拱肋、系梁、吊杆等组合而成的结构体系。其力学体系是外部静定，内部为3+n（n为吊杆数）超静定结构。系杆拱桥的施工，除确保桥梁施工阶段的安全外，成桥的线形、最终的吊杆索力也是控制的关键。

目前，在实际应用中，吊杆张拉力的调整方法主要参照斜拉桥调索方法，分为正装法、倒装法、影响矩阵法、无应力状态控制法[1]。也有许多系杆拱桥施工控制和调索的案例，且取得了一定成果。然而在具体运用中，针对倒装法、影响矩阵法的吊杆索力控制，施工过程中还有许多细节和状态需要调整，才能最终达到比较合理的状态。

为此，本文结合具体工程实际，对系杆钢拱桥的施工和索力控制的调索方法进行进一步研究。

1 工程概况

上海北环路平申线系杆拱桥为跨度188 m的下承式钢结构系杆拱桥，全桥宽40 m。主桥桥面纵坡为2.49%，跨中竖曲线半径R＝4 000 m，切线长T＝99.6 m，外矢距E＝1.24 m。钢主梁中心间距28.671 m，高3.22 m，由钢主梁、中横梁、端横梁、小纵梁组成双主梁梁格体系。

主拱为提篮式钢拱箱，内倾12°，矢跨比为1/5，立面矢高为37.6 m，拱肋轴线采用二次抛物线，拱肋截面采用矩形截面，宽2.2 m，高2.8 m；梁与拱通过吊杆连接形成系杆拱桥结构。吊杆索体采用PES（C）7-109锌铝合金镀层平行钢丝拉索，吊杆在顺桥向间距 9 m，全桥共设36根（图1、图2）。

图1 系杆拱桥立面布置

图2 系杆拱桥平面布置

2 主桥安装施工关键技术

2.1 节段分段划分及临时支架设置

本桥跨度较大，钢拱桥安装采用先梁后拱的原位拼装法施工。由于跨度较大，主梁和拱肋采用分段吊装施工，各节段分段长度及质量统计如表1所示。同时考虑大治河通航需求，在跨河位置合理设置临时支架支撑（图3）。

表1 主梁及拱肋节段划分统计

图3 拱桥分段及临时支架布置示意

水中支架下部采用φ 820 mm×12 mm钢管作桩基础，每组4根，2×2布置，纵横向间距均为3.5 m，其上设双层双拼HN700 mm×300 mm型钢平台，平台上方搭设拼装支架，拼装支架采用φ478 mm×8 mm的钢管作为立柱，每组4根，2×2布置，标准长度为12 m，采用∠100 mm×10 mm角钢连接成格构体系。拼装支架顶部为双层HN700 mm×300 mm型钢横梁，下层为双拼结构，上层为单根结构，横梁顶部设置φ273 mm×6 mm钢管小立柱支撑，用于调节标高。拱顶位置横梁上设置HN700 mm×300 mm斜撑，用于支撑拱肋内倾。

中跨合龙段拱肋长度达78.4 m，单片拱肋重达220 t，为确保合龙段拱肋安装的稳定，在跨中已安装主梁上设置临时支架。

同时，为确保支架的稳定，通过斜向钢绞线缆风绳将跨中支架和两侧设有桩基支架及桥面系连接，如图4所示。

图4 合龙段拱肋跨中临时支架及斜向缆风绳示意

2.2 主桥吊装施工步骤

根据本桥梁工程结构特点和现场航道通航要求，在航道中间位置预留宽67 m的通航孔，两侧打钢管桩，采用水中浮吊全支架原位拼装的施工工艺。

根据现场施工条件，采用先梁后拱的安装顺序，具体如下：

1）采用150 t浮吊吊装定位4个拱脚节段，再吊装定位端横梁节段。

2）采用150 t浮吊吊装定位两侧的ZL1和ZL3主梁节段，主梁节段吊装定位后，进行相应小纵梁、横梁和挑臂的定位及安装。

3）300 t浮吊进场，采用2台浮吊抬吊定位主梁合龙段ZL2，主梁合龙后完成剩余小纵梁、横梁和挑臂的定位及安装。

4）用钢丝绳将拱肋支架与桥面系横梁相连，确保拱肋支架稳定。

5）采用浮吊吊装两侧拱肋节段GL1和GL3；节段拱肋吊装定位后，进行相应拱肋横撑定位及安装。

6）采用600 t浮吊抬吊定位拱肋合龙段，即GL2节段。7）采用浮吊安装剩余风撑和装饰板。

2.3 结合安装施工的系杆拱桥索力控制难点分析

在梁、拱安装好后进行吊杆索力张拉。由于梁、拱中跨跨度较大，且主梁跨中存在临时支架，导致主梁跨中挠度较大（图5），后续吊杆索力张拉时需考虑主梁挠度及主梁线形平顺的影响。

图5 主梁和中横梁变形示意

另外，节段跨度大、质量较重，临时支架施工阶段反力较大，后续临时支架落架体系转换时，会导致主梁及拱肋吊杆的应力重分布，给吊杆索力的控制带来不利影响。因此，如何在规避支架落架对吊杆内力影响的同时控制好全桥线形，是本桥施工控制的难点。

3 系杆钢结构拱桥初张拉索力控制关键技术

3.1 索力调节主要方法及误差分析

对于系杆拱桥吊杆成桥索力确定，常用的方法有刚性支撑连续梁法、力平衡法、刚性吊杆法、最小弯曲能法、影响矩阵法[2-3]。本工程设计时已明确了成桥索力，为此，索力的张拉调节以设计给定的成桥目标索力控制。

在吊杆张拉索力控制中，常用的吊杆索力控制方法有倒拆法、正装迭代法、影响矩阵法（通常在二次调索中应用）等。在真正实施过程中，理论计算和现场实际张拉测量结果往往有稍许误差。

结合相关吊杆张拉调索控制案例经验，分析总结其误差产生原因主要有：自重误差，结构刚度误差，边界约束误差，体系转换、应力重分布误差，工况、时间误差。

为了减少误差，现场施工控制时需采取相应措施，如表2所示。

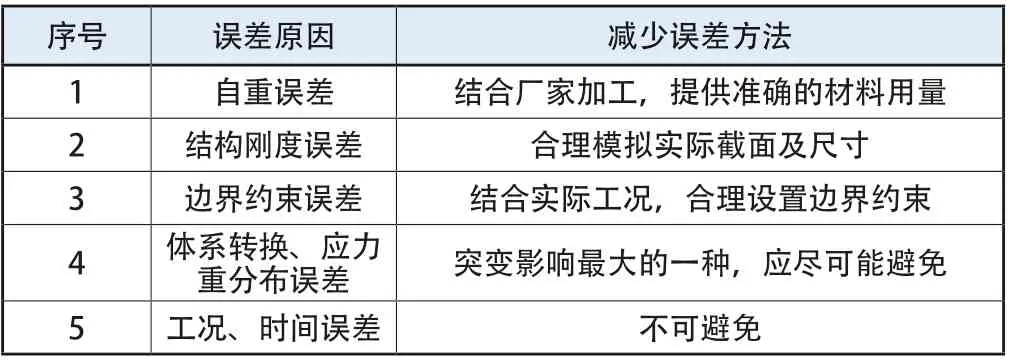
表2 误差原因及分析方法

综合分析，在以上几种误差类型中，体系转换、应力重分布引起的误差对吊杆内力影响最大。因体系转换，吊杆内力变化具有不确定性，为了减少吊杆索力调节的难度，应尽量控制吊杆索力张拉与调节在恒定的约束条件与体系内。

3.2 结合倒拆法的吊杆初张拉索力控制

为了尽量减少调整甚至不需要调整，一般先规定吊杆施工阶段信息，利用倒拆方法得到每根吊杆的初始张拉力。然后依照既定的顺序，按照上述初始吊杆张拉力张拉吊杆，如此张拉得到的最终状态，理论上就是设计时想得到的状态。

3.2.1 模型建立

运用有限元软件Midas civil对全桥整体结构建立包含施工阶段分析的三维有限元模型。有限元模型中系梁、拱采用梁单元模拟，吊杆采用桁架单元模拟，桥面板采用板单元模拟（图6）。

图6 桥梁三维模型

边界条件为4个永久支座：固定支座、横桥向活动支座、纵桥向活动支座、双向活动支座。所有系梁的拼装支架采用只受压弹簧模拟。

3.2.2 吊杆张拉工况确定及倒拆

主梁、主拱合龙好后，根据结构及临时支座约束特性，本桥结构成对角对称形式。同时，结合现场实际施工条件，吊杆张拉采用共轭对角张拉形式。

实际施工工况为：1#、18#张拉→北2#、南17#→南2#、北17#→北3#、南16#→南3#、北16#→北4#、南15#→南4#、北15#→北5#、南14#→南5#、北14#→北6#、南13#→南6#、北13#→北7#、南12#→南7#、北12#→北8#、南11#→南8#、北11#→北9#、南10#→南9#、北10#。结合实际施工工况进行吊杆倒拆（部分模型如图7、图8所示），即可得到吊杆初张拉索力。

图7 拆南9#、北10#吊杆后剩余吊杆索力

图8 拆北2#、南17#吊杆后剩余吊杆索力

3.3 考虑主梁线形及临时约束的初张拉索力控制

理想的倒拆，在吊杆初张拉完成后，将吊杆内力再增加后期二期荷载的影响，便能较好地达到吊杆的成桥索力状态。

为方便后续吊杆内力调整，结合倒拆法，在吊杆全部初张拉完成后，要求主梁和拼装临时支架解除约束，在三维计算模型中控制主梁和临时支座腾空位移0～15 mm（图9、图10）。

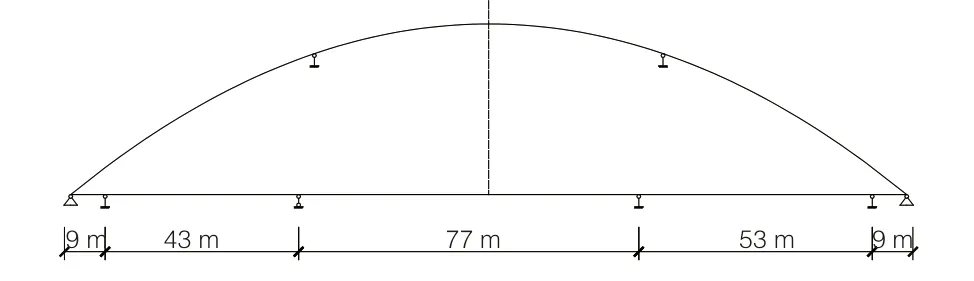
图9 吊杆张拉前桥梁结构约束状况

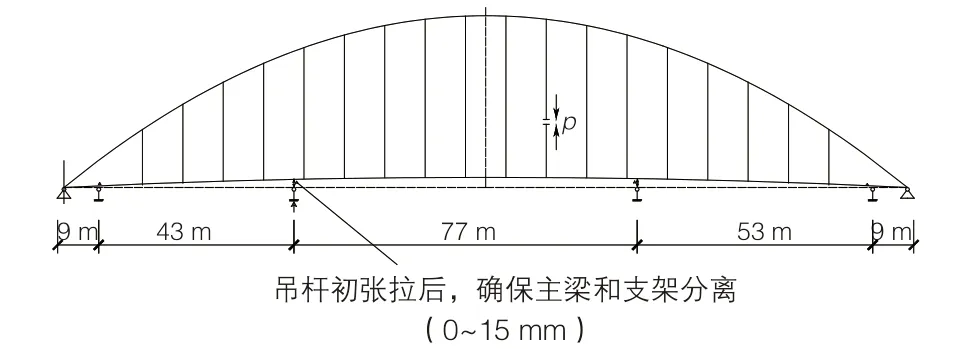
图10 吊杆初张拉后主梁变形及体系转换情况示意

3.4 吊杆张拉工况及张拉索力确定

结合初张拉索力及附加体系状况，将倒拆吊杆张拉力通过重复迭代法进行分析计算，并采用正装验算方法确定各施工状态下的吊杆受力和变形等控制数据，将误差控制在允许范围内，得到合适的初张拉力值。

4 基于影响矩阵的二次调索优化控制

4.1 需二次调索的误差分析

初张拉完成后，在实际施工过程中还需进行桥面板施工、水平索张拉、挑臂安装等。由于桥面板混凝土自重误差、温度变化、水平张拉、收缩徐变等影响，实际成桥索力和目标索力局部还是有些许差距。

为此，对其中局部成桥索力和目标设计索力差别较大的吊杆还需要进行二次调索。

4.2 影响矩阵施调向量计算

二次张拉调索不同于初张拉，由于二次调索时桥梁所有吊杆都已安装好，当单独调整某一吊杆索力时，该吊杆张拉会对已安装索力产生影响，而且每次索力调整都会对既有吊杆索力产生影响。这是二次调索最为烦琐的地方。目前，二次索力张拉常采用影响矩阵法进行调索。

影响矩阵法的基本思路是：根据具体结构选择关心的目标向量，利用有限元模型求出单位施调向量作用下目标向量的影响矩阵，从而建立典型方程：

式中：{P0}、{P}——受调向量，即结构调整时的目标向 量，{P0}为调整前的初始值，{P}为 期望达到的期望值；

{∆T}——施调向量；

[A]——结构对受调向量的影响矩阵。

本工程中受调向量和施调向量均取吊杆力向量，在确定吊杆张拉力初始值、目标值和影响矩阵后，通过求解方程（1）得到施调向量，以期达到结构的期望值。

计算吊杆张拉力影响单位矩阵[A]。单位矩阵和吊杆二次张拉顺序有关，针对二次张拉，拟考虑从跨中到两端拱脚的张拉顺序，每次同时对角张拉2根，顺序为9#、10#；8#、11#；7#、12#；6#、13#；5#、14#；4#、15#；3#、16#；2#、17#；1#、18#，对每根吊杆施加单位力1 kN，得到吊杆张拉力影响矩阵。

由于现场两端对称张拉，为了简化计算值，计算半跨1～9根吊杆的影响矩阵，同时由于拱脚刚度较大，吊杆力的改变量跟其长度应变量关系很大，靠近拱脚的吊杆上抬量很小，所以对其他吊杆的影响很小，几乎可以忽略。为此，简化其余吊杆力变化产生的影响范围为2～3根吊杆，得到简化单位影响矩阵。

4.3 二张索力调整控制

计算初始吊杆力列向量{P0}和目标吊杆力列向量{P}。通过正装法得到初始吊杆力列向量{P0}，即吊杆力调整阶段之前各吊杆的已存吊杆力；在设计吊杆力已知的情况下，通过倒推法得到目标吊杆力列向量{P}，即吊杆力调整阶段之后各吊杆的吊杆力。

求解式（1）得到施调吊杆力列向量{∆T}＝[A]-1{∆P}，需要特别注意的是，求得的{∆T}仅为吊杆力调整的增加值，实际施工时，需要在此基础上得到吊杆的千斤顶张拉力，用{N}表示，考虑到单侧2根同时张拉，则同时张拉第i-1号、第i号吊杆时，吊杆千斤顶张拉力{N}＝{P0i-1}+{∆T}，由于二次张拉也是分批张拉的，不能将18对吊杆一次同时张拉，因此，{P0}初始值也是根据二次调索工况顺序进行叠加。

5 成桥索力实测及目标索力情况

本桥通过倒拆法、正装重复迭代法分析等，最后结合影响矩阵进行二次调索优化控制，在二期恒载作用的结构施工完成后，测量得到吊杆索力的最终实际值。

通过对合理初张拉力值控制和二次调整，最终控制的成桥吊杆实测索力与目标索力误差在5%之内，最大偏差为4.95%，达到了系杆拱桥索力控制要求（图11）。

图11 全桥吊杆张拉完全

6 结语

本文以上海北环路平申线188 m系杆拱桥为背景工程，介绍了大跨度系杆拱桥安装及吊杆索力控制的关键方法，主要成果如下：

1）总结大跨度系杆钢拱桥合理的节段划分、原位拼装施工关键技术。

2）运用倒拆法合理确定了吊杆索力初张拉控制值，并明确了吊杆初张拉主梁线形及临时约束状态下的初张拉控制值，大大减小了后续工况体系转换的误差。

3）采用影响矩阵法，结合二次吊杆调索张拉顺序及对称张拉特点，简化和优化单位矩阵向量，精准快速地实现了吊杆二次索力调整，实现了索力的目标状态。

[1] 胡成,周力,李霞.基于无应力状态法的下承式拱桥吊杆张拉次序优 化[J].安徽建筑大学学报,2019(1):6-10.

[2] 张传龙,虞建成.系杆拱桥吊杆索力及施工张拉力确定方法[J].山东 交通科技,2011(6):51-53.

[3] 王战国,俞亚南,王伟,等.自锚式悬索桥吊杆索力优化的影响矩阵法 [J].中国市政工程,2005(3):68-69.