前房深度对正常眼轴白内障患者屈光度计算准确性的影响

李娟，朱珂珂

开封市中心医院眼科(河南开封 475000)

白内障手术已经进入到屈光手术时代，多焦点以及散光晶体的应用逐渐普及，这些高端人工晶状体对屈光度精准计算的要求越来越高。既往研究资料表明，在屈光误差可能因素中，眼轴长度测量的误差占54%，角膜曲率测量的误差占8%，而预测术后前房深度占20%～40%[1-4]，目前发现人工晶状体有效位置的预测(effective lens position, ELP)是影响术后结果的最主要因素。因此4代、5代公式都增加了前房深度(anterior chamber depth，ACD) 和其他参数来提高计算的准确性。关于ACD的相关研究国内较少报道，我们对此做了相关研究，现将结果汇报如下。

1 资料与方法

1.1 一般资料 选取2018年4月至2019年2月在我院行白内障手术的患者152例(164眼),其中男69例，女83例，年龄(64.15±7.42)岁，按ACD大小分为3组：A组ACD<3.0 mm(57眼)，B组3.5 mm≥ACD≥3.0 mm(55眼)，C组ACD>3.5 mm (52眼)。3组患者性别、眼别、年龄差异无统计学意义(P>0.05)，见表1。纳入标准：患者眼轴范围：22～26 mm，角膜曲率值范围：42.0～46.0 D，所有患者均植入Rayner 920H或970C非球面人工晶状体，术后最佳矫正视力(best corrected visual acuity，BCVA)≥0.8 。排除标准：眼部其他疾病，有屈光手术史的患者。

组别性别(例)眼别(例)男女左右年龄(岁)A组2724252265.62±7.76B组2524212463.04±6.97C组2626262666.53±9.85

1.2 方法 术前行IOLMaster700(ZEISS)检查，分别应用SRK/T、Holladay 2，Haigis、Hoffer Q、Barrett Universal Ⅱ公式计算IOL屈光度，人工晶状体常数采用ULIB网站优化常数。其中Barrett Universal Ⅱ公式采用在线计算(www.apacrs.org)，目标屈光度均设为0 D。所有患者均由同一医师手术，采用透明角膜缘切口行白内障超声乳化联合人工晶状体植入术，均植入Rayner 970C或920H非球面人工晶状体。术后至少1个月行主觉验光检查，并以等效球镜表示,计算平均预测误差(refractive prediction errors, RPE)、平均绝对值误差(mean absolute error，MAE)、绝对值误差中位数(median absolute error,MedAE)，所有验光均由同一医师完成。以人工晶状体1.0 D折合于框架眼镜0.7 D为原则计算屈光误差[5]，RPE=植入的IOL度数+验光等效球镜/0.7-术前计算的IOL度数。

1.3 统计学方法 采用SPSS 22.0统计软件，组间比较采用Friedman检验，组内比较采用Bonferroni校正，误差范围百分比差异比较采用Mann-WhitneyU检验，以P<0.05为差异有统计学意义。

2 结果

2.1 SRK/T和Hoffer Q公式的RPE组间比较 SRK/T和Hoffer Q公式的RPE组间比较差异有统计学意义(P<0.05)，而Holladay 2、Haigis和Barrett Ⅱ公式的RPE组间比较差异无统计学意义(P>0.05)。其中A组患者Barrett Ⅱ公式 的MAE和MedAE明显低于其他公式，与其他公式比较差异有统计学意义(P<0.05)，见表2，在RPE±0.25D、±0.5D内的比率也显著高于其他公式(P<0.05)，见表3。

项目SRK/THolladay2HofevQHaigisBarrettⅡRPE-0.21±0.62-0.11±0.43-0.19±0.650.08±0.46-0.13±0.48MAE0.48±0.420.47±0.420.48±0.430.50±0.420.37±0.37MedAE0.40.30.320.250.21

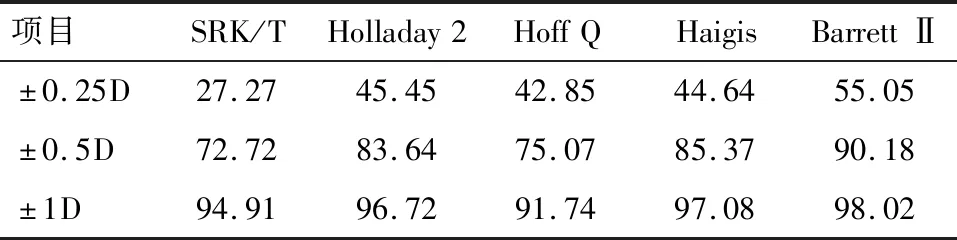
表3 A组患者术后不同公式的屈光误差范围 %

2.2 B组患者术后不同公式的屈光误差 B组患者各个公式间的RPE、MAE及MedAE比较均差异无统计学意义(P>0.05),见表4、5。

2.3 C组患者术后不同公式的屈光误差 C组，Barrett Ⅱ公式的MAE较低为0.35±0.43，而Hoffer Q公式的MedAE较高为0.78，与其他公式的比较差异有统计学意义(P<0.05)，见表6。Hoffer Q公式在RPE±0.25D、±0.5D内的比率显著低于其他公式，与其他公式的比较差异有统计学意义(P<0.05)，见表7。

项目SRK/THolladay2HofferQHaigisBarrettⅡRPE0.07±0.300.11±0.390.16±0.540.07±0.51-0.10±0.37MAE0.28±0.120.27±0.290.38±0.400.37±0.340.25±0.28MedAE0.280.240.210.210.16

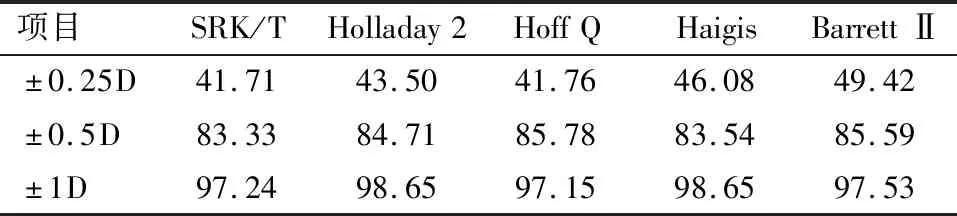
表5 B患者术后不同公式的屈光误差范围 %

项目SRK/THolladay2HofferQHaigisBarrettⅡRPE0.31±0.670.18±0.640.38±0.850.07±0.84-0.12±0.53MAE0.64±0.480.57±0.550.71±0.600.56±0.700.35±0.43MedAE0.480.340.780.410.32

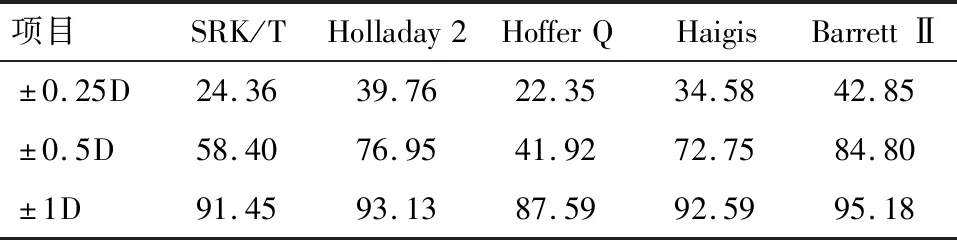
表7 C组患者术后不同公式的屈光误差范围 %

3 讨论

目前发现人工晶状体有效位置的预测是影响术后结果的最主要因素，而ACD是影响ELP的直接因素，之前的计算公式仅考虑眼轴和角膜曲率，以标准模型眼来计算其位置和屈光度。而人工晶状体虹膜隔的位置因人而异，不同种族差别较大，其在眼内轻微的变化就会引起患者巨大的屈光误差，尤其在高端人工晶状体上表现明显。本研究发现ACD在3.0～3.5 mm时，也就是正常前房深度时，所有公式均表现出了良好的计算准确性。3代公式(SRK/T、Hoffer Q)、4代公式(Holladay 2，Haigis)、5代公式(Barrett Ⅱ)之间无明显差别。而在浅前房和深前房组SRK/T、Hoffer Q公式的计算误差明显高于其他公式，可能与其公式的计算变量仅有AL和K值，而无ACD，其他公式均有ACD这个变量有关。而BarrettⅡ公式在浅前房组屈光误差范围±0.25D、±0.5D分别达到了55.05%、90.18%，不仅高于其他公式，甚至高于B组的的49.42%、85.59%，C组屈光误差范围±0.25D、±0.5D达到了42.85%、84.80%的，同样高于其他公式，与正常前房组的计算准确性比较接近，显示出前房深度变化对BarrettⅡ公式影响较小。

本研究为排除其他异常眼前节参数对IOL计算的影响，患者筛查上排除了异常AL和异常角膜K值的患者。已有很多文献报道过长和过短的AL会引起患者的屈光误差[6-8]，所以我们把眼轴范围设定在22～26 mm。Reitblat等[9]对79例角膜K值>46.0 D和92例角膜K值<42.0 D的患者分别应用本研究的5个公式以及Holladay 1、Hill-RBF、Olsen在内的8个公式进行了屈光误差分析，发现K值>46.0 D时的平均屈光误差为(-0.36±0.35)D，K值<42.0 D时的平均屈光误差为(0.10±0.37)D。因此本研究在选择患者时把K值范围设定在42.0～46.0 D。李朝辉等[10]认为超声乳化白内障摘出术后2周角膜散光稳定，术后2～4周屈光状态稳定，可进行最终验光配镜。因此我们设定的术后验光时间为至少1个月，本研究中最长有术后2年的患者，并没有统一固定时间，这样就大大减少了搜集样本的难度，提高了样本的可靠性。Melles等[11]对18 000余例白内障患者进行分析，发现当ACD<3.0 mm时，BarrettⅡ公式计算准确性最佳，当ACD在3.0～3.5 mm时，所有公式的准确性无明显差别，这与我们的研究结果基本一致；当ACD>3.5 mm时Haigis公式计算准确性最佳，BarrettⅡ公式次之，这与我们的研究结果略有不同，考虑可能为我们的样本量较小，与他的大样本研究对比统计误差所致。

本研究应用的BarrettⅡ公式为第5代人工晶状体计算公式，是基于近轴光线追踪技术，厚晶状体模型的理论公式[12]，在多变量公式中ACD的变化对其影响较小。Kane等[13]对3 421例患者的研究发现BarrettⅡ公式在长、中、短眼轴的绝对值误差比其他公式都要小，在所有患者中屈光误差范围±0.25D、±0.5D、±1D分别占43.5%、72.3%、94.5%，明显高于其他公式，由此认为在眼轴超过22 mm时，BarrettⅡ公式比其他公式具有更高的计算准确性。国内研究[14-15]也认为BarrettⅡ公式在高度及超高度近视患者的屈光度计算上相比其他公式具有更高的准确性。

本研究也有一些局限性，样本量相对较小，未能对浅前房患者的晶体厚度进行相关分析及术后前房的对比研究，计算公式不全面未对Hill-RBF、Olsen等其他公式进行对比分析。

总之，前房深度对Barrett Ⅱ公式计算准确性的影响较小，对于深前房和浅前房的患者可考虑术前应用Barrett Ⅱ公式计算减少屈光误差。