基于互相关差分的多普勒频率估计算法

王奉帅,王华青,董仁智，王 晔

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.中科恒运股份有限公司，河北 石家庄 050000；3.电子科技大学，四川 成都 611731；4.中国人民解放军95861部队，甘肃 酒泉 735018)

0 引言

在卫星导航接收机中，信号同步模块是一个非常重要的单元，它首先对接收到的卫星导航信号进行同步，然后解析导航信号中的导航电文，最后根据导航电文进行定位[1]、测速以及授时解算。信号同步模块通常分为捕获和跟踪2个部分[2-5]，捕获的目的是确定当前可见卫星，并估算出接收到导航信号的码片时延以及多普勒频率，接收机再将这些参数作为跟踪模块的初始值进行跟踪处理。

信号捕获是通过对接收到的卫星信号和接收机产生的多个本地信号进行互相关运算来完成的，当互相关运算得到的计算值大于设置的门限值时，就认为该值对应的本地信号与接收信号一致。在捕获阶段接收机估计出来的频率误差在几百Hz左右，对跟踪模块来说，输入的初始化值精度太差，容易造成跟踪失败。因此，需要在捕获阶段进行优化运算来提高频率估计的精度，其中文献[6-7]中都介绍了频率估计方法。目前频率估计主要分为基于相关运算的算法和基于快速傅里叶变换的算法2类[8-11]。本文提出了一种新的多普勒频率估计算法[6]，该算法属于第1类频率估计算法，它对2个连续差分组合的相位再次进行差分运算，克服了传统相位卷绕带来的频率估计模糊度问题，对2次差分后得到的结果进行求角运算可以提高多普勒频率的估计精度。

1 多普勒频率估计原理

卫星导航接收机接收到卫星导航信号并经过AD转换后，信号的具体形式可以表示为：

cos[2π(fIF+fd)nTs+φ]+nw(n)，

(1)

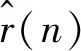
sm+ωm，

(2)

式中，序号m为第m个相干积分区间[(m-1)N,mN]；N=⎣TcohFs」为相干积分时间Tcoh内的采样总数；sm，ωm分别为信号和噪声部分，假设在很小的时间间隔内，频率是固定的，式(2)可以写为[12]：

(3)

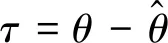
2 多普勒频率估计原理

在没有噪声的情况下，根据式(2)和式(3)，2个连续相关区间的相位差为：

(4)

基于式(4)，许多文献介绍了估计多普勒频率的方法。

2.1 经典Kay算法

文献[16]中介绍的多普勒频率算法是根据2个连续相干积分区间的相位差估计出来：

(5)

式中，总观测时间T0=M·Tcohs；M为观测区间的个数。该方法基于相位解卷绕算法，具有计算复杂度低的优点，但是该算法需要在高载噪比的场景下才能估算出精确的多普勒频率。

2.2 常规差分结合算法

文献[17]介绍了常规差分组合算法(Conventional Differential Combination，CDC)，仿真证实该算法在低载噪比的场景下也能正常估算出多普勒频率：

(6)

CDC与Kay算法的主要区别在于求角运算和积分运算的计算顺序，求角函数是非线性函数，但是积分运算是线性噪声滤波器，如果积分运算在求角运算之前，会提高积分运算对噪声的滤波性能，因此CDC算法性能优于Kay算法。

2.3 常规差分组合修正算法

文献[13]给出了对不同相干积分区间进行组合运算的常规差分组合修正(Modified Generalized Differential Combination，MGDC)算法。该算法的输出是将不同跨度的区间进行组合，能够提高捕获灵敏度，Ai定义为2个跨度相差为i的相干积分区间的差分组合：

(7)

不考虑噪声的情况下，将式(3)带入式(7)，可以写为：

(8)

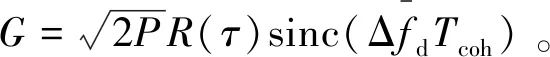
因此，多普勒频率可以写为：

(9)

式中，ωi由各跨度组合个数确定。文献[6]的结果说明，可以利用的跨度组合个数不止一个，用到的组合数越多，频率估计结果越好。

上述所有方法都利用了求角运算来估计多普勒频率，但是求角运算解算出来的相位是卷绕的。求角运算式为：

arg(Ce2kπ+φ)=φ;∀φ∈[-π,π],∀k∈Z。

(10)

因此，如果实际的相位是非卷绕的(k≠0)，估算出来的相位误差是2π的倍数，为了避免该问题，输入的相位必须在区间[-π,π]内。

如果搜索空间为并行码相位搜索捕获[18]，可以得到：

(11)

式中，ΔfStep为多普勒频率搜索空间的步进大小。式(11)表达了估计多普勒频率前的变化区间。根据式(4)～式(6)，Kay和CDC算法的卷绕相位约束范围为：

(12)

同样对于MGDC算法，相位约束表示为：

(13)

MGDC算法跨度限制示意如图1所示。

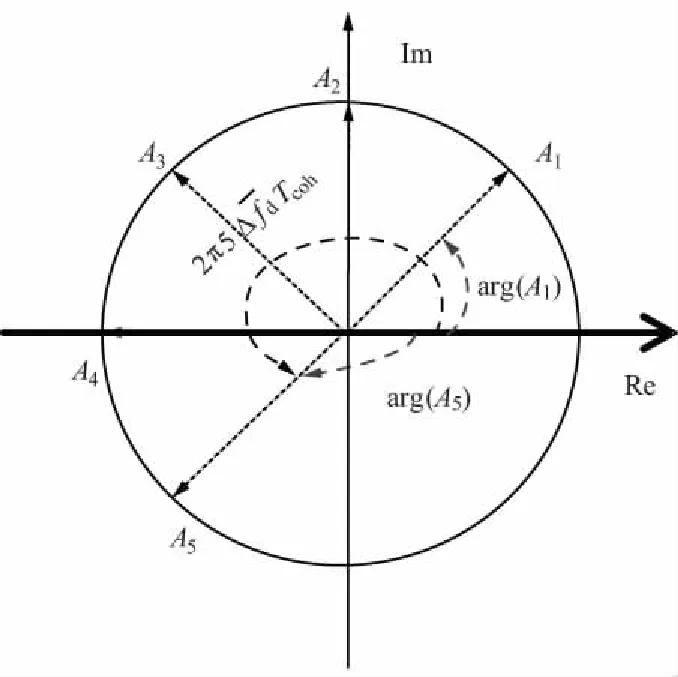
图1 MGDC算法跨度限制示意Fig.1 Limit of modified generalized differential combination methods

2.4 相干积分组合差分算法

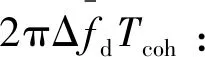
(2≤i≤M-1)。

(14)

由式(14)可以看出，相位表达式里的区间号被消除了，因此利用A1,i来估计多普勒频率不会存在相位卷绕问题[6]。

Ai可以认为是相关值的一阶差分，A1,i可以认为是二阶差分，通过式(14)，对于固定的相关值，跨度区间越大，用到的相关值个数越少，幅度Gi包含了每个组合的信息量，因此可以用来作为频率估计新算法的加权值：

(15)

相干积分组合差分算法中，M值越大，计算量越大，在跟踪过程中会产生很大的时延，导致降低高动态下频率估计的准确度。该算法既避免了相位解卷绕问题，组合个数也没有受到限制，因此在多普勒相位较大的情况下更有效，而且不需要增加频率搜索范围，特别是载噪比小的情况下，增加相干积分时间Tcoh可以提高同步模块的灵敏度。

3 性能分析

仿真条件：导航信号经混频后，正弦载波信号中频fIF为46.42 MHz，多普勒频率fd为125 Hz，采样频率fs为62 MHz，对相同信号分别用上述算法进行100次多普勒频率估计，具体的估计精度如图2所示。

图2 多普勒频率估计算法性能比较Fig.2 Performance of Doppler frequency estimation methods

由图2可以看出，在低载噪比场景下Kay算法和CDC算法估计的多普勒频率较差，虽然New MGDC算法比MGDC算法稍好，但是MGDC算法的差分组合跨度过大，会引入一个固定误差，在跨度为5的情况下，解算出来的多普勒频率是错误的，而New MGDC不存在这个问题。

由式(5)和式(6)很容易计算出Kay算法以及CDC算法的运算复杂度。假设有M个互相关运算，用α表示乘法运算，β表示求和运算，对于本文给出算法的运算复杂度为：

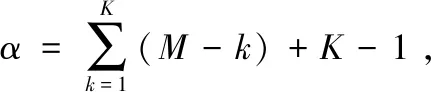
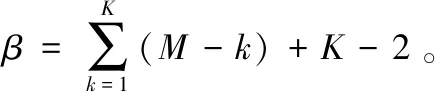
上述算法的计算复杂度如表1所示。

表1 各算法计算量对比

4 结束语

本文给出了一种新的多普勒频率估计算法，虽然是基于MGDC改进的算法，但是并不受相干积分区间跨度的约束，与传统算法相比，该算法可以获得精度更高的信号多普勒频率，而且不需要计算出载波频率。虽然该算法的运算复杂度比其他算法要高，但是为信号捕获阶段提供了高精度的频率估计初始值，减小了捕获阶段的搜索范围，降低了捕获阶段的复杂度。