三相不平衡配电网中电动汽车充电问题的混合整数非线性规划模型

文/汤 赟（上海理工大学）

一、背景介绍

近年来，在国家政策大力支持下，电动汽车在日常生活中的使用逐年增加。为了提升电动汽车充电桩覆盖率，加密汽车充电网点，需在已有的三相不平衡配电系统的节点上，添加充电站为电动汽车供应能源。考虑到电动汽车充电的本质是对汽车内置的可充电电池组充电，因此，在充分考虑电能传输的安全性和可靠性的基础上，可以将该电动汽车视作负载接入三相不平衡的配电系统中进行运行方式优化。

在系统实际运行中，电网运行方式如果没有充分考虑安全性和可靠性，可能会导致线路过载、电压超限、功耗增加等一系列问题，因此我们所建立的三相不平衡系统必须充分考虑安全运行方面的要求。过去，常见的模型建立方式是将可充电能最大化及功率损耗最小化作为模型优化目标，在不考虑电动汽车对配电网影响的前提下，以充电成本最优作为目标函数，建立一个应用混合整数线性模型优化的实时负载管理运行模式来实现电动汽车充电优化。

为了进一步提升算法精度，使之更符合配电系统运行的实际情况，本文建立了一个混合整数非线性（MINLP）模型，来代替过去常用的混合整数线性（MILP）模型[1]，并以最小化功耗作为优化目标建立三相不平衡配电系统的目标函数。在三相不平衡配电系统运行中，实时电流的实部和虚部必须始终满足平衡条件，用电路中的电压与电流的实部与虚部的乘积之和分别列出电路中的有功功率与无功功率的表达式；配电系统中的每一条独立的回路必须满足基尔霍夫电压定律；线路上的电压和电流必须符合安全性要求，即不能超过电压限值和电流容量。据此，本文建立了三相不平衡配电系统MINLP 模型。本模型中，将线路电流分别表征为与线路有功功率、线路无功功率、电压实部及电压虚部四个参量相关的函数，用牛顿—拉弗逊方法将其电流的非线性表达式近似线性化，并最小化实际值和估算值之间的误差，在利用线性分割法分别线性化电路的电流和电压限值后，再将电动汽车作为负载代入优化算法模型进行规划。

二、假设条件与参数设置

本文致力于为配电系统解决电动汽车充电问题，使其在最优的成本下，满足实际可操作的安全约束条件。为此作以下假设：（1）在参考节点上有一个发电机可以提供足够的有功和无功功率；（2）只有PQ 节点有负载，并且每个PQ 节点都有三相负载；（3）独立负荷与一个相位相关，同一相位关联的负荷可以线性叠加；（4）电动汽车应当由确定节点的确定相位充电；（5）充电开始前，电动汽车的初始状态已知。

在模型运行过程中，必须满足电压幅值限制、发电机限制和最大电路电流等限制条件。为建立模型，定义以下参数：F表示三相集合 {A,B,C}，N表示节点的集合，T为时间间隔的集合。定义模型中的常数项：表示节点n在t时刻的供能成本，β表示电动汽车供能削减成本，△t表示时间间隔t的持续时间，分别表示节点n处的电动汽车能量容量和初始充电状态，表示节点n处电动汽车的最大功耗，分别代表时间间隔t中节点n处的相位f的估算电压的实部与虚部。另外，对需要进行优化的变量进行定义：分别表示时段结束时节点n处电动汽车的能量和能量削减，分别表示时间间隔t中节点n处相位f上电动汽车供应的电流的实部与虚部，表示时间间隔t中节点n处电动汽车的有功功耗，分别表示时间间隔t中节点n处相位f上电压的实部与虚部。

三、三相不平衡配电网的电动汽车充电问题

基于稳定状态下的配电系统，电动汽车作为一个复杂的负载，可以被加入到确定节点的每一相中。三相不平衡配电网的电动汽车充电问题本质上可以理解为一个混合整数非线性规划（MINLP）问题。该问题以最小化充电成本为目标，同时满足电动汽车本身以及配电网的各种约束条件，最终确定电动汽车的最优充电计划。为便于求解，本文将此问题线性化，最终形成一个混合整数线性规划（MILP）问题。

1.目标函数

作为电动汽车充电配送端，降低充电成本是主要目的，其中包括注入电动汽车的功耗，以及由于未能有效规划充电时段和充电能量而导致的储能装置的能量削减，由此给出以下的目标函数公式：

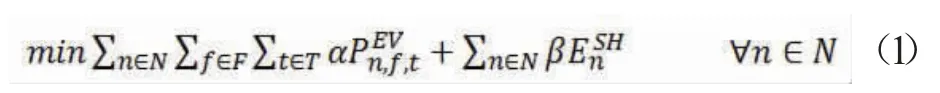
2.电动汽车的约束条件

公式（2）和（3）表示电动汽车充电的能量；公式（4）表示电动汽车的能量容量、充电量、初始能量状态及能量削减四者之间的能量守恒；公式（5）和（6）分别表示电动汽车需要的有功功率和无功功率。

电动汽车的有功功率和无功功率需要被线性化，近似地用一对运行点的估计值来建立公式（7）和（8）。

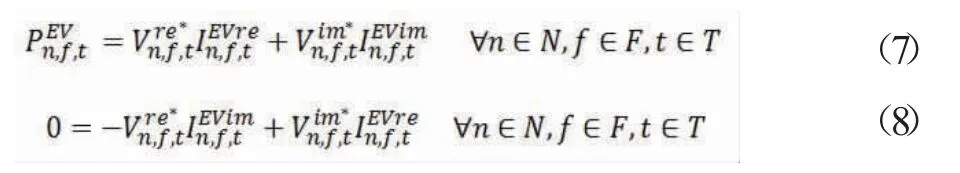
电动汽车的初始充电状态可以估算获得[2-4]。

四、包含电动汽车充电问题（EVC）的三相不平衡配电系统优化问题的实例

在5 节点中压等级（13.8kV,100kVA）的配电系统中建立前述的模型，如图1 所示。此中压等级的配电系统的数据建立在IEEE 34 节点模型[5]的基础上。它的最大和最小电压幅值的标幺值分别为1.00p.u.和0.90p.u.。这个模型可以用CPLEX[6]提供的编程语言表达出来[7]，并使用CPLEX 在带有Intel i7 3520 处理器的计算机上进行求解。

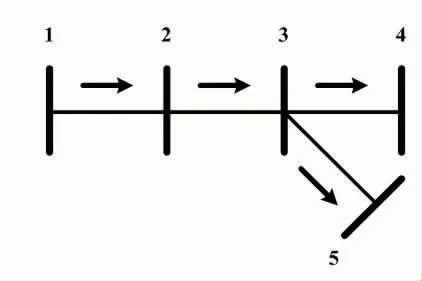
图1 5节点配电系统的拓扑结构

假设电动汽车电池容量为50kW·h，最大功率为10kW[8]；参数代表节点n处的电动汽车能量容量，它是被贮存电池中的能量，而不是额定容量；系数β取10元/kW·h。假设每个节点的每一相位（不包括参考节点和无负载的节点）在 17：00 到 01：00 的时间段内需要的能量容量为50kW·h，且每小时10kW·h。α 是供给电动汽车的能源价格，以上海电价为例，其中，假设17：00 到21：00时间段为 0.617 元 /kW·h，21：00 到 01：00 时间段为 0.317元/kW·h。

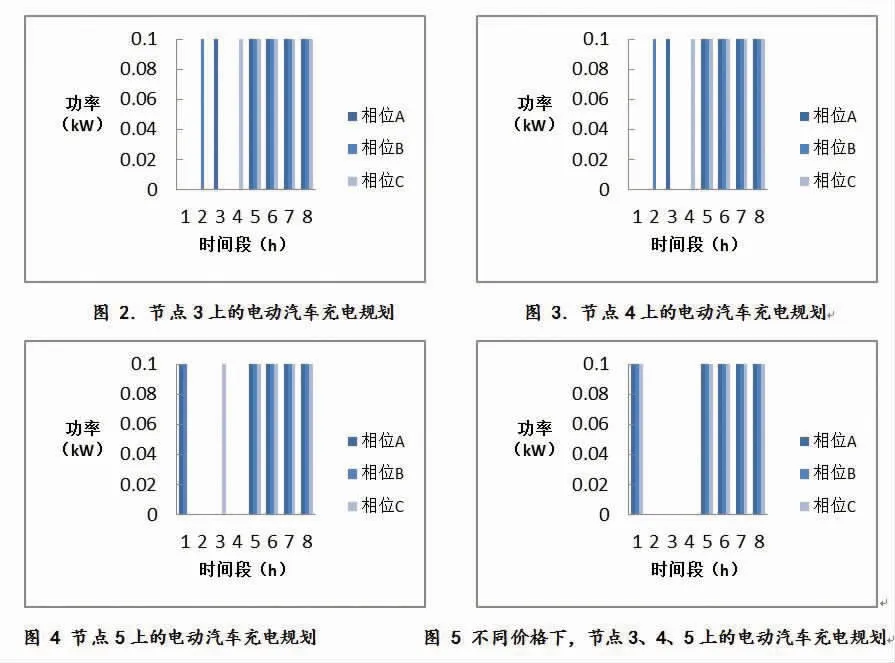
图2 节点3 上的电动汽车充电规划

图3 节点4 上的电动汽车充电规划

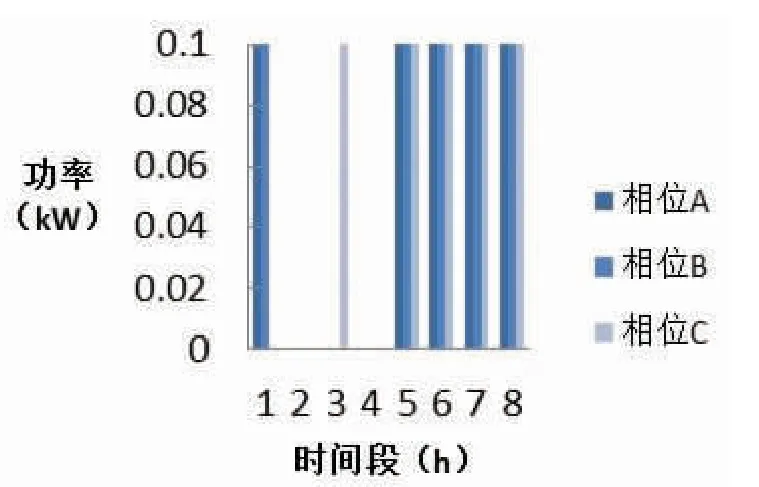
图4 节点5 上的电动汽车充电规划

图5 不同价格下，节点3、4、5 上的电动汽车充电规划

根据线性化的MINLP 模型优化电动汽车充电实例的模拟结果中所呈现出在时间段17：00 到01：00 内电压和电流标幺值，绘制出以下几个节点上的配电功率结果。图2、3、4 分别呈现了从 17：00 到 01：00 的 8 个时间段里节点3、4、5 每一相位上的功率，可以从中找到最低成本的充电模式。假定每小时价格不同，例如在给定的17：00到 21：00 的 4 个时间段内，价格分别为 0.70、0.90、1.00、0.80 元 /kW·h，21：00 到 01：00 的 4 个时间段内价格为0.30 元 /kW·h，可以发现前 10kW·h 在 17：00 到 18：00 之间完成充电，余下的 40kW·h 在 21：00 到 01：00 之间完成充电可以将成本降到最低，如图5 所示。因此，使用线性化的MINLP 模型拟合所得结果，符合最优规划结果。

更进一步，我们可以将此模型拓展应用到拥有更多节点、更长时间间隔、更大电动汽车充电容量的配电系统中，只需在算例中修改节点和节点数量即可，代入每一相位上不同用户在不同时间段的充电电量需求，即可通过线性化的MINLP 模型得到满足线路安全性和可靠性约束的最小成本的电动汽车充电优化结果。

我国城市用电有波谷和波峰两种不同电价，还要考虑工作时间内和工作时间外用户对电动汽车充电位置的不同需求，在实际操作中会存在时间段及地域上的差异。因此，在模拟过程中，会发现由于负载接入的节点变化较大而带来输配电量波动，比5 节点的配电系统更加复杂。

五、结语

综上，将MINLP 模型转换为MILP 模型是可行的，这样在三相不平衡配电系统拟合中可以减少运行时间，提高运算精确度。根据电动汽车充电实例，可以在今后的工作中对以下几个方面加以进一步研究：在满足馈电线路安全性前提下，可以选择最优的电动汽车充电容量；依托电动汽车充电的优先级，用户可以主动选择充电的时间段；可以在用电高峰期改变电动汽车电池的充电速率，从而提升配电系统对输配电的调控能力。