基于I/F+A/D的高分辨率模数转换电路

黄武扬，吴 一，黎 坤

(中国航天第九研究院十六研究所，陕西西安 710100)

0 引言

在惯性导航系统中，加速度计用来测量运载体的加速度。近年来，随着加速度计精度的提高，系统对于加速度计模数转换(I/F)电路也提出了更高的要求。传统的I/F电路由分立器件搭建，要想得到更高的分辨率，必然要提高电路的工作频率，然而这样又会导致器件的开关特性变差，进而导致线性度变差[2]。另外，对现有I/F电路来说，量程与分辨率互相矛盾，不能同时满足大量程和高分辨率的需求[4]。A/D芯片具有较高的采集速度，能够直接将模拟量转换成数字量，但它的非线性度较低[2]。因此，本文将I/F电路与A/D芯片相结合，设计了一种既不损失其他性能指标，又具有高分辨率的模数转换电路。采用FPGA实现逻辑控制，提高电路的可靠性；采用DSP进行数据处理，提高电路的运算速度；采用FIR滤波对输出数据进行平滑，提高电路的稳定性。

1 电路设计

1.1 工作原理

高分辨率模数转换电路是基于电荷平衡原理建立的。加速度计的输出电流对积分器充电，基准反馈电流对积分器放电，使积分器上的电荷保持平衡。通过对放电电流的量化和对积分器残余电荷的测量，就能得到输入电流的大小。图1为电路的原理框图。

电路由积分器、比较器、电子开关、2路反馈恒流源、A/D采样电路、FPGA、DSP组成。输入电流Iin和反馈电流±Iref同时流入电路，使积分器输出电压Uout发生变化。比较器将Uout与零相比较，实时检测Uout极性。FPGA接收比较器输出信号，在时钟信号下控制电子开关接通与Uout同相的反馈恒流源，使Uout减小至过零，再接通另外一相反馈恒流源，电路重复上述工作。对两相反馈基准恒流源的接通周期分别计数，2个计数值的差值即为电路的基础读数。

将反馈恒流源在一个时钟周期提供的电荷称为一个量化电荷。在积分器中，总有小于一个量化电荷的残余电荷不能被平衡。因此，使用A/D芯片对Uout进行采样，2次采样的差值为残余读数。将其与基础读数进行整合，即可得到电路的输出数字量。

根据电荷平衡原理，可以得到：

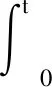
(1)

式中：Qin为Iin输入的电荷量；Nbase为电路基础读数；T为时钟周期；IrefT即为一个量化电荷Qref；CI为积分电容；UresCI即为残余电荷Qres；Ures为残余电压。

图1 高分辨率模数转换电路原理框图

1.2 积分环节

积分器是电路的采样保持环节，作用是采集输入电流，将结果以电荷形式存储在积分电容上，再经后级电路量化处理后转换成数字量。积分器的原理如图2所示。

图2 积分器电路原理图

积分器输出电压与输入电流的关系为

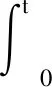
(2)

式中：Is为反馈电流，有±Iref2种取值。

1.3 量化过程

电路的量化过程由比较器、FPGA、电子开关及恒流源共同实现。比较器实时检测Uout极性，FPGA接收比较器输出信号，并控制电子开关接通正负两相恒流源，使Uout在零值上下波动。图3、图4、图5分别为输入电流Iin=0、Iin>0、Iin<0时的电路工作波形图。图中波形从上至下依次为：时钟脉冲、积分器输出电压、正相恒流源控制信号、负相恒流源控制信号。

图3 Iin=0时电路工作波形图

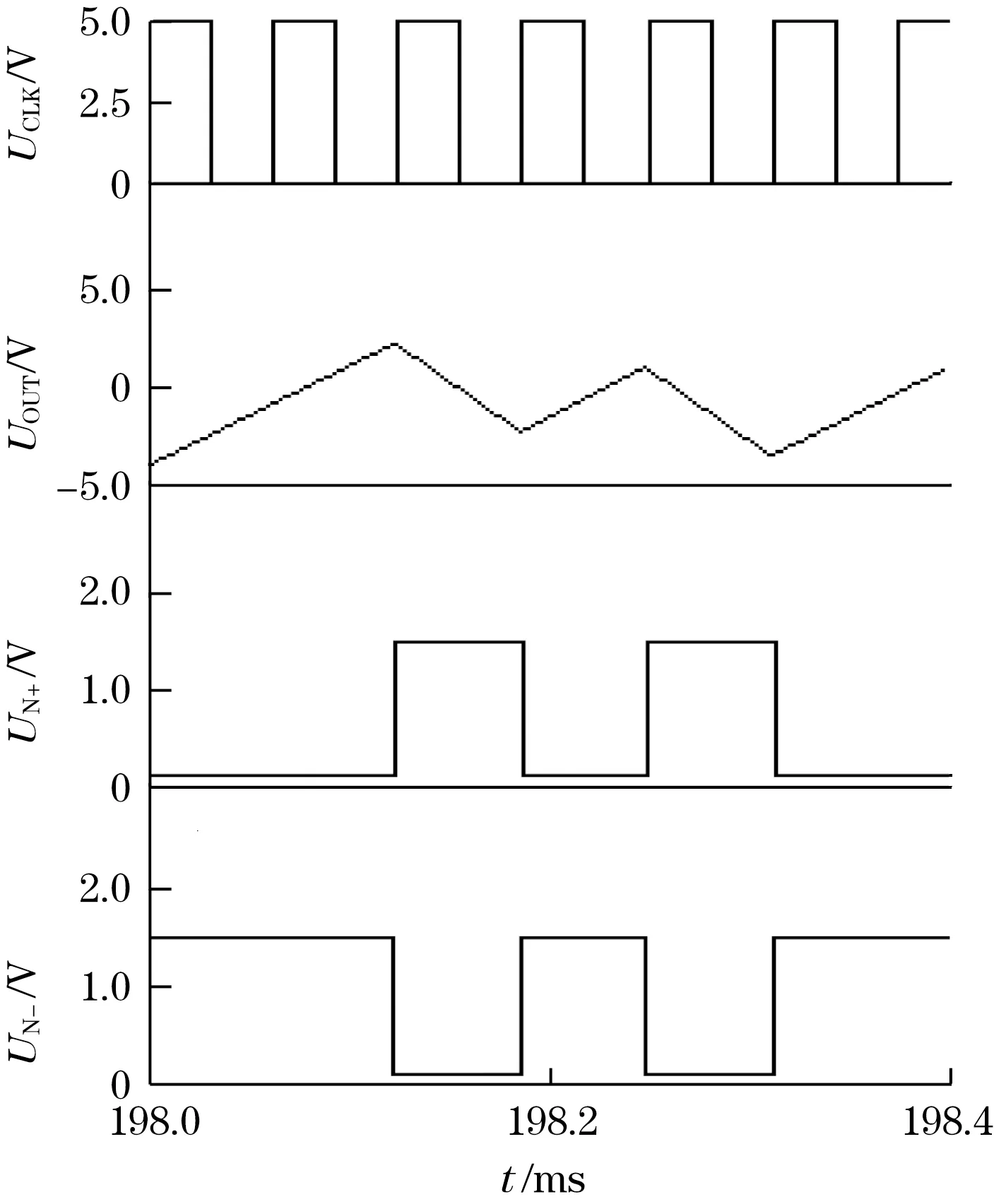
图4 Iin>0时电路工作波形图

图5 Iin<0工作波形图

当输入电流Iin=0时，正负相恒流源交替接通，设正相恒流源导通周期数为N+，负相恒流源导通周期数为N-，Nbase=N+-N-=0，基础读数为零。当输入信号Iin>0时，Nbase=N+-N-<0，基础读数小于零。当输入信号Iin<0时，Nbase=N+-N->0，基础读数大于零。

1.4 A/D采样电路

根据对电路工作原理的分析，A/D采样电路的作用就是读出残余电荷Qres。

设A/D采样芯片的位数为N。由于输入电流和反馈电流同时流入电路，则在1个时钟周期引起的Uout的最大变化为2Uref，Uref=Qref/CI，称为一个量化电压。设置A/D采样电路参考电压为±2Uref。则残余电荷对应的电路残余读数值为

(3)

由于一个量化电荷引起的电压变化为Uref，电路的输出数字量为

Nout=2N-2·Nbase+NAD

(4)

2 软件设计

电路的软件部分由FPGA和DSP共同实现。FPGA用来控制电路逻辑，包括电子开关、A/D采样和数据处理的逻辑控制。DSP用来将基础读数和残余读数进行整合及滤波处理，得到电路的输出数字量。

2.1 逻辑控制芯片FPGA

FPGA接收比较器输出信号，判断Uout极性，控制电子开关接通相应恒流源，对恒流源的接通周期进行计数，得到Nbase。同时，控制A/D芯片进行采样，控制DSP芯片进行数据处理。FPGA的设计模块如图6所示。

图6 FPGA设计模块

2.2 数据处理芯片DSP

DSP具有强大的数据处理功能，能够快速完成数据的整合和滤波。在FPGA控制下，DSP首先接收基础读数Nbase，然后读取残余读数NAD，之后对二者进行整合及滤波，得到高分辨率模数转换电路的输出数字量Nout。DSP的软件流程图如图7所示。

图7 DSP软件流程图

3 实验验证

根据原理图搭建电路，在常温下对电路进行测试。I/F转换频率为fIF=32 kHz，A/D采样频率为fAD=1 kHz，A/D采样芯片位数为16位。输入电流范围为-35～+35 mA。

3.1 电路满度输出

电路的满度输出是电路输入最大电流时输出的数字量。电路的满度输出取决于 I/F转换频率和A/D芯片位数。I/F电路的最大输出与转换频率相同，为3.2×104s-1。由于A/D转换引入了高频误差，只保留转换结果高M位有效，则电路的满度输出为fIF×2M。取M=5，满度输出数字量为1.024×106s-1。

3.2 零位

模数转换电路的零位偏置用来表示当输入信号为零时的输出数字量，可以通过软件进行补偿，但是无法完全消除。图8为电路每s输出数字量测试结果。计算得到电路的零位偏置为7.04 s-1。

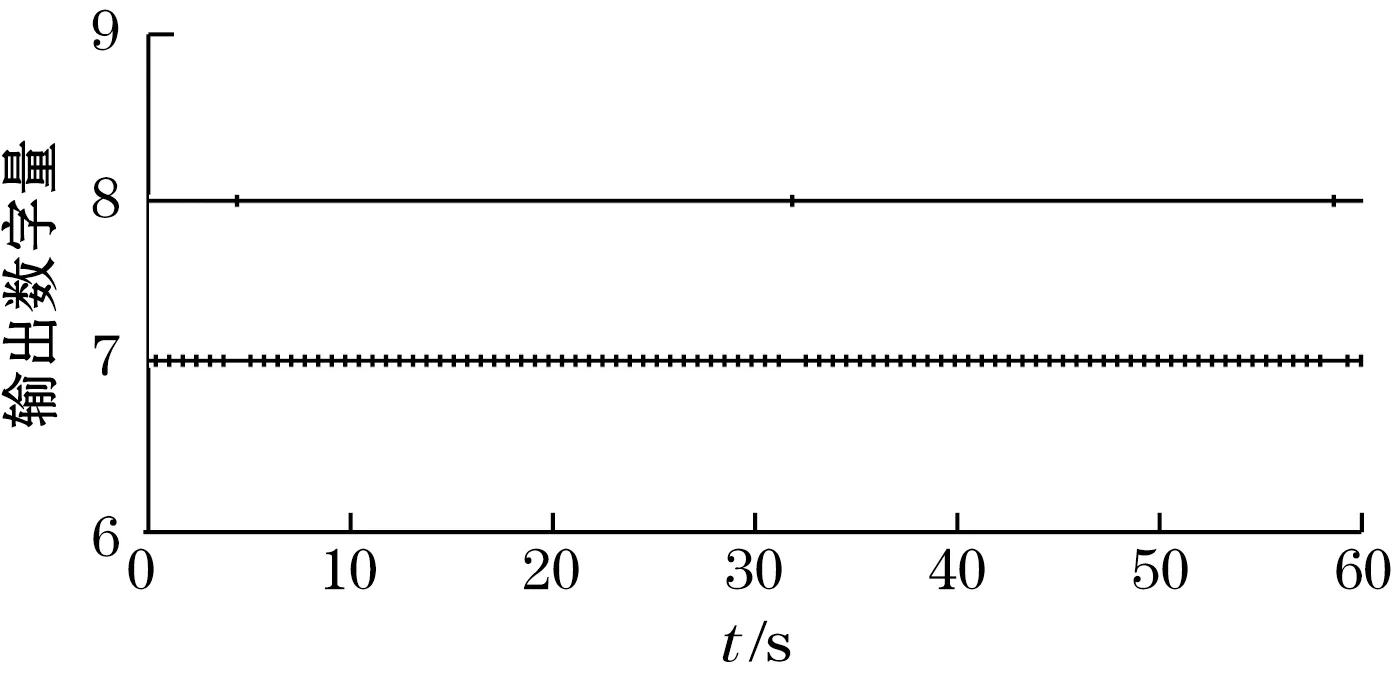
图8 零位偏置测试结果

3.3 标度因数

电路的标度因数K用来表示每s每mA电流的输出数字量，单位为(s·mA)-1。

在相同参数条件下分别输入±1 mA电流对电路进行多次测试，采样100 s数据，计算得到每s输出数字量，结果如表1所示。

表1 电路标度因数测试结果

计算得到高分辨率模数转换电路的标度因数为K=29 260.51 (s·mA)-1。

电路工作稳定后，通入+1 mA电流，测试电路的标度因数稳定性，每10 s记录电路的输出数字量，结果如图9所示。计算得到电路的稳定性为5.32×10-6。

图9 标度因数稳定性测试结果

3.4 线性度及对称性

电路的线性度用来描述输出数字量与输入电流之间的偏离程度。传统的I/F电路输出脉冲不均匀，识别小信号需要在时间上进行积累，电路的线性度较差。电路的对称性用来表征正负两个极性输出数字量的对称特性。

取9个采样电流值测试电路的线性度和对称性，采样时间为100 s，计算得到每s脉冲输出。测试结果如表2所示。

表2 电路线性度和对称性测试结果

计算得到电路的线性度为5.23×10-6，对称性为3.34×10-5。

4 滤波处理

为了消除硬件电路和A/D采样引入的高频误差，使用DSP芯片对输出数据进行FIR滤波，以对输出数字量进行平滑处理。

FIR滤波的输出只与当前时刻和之前时刻的输入信号有关，与输出信号无关，且FIR滤波器的冲激响应序列是有限长的，因此滤波器一定是稳定的[10]。由于DSP芯片强大的数据处理功能，使用DSP来实现FIR滤波几乎不会影响系统的实时性。

使用MATLAB软件的FDATool工具箱生成FIR滤波器。选取FIR滤波器的阶数为10阶。采样频率为Fs=1 kHz，设置通带频率Fpass=80 Hz，阻带频率Fstop=100 Hz，通带波纹Ap=3 dB，阻带衰减As=60 dB，得到滤波参数为

(5)

直接将得到的参数输入DSP中的FIR滤波程序。输入+1 mA电流对进行测试。滤波前后的每ms数字量输出如图10所示。

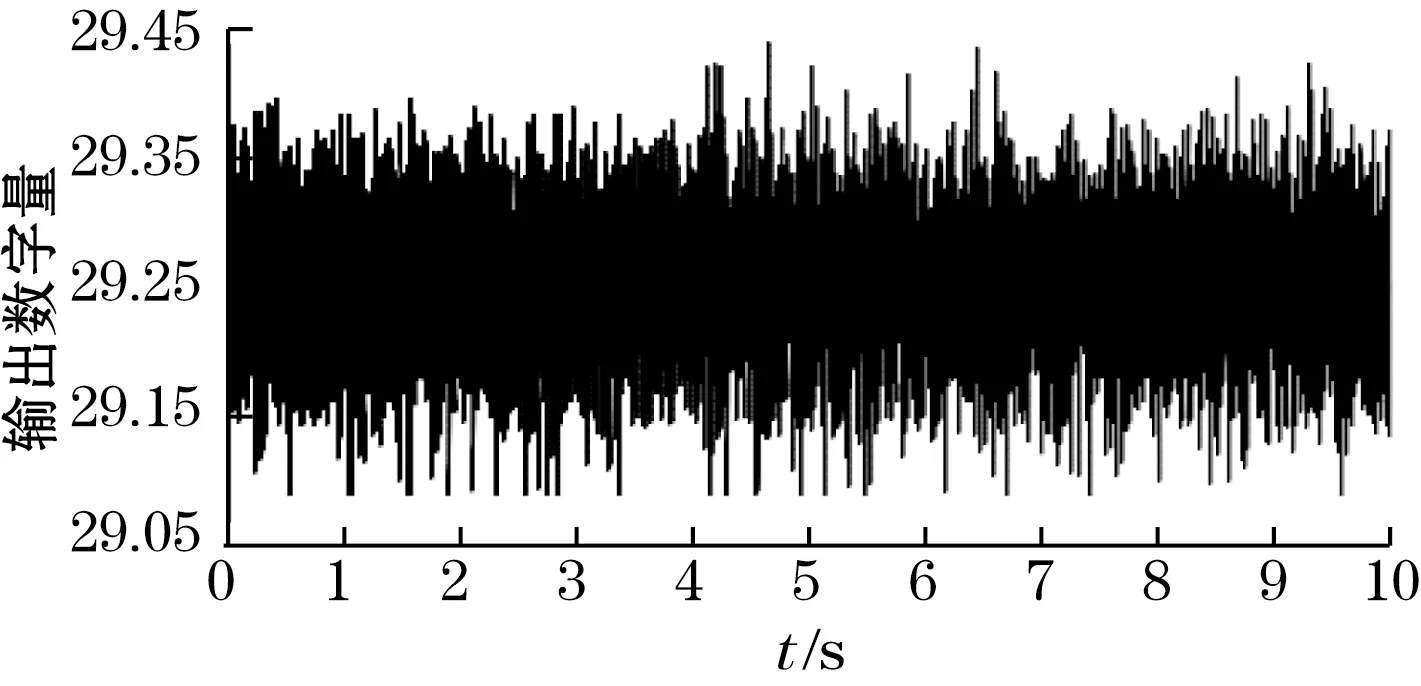
(a)滤波前

(b)滤波后图10 滤波前后每ms输出数字量比较

可以看出，FIR滤波后的输出数字量更为平滑，在不影响精度的前提下提高了稳定性，有效减小了高频误差带来的影响。

5 结束语

本文设计了一种高分辨率模数转换电路。将传统的电流频率转换电路和A/D采样芯片相结合，使用FPGA进行逻辑控制，减少分立器件的使用，增强了电路的可靠性，使用DSP进行数据处理，提高了电路的运算速度。经实验验证，在给定参数条件下，电路的满度输出数字量为1.024×106s-1，标度因数为K=29 260.51 (s·mA)-1，标度因数稳定性为5.32×10-6，零位偏置为7.04 s-1，线性度为5.23×10-6，对称性为3.34×10-5，在不影响电路精度和稳定性的前提下，同时满足了高分辨率和大量程的需求。

为了消除硬件电路和A/D采样引入的高频随机误差，基于DSP强大的数据处理能力，对电路的输出数字量进行了FIR滤波。使用MATLAB软件生成滤波参数后输入到DSP程序。实验结果表明，FIR滤波能够在不影响系统精度的前提下对输出的数字量进行平滑，有效消除电路引入的高频随机误差的干扰，增加了系统的稳定性。