二衬厚度对盾构隧道双层衬砌纵向力学性能的影响

2020-02-26郭文琦王士民杨赛舟

铁道标准设计 2020年2期

郭文琦,陈健,王士民,杨赛舟,4

(1.西南交通大学交通隧道工程教育部重点实验室,成都 610031； 2.中国海洋大学环境科学与工程学院,山东青岛 266003； 3.中铁十四局集团有限公司,济南 250101； 4.中国建筑西南设计研究院有限公司,成都 610041)

近年来，随着盾构技术的发展，盾构法已成为目前地下轨道交通建设的主流方法[1-3]。同时，盾构隧道由于纵向不均匀变形而出现的渗水漏泥、管片接头处张开等病害问题日渐突出[4]，因此研究隧道纵向力学性能有重要意义。

学者们对盾构隧道纵向不均匀变形进行了一系列研究。黄宏伟[4]等对软土盾构隧道纵向变形和结构性态进行讨论，重点分析了土性不均匀与荷载变化两大主要因素对隧道纵向变形的影响。李春良[5]等基于弹性地基梁理论，建立了地面荷载作用下的盾构隧道结构的纵向内力模型，该模型能预测出地面集中荷载或均布荷载作用时地下盾构隧道产生的纵向附加沉降变形和内力。苏道振[6]通过建立三维的盾构隧道模型的方法，采用32环管片，分析研究了不均匀沉降对盾构隧道管片受力的影响。李鹏[7]等在修正的等效连续模型基础之上对纵向弯曲造成的越江隧道不均匀沉降的控制指标值进行了研究，并针对环向错台造成的越江隧道纵向不均匀沉降，研究了相对弯曲的合理取值。殷建国等[8]通过建立盾构隧道纵向等效连续化的模型，分别对于纵向等效刚度为常数以及纵向等效刚度沿隧道纵向变化的情况，研究了隧道纵向沉降对盾构隧道纵向等效刚度的影响。李春良等[9]通过建立复杂地质条件下盾构隧道的纵向力学模型，研究了纵向刚度变化下隧道的力学性能。苏宗贤等[10]通过纵向壳-弹簧-接触模型，采用强制位移法得到的结果表明，盾构隧道的纵向变形不但会产生纵向附加内力，还会产生一定量的横断面变形和横向附加内力。

对于盾构隧道纵向不均匀变形的分析，既有隧道纵向力学性能的研究对象集中于单层衬砌结构，鲜有盾构隧道双层衬砌纵向力学特性的相关研究报道。鉴于此，为了真实地模拟隧道纵向非连续特征并对盾构隧道双层衬砌纵向力学性能进行研究，以武汉地铁8号线越江隧道工程为依托，建立双层衬砌盾构隧道的纵向三维模型，研究不同二次衬砌厚度对隧道纵向弯曲刚度和纵向不均匀变形的影响。

1 工程概况

武汉地铁8号线越江隧道是目前国内直径最大的单管双线地铁盾构隧道，同时该隧道也是国内首座全线敷设二次衬砌的地铁盾构隧道。该隧道全长3 186 m，采用直径为12.54 m的泥水平衡式盾构，盾构区间示意见图1。

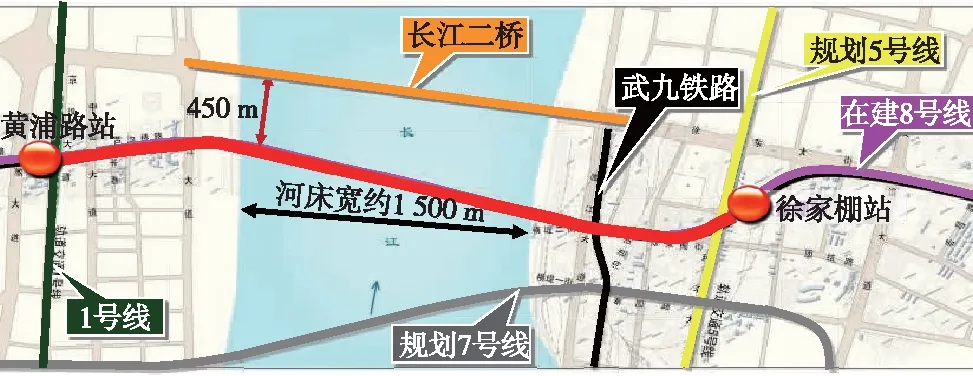
图1 盾构隧道区间平面示意

武汉地铁8号线越江隧道外径为12.1 m，内径为10.5 m，壁厚为0.5 m，管片的幅宽为2 m，管片采用强度等级C50的混凝土，管片的分块模式为 “5+2+1”，即每环衬砌由5块标准块、2块邻接块和1块封顶块拼装而成。隧道横断面形式如图2所示。

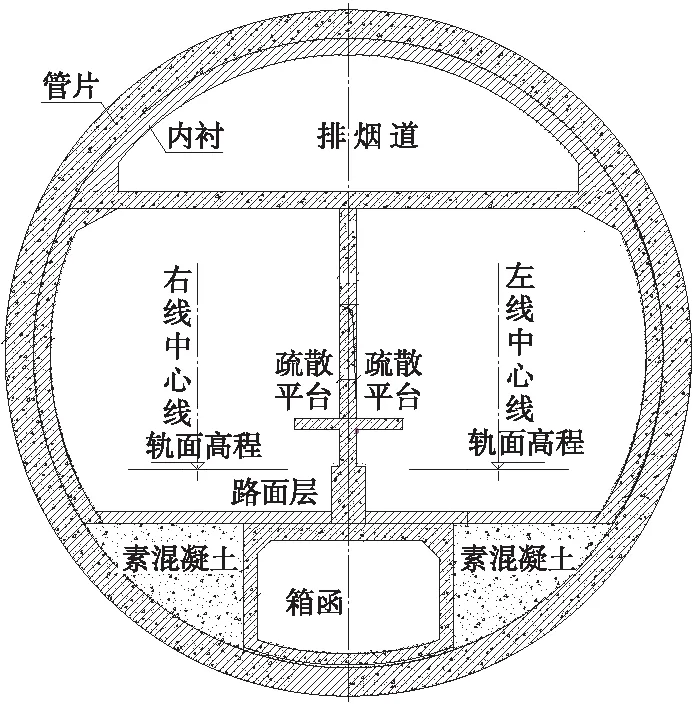
图2 隧道断面构造

武汉地铁8号线越江隧道工程所处地区的地质纵断面如图3所示。沿隧道纵向可将隧道所穿越的地层分为3部分：汉口段、过江段和武昌段。其中，过江段和武昌段的地层软硬不均现象较为明显。例如，在过江段AK10+380以南，隧道穿越上部为圆砾土、下部为砾岩的复合地层，在武昌段AK11+700以北，隧道需穿越上部为中粗砂、下部为砾岩的复合地层。

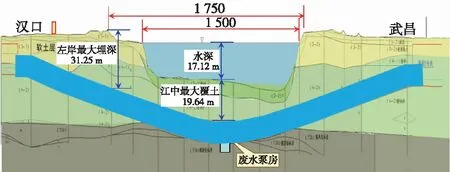
图3 越江段地质纵断面(单位：m)

这两种复合地层的软硬和密实程度相差较大，容易使得隧道的纵向受力特性发生突变，如出现较大的纵向不均匀沉降或出现内力分布集中的问题，导致隧道出现漏水和管片开裂等病害，对隧道的健康构成严重的威胁。因此，研究盾构隧道纵向力学特性具有重要意义。

2 数值计算模型

2.1 模型概述

针对现有的计算模型存在的不足，结合工程实际，本研究基于考虑盾构隧道环、纵向接缝盾构隧道双层衬砌三维壳-弹簧模型[12]，建立纵向19环管片长度(38 m)的盾构隧道双层衬砌三维纵向模型，并进行纵向力学性能分析。数值计算模型如图4所示。

图4 双层衬砌纵向三维模型

2.2 数值计算模型参数

在该模型中，管片及二次衬砌采用具有一定厚度的壳单元模拟[12]，该单元为4节点塑性大应变单元，可以合理地模拟衬砌结构的力学性能。管片及二次衬砌参数取值如表1所示。

表1 管片及二次衬砌参数

参考既有的分析研究以及工程实例[13-14]，结合该隧道工程的管片厚度和螺栓的强度(3M36)，从而计算确定数值模型中的抗弯刚度。对于管片与二次衬砌的接触，该接触面采用切向弹簧单元和仅受压的杆单元，按照串联弹簧刚度计算公式确定其压缩刚度和剪切刚度[12]。相关参数取值如表2所示。

表2 刚度取值 N·m/rad

3 纵向等效弯曲刚度的影响分析

学者们对盾构隧道的纵向等效刚度进行了一系列研究。张文杰[15]等在考虑盾构隧道横向影响以及纵向环缝影响的基础上，提出了一种广义的纵向等效连续化模型。叶飞等[16]在纵向等效连续化模型的推导中引入横向弯曲刚度，得到了考虑横向刚度有效率的纵向等效抗弯刚度计算式。日本学者志波由纪夫认为，在隧道纵向可将由接头和管片组成的盾构隧道等效为具有相同刚度和结构特性的均匀连续梁[17]。基于该理论，通过比较单层管片衬砌结构、不同二衬厚度的双层衬砌结构的盾构隧道等效连续梁的弯曲刚度，探究二次衬砌厚度对双层衬砌盾构隧道纵向等效弯曲刚度的影响。

3.1 荷载及边界条件设定

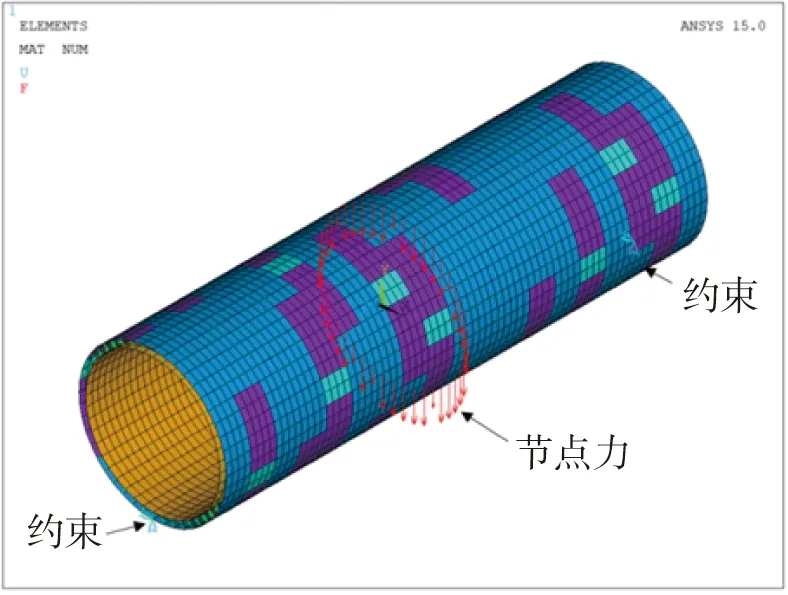
图5 跨中截面节点加载及两端约束情况

如图5所示，采取简支梁的受力模式，在隧道三维模型两端底部分别施加其X方向和Y方向的约束。本文计算中采用三维壳单元来模拟衬砌结构，把集中力P分解为等效的节点力施加于跨中截面节点上，如图5所示。

由材料力学的原理可知，当集中力P作用在简支梁的跨中截面时，其最大挠度为

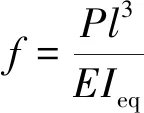
(1)

其中，本文计算中跨中截面的荷载P取100 kN，隧道纵向计算长度取为38 m。

3.2 计算结果分析

本文计算单层管片衬砌以及二次衬砌厚度为20～60 cm(每5 cm设置1个计算工况)的双层衬砌结构共10种情况，部分衬砌变形云图如图6所示。

图6 衬砌变形计算云图(单位：m)

不同二次衬砌厚度的双层衬砌隧道纵向等效弯曲刚度计算结果汇总如表3所示。

表3 纵向等效弯曲刚度汇总

由表3可以看出，施作二次衬砌后，隧道跨中最大挠度显著降低，等效弯曲刚度明显提升。当施作厚度为40 cm的二次衬砌后，隧道跨中截面最大挠度为0.93 mm，约为单层管片挠度值的46%；隧道的纵向等效弯曲刚度为5.88×1012N·m/rad，约为单层管片弯曲刚度值的2.2倍。由此可以看出，施作二次衬砌可显著提高隧道的纵向等效弯曲刚度，对隧道抵抗纵向变形的能力也有显著提升。

根据表3数据，绘制隧道纵向等效弯曲刚度随二次衬砌厚度变化曲线，如图7所示。

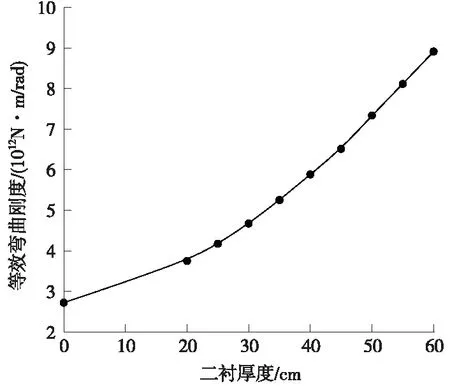
图7 纵向等效弯曲刚度随二次衬砌厚度变化曲线

由图7可以看出，隧道纵向等效弯曲刚度随着二次衬砌厚度的增大呈近似线性增大，对应的隧道整体抗弯性能越好。需要说明的是，增大二次衬砌的厚度可提高双层衬砌的隧道抵抗变形的能力，但仅通过提高二次衬砌厚度来减小隧道纵向变形的可行性有待进一步研究。

4 纵向变形条件下双层衬砌纵向力学性能分析

盾构隧道在纵向上会因不均匀变形而出现环缝张开量、错台量过大等现象，进而引发隧道渗水漏泥、结构局部破坏等病害，影响隧道的正常运营。

对于已经建成的隧道，一般很难测定其在长期营运过程中产生纵向变形的荷载值，而我们可以准确地测量出隧道发生的纵向变形，因此可采用强制位移法对隧道纵向变形进行研究[10-11]。基于已建立的盾构隧道双层衬砌纵向三维数值计算模型，以位移作为统一的等效荷载，分析不同二次衬砌厚度下隧道的纵向变形形态、附加内力分布。

本计算模型中的具体做法为：固定模型的一端(右端)，以位移作为强制荷载施加在模型的另一端(左端)，在左端加10 mm位移荷载。参照工程地质条件相似的武汉地铁2号线越江隧道纵向变形研究数据，隧道发生10 mm不均匀沉降时，其影响区域在38 m(19环管片长度)以内。

4.1 管片错台量分析

当二次衬砌厚度为30 mm时，双层衬砌结构纵向沉降云图如图8所示，为了观察结构的纵向变形形态，将位移放大300倍显示。

图8 二次衬砌厚度30 cm时结构纵向沉降云图(单位：m)

由图8可知，在左侧端部强制位移的作用下，隧道发生了一定程度的挠曲变形，沉降从左向右逐渐减小。在左侧第二环以及右侧第二环处管片接缝明显张开，说明该处的弯曲变形较大，对该处的线路平顺性有较不利影响。

为了更好地分析不同工况下线路的平顺性，将管片从左向右依次编号，并取每环管片幅宽中点处的沉降量绘制隧道纵向沉降曲线，如图9所示。

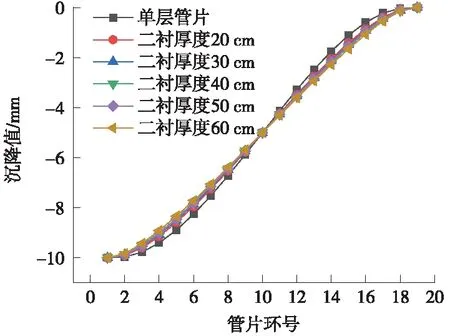
图9 不同二次衬砌厚度隧道纵向沉降曲线

由图9可知，不同二次衬砌厚度的盾构隧道发生的不均匀沉降在纵向上呈挠曲线形态，且以第10环管片为中心，前9环管片与后9环管片的挠曲形态接近反对称分布。比较前9环管片的隧道沉降曲线可知，在位移荷载作用下，单层管片的纵向沉降曲线的曲率最大，施作二次衬砌后，隧道沉降曲线曲率明显减小，且随着二次衬砌厚度的增大，隧道沉降曲线曲率继续减小。当二次衬砌厚度为60 mm时，第2环至18环管片之间的沉降曲线已接近直线。

管片的错台量为相邻管片沉降的差值，故管片错台量沿隧道纵向的分布函数可视为隧道沉降曲线的一阶导数，不同工况下管片的错台量纵向分布曲线如图10所示。

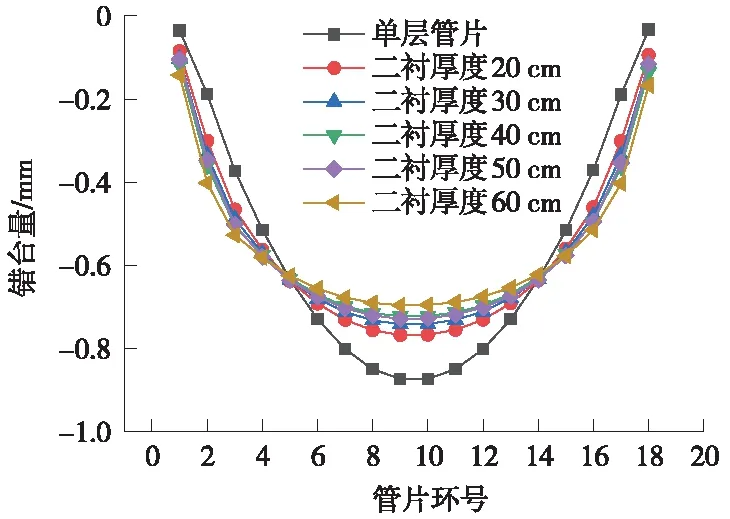
图10 不同二次衬砌厚度下管片错台量纵向分布曲线

由图10可知，对于不同的工况，错台量纵向分布曲线的规律基本一致：曲线总体呈二次抛物线型分布，对称轴位于中部第9～10环管片之间，隧道的错台量在该处取得最大值，并向两端逐渐减小。各工况的管片错台量曲线在第5环和第14环相交，在第5～14环之间，管片错台量随着二次衬砌厚度的增大而减小，而在第1～5环、第15～19环之间，管片错台量随着二次衬砌厚度的增大而增大。

由上述规律可知，二次衬砌对于降低隧道纵向中部不均匀变形是有利的，但对于隧道纵向两端的不均匀变形是不利的。有无施作二次衬砌对于错台量变化的影响明显大于二次衬砌厚度变化的影响。隧道中部是错台量峰值所在的部分，错台量值较大，在二次衬砌施作后，错台量峰值明显降低。因此，相对于单层管片衬砌来说，二次衬砌的施作在总体上明显提高了隧道抵抗纵向不均匀变形的能力。

4.2 管片环缝张开量分析

由图8可知，管片环缝在靠近施加位移荷载端和固定端附近产生了较为明显的张开现象。提取隧道纵向接头的环缝张开量，如图11所示，可知越靠近端部，管片的环缝张开量越大。

图11 管片环缝张开局部放大(单位：m)

为了进一步分析二次衬砌对管片环缝张开量的影响，取不同工况下双层衬砌管片环缝的最大张开量与单层衬砌管片的最大张开量进行比较，如表4所示，表中所示的增量为不同厚度双层衬砌管片环缝张开量相对单层衬砌管片环缝张开量的增量。

由表4可知，相对于单层衬砌，双层衬砌结构中管片的最大环缝张开量较大，且随着二次衬砌厚度的增加，管片环缝的张开量也随之增大。由此可见，二次衬砌厚度越大，隧道的环缝张开量越大，即靠近端部的变形越大。

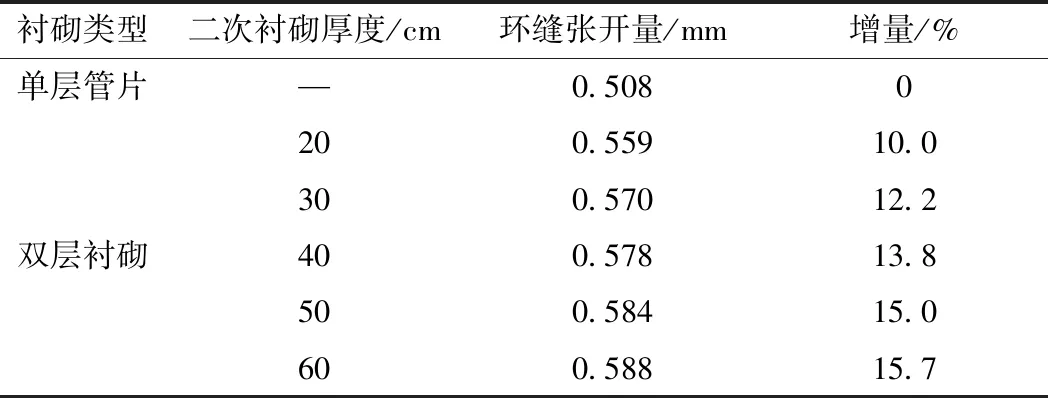
表4 管片环缝最大张开量

施作二次衬砌后结构的整体刚度有了明显的提高，在受到位移荷载作用时，靠近荷载作用和端部约束作用的位置处由于刚度较大而使得该处的局部内力和变形过大，局部的环缝张开量增大。

4.3 管片及二次衬砌纵向附加内力分析

在外部荷载的作用下，结构产生的变形与内力是互为表里、不可分割的，因此需对双层衬砌结构在纵向位移荷载的作用下结构中产生的附加内力进行分析。

考虑到剪力的量值较小，且本文主要分析结构的纵向性能，因此主要提取结构纵向的弯矩和轴力进行分析。单层衬砌纵向附加内力计算结果如图12所示，双层衬砌纵向附加内力计算结果(以二次衬砌厚度30 cm为例)如图13所示。

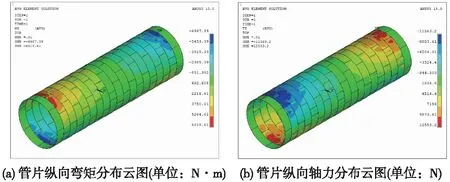
图12 单层衬砌纵向附加内力

图13 双层衬砌纵向附加内力(二衬厚度30 cm)

对比图12和图13的内力计算结果可知，在位移荷载作用下，单层衬砌结构和双层衬砌结构的内力分布规律一致，都表现为两端内力异号，且量值最大，由两端向中间逐渐减小的趋势。相对于单层衬砌管片，双层衬砌结构所受的内力有明显增大，且增量主要集中在管片上，管片所受的弯矩从6 987.39 N·m增大至13 824.5 N·m，增大了97.8%，轴力从11 563.2 N增大至23 335.7 N，增大了101.8%。二次衬砌也发挥了一定的承载作用，其承受的内力约为管片的20%左右。

通过比较内力和变形的计算结果可知，内力的分布与变形规律相互关联，在管片的弯矩和轴力分布曲线中，纵向模型两端的弯矩、轴力峰值所在部位即为环缝张开量最大的区域。此外，单层管片的内力从两侧向中间减小的趋势较为平缓，而双层衬砌管片的内力在两端迅速减小，中间部分的内力已衰减到较小的量值且保持基本不变，这与前述研究得到的纵向沉降曲线变化规律是一致的。因此，相对于单层衬砌而言，双层衬砌结构刚度较大，在位移荷载作用点部位产生了明显较大的内力，并导致该部位的变形较大，而对于隧道的其他部位影响较小。

为了进一步探究二次衬砌厚度对于双层衬砌结构内力的影响，提取不同工况下的内力计算最值进行比较分析。由于二次衬砌所承担内力量值较小[18-21]，且管片的内力最大值与最小值的绝对值量值接近，因此本处仅对管片的最大内力值进行分析。不同二次衬砌厚度的结构内力计算结果如表5所示。

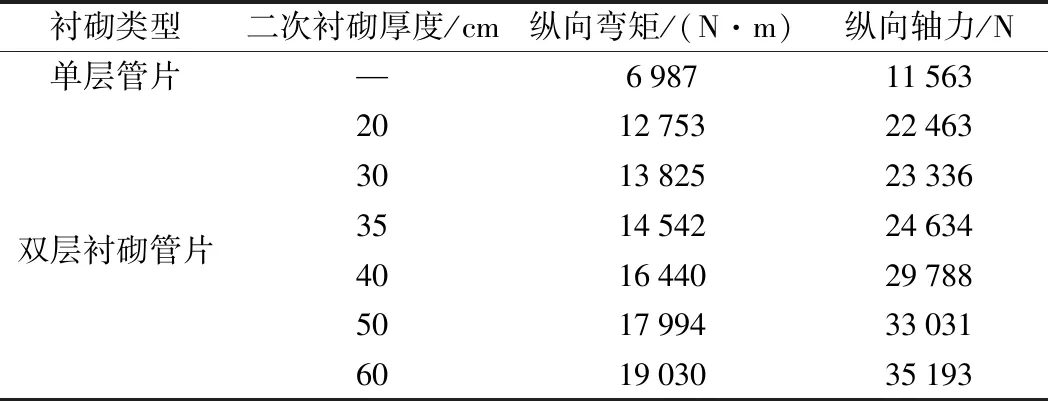
表5 管片纵向附加内力最值计算结果

由表5可知，随着二衬厚度的增大，双层衬砌结构管片所受到的内力逐渐增大。当二次衬砌厚度达到60 cm时，双层衬砌管片所受到的附加弯矩达到单层衬砌管片的272%，附加轴力为单层衬砌管片的304%，内力随厚度增大的效果较为明显，这与管片环最大接缝张开量的规律是一致的。

根据表5中的数据，绘制管片纵向附加内力随二次衬砌厚度变化曲线，如图14所示。

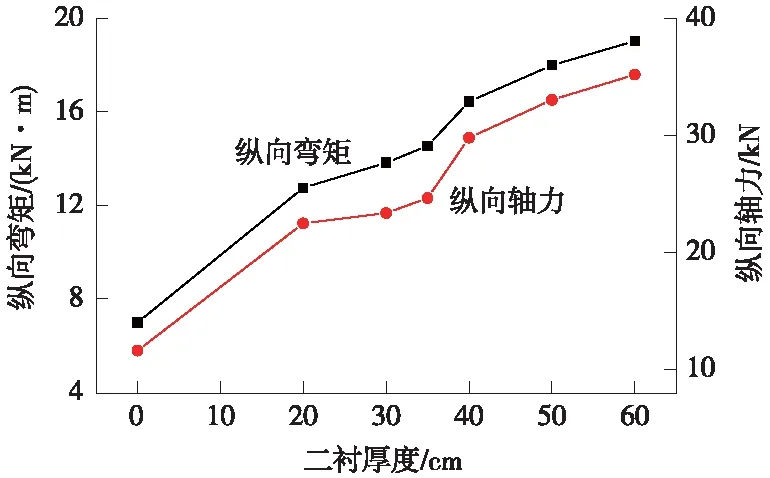
图14 管片纵向附加内力随二次衬砌厚度变化曲线

从图14可以看出，随着二次衬砌厚度的增大，双层衬砌结构管片所受到的轴力和弯矩逐渐增大，二者在二衬厚度为20～35 cm时增加幅度较小，当二衬厚度达到35 cm以后，管片所受到的轴力和弯矩突增，这说明在二衬厚度为20～35 cm时，管片与二次衬砌两者间的相互作用效果较好，管片所受到的纵向附加内力较小。同时综合考虑工程造价和二衬是否设置配筋的问题，二衬厚度取20～35 cm是较为合理的。