钢管混凝土桁架Y型管节点热点应力研究

2020-02-26温宗意刘铭扬吕明达

铁道标准设计 2020年2期

卫星,温宗意,肖林,刘铭扬,吕明达

(西南交通大学土木工程学院桥梁工程系,成都 610031)

钢管桁架结构广泛用于桥梁、海洋平台、通信塔等结构物中，在钢管中填充混凝土形成钢管混凝土结构，更是我国大跨度拱桥设计的首选[1]。这些结构在服役期间，总是承受着不同程度的循环荷载，其中采用钢管混凝土桁架的桥梁结构长期承受车辆荷载反复作用，近几年，在国内已建成的钢管混凝土桁架桥梁中疲劳问题日渐凸显[2]。这对钢管混凝土桁架结构桥梁的设计、运营管养及性能评价带来了新的问题。

焊接管节点是钢管桁架结构桥梁承载的重要部位，也是容易发生疲劳开裂的薄弱部位。基于热点应力的S-N方法在复杂性和精确性上做到了很好的平衡[3]，已在海洋平台等结构疲劳设计中得到应用，国际上对于应用热点应力法进行焊接节点疲劳性能评估得到了大力的推荐。应力集中对于焊接构件的疲劳行为十分重要，研究沿焊趾的应力集中系数(SCF)分布是研究钢管混凝土(CFST)管节点疲劳受力行为必不可少的[4-6]。引入热点应力作为疲劳设计时的参考量，以热点应力法研究，对于空钢管连接的管结构形式，国内外学者介绍了很多的试验和数值模拟公式[7-12]，这些公式通常由关于管节点几何特点的无量纲关系(管径比，径长比，壁厚比等)构成函数，展示了不同节点形式的热点应力分布情况。

对于主管填充混凝土，支管为空钢管的钢管混凝土节点构造形式的SCF研究相比空钢管节点还不够充分。国内外学者做了试验和数值分析[13-19]，主要都集中于T，Y型节点，通过改变构造尺寸进行研究以及掌握SCF分布特点，对于特定的节点构造形式提出了由数值试验拟合的无量纲公式。同时对于焊缝的构造细节进行了深入探讨，这在对空钢管研究时常常是被忽略的一个因素。

支管承受荷载时，往往主管会发生整体弯曲和径向的变形，主管向支管提供了一个弹性支撑。当主管内填混凝土后，约束增强，提高了整体、局部刚度，因此应力集中系数较空钢管情况而言得到了很大改善，SCF整体下降，热点应力极值点位置发生了改变，依靠空钢管节点的变化规律来判断CFST管节点的应力分布情况有时并不符合实际。在所述文献中，尽管有对于Y型节点的研究，但是根据钢管夹角变化没有进行独立研究，以及支撑条件改变引起的SCF分布变化没有探讨。本文建立支管不同角度，不同约束的Y、T型CFST管节点模型，支管受轴压作用，采用国际管结构发展与研究委员会(CIDECT)建议的热点应力的基本理论和方法[7]，研究模型相贯线上焊趾的SCF分布情况，并分析比较SCF最大值位置，以及数值的变化趋势，讨论变化情况，得出规律性结果。

1 热点应力基本外推方法

焊接节点焊趾处应力具有高度的非线性，如图1所示，热点应力是结构应力(也称几何应力)的最大值，结构应力是构件薄膜应力与弯曲应力的组合应力。计算热点应力的方法是不受切口效应影响时，沿构件表面进行插值外推(线性，或二次)，所以热点应力实际是人为指定的一种应力，并不是某一特定位置的应力。根据国际钢管结构发展与研究委员会CIDECT提出的方法，进行有限元计算热点应力时，可采用如下规定计算热点应力值：以线性外推时，距离焊趾0.4t，1.0t的位置提取应力值，按照式(1)，得出热点应力σhs；二次外推为，距离焊趾0.4t，0.9t，1.4t的位置提取应力值，按照式(2)，得出热点应力σhs。其中t为管壁厚。

σhs=1.67σ0.4t-0.67σ1.0t

(1)

σhs=2.52σ0.4t-2.24σ0.9t+0.72σ1.4t

(2)

选取垂直于焊趾方向热点正应力更适合焊接管节点疲劳分析。因为管节点的疲劳破坏主要是随着焊缝处表面裂纹的萌生和扩展产生的，因此垂直于该裂纹方向的应力对裂纹的扩展起主要作用，同时，区别于最大主应力(第一主应力)，垂直焊趾方向的正应力无需考虑外力的作用方向，可以进行线性叠加，且易于测试，操作步骤明确。

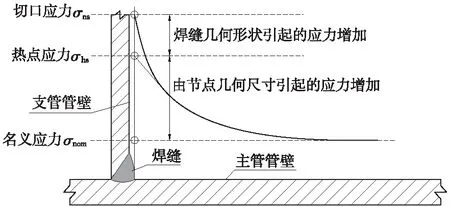
图1 焊趾处应力分布

在管节点疲劳破坏的研究中，热点应力集中系数(SCF)是评价其疲劳性能的重要参数，同时便于体现应力的不均匀特性和应力集中程度，以及设计与研究使用，因此本文热点应力计算结果均以SCF表示，表达式见式(3)，通过对热点应力集中系数的研究反应热点应力的分布情况。由童乐为等[15]验证，所有热点应力SCF取值，按照主管采用线性外推确定，支管采用二次外推取值。σnom名义应力即为梁单元平均应力，支管受轴压作用下，名义应力见式(4)。其中，主管取管壁外表面沿垂直焊缝方向正应力，支管取支管外表面沿支管轴线方向正应力。

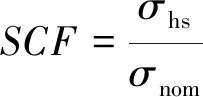
(3)

(4)

式中D——支管外直径；

d——支管内直径；

FN——支管轴力。

2 有限元模型建立与验证

2.1 模型建立

利用有限元软件ANSYS，采用20节点实体单元建立CFST三维实体模型，并模拟焊缝。几何模型如图2所示，有限元模型如图3所示。内填混凝土材料参数为C50混凝土参数，建模时，假定混凝土与钢管之间黏结。

角度变化时，支管轴线始终与主管轴线中点相交，一端固定，一端铰接情况下，为左端固结，支管偏向侧为滑动支座；两端铰接情况下，为左端固定铰支座，支管偏向侧滑动铰支座；两端固定即两端均为固结支座。

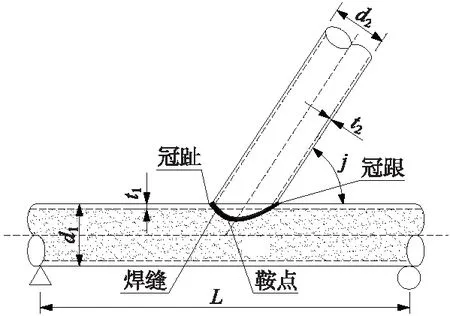
图2 几何模型示意

图3 有限元模型

几何无量纲参数表达式分别见式(5)，其中，d1、d2分别为主管和支管的外直径，t1、t2分别为主管和支管的壁厚，L为主管计算长度。

(5)

有限元模型在建立时，设置外推区域，外推范围内单元设定按热点应力公式要求，确保在需要的位置处存在节点，便于采集数据，计算热点应力。

2.2 模型验证

根据文献[20]中轴压试验，建立支管受压有限元模型对比试验结果，以验证有限元模型的可靠性。边界条件为两端铰接，几何参数见表 1。

主、支管有限元模型计算结果与实际结果对比见表2。从支管底部向上看，以相贯线轮廓平面投影的冠点连线和鞍点连线为坐标，连线交点为圆心，设定角度，具体见图4，其中0°为冠点，90°为鞍点。

表1 无量纲参数

表2 热点应力集中系数结果对比

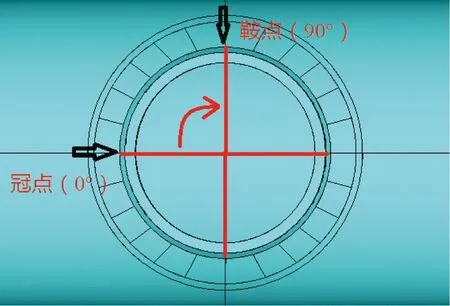
图4 方向示意

从表2可以看出，支管最大相差约23%，发生在支管鞍点，主管最大相差约30%，发生在主管鞍点。主管有限元结果较试验数据偏小，支管有限元结果较试验数据偏大。有限元计算结果与试验结果对比下，热点应力集中系数最大值均处在主管冠点，最小值处在主管鞍点，分布趋势相同。

当支管承受荷载时，荷载传递到相贯线后，由于相贯部分的空间性，在主、支管相贯线的各部位表现为刚度的分配不均，从而产生了起伏变化的SCF分布。对于有限元模型，主管内混凝土与主管粘结，支管承压后，主管产生面外的径向变形也受到了混凝土的面外约束(试验状态下，这种粘结可能很容易就失效，混凝土与外钢管变形不一致)，主管相贯线上的计算值在膜应力与弯曲应力的叠加下，产生了较试验值小的结果；同时，由于主管连接部分可以看作是支管与主管的多点弹性支撑，在混凝土的横向约束下，刚度较实际试验情况较大，因此支管计算数值较试验结果大。

可见支管承受轴压时，受到主管径向变形特点的影响，计算结果与试验结果总是在主管、支管鞍点部位差异最大。

考虑到焊缝尺寸不能够精确模拟，边界条件达不到理想状态，混凝土可能发生部分脱空等问题，部分位置结果存在较大的差异，但是，从结果来看可以认为数值模型可以反应热点应力分布趋势，具有一定的可靠性。

3 计算结果分析

3.1 相同约束随角度变化情况

图5为主管一端固定，一端铰接时，支管角度由20°向90°变化时，管节点沿焊缝焊趾SCF变化情况。图6为主管两端固定时，支管角度由20°向90°变化时，管节点沿焊缝焊趾SCF变化情况。图7为主管两端铰接时，支管角度由20°向90°变化时，管节点沿焊缝焊趾SCF变化情况。

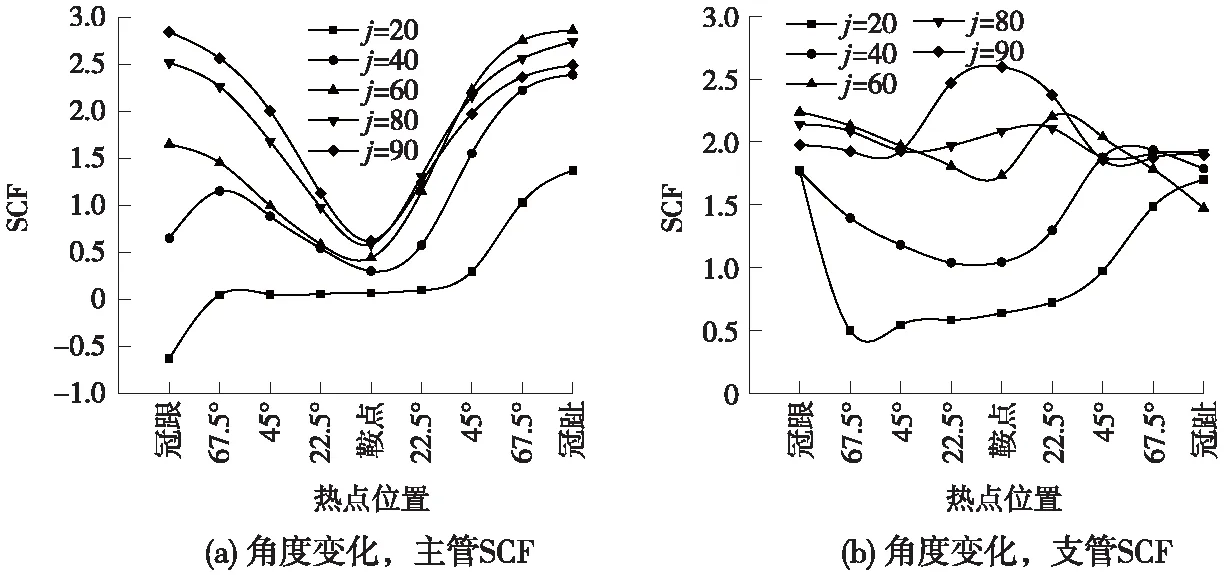
图5 一端固定，一端铰接

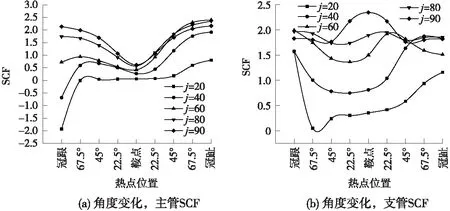
图6 两端固定

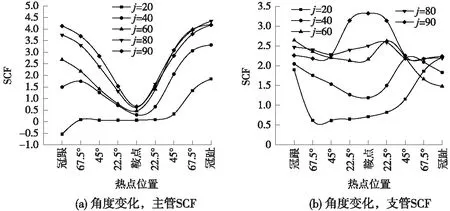
图7 两端铰接

一端固定，一端铰接时，管节点大角度侧相贯线即冠跟到鞍点之间，主管热点应力分布随角度增大而增大，变化明显；鞍点到冠趾之间，主管SCF在角度由20°到60°变化时，逐渐增大，60°时，达到顶峰并在80°，90°时有所下降，最大由2.8下降到2.5，变化幅度不大，除90°外，其余情况SCF极大值总是处在冠趾位置，极小值始终停留在鞍点位置。支管在角度变化下，热点应力最大值由冠趾向鞍点移动，且主管SCF普遍高于支管。j=90°时，支管轴向力沿主管的分量为零，按梁单元理论，由于支座条件，冠趾处引起沿焊缝方向正应力的弯矩相较于冠跟处小，最大热点应力集中系数发生在冠跟处。

角度在40°～80°时，两端约束不同导致外力水平分量引起的应力水平在鞍点两侧不同，在鞍点到冠趾处引起应力叠加，所以高于冠跟到鞍点段；主管填充了混凝土，径向刚度较空钢管增大，与空钢管鞍点处热点应力较大的情况不同，相贯线局部変形时两冠点处较鞍点处凹凸程度更大，因此主管冠趾处，膜应力和弯曲应力的正向叠加，导致热点应力最大点始终发生在冠趾处。角度为20°时，外力水平分力影响占主要地位，局部变形导致冠跟附近与冠趾附近变形相反，虽然从图中看冠跟附近变化区域小，SCF下降的很快，但是由于相贯线投影此时像一个鸡蛋状，冠跟附近变化区域的弧长是要大于冠趾处影响区域。

图6、图7与图5数值不同，但SCF分布趋势基本相同。随角度变化时，支管最大热点应力集中系数所在位置由冠点(冠趾)处向鞍点移动；80°时，相贯线上热点应力集中系数分布较为均匀。与主管变化的内凹的趋势不同，支管变化呈现外凸的趋势，所以主支管相贯线上的局部变形形状是不一样的。

可以看出，总体上，沿相贯线主、支管SCF的分布是随着角度的增大而增大的；除角度为20°外，热点应力集中系数最大值始终发生在主管，且主管冠点是危险位置；角度达到60°之后，主管SCF最大值变化不大；支管最大热点应力集中系数最大值随角度变化，由冠点向鞍点移动。

3.2 相同角度随约束变化情况

角度相同时，主管上沿焊缝SCF随约束变化情况如图8所示。

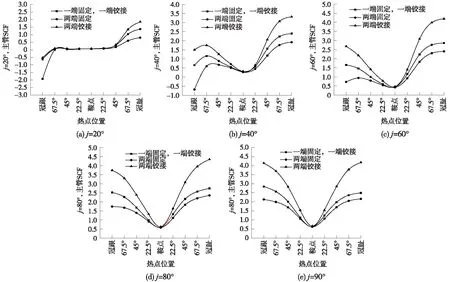
图8 主管SCF变化情况

总体来看，约束不同不影响主管热点应力的分布情况，只改变主管热点应力数值大小，角度变化在40°～90°时随着主管两端约束的加强，热点应力集中系数明显减小，两端固结时，热点应力集中系数最小，随着角度变化时，弯曲作用增强，两端约束越强，主管弯矩越小；角度为20°时，两端固定时冠跟距主管焊缝上67.5°测点之间，主管轴向分力压力引起的拉应力作用明显，弯曲作用较小，出现负的热点应力集中系数；除角度为20°时情况，其他角度下，鞍点附近随约束变化较小，可以看出两端约束变化对于主管垂直于焊缝鞍点处方向的正应力影响很小，且角度为20°时，约束变化影响的区域仅限在主管焊缝上冠点与67.5°测点之间，同时也是应力集中的影响区域。

角度相同时，支管焊缝上SCF随约束变化情况如图9所示。

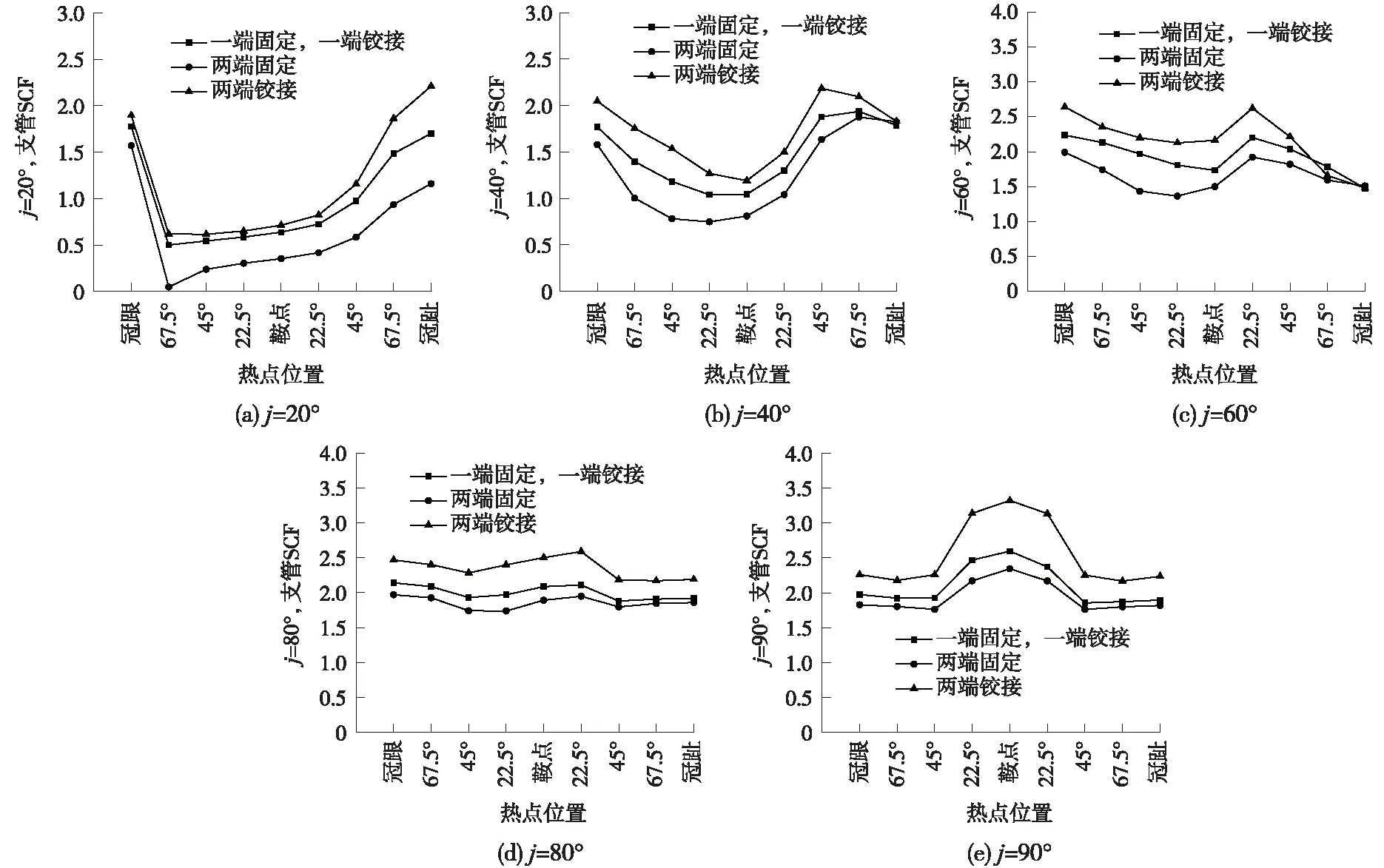
图9 支管SCF变化情况

约束不同时，各角度情况下，很明显看出，主管两端约束越强，支管热点应力集中系数越小，轴力沿支管轴线传递，不连续区域处，支管由轴向受力变为压弯组合受力，约束的加强，主管变形受到约束，膜应力减小，热点应力减小。各个角度一定时，约束变化仅改变支管热点应力分布的变化幅度，几乎不改变支管热点应力最大、最小值位置。

可见远端支撑条件变化时，即主管整体刚度发生变化时，对于热点应力的影响是有局限的，对于局部变形影响很小，对弯曲应力的贡献很小，而局部刚度的影响，如管径比、壁厚比等，则决定了最大、最小热点应力发生的位置即SCF分布特点。因此，Y型管节点具有一般性，其研究结论可为其他K型、N型等管节点参考。