神朔铁路钢轨折断风险评估模型研究

张晚秋,刘仍奎,李云芳,王福田

(1.北京交通大学轨道交通控制与安全国家重点实验室,北京 100044； 2.中国神华神朔铁路分公司,陕西榆林 719316)

引言

钢轨是轨道最重要的组成部分之一，直接承受列车荷载且引导车轮的运行方向，它的健康状态，直接关系到列车运行安全[1]。就神朔铁路而言，由于其具有运量大、轴重大、列车运行密度高等特点，导致轨道动态受力大，钢轨伤损出现概率较大，钢轨故障类型呈多元化发展，严重影响列车的运行安全[2]。因此有必要围绕神朔铁路钢轨折断风险事件进行风险评估，定量分析钢轨折断发生的可能性。

国内外有许多专家学者对钢轨折断风险事件开展过研究，Palese和Zarembski[3-4]利用统计方法分析了由钢轨折断造成的脱轨与钢轨伤损检出率之间的关系；Sourget和Riollet[5]构建了基于logistic回归方法的钢轨折断预测模型，用于预测特定位置发生钢轨折断的概率；Darwin[6]利用统计回归和人工神经网络两种技术开发了钢轨折断预测工具；Veskovic等[7]利用fuzzy logic模型对特定区段特定类型钢轨的断轨频率进行预测。冯宝锐、王元清等[8]分析了钢轨折断的关键致灾因素；杨凯、瞿福林等[9]利用故障树分析方法从钢轨折断机理角度研究了钢轨折断的主要原因；吴庆记[10]运用机理分析方法来研究钢轨折断原因。

本文参考国内外钢轨折断风险评估相关研究，在既有研究成果的基础上，基于模糊推理方法构建钢轨折断风险事件可能性计算模型，计算每日每200 m钢轨折断风险发生的可能性，辅助管理者实现钢轨折断风险精细化管理。

1 钢轨折断风险评估模型构建

1.1 致灾因子划分

依据国标《生产过程危险和有害因素分类与代码》[11]以及原铁道部文件《工务系统安全风险管理实施意见》[12]，结合神朔铁路实际情况，将钢轨折断风险事件致灾因子划分为人的因素、设备因素、环境因素和管理因素四大类，用Bj(j=1，2，3，4)表示；共10个致灾因子，用Ai(i=1，2，…，10)表示，详见表1。

表1 神朔铁路钢轨折断风险事件致灾因子划分

1.2 致灾因子状态量化评定模型

钢轨折断风险事件可能性评估的时间单位为“日”，用“d”表示；空间单位为“200 m钢轨单元区段”，设神朔铁路线路共划分成G个200 m单元区段(g=1，2，…，G，g表示单个区段的序号)，现以某一日某单元区段g为例来说明本文提出的致灾因子Ai的量化评定模型，令xi表示日期d区段g内致灾因子Ai的状态量化评定结果，xi计算模型如下

(1)人的因素B1类

A1：采用离日期d最近一次参与区段g钢轨探伤作业人员的业务考试成绩作为评定致灾因子A1的关键因素，令s表示业务考试成绩，本文提出A1的量化评定模型如下

(1)

A2：若区段g内存在焊缝，则采用离日期d最近一次参与区段g钢轨焊接作业人员的业务考试成绩，作为评定致灾因子A2的关键因素，A2量化评定模型与式(1)类似。若区段g内不存在焊缝，A2的量化评定结果为0。

(2)设备因素B2类

A3：采用钢轨伤损扣分数作为评定致灾因子A3的关键因素。依据神朔铁路钢轨伤损等级评分管理规定，本文确定“钢轨伤损等级为轻伤扣分1分，轻伤发展扣分2分，重伤扣分5分”的扣分原则，依据《修规》[13]设置钢轨伤损扣分阈值为10分，令n1表示日期d区段g中等级为轻伤的伤损数，n2表示日期d区段g中等级为轻伤发展的伤损数，n3表示日期d区段g中等级为重伤的伤损数，令n123=n1+n2+n3，本文提出A3的量化评定模型如下

(2)

A4：致灾因子A4的量化评定模型同A3。

A5：神朔铁路历史上发生的钢轨折断较大比例发生在小半径曲线上[14]，本文将半径≤1 000 m的曲线定义为小半径曲线区段，令R表示区段g曲线半径，提出A5的量化评定模型如下

(3)

A6：列车在坡度区段制动频繁，易导致钢轨伤损发展。设坡度阈值为神朔铁路最大坡度12‰，令h表示区段g坡度值，本文提出A6的状态量化评定模型如下

(4)

(3)环境因素B3类

A7：采用昼夜温差作为评定致灾因子A7的关键因素，利用距区段g最近的监测点离日期d最近的监测数据来确定日期d最高气温t1及最低气温t2，设阈值T为区段g历史最大温差值，提出A7的状态量化评定模型如下

(5)

A8：特殊地质地段是指风沙、风蚀地段和特殊岩土分布地段，根据神朔铁路实际情况对处于此地段的钢轨状态量化评定结果统一定为0.1，如下

(6)

A9：特殊路段是指桥梁、桥梁过渡段，隧道、隧道过渡段、道岔区段，列车通过特殊地段时冲击力较大，钢轨伤损发展较快，易导致钢轨折断。若区段g处于特殊路段则其量化评定模型如下

(7)

(4)管理因素B4类

A10：采用钢轨超期服役数作为评定致灾因子A10的关键因素，利用行车数据和调度指挥系统的确报数据来确定区段g的实际累计通过总重m，依据《修规》确定规定的钢轨大修通过总重M，提出A10量化评定模型如下

(8)

1.3 钢轨折断风险事件可能性评定模型

钢轨折断风险事件是一个复杂事件，致灾因子Ai的状态与钢轨折断风险事件发生可能性之间的关系难以建立精确的数学模型。模糊推理方法可以基于模糊推理规则模拟人的智能行为，有效拟合各类致灾因子与钢轨折断风险事件可能性之间的非线性关系[15]。本文所建立的钢轨折断风险事件可能性评定模型由6个模块组成，输入变量致灾因子状态值经过模糊化、模糊规则库建立、模糊推理、去模糊化等操作之后得到钢轨折断风险可能性，具体模型结构如图1所示。

图1 钢轨折断风险事件可能性评定模型结构

1.3.1 模糊化

模糊化方法又称模糊集合论方法，指把待考察的对象及反映它们的模糊概念看成一种模糊集合，建立适当的隶属度函数，通过对模糊集合的有关运算和变换，对所考察对象进行定量分析。

(1)输入输出变量确定

由于神朔铁路钢轨折断风险事件的致灾因子较多，若直接用致灾因子的模糊值推理钢轨折断风险事件发生可能性的模糊值，则会产生较多模糊规则，不便于现场实际操作。本文钢轨折断风险评估模型将基于致灾因子大类Bj建立，即将B1、B2、B3、B4这四大类致灾因子的状态作为模型输入变量，输出变量为钢轨折断风险发生的可能性。

令yj(j=1，2，3，4)表示Bj的状态评定结果，即yj是由属于Bj的致灾因子Ai的状态xi所决定的，即存在一种映射关系yj=f(xi)，一般可通过统计建模来寻找yj与xi之间的规律，采用平均数方法来计算yj

(9)

(2)输入输出变量模糊集合划分

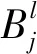
(3)隶属度函数选取

隶属度函数有多种不同形式，但在解决和处理模糊信息问题上具有殊途同归的效果[17]。选取常用的高斯型隶属度函数进行致灾因子模糊化，详见式(10)。

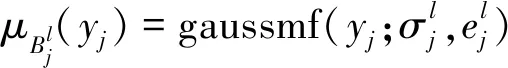
(10)

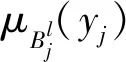
本文输出变量钢轨折断风险可能性选取三角形隶属度函数，函数形式

μCl(z)=trimf(z;al，bl，cl)

(11)

式中，z表示输出模糊向量；μCl(z)表示z对模糊集合Cl的隶属度；trimf表示三角形隶属度函数；al、bl、cl为钢轨折断风险可能性隶属度函数参数，确定方法同上，其中(a低，b低，c低)=(0，e-6，e-5)。

1.3.2 模糊规则库建立

模糊规则库是模糊推理过程的核心部分，由若干模糊推理规则组成，是将致灾因子量化结果的模糊向量对应到钢轨折断风险发生可能性模糊向量的过程[17]。

模糊推理规则形式为

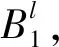
(12)

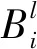
作者通过调研神朔铁路管理现状，建立了钢轨折断风险事件模糊推理规则，此规则可随着模型应用时间不断调整完善。本模型所建立的钢轨折断风险事件发生可能性规则如图2所示。

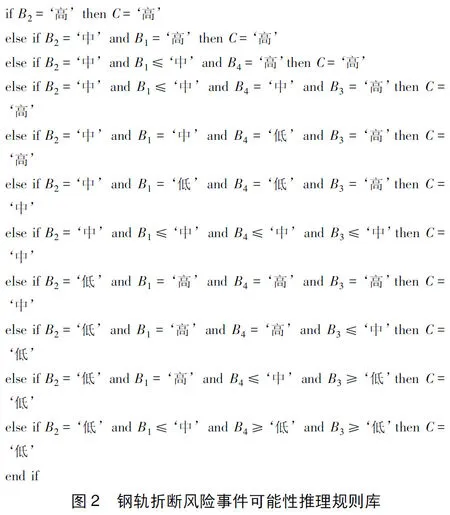
1.3.3 模糊推理与去模糊化

模糊推理是在模糊逻辑原则的基础上，利用模糊规则决定如何将输入论域U上的模糊集合与输出论域V上的模糊集合对应起来。采用应用广泛的Mamdani算法，推理钢轨折断风险事件发生可能性的模糊值，Mamdani型模糊推理可以通过事先确定的一组推理规则实现从输入到输出的推理计算，从而建立准确的模糊推理机制[17]。

令z*表示钢轨折断风险事件发生可能性精确值，采用重心解模糊器(式(13))去模糊化。

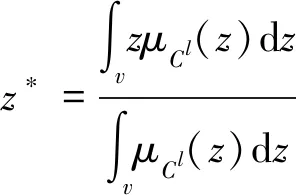
(13)

1.4 钢轨折断风险事件可能性等级评定

本文依据ALARP[18]准则，参照国标GB/T 27921—2011《风险管理风险评估技术》[19]，将神朔铁路钢轨折断风险事件可能性划分为5个等级，Ⅰ(经常)、Ⅱ(可能)、Ⅲ(偶尔)、Ⅳ(很少)和Ⅴ(几乎不可能)，并将可能性等级从高到低分别用红色、橙色、黄色、蓝色和绿色表示。依据《轨道交通安全风险管理》[20]确定风险可能性划分阈值，详见表2。将式(13)计算出的z*与表2对照可以确定区段g在日期d的钢轨折断风险可能性等级情况。

表2 钢轨折断风险可能性等级判定规则

2 模型验证

2.1 数据准备

选取神朔铁路神木北至黄羊城区间上行K30+000～K40+000共50个 200 m钢轨单元区段g为研究对象，收集其2014年3月23日～2015年3月23日的钢轨病害数据和钢轨折断致灾因子数据，基于1.3节建立的钢轨折断风险评估模型，计算2015年3月24日50个200 m单元区段钢轨折断风险事件发生的可能性。

2.2 模型计算过程

2.2.1 致灾因子量化评定结果

基于式(1)～式(9)，结合区间K30+000～K40+000的致灾因子数据，可得到所选区段2015年3月24钢轨折断风险事件致灾因子状态评定结果xi以及各大类致灾因子状态评定结果yj，具体如表3和表4所示。

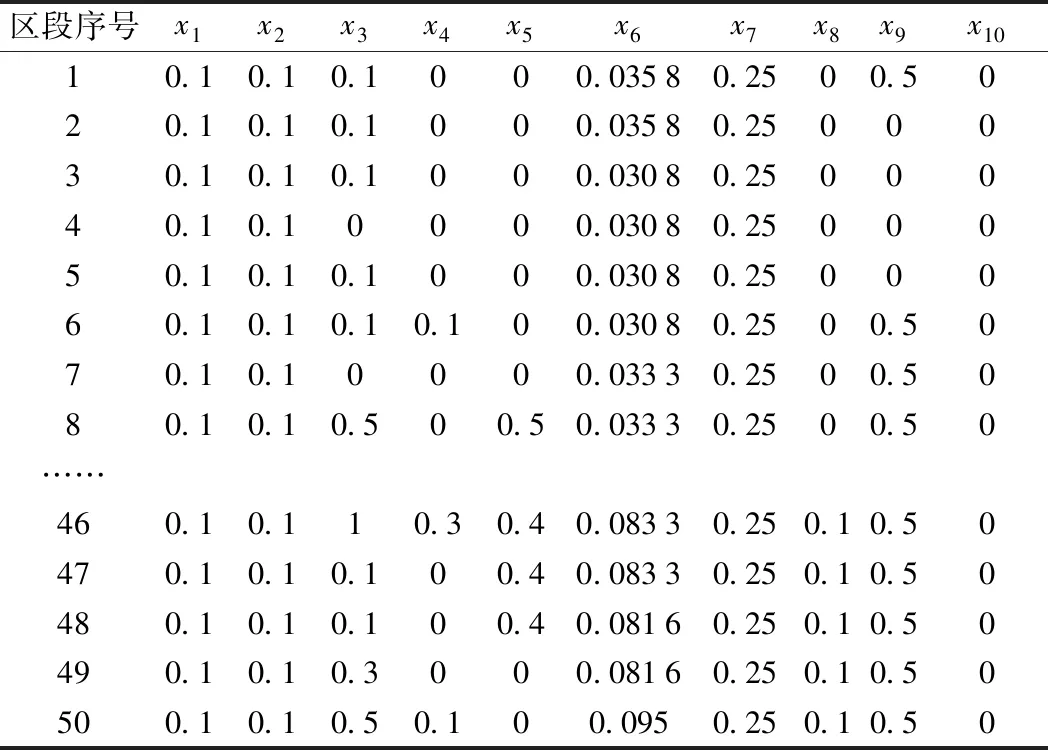
表3 区段g致灾因子状态评定结果xi(部分)

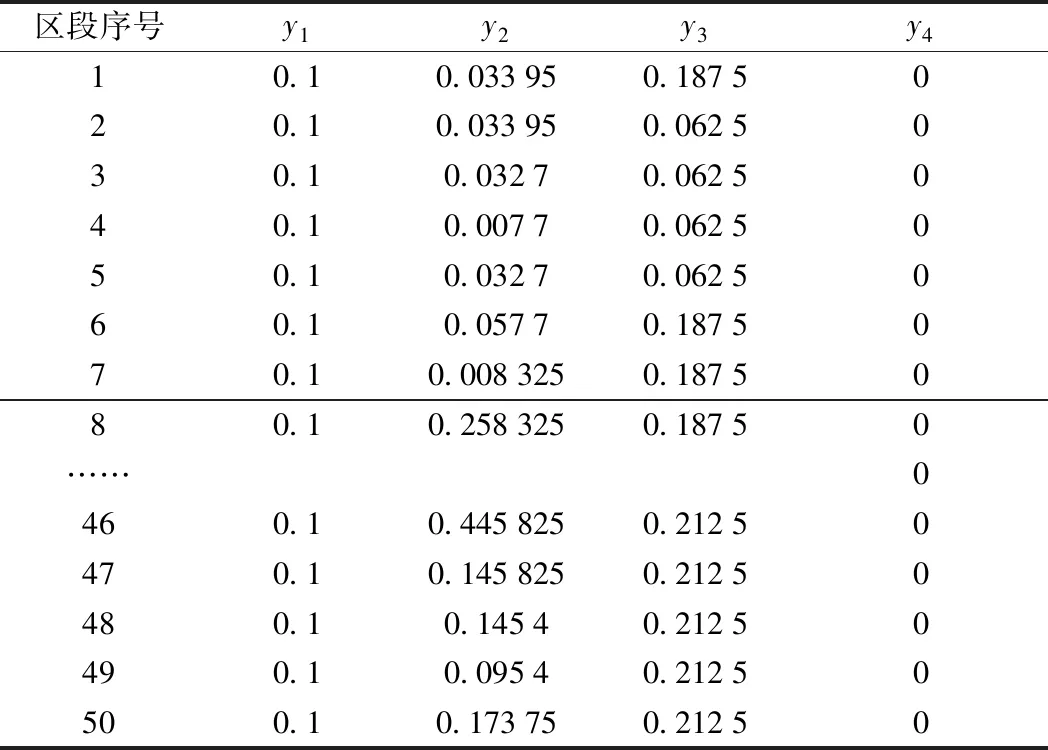
表4 区段g致灾因子大类状态评定结果yj(部分)

2.2.2 钢轨折断风险事件可能性计算

基于钢轨折断致灾因子状态量化结果及建立的钢轨折断风险事件可能性评定模型，利用Matlab软件进行计算，可得到神朔铁路K30+000～K40+000上行共50个200 m区段在 2015年3月24日的钢轨折断风险可能性，得出这50个区段g在2015年 3月24日钢轨折断风险事件可能性随空间位置变化的趋势，如图2所示。

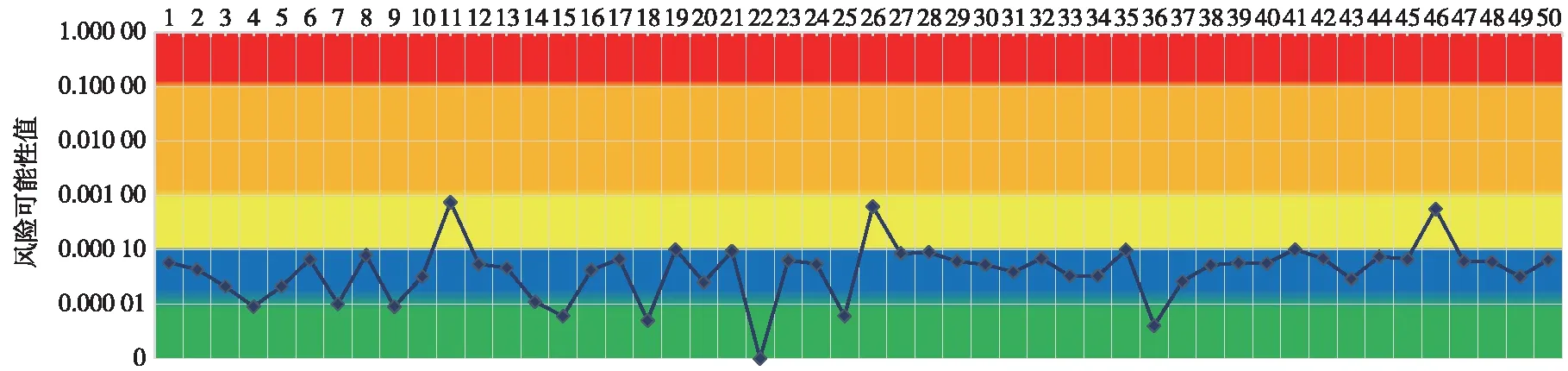
图2 2015年3 月24日神朔铁路K30+000～K40+000区间钢轨折断风险可能性变化趋势

2.3 模型结果分析

根据2.2节的计算结果，神朔铁路区间K30+000～K40+000内共有3个单元区段属于钢轨折断高风险单元，47个低风险单元。详见表5。

表5 钢轨折断风险可能性等级判定结果

为了验证模型的有效性，收集了该50个单元区段2015年3月24日～4月24日的实际钢轨病害数据，表6为其中7个单元区段的预测结果与实际数据的对比，包括3个Ⅲ级高风险单元区段、2个Ⅳ级风险单元区段及2个Ⅴ级风险单元区段。这7个单元区段的实际钢轨病害情况与模型计算出的风险程度较为一致，这说明了模型的有效性，对钢轨折断风险管理具有指导意义。

表6 模型计算数据与实际钢轨病害数据对比

3 结论

(1)以200 m为单元区段，建立基于模糊推理方法的钢轨折断风险可能性评估模型，计算钢轨折断风险发生可能性大小，有效评估风险可能性的等级，精确确定钢轨折断高风险发生的位置，有助于实现钢轨折断风险事件的精细化管理。

(2)钢轨折断风险具有动态性，区段内钢轨折断风险发生可能性随着致灾因子状态不断变化，不同时间空间位置上的致灾因子状态不同，构建的钢轨折断风险评估模型可以计算出每日每200 m区段内钢轨折断风险事件发生的可能性，实现钢轨折断风险的动态管理。

本文计算过程需要处理大量致灾因子数据和钢轨伤损数据，为实现神朔铁路钢轨折断风险智能化和信息化管理，接下来，笔者将主要研究如何利用信息技术将本文的钢轨折断风险评估方法转化为现场可利用的工具。