快堆系统分析程序FASYS堆芯分析模块验证
2020-02-25张东辉
王 晋,张东辉
(中国原子能科学研究院,北京 102413)
快堆系统分析程序可分析快堆电厂在各种瞬态过程中系统的响应[1],进行快堆研究的国家和机构开展了大量的快堆系统分析程序开发和验证。目前快堆系统分析程序主要有两大类:一类是由水堆系统分析程序经过模型升级和修改成为可适用于快堆分析的系统分析程序,如RELAP5-3D©[2]、TRACE[3]、CATHARE[4]、ATHLET[5]等;另一类是专门为快堆系统分析而研发的系统分析程序,如SSC-L[6]、SSC-P[7]、SAS4A/SASSYS-1[8]、SAM[9]、DINROS[10]、OASIS[11]、SSC-K[12]、MARS-LMR[13]等。
FASYS程序是中国原子能科学研究院自主开发的快堆系统分析程序,包含堆芯分析模块、一二回路模块、事故余热排出系统模块等,已对FASYS程序的中子物理模型、水力模型、热工模型和整体模型进行了初步验证[14-15]。目前FASYS程序正用于中国示范快堆反应性的意外变化类事故的分析,主要关注堆芯关键现象的分析计算。
DINROS程序(俄罗斯快堆系统分析程序)曾用于БН-600和БН-800快中子反应堆的安全分析报告的编写及БН-350反应堆安全保护手段的研制,该程序已在БН-350、БН-600、БP-10等装置或反应堆上经过验证计算。中国实验快堆曾引进DINROS程序进行安全分析报告的编制。SAS4A/SASSYS-1程序(以下简称SAS程序)由美国阿贡国家实验室开发,其中包括SAS4A程序和SASSYS-1程序。SAS4A程序是严重事故程序,SASSYS-1程序是快堆系统分析程序,可用于分析与系统相关的典型事故的序列,也是EBR-Ⅱ仿真机的计算引擎,被广泛地用于快堆事故的分析中[8]。
FASYS程序堆芯分析模块包括点堆、衰变热、反应性反馈、堆芯通道热工水力模型等,本文通过点堆方程解析解算例、DINROS程序超功率算例、SAS4A/SASSYS-1程序点堆与衰变热算例、反应性反馈算例、燃料棒与冷却剂换热算例,进行FASYS程序堆芯分析模块的所有关键模型的验证,并对堆芯分析模块的计算偏差进行初步评估。
1 FASYS程序堆芯分析模块介绍
FASYS程序堆芯分析模块包括点堆、衰变热、反应性反馈、堆芯通道热工水力模型等。FASYS程序采用3阶Hermite插值多项式法[16]求解点堆动态方程。在计算反应堆功率时,除考虑裂变功率外,还考虑裂变产物和锕系元素的衰变功率,并考虑了反应堆连续运行史对上述衰变功率的影响。FASYS程序堆芯通道热工水力模型采用单通道模型,堆芯可划分为任意数目的通道来模拟燃料组件、屏蔽组件、不锈钢组件等。文献[14]给出了FASYS程序点堆、衰变热、堆芯通道热工水力模型的具体方程。FASYS程序可计算的反应性分项包括输入卡定义的引入反应性、控制棒引入的反应性、燃料多普勒反应性反馈、燃料和包壳轴向膨胀反应性反馈、冷却剂密度变化反应性反馈、堆芯径向膨胀反应性反馈。其中,燃料多普勒反应性反馈、燃料和包壳轴向膨胀反应性反馈、冷却剂密度变化反应性反馈提供集总参数模型和空间分布模型两个选项。
2 验证结果
2.1 点堆方程解析解算例
本算例将采用点堆方程解析解对FASYS程序的点堆模型进行验证,解析解的来源为公开发表的文献[16],包括3种不同情况下解析解与FASYS程序数值解的比较。
情况1:
M=1,β=0.006 5,
λ=0.08 s-1,Λ=1.0×10-8s

式中:M为缓发中子组数;β为缓发中子有效份额;λ为先驱核衰变常量;Λ为瞬发中子寿命;ρ为引入的外部反应性。
情况2:
M=15,β=0.007 330 19,
Λ=2.15×10-4s(动态参数见文献[16])

情况3:
M=1,β=0.006 5,
λ=0.08 s-1,Λ=1.0×10-8s
ρ(t)=0.003sin(πt/10)
情况1和情况2均为0 s时刻引入0.002阶跃反应性,但中子动态参数不同,情况1仅有1组缓发中子,情况2有15组缓发中子。表1列出情况1解析解与FASYS程序计算值(N(t)/N(0))的对比,共计算时间步长分别为0.1、0.01、0.001、0.000 1和0.000 01 s等5种情况,由于0 s时刻引入的阶跃反应性较大,采用的时间步长不能满足程序设定的精度要求,程序中自动减小了时间步长,以上5种情况在0 s时刻的实际计算时间步长均为10-6s量级,0 s时刻之后采用原设置的时间步长。从表1可知,当时间步长为0.1 s时,相对偏差为10-3量级,当时间步长减小1个量级,计算精度约提高1个量级。表2列出情况2解析解与FASYS程序计算值的对比,可看出当时间步长为0.001 s时,相对偏差为10-5量级,时间步长越小,计算精度越高。情况3引入随时间变化的正弦反应性,中子动态参数与情况1相同。表3列出情况3解析解与FASYS程序计算值的对比,可看出当时间步长为0.01 s时,FASYS程序计算值即可与解析解保持6位有效数字的一致。
通过情况1、2、3的计算对比可发现,FASYS程序采用的3阶Hermite插值法计算的数值结果在一般情况下较为精确,对于引入较大阶跃反应性的情况需采取较小的时间步长才能保证计算精度,在实际计算中应评估引入的反应性并进行时间步长影响分析,选取合适的时间步长以保证计算精度。

表1 不同时间步长下情况1解析解与FASYS程序计算值的对比Table 1 Comparison between analytical solution and FASYS code calculated value of case 1 at different time steps

表2 不同时间步长下情况2解析解与FASYS程序计算值的对比Table 2 Comparison between analytical solution and FASYS code calculated value of case 2 at different time steps
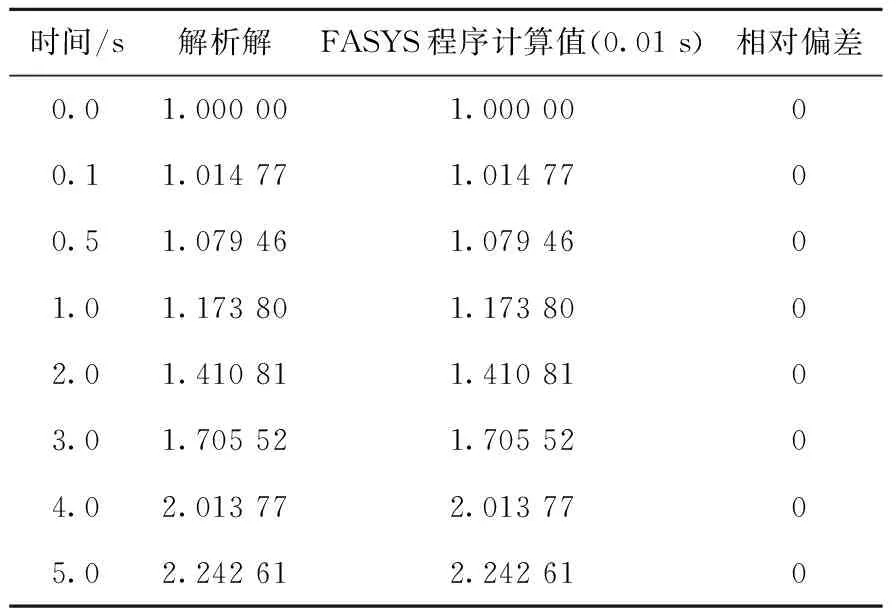
表3 情况3解析解与FASYS程序计算值的对比Table 3 Comparison between analytical solution and FASYS code calculated value of case 3
2.2 DINROS程序超功率算例
本算例将采用中国实验快堆[10]“在堆各种状态下补偿棒非规定位移”预计运行事件分析中对0.1%额定功率运行工况的计算结果进行对比验证,原分析结果由DINROS程序计算。工况假设如下:1) 相对流量取0.25;2) 堆芯冷却剂入口温度为250 ℃;3) 堆内无反馈;4) 棒价值取平衡态初期的值,引入反应性7.77×10-4Δk/k,在5 s内线性引入。
表4列出了FASYS程序计算的主要事故序列与原事故序列的对比,可看出,FASYS程序计算的达到堆相对功率保护参数和最大值的时间与DINROS程序计算值一致,堆相对功率最大值的相对偏差为8.9×10-4。

表4 主要事故序列对比Table 4 Comparison of main accident sequences

图1 反应堆相对功率的结果对比Fig.1 Comparison of normalized power results
图1、2分别为反应堆相对功率和反应堆周期的FASYS程序计算值与DINROS程序计算值的对比,从结果可看出,FASYS程序计算值与DINROS程序计算值符合很好。
2.3 SAS程序点堆与衰变热计算算例
本算例将采用SAS程序作为校验程序对FASYS程序的点堆模型和衰变热模型进行验证,计算建模基于中国实验快堆,假设反应堆已满功率连续运行80 d,0~6 s向反应堆线性引入负反应性,反应性速率为-728.68 pcm/s,6 s时负反应性引入结束,共引入负反应性-4 372.08 pcm。不考虑反应性反馈,计算停堆过程中的裂变功率和衰变功率。

图2 反应堆周期的结果对比Fig.2 Comparison of nuclear reactor period results
表5列出了衰变功率相对值、总功率相对值,可看出,衰变功率的最大相对偏差出现在0 s时刻,为7.4×10-7。总功率的最大相对偏差出现在前期,主要来源于两个程序求解点堆方程的方法不同,后期由于衰变功率占总功率的绝大部分,总功率的相对偏差也逐步减小。总体而言,本算例中FASYS程序与SAS程序的衰变功率最大相对偏差为10-7量级,而总功率最大相对偏差为10-6量级。

表5 衰变功率相对值、总功率相对值Table 5 Normalized decay power results and normalized total power results
2.4 SAS程序反应性反馈算例
本算例将采用SAS程序作为校验程序对FASYS程序的反应性反馈模型进行验证,将验证具有空间分布模型的燃料多普勒反应性反馈、燃料和包壳轴向膨胀反应性反馈、冷却剂密度变化反应性反馈。本算例中FASYS程序与SAS程序采用空间分布相同的钠空泡反应性系数、多普勒常数、燃料质量增加引入的反应性、包壳质量增加引入的反应性。
情况1堆芯零功率,其初始温度均为358 ℃,0~50 s时间内堆芯入口温度线性上升至458 ℃,50~100 s堆芯入口温度一直保持在458 ℃;情况2堆芯零功率,堆芯初始温度均为358 ℃,0~50 s时间内堆芯入口温度线性下降至258 ℃,50~100 s堆芯入口温度一直保持在258 ℃。
表6列出了情况1在100 s时反应性反馈值的FASYS程序计算值与SAS程序计算值的对比。其中,钠密度变化引入的反应性反馈计算值相对偏差绝对值为1.3×10-3,轴向膨胀引入的反应性反馈计算值相对偏差绝对值为6.6×10-4,多普勒效应引入的反应性反馈计算值相对偏差绝对值为1.1×10-3。表7列出了算例2在100 s时反应性反馈值的FASYS程序计算值与SAS程序计算值的对比。其中,钠密度变化引入的反应性反馈计算值相对偏差绝对值为1.3×10-3,轴向膨胀引入的反应性反馈计算值相对偏差绝对值为1.1×10-3,多普勒效应引入的反应性反馈计算值相对偏差绝对值为1.1×10-3。总体来说,FASYS程序计算的反应性反馈与SAS程序相比,其相对偏差为10-3量级。

表6 情况1反应性反馈计算值对比Table 6 Comparison of reactivity feedback results for case 1

表7 情况2反应性反馈计算值对比Table 7 Comparison of reactivity feedback results for case 2
2.5 SAS程序燃料棒与冷却剂换热计算算例
本算例将采用SAS程序作为校验程序对FASYS程序的堆芯通道热工水力模型进行验证,采用相同的燃料组件几何参数、节点划分、功率、流量、轴向功率分布、包壳物性、燃料物性。其中,燃料棒轴向共划分24个节点,芯块径向等距划分为5个节点,包壳径向划分为3个节点,冷却剂径向为1个节点。对100%功率稳态情况下和100%功率线性升功率到110%功率瞬态情况下SAS程序与FASYS程序计算的燃料温度、包壳温度、冷却剂温度进行结果对比。
图3为100%功率稳态情况下SAS程序与FASYS程序计算的燃料最高温度、包壳中壁温度、冷却剂温度的轴向分布结果对比。其中,燃料最高温度、包壳中壁温度、冷却剂温度的最大偏差绝对值均为0.2 ℃。
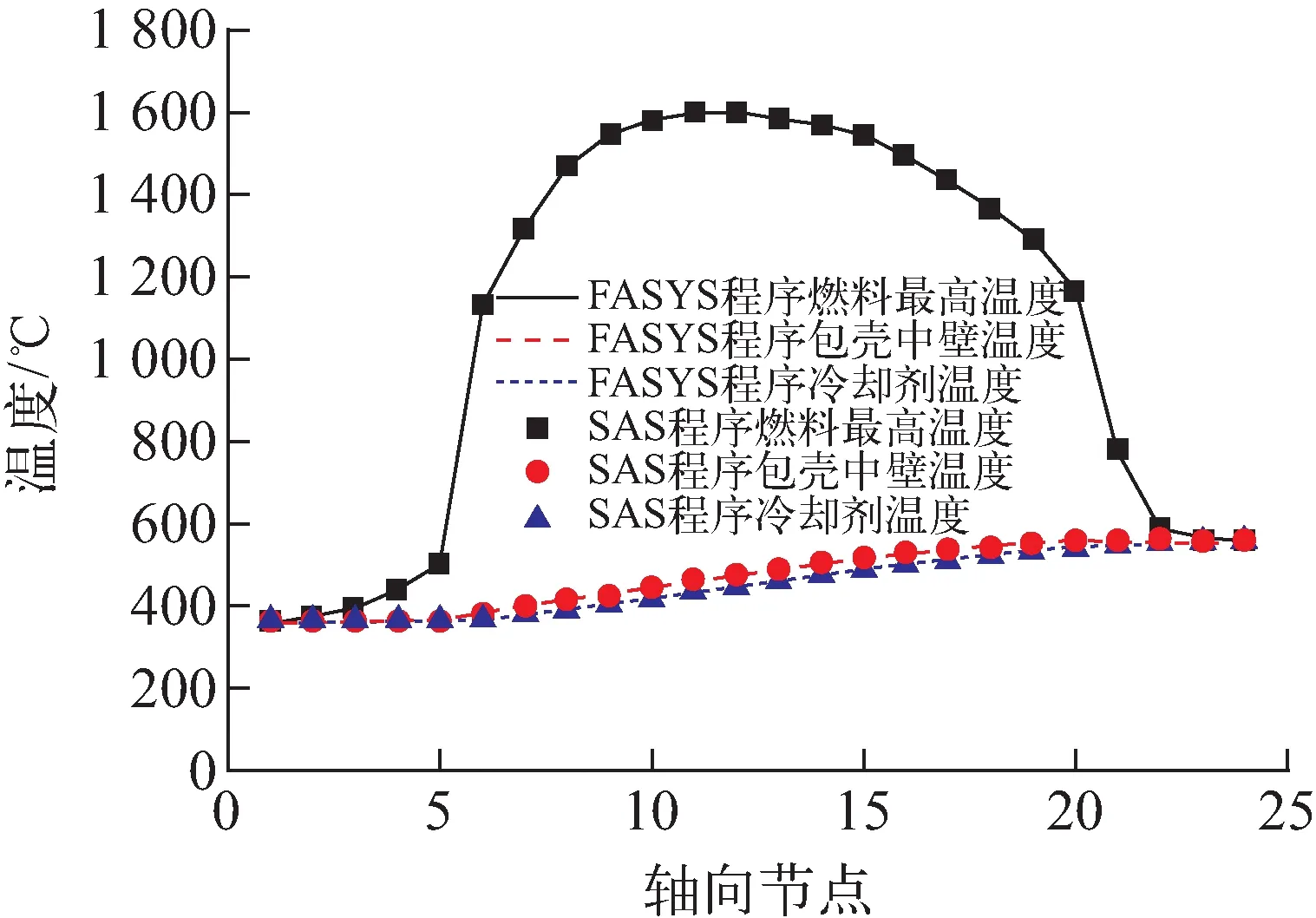
图3 组件轴向温度的稳态结果对比Fig.3 Comparison of subassembly axial temperature steady state results
瞬态计算中,0 s时刻燃料组件为100%功率然后线性升功率,8 s时刻达到110%功率后保持不变,期间流量保持不变,时间步长为0.001 s。图4为FASYS程序与SAS程序的瞬态燃料最高温度结果对比,瞬态情况下最大偏差绝对值为0.1 ℃。图5为FASYS程序与SAS程序的瞬态包壳中壁最高温度与冷却剂最高温度结果对比,瞬态情况下包壳中壁最高温度最大偏差绝对值为0.4 ℃,冷却剂最高温度最大偏差绝对值为0.7 ℃。

图4 瞬态燃料最高温度的结果对比Fig.4 Comparison of fuel maximum temperature transient results
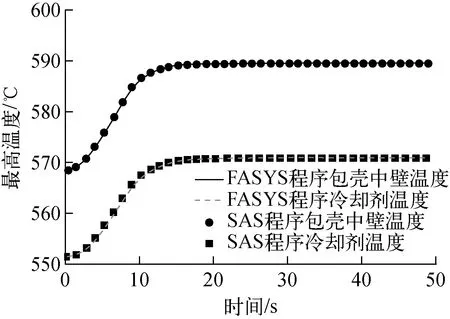
图5 瞬态包壳中壁最高温度和冷却剂最高温度的结果对比Fig.5 Comparison of cladding middle wall maximum temperature and coolant maximum temperature transient results
分析时间步长对图4、5瞬态温度计算的影响,分别计算时间步长为0.01、0.001和0.000 1 s等3种情况,如表8所列,时间步长0.01 s的计算结果与时间步长0.000 1 s相比温度最大偏差为0.07 ℃,时间步长0.001 s的计算结果与时间步长0.000 1 s相比温度最大偏差为0.01 ℃。

表8 不同时间步长下瞬态温度偏差对比Table 8 Comparison of transient temperature deviations at different time steps
注:温度偏差指与时间步长为0.000 1 s的计算结果的偏差
分析网格划分对燃料棒温度计算的影响,由于轴向节点划分方式来自物理专业给出的轴向功率分布,此处仅分析芯块径向节点划分数目对计算的影响。分别计算芯块径向节点数目为5、6、9、11、13、15、17、21、31、41等10种情况,对比前9种情况的燃料最高温度计算值与第10种情况计算值的偏差,如图6所示,可看出随着径向节点数目的增加,燃料最高温度计算值减小,偏差亦减小,当径向节点大于21时,燃料温度计算偏差小于0.1 ℃,基本实现径向网格无关性。
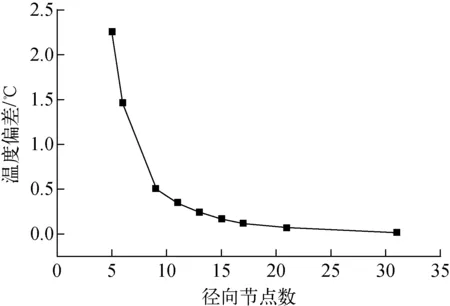
图6 不同径向节点数的燃料温度偏差对比Fig.6 Deviation comparison of fuel temperature results with different numbers of radial nodes
分析功率和流量的偏差对图4和图5瞬态温度计算的影响,分别计算瞬态最大功率增加1%、增加0.1%、瞬态流量减小1%、减小0.1%等情况,如表9所列,功率增加1%和流量减小1%引起的包壳温度、冷却剂温度偏差相当,而功率增加1%引起的燃料温度偏差为13.5 ℃,远大于流量减小1%引起的燃料温度偏差1.0 ℃。

表9 功率、流量偏差对瞬态温度的影响Table 9 Effect of power and flow deviations on transient temperature
注:温度偏差指与SAS程序原瞬态计算结果的偏差
3 堆芯分析模块的计算偏差评估
以FASYS程序进行中国实验快堆的调节棒非规定位移事故分析为例,对堆芯分析模块的整体计算偏差进行分析。首先给出调节棒非规定位移事故分析的事故描述和事故假设,反应堆处于正常运行期间,1根调节棒从底部失控提升到顶,1根调节棒价值为0.001 748 Δk/k,假设反应性线性引入,反应性引入速率为11.66 pcm/s,反应性引入时间从0 s开始到15 s结束。事故假设初始状态100%额定功率上叠加2.5%,堆芯冷却剂入口温度在额定值360 ℃上叠加3 ℃,紧急停堆共引入负反应性-0.016 8 Δk/k,停堆反应性在1.4 s内引入完成。表10列出计算时间步长取0.001 s时的主要事故序列。
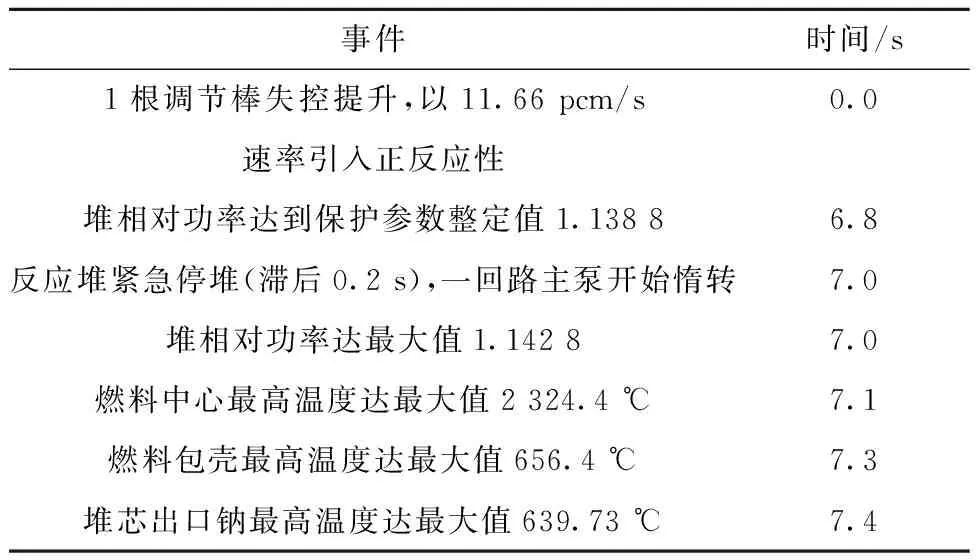
表10 主要事故序列Table 10 Major accident sequences
分析计算时间步长h对结果的影响,图7a为时间步长取0.01、0.001 s的功率计算结果与时间步长0.000 1 s的功率计算结果的相对偏差,可看出在7.0 s时,由于紧急停堆短时间内(1.4 s)引入较大的负反应性,计算偏差急剧上升,时间步长取0.01 s的计算偏差从1×10-4瞬间上升到4×10-2,时间步长取0.001 s的计算偏差从1×10-5瞬间上升到1×10-3,紧急停堆结束后,由于不再引入较大的负反应性,时间步长取0.01 s的计算偏差降低到约1×10-3,时间步长取0.001 s的计算偏差降低到约1×10-4。图7b为时间步长取0.01、0.001 s的燃料最高温度计算结果与时间步长0.000 1 s的燃料最高温度计算结果的偏差,时间步长取0.01 s的燃料最高温度计算值偏差约10 ℃,时间步长取0.001 s的燃料最高温度计算值偏差约0.2 ℃,由表8、9和图6可知,不同时间步长的燃料最高温度计算值偏差主要来自功率的计算偏差。图7c为时间步长取0.01、0.001 s的包壳、冷却剂最高温度计算结果与时间步长0.000 1 s的包壳、冷却剂最高温度计算结果的偏差,时间步长取0.01 s的包壳最高温度计算值偏差约1 ℃、冷却剂最高温度计算值偏差约0.4 ℃,时间步长取0.001 s的包壳最高温度计算值偏差约0.1 ℃、冷却剂最高温度计算值偏差约0.1 ℃,不同时间步长的包壳、冷却剂最高温度计算值偏差应来自燃料温度的计算偏差。
综合第2章对堆芯分析模块各模型的验证结果及本章结果可知,在引入较大反应性的情况下时间步长对点堆方程的求解精度有较大影响,对温度计算偏差的影响最大,径向节点的划分数目对燃料温度计算的影响次之,随着径向节点数目的增加,燃料最高温度计算值减小。在此类事故的分析中,应首先评估引入的外部反应性,然后进行时间独立性分析,选取合适的时间步长,进行网格无关性分析,得到满足计算偏差要求的径向节点数目。

图7 不同时间步长下功率、燃料最高温度以及包壳、冷却剂最高温度偏差对比Fig.7 Comparison of deviations for power, fuel maximum temperature, and cladding and coolant temperatures at different time steps
4 结论
通过点堆方程解析解算例、DINROS程序超功率算例、SAS4A/SASSYS-1程序点堆与衰变热算例、反应性反馈算例、燃料棒与冷却剂换热算例,对FASYS程序的堆芯分析模块的所有关键模型进行验证,结果均符合良好。对堆芯分析模块各关键模型和整体计算偏差进行了初步评估,在引入较大反应性的情况下点堆方程的求解精度依赖于时间步长,功率计算值的偏差直接影响温度计算的准确性,径向节点的划分数目对燃料温度计算的影响次之,随着径向节点数目的增加,燃料最高温度计算值减小,为进行中国示范快堆反应性的意外变化类事故分析和计算偏差估计提供参考。
