自然循环棒束形通道流动不稳定性起始点研究
2020-02-25李宗洋高璞珍林宇琦阿不都赛米亚库甫
李宗洋,高璞珍,王 强,林宇琦,阿不都赛米·亚库甫
(哈尔滨工程大学 核安全与仿真技术国防重点学科实验室,黑龙江 哈尔滨 150001)
自然循环能提高核反应堆系统的固有安全性,许多新型反应堆内都有采用自然循环系统,如HPR1000、APR+[1]。核电站运行时,核反应堆内的所有部件中,只有主循环泵是运动的。主循环泵运转过程中会发出噪声,同时也消耗大量的能源。而自然循环系统依靠冷热段的密度差为流体提供驱动力,从而可达到取消泵简化系统的目的。

图1 实验装置示意图Fig.1 Schematic of experimental apparatus
核反应堆堆芯内存在棒束形通道,在核反应堆运行中,棒束形通道内有可能会因受到热力学因素诱导而产生流动不稳定性振荡:莱迪内格流动不稳定性、密度波不稳定性(DWO)、热力学不稳定性(THO)和压力降不稳定性(PDO)[2-3]。这些不稳定性会造成装置的机械振动、热力学疲劳,使系统难以操控甚至损坏装置[4-5]。例如,对于超临界水反应堆,流动不稳定性造成的水物性参数改变,尤其是水的密度,会威胁到反应堆运行安全[6-7]。因此,核反应堆系统要求尽量避免或预判这些不稳定性,以及在设计过程中尽可能地提供一个安全余量从而确保装置的安全性和可靠性。为能预判流动不稳定性,许多学者针对不稳定性起始点(OFI)进行了大量研究,并得出了一些关于计算OFI对应的热流密度的经验关系式。一些学者针对环形[8-9]、管形[10]、多孔介质[11]和矩形通道[12-13],得出了相应的热流密度的经验关系式。但对于棒束形通道的研究还很少。
在两相流动不稳定性研究中,除实验外,还常用到RELAP5程序进行数值模拟研究,该程序用于计算分析轻水反应堆[14]。该程序最初的设计目的是对核反应堆系统中高压强迫循环工况进行数值模拟。通过将程序与大量实验数据对比,对其不断完善,使得其在高压强迫循环工况下的适用性得到了很好的验证。因为基于该程序研究的低压自然循环工况较少,使得其关于低压自然循环工况的数值模拟准确性和适用性以及可靠性仍需进一步验证。
本文在低压自然循环条件下,针对棒束形通道进行两相OFI实验和RELAP5数值模拟研究,以得到工程设计上具有参考价值的结果。通过驱动力的方法分析OFI产生的机理,并验证RELAP5对低压自然循环棒束形通道OFI研究的适用性。
1 实验
1.1 实验装置
自然循环棒束形通道实验台主要由预热器、棒束实验段、冷凝器、稳压器、阀门和测量仪表等组成,如图1所示。实验工质为蒸馏水。蒸馏水在预热器内被加热到一定的温度,然后进入到棒束实验段中再次被加热,接着在冷凝器中被二次侧来自于冷却水池的冷却水冷却,最后回到预热器。整个系统的压力通过给稳压器充入氮气或打开泄压阀排气实现控制。整个实验系统中,通过温度、压力和流量测量仪器仪表,将这些信息收集到信息采集系统中。
稳压器高度为1 200 mm,直径为200 mm,可提供很大的可压缩气空间。通过改变阀门1和阀门2闭合状态可控制稳压器的连接位置,即棒束实验段上游(阀门1开启和阀门2关闭)或下游(阀门1关闭和阀门2开启)。预热器长度为1 400 mm,直径为200 mm。冷凝器长度为1 310 mm,换热面积约为3.0 m2。
棒束形通道详细信息如图2所示,用直流电源加热9根不锈钢棒束(3×3)。不锈钢棒束形通道长度为900 mm,有效加热长度为800 mm。整个棒束形通道的上、下端分别由定位格架1和2固定。棒直径用D表示,两根棒圆心之间的距离为1.33D,棒束外面是边长为4.33D的正方形盒。正方形盒和棒束形通道中间流过的是冷却剂。整个正方形盒放在一个更大的圆柱形压力容器中,该压力容器可承受15.5 MPa的压力(图1)。

图2 棒束形通道示意图Fig.2 Schematic of rod bundle channel
1.2 实验数据不确定度分析
实验数据分为直接测量量和间接测量量。直接测量量是通过相应的仪器仪表直接测量获得的,而间接测量量是通过不确定度传递公式计算获得的。本实验中,压力、温度和流量等热工水力参数可通过传感器和相应的测量仪表直接获得,因此其不确定度与相应的仪器仪表的测量精度密切相关。棒束形通道的尺寸用游标卡尺测量获得,其测量精度为0.02 mm。而其他位置管道等的尺寸则用卷尺测量获得,其测量精度为1 mm。其他直接测量仪表的精度列于表1。间接测量的热工水力参数主要有棒束形通道加热段的当量直径、功率、热流密度和质量流量等,计算结果列于表2。
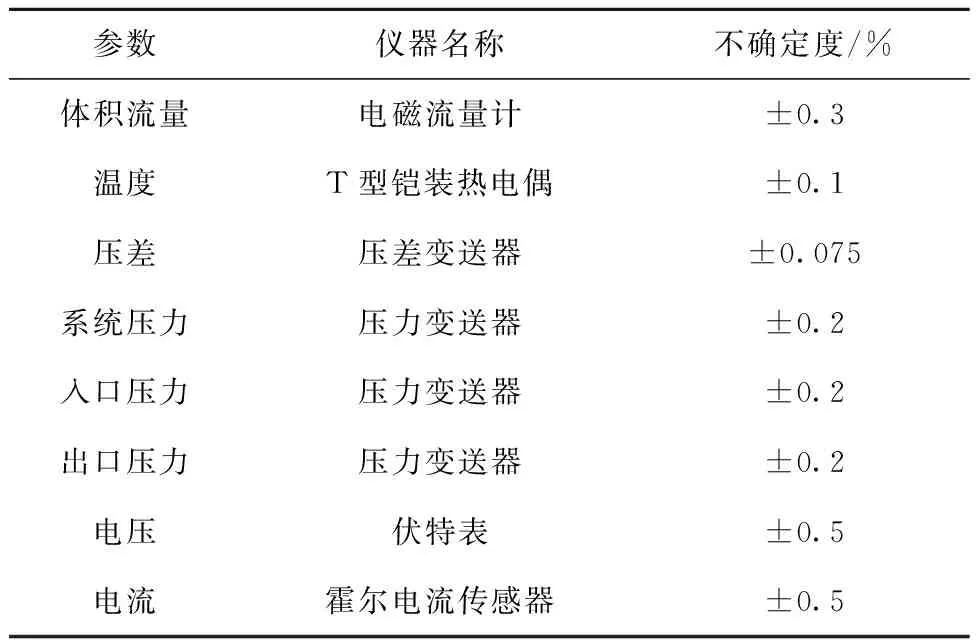
表1 直接测量量的不确定度Table 1 Uncertainty of direct measurement parameter

表2 间接测量量的不确定度Table 2 Uncertainty of undirect measurement parameter
1.3 实验流程
实验主要分为两部分,即自然循环单相稳态和两相流动不稳定态。由于本实验为一个自然循环闭合回路,实验中的稳压器内气空间的体积膨胀和压缩都会影响到稳压器的水位和系统压力,因此本实验中的系统压力是指自然循环单相稳态时的初始压力。实验相关参数的取值范围列于表3。考虑到测量仪表的测量误差,本研究中只有当某一热工参数数值出现波动幅值大于或等于主值的10%才会被认为出现了流动不稳定性,此时对应的热流密度则为OFI对应的热流密度。
1) 单相稳态
先关闭阀门5并开启阀门6和泵,通过泵建立强迫循环。用低热流密度(29.47 kW/m2)对棒束形通道进行加热,通过预热器将蒸馏水加热至预期的入口过冷度。当冷凝器出口温度和棒束实验段入口温度相差40 ℃时,关闭泵和阀门6并打开阀门5,让整个回路建立起自然循环单相稳态流动。

表3 实验参数运行范围Table 3 Operation range of experimental parameter
2) 两相不稳定态
在所建立的自然循环单相稳态流动的基础上,保持预期的实验段入口过冷度不变,逐渐升高实验段的热流密度直至出现流动不稳定振荡。待系统压力等参数波动变得规律后才开始记录。因为自然循环中各种热工参数互相耦合,当改变热流密度时,系统需要一定的时间来达到新的稳定的过程,所以记录时间大于振荡周期20倍以上。重复以上步骤,完成不同系统压力、不同入口过冷度和不同稳压器位置的OFI实验。
2 实验结果和分析
2.1 实验值与经验关系式计算值的对比
在OFI研究中,很多学者提出了一些经验公式用以计算OFI对应的热流密度(表4)。表中,qsat为流体达到饱和时所对应的热流密度(kW/m2),计算公式如下:
qsat=cpG(Tsat-Tin)
(1)
其中:cp为比热容,kJ/(kg·℃);G为质量流速,kg/(m2·s);Tsat为饱和温度,℃;Tin为入口温度,℃。

表4 qOFI经验计算公式Table 4 Empirical equation of qOFI

图3 qOFI实验值和其他3个经验关系式计算值的比较Fig.3 Comparison of experimental qOFI with three other empirical equations qOFI
通过其他学者的经验公式计算获得的qsat和本实验结果的对比如图3所示。图中,虚线表示实验值和计算值相等。Xu等经验公式的实验条件与本实验最为接近,但计算误差仍很大。在30 ℃以上的过冷度下最大相对误差为58.48%,过冷度为10 ℃时最大相对误差达179.75%。由于其他学者获得的经验公式与本实验中的自然循环棒束形通道条件差别很大,且都是强迫循环下获得的实验结果,计算值和实验值最大相对误差达到了266.48%。因此这些经验公式对本实验条件并不适用。
2.2 本实验台经验关系式拟合
将本实验中获得的实验数据进行拟合,可得到自然循环棒束形通道OFI所对应的经验公式:
(2)
通过此经验公式获得的计算结果的最大相对误差为20.10%(图4)。由式(1)可知,qsat的计算公式中包括了入口过冷度和质量流速两个因素,因此式(2)也很好地反映了这两个因素对OFI的影响。在核反应堆堆芯的多棒束形通道中,棒束形通道的外表面并不具有像本实验中的棒束形通道外的正方形盒。因此本实验中的流动阻力更大,进而使得自然循环回路的流量偏小,由本实验的经验公式计算得到的qOFI偏小。在将本经验公式运用到多棒束形通道时应加以修正。

图4 qOFI实验值和计算值的比较Fig.4 Comparison of experimental qOFI with calculated qOFI
3 RELAP5计算结果和分析
3.1 RELAP5数值模拟建模
根据图1中的实验台数据,用RELAP5对其进行数值模拟建模,拓宽自然循环棒束形通道研究范围。若无特别强调,均认为稳压器连接在棒束形通道下游,数值模拟建模如图5所示。图中,PIPE 200为棒束形加热通道,即加热段;SNGLVOL 110为加热段的下封头,SNGLVOL 250为加热段的上封头;PIPE 100和PIPE 300为加热段附近的水平段;PIPE 320、PIPE 340、PIPE 360和SNGLVOL 250为上升段;PIPE 720、PIPE 740和SNGLVOL 110为入口段;PIPE 560和PIPE 600为下降段;PIPE 940为稳压器,其出口处用时间控制体TMDPVOL 960控制压力;PIPE 680为预热器;PIPE 780和PIPE 500为冷凝器,其进出口分别用时间控制体TMDPVOL 760和TMDPVOL 800控制压力和温度等。加热段、预热段和冷凝器的热交换部分用热构件HEAT STRUCTURE来建模。热构件需定义沿径向和轴向的节点分布,如图5所示。同时还需定义其左右边界和功率。

图5 RELAP5建模示意图Fig.5 Schematic of RELAP5 model
3.2 节点数对热工水力参数的影响
整个系统的节点数可能会对计算结果造成影响[15],为选择合理的节点数,在建模初期对每个控制体进行了节点无关性分析,系统总节点数对热工水力参数的影响如图6所示。RELAP5计算结果表明,在整个系统节点数为421以后,加热段入口处的温度和流量几乎不变,均为定值。考虑到进一步增加系统总节点数对计算结果影响很小,却会造成计算时间增大,所以最后选定自然循环棒束形通道整个系统的节点数为421。
3.3 RELAP5建模正确性验证
为验证RELAP5建模的正确性,将0.5 MPa工况下的实验结果和RELAP5计算结果进行对比,结果列于表5,在给定预热器加热功率、实验加热段功率和系统压力情况下,通过调节冷凝器二次侧流量达到入口过冷度目标值。由表5可见,实验结果和RELAP5计算结果吻合很好,流量的最大相对误差为2.5%。温度的相对误差很小,最大值为0.98%。因此可认为本模型是准确的。
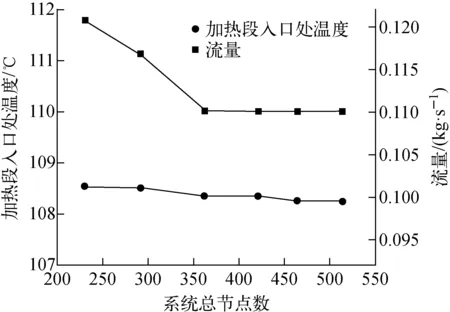
图6 系统总节点数对热工水力参数的影响Fig.6 Effect of total node number on thermal hydraulic parameter

表5 本文实验结果和RELAP5计算结果对比Table 5 Comparison of experimental and RELAP5 results
3.4 OFI热流密度计算结果
给定系统压力和入口过冷度,逐渐提高加热段的热流密度直到产生流动不稳定性现象,通过实验和RELAP5数值模拟计算得到了3组自然循环工况条件下的OFI热流密度(表6)。RELAP5计算结果均大于实验值,说明RELAP5对于OFI计算结果更不保守。RELAP5计算结果和实验结果在入口过冷度为50 ℃时,对应的误差较小,最大相对误差为3.17%;在入口过冷度为30 ℃时,相对误差为31.81%。因此,RELAP5对于OFI热流密度的计算结果可作为参考,但需注意其计算结果更不保守。

表6 OFI热流密度实验值和RELAP5计算值的比较Table 6 Comparison of OFI heat flux of RELAP5 and experiment
3.5 OFI驱动力分析
在闪蒸的研究中,认为长直上升段中会因为静压头减小,从加热段进入到上升段的流体温度达到当地的饱和温度,从而使得上升段中产生闪蒸现象,产生大量气泡[16]。在有关文献[16]中提出将自然循环驱动力分为加热段驱动力和上升段驱动力来分析相应的振荡现象。与本实验台不同的是,在本实验台模型中,由于入口段和下降段之间还存在着预热器,所以入口段和下降段的密度也是不同的。因此,自然循环的驱动力除上述两种驱动力外,还应考虑入口段提供的驱动力。驱动力计算公式为:
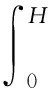
(3)
式中:Ftotal为总的自然循环驱动力,kPa;H为下降段高度,m;ρr、ρh、ρin、ρd分别为上升段、加热段、入口段、下降段内的流体密度,kg/m3。
图7为热流密度升高过程中棒束形通道内流动从稳态过渡到不稳定态的振荡过程,对应的系统压力为0.5 MPa,入口过冷度为30 ℃。在10 000 s之前,棒束形通道的热流密度为103.16 kW/m2;随后,热流密度在10 s内逐渐升高到110.52 kW/m2。自然循环系统内流体的流动由冷热段的密度差来驱动,从图7可知,在10 000 s之后,由于驱动力的突然改变,使得流量也随之改变。两者均开始发生振荡。
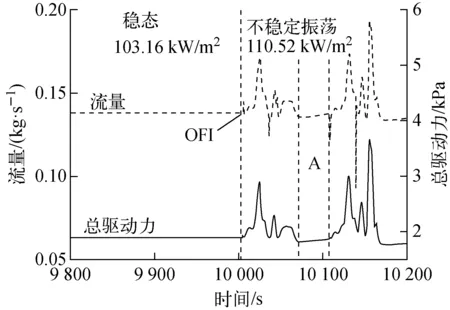
图7 流量和总驱动力振荡Fig.7 Mass flow rate and total driving force oscillation
热流密度升高,使得加热段和上升段内流体温度升高,进而使总驱动力上升。但OFI对应的热流密度仍相对较小,难以维持周期规律性的振荡。驱动力在振荡过程中,中间仍存在着一段低水平(约1.0 kPa)的区域,相对应的此区域的流量也处在较低水平,如图7中区域A所示。在低流速和恒定的热流密度作用下,热段的温度上升,驱动力也逐渐增大,流量随之开始产生新的振荡。
热流密度增大时,加热段出口处流体的主流温度升高,逐渐接近出口处的饱和温度,如图8所示。通过计算可知,此时靠近棒束形通道加热段壁面处的流体温度为152.85 ℃,已超过当地饱和温度,因此此时靠近棒束壁面处的流体已产生了过冷沸腾。过冷沸腾作用产生了气泡,使得冷热段的密度差大幅增大,进而促使总驱动力迅速增大。最终使得流量也随之迅速增大,物理现象则表现为流量振荡。

图8 加热段出口处的主流温度和饱和温度Fig.8 Saturation and average temperatures of heated section outlet
RELAP5程序采用Saha-Zuber模型计算净蒸汽产生点,而Saha和Zuber在最初研究此模型时用到的大量实验数据多为高压条件,且低压条件下的结果相对误差约为±25%[17]。棒束形加热通道内的气泡产生直接影响了OFI,这也使得低压条件下实验结果和RELAP5计算结果得到的OFI热流密度有偏差(表6)。可在此模型的基础上,针对低压条件增加1个修正因子,从而使RELAP5对于低压条件的适用性更好。
4 结论
本文针对自然循环条件下棒束形通道OFI进行了实验和数值模拟研究。通过实验方法获得了相应的经验公式,运用RELAP5数值模拟方法分析了OFI产生的原因,得出如下结论。
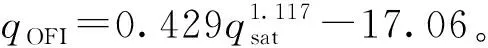
2) 棒束形通道加热段出口处因过冷沸腾产生的气泡,使冷热段的密度差大幅增大,促使了OFI的产生。
3) RELAP5对低压自然循环条件下棒束形通道OFI的适用性好,但RELAP5计算结果较实验结果略不保守。
