考虑风光不确定性的分布式能源集成虚拟电厂收益-风险均衡模型

王 尧，樊 伟，王佳伟，李 强，邢亚虹，魏宏阳，谭忠富

（1.华北电力大学 能源经济与环境研究所，北京 102206；2.国网山西省电力公司 电力经济技术研究院，山西 太原 030002；3.国核电力设计研究院有限公司，北京 100095）

0 引言

风电、光伏具有波动性、随机性等特点，难以实现多区域大规模的利用[1]，[2]。虚拟电厂（Virtual Power Plant，VPP）利用先进的信息网络系统，将分布式电源、储能单元和受控负荷聚合，实现大范围内的能源互联与共享[3]～[7]。研究VPP 最优运行策略对于促进分布式能源的规模化利用有着重要的意义。

当前，已有部分成果涉及到VPP 运行的不确定性问题。电力市场的电价具有不确定性特征，虚拟电厂参与市场竞标时须要处理不确定性因素的影响，文献[8]应用鲁棒优化的方法处理电力市场电价的不确定性。文献[9]提出一种关于大扰动时紧急功率控制的双模式优化控制方案，来应对生物质发电的波动性。文献[10]基于区间分析法，分析风电、负荷等区间的不确定性对虚拟发电厂的影响。文献[11]采用概率价格的机组组合方法，利用点估计法对市场价格和发电源的不确定性进行建模，对未来一天电力市场中虚拟电厂的最优竞价进行建模。文献[12]通过描述常规机组的鲁棒运行轨迹来应对风电不确定性。文献[13]～[15]分别运用了鲁棒随机优化理论和条件风险价值理论，描述风光出力的不确定性。为了避免市场价格不确定性带来的利润波动，基于条件风险价值和二阶随机优势约束的理论方法，能够在VPP 决策问题中实现两种有效的风险管理方法[16]。文献[17]针对风电场（Wind Power Plant，WPP）和光伏发电站（Photovoltaic，PV），提出了一种具有双重鲁棒系数的双层鲁棒调度模型。上述文献更多的采用概率方式表征不确定性，但容量较小、 对数量巨大的DERs 是否具有统计性质仍有待验证。此外，不确定性处理方法主要依赖随机规划方法，须考虑不确定因素的概率分布，但其概率分布规律很难准确描述。

基于上述分析，本文将WPP，PV，小水电站（Small Hydropower Station，SHS）、燃气轮机（Convention Gas Turbine，CGT）、 价格型需求响应（Price-Based Demand Response，PBDR） 负荷及激励型需求响应（Incentive-Based Demand Response，IBDR）负荷集成为虚拟电厂，并利用鲁棒随机优化理论和条件风险价值方法描述风光不确定性风险，构造VPP 风险规避优化模型，并对所提模型进行实例分析，为VPP 最优化运行提供决策支撑。

1 虚拟电厂基本结构

1.1 虚拟电厂结构

为充分利用分布式能源，本文将WPP，PV，SHS，CGT，ESS，PBDR及IBDR集成为VPP。VPP根据终端用户负荷需求和不同分布式电源可用出力，制定最优的调度优化策略。为提升VPP 自身的调节特性，设定SHS 带有年调节水平，即能够根据WPP 和PV 的实际可用出力，通过调整水库蓄水量，参与到VPP 发电调度中。虚拟电厂的基本结构如图1 所示。

图1 虚拟电厂基本结构Fig.1 Basic structure of virtual power plant

图中 WPP，PV 和 CGT 为主要的电源，剩余负荷需求则由SHS满足，IBDR、ESS用于为WPP，PV 提供备用服务。

1.2 电源出力模型

（1）WPP 和 PV 发电出力模型

本文采用Rayleigh 分布函数和Beta 分布函数用于计算WPP 和PV 发电出力，其表达式为

式中：gR为WPP的额定功率；νin，νR，νout为WPP的切入、额定和切出风速；νt为WPP在时刻t的实时风速；g*WPP，t为WPP在时刻t的可用出力；g*PV，t为PV在时刻 t 的最大出力；ηPV，SPV为太阳能辐射效率和采光面积；θt为在时刻t的太阳能辐射强度。

（2）SHS 发电出力模型

水电站出力模型为

（3）ESS 运行模型

引入荷电状态（State of Charge，SOC），用于描述蓄电池剩余电力与其总容量的比例，确立ESS的净出力功率为

式中：gESS，t为 ESS 在时刻 t 的净充放电功率；uch，udis分别为ESS 的充、放电状态变量。

1.3 需求响应模型

（1） PBDR 负荷计算模型

价格型需求响应可以实现负荷曲线的 “削峰填谷”。在获得电力价格弹性矩阵后，PBDR 对负荷需求的影响为

（2）IBDR 负荷计算模型

IBDR 主要由需求响应供应商根据出力价格分步提供，可用于能源市场调度和储备市场调度，DRPs 参与能源市场负荷削减关系为

2 VPP常规调度优化模型

2.1 目标函数

为实现运营期望值收益最大，建立含WPP，PV，SHS 的 VPP 数学模型为

式中：gVPP为VPP的电能输出功率；N（·）为VPP的运营净收益；R（·）和C（·）分别为VPP的运营收入和成本；RWPP，t，RPV，t，RSHS，t，RCGT，t，RESS，t和RIBDR，t分别为WPP，PV，SHS，CGT，ESS和IBDR在时刻t的运营收益；PESS，tdis和PESS，tch分别为ESS在时刻t的充放电价格；gESS，tdis和gESS，tch分别为ESS在时刻t的充放电电量；Pi，tj为DRPi在步骤j时刻t的价格；CCGT，t和CSHS，t分别为CGT和SHS在时刻t的运营成本；aCGT，bCGT和cCGT分别为CGT发电能耗系数；uCGT，t为CGT发电状态变量，其值为0～1变量；NCGThot，NCGTcold分别为CGT发电热启动和冷启动成本；TCGTmin为CGT最小启动时间；TCGToff为CGT持续停机时间；TCGTcold为CGT冷启动需求时间。

2.2 约束条件

（1）负荷供需平衡约束

式中：φWPP，φPV，φCGT分别为能源利用效率；ΔLIB，tE为IBDR在时刻t能源市场出力；uIB，t和uPB，t为IBDR和PBDR状态变量；ΔLPB，t为PBDR在时刻t产生的负荷变量。

（2）SHS 运行约束

水库需水量、发电引流量以及弃水量约束为

式中：VT0-1为任意时段开始前调节水库需水量；Vmin为允许水库消落的最低库容量；Vmax为允许水库可用最大水量；qt，Qt，St分别为水电站在时刻 t的自然来水量、 发电引流量以及弃水流量；Qmin，Qmax分别为水电站水轮机发电引流量的最小、最大值；Smin，Smax分别为 SHS 允许弃水量的最小、最大值。

（3）其他发电出力约束

CGT，IBDR 主要须满足最大和最小功率约束、启停时间约束和上下爬坡约束。ESS 须满足最大充放电功率约束、充放电状态约束等。PBDR 所产生的出力同样须要满足各时刻最大出力约束、上下爬坡约束和累计最大出力约束等。CGT 机组约束条件为

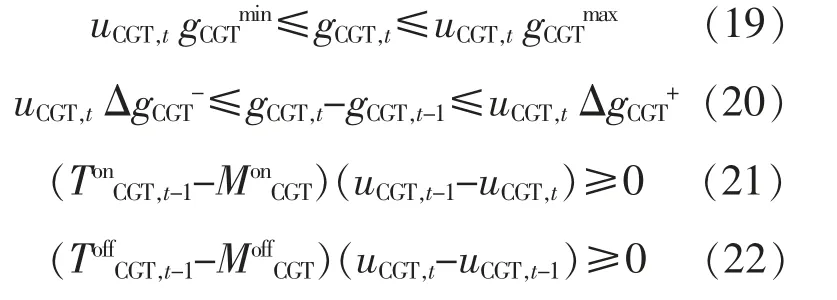
式中：gCGTmax，gCGTmin分别为 CGT 发电出力上、下限；ΔgCGT+，ΔgCGT-为 CGT 爬坡上、下限；TonCGT，t-1为 CGT在时刻t 的持续运行时间；MonCGT为CGT 最短启动时间；ToffCGT，t-1为 CGT 在时刻 t 的持续停机时间；MoffCGT为CGT 最短停机时间.

（4）系统旋转备用约束

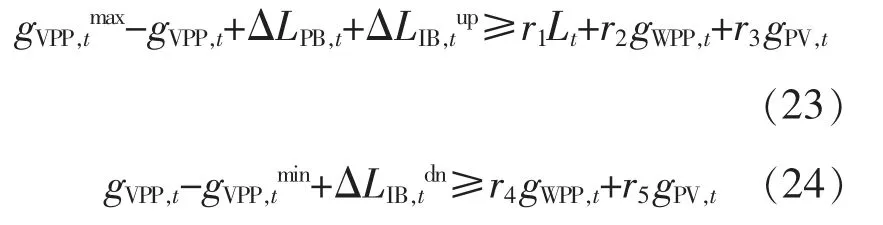
式中：gVPP，tmax，gVPP，tmin分别为 VPP 在时刻 t的最大、最小可用出力，此时，CGT 机组分别处于最大功率、 最小功率；gVPP，t为 VPP 在时刻 t 的发电功率；ΔLPB，t为 PBDR 在时刻 t 提供的负荷变化量；r1，r2，r3分别为负荷、WPP、PV 的上旋转备用系数；r4，r5分别为WPP，PV 的下旋转备用系数。

3 VPP风险规避优化模型

WPP，PV 的随机性导致VPP 运行具有不确定性。准确评估VPP 运行的不确定性及其风险是制定最优VPP 运行策略的关键。Value at Risk（VaR）算法通常可估计定量分析风险特性，但只能测算给定置信水平下的风险状况、不能测算风险尾部的情况，存在一定的局限性。Conditional Value at Risk （CVaR）能够估计置信水平外的风险情况。

为了充分考虑不确定性给VPP 带来的运行风险，本文应用CVaR 理论表征VPP 调度运行风险特性。考虑不确定性后的虚拟电厂CVaR 函数调度为

式中： α 为决策者风险判定的门槛值；β 为 VPP运行目标函数的置信度。

当式（25）达到最小时，即为CVaR 值，此时α就是VaR 值。为了确保WPP 和PV 实际出力达到边界时，仍满足约束条件，引入辅助变量 θRE，t（θ≥0），并设定为了增加模型灵活性，引入鲁棒系数 Г，Г∈[0，1]，上述约束条件为

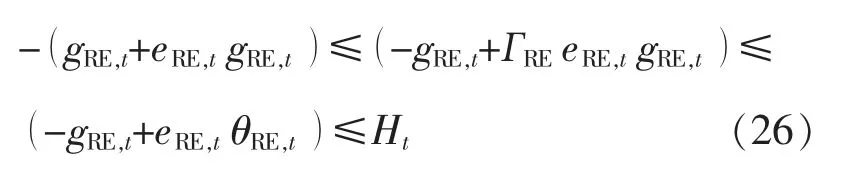
最终，结合式（17）～（22），（26）及目标函数，建立VPP 风险规避优化模型为

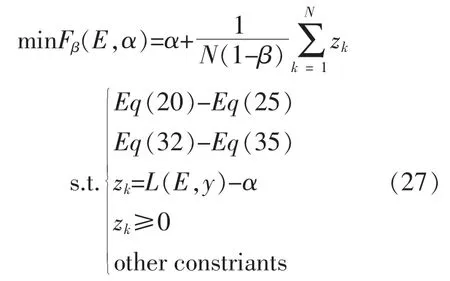
综上，在系统运行信息掌握不完全情况下，本文所提风险规避模型能够在一定扰动范围内保证系统安全、稳定运行，提高系统对不确定性因素的免疫能力，并实现调度预定目标。

4 算例分析

4.1 基础数据

为验证所提模型的有效性和适用性，本文选择我国东部沿海独立工业园区微电网进行实例分析。该园区配置 WPP 为 2×0.25 MW，PV 为 4×0.1 MW，CGT 为 1×1 MW，ESS 为 1×0.2 MW·h，SHS配置5×50 kW 的小型水利发电机组。水电机组每年平均水流量为40 m3/h，调节水库最大库容为9×104m3，调节水库初始的水量是最大水库容量的70%，发电用水价格参照文献[10]选取。CGT 主要选取G3406LE 型燃气轮机，额定输出功率为1.025 MW，天然气消耗量为107.7 m3/h。该型号燃气轮机启动和停机时间分别为0.1，0.2 h，启停成本约为 95 元/（MW·h），发电燃气成本为一元二次函数，具体参数参照文献[15]设定。同时，为了便于求解，将发电成本函数线性化为两段，两段的斜率系数分别是105 元/MW 和355 元/MW，机组发电损耗约为2.5%。其中，储能系统充电功率不超过0.04 MW，放电功率不超过0.05 MW，ESS 初始蓄电量为0[6]。同时，为保障储能的安全可靠运行，限定ESS 不能同时充放电。

图3 为冬季和夏季典型负荷日数据。

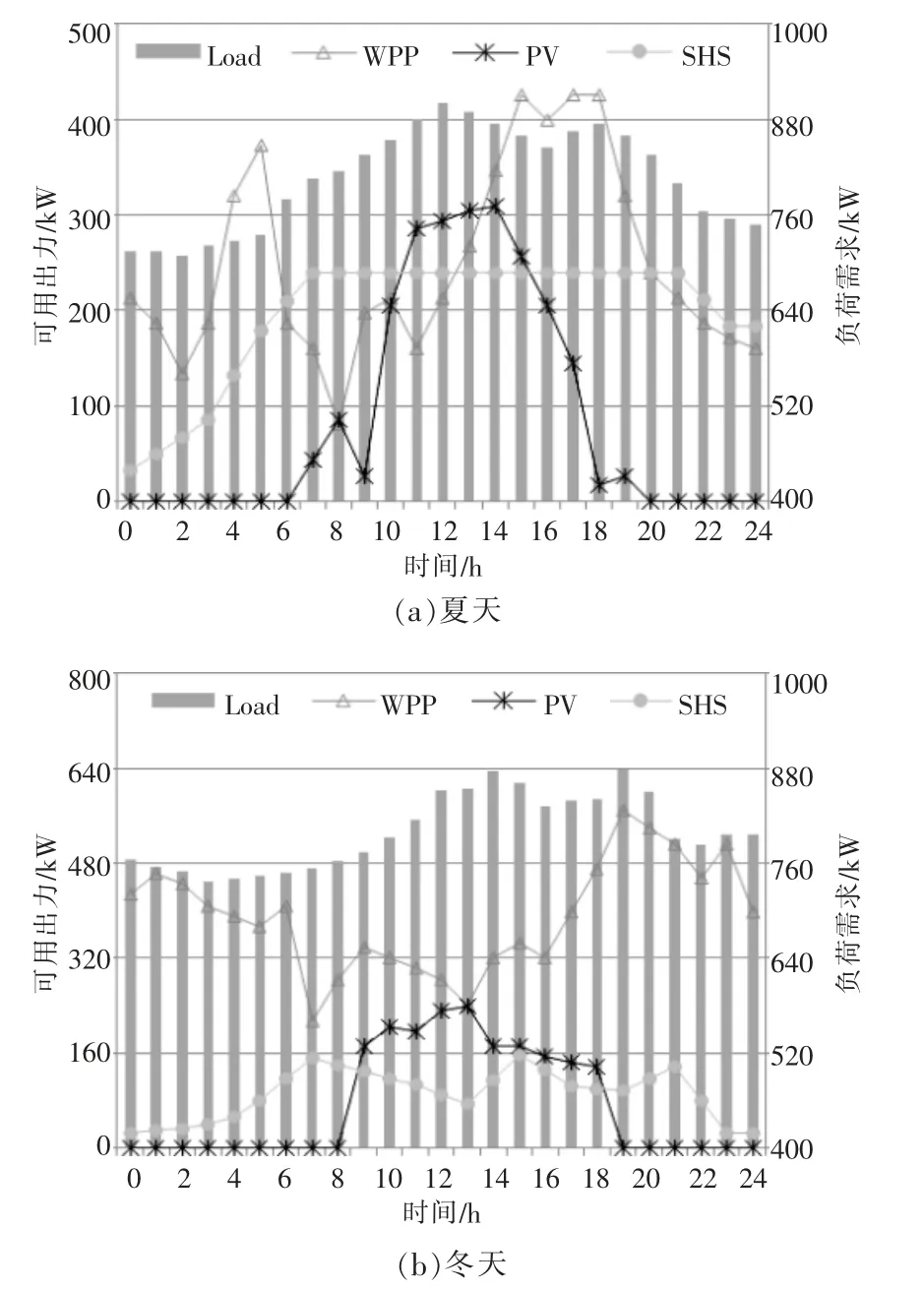
图3 负荷需求和可用出力Fig.3 Load demand and available output in typical load day

设定WPP 切入、 切出和额定风速分别为2.80，22.8 m/s 和 12.5 m/s，其中形状参数 φ=2，尺度参数设定太阳能辐射密度参数φ 和 θ 分别为 0.3 和 8.54，WPP 和 PV 预测误差为5%。园区 WPP，PV，SHS，CGT 上网标杆电价分别为0.51，0.88，0.31，0.42 元/（kW·h）。同时，为激励终端用户响应系统发电调度，设定PBDR 前用户的用电价格为 0.59 元/（kW·h）。参照文献[2]选取电力需求价格弹性，并设定平时段价格不变，峰时段用电价格上调30%，谷时段用电价格下调50%。对于IBDR 来说，在能量市场提供能源价格为 0.45 元/（kW·h）。同时，为了避免负荷波动过大，出现“峰谷倒挂”的现象，假定PBDR 引起的负荷变动不超过±0.04 MW，IBDR 的发电出力不超过±0.03 MW。表1为 IBDR 和 PBDR 的运营参数。

表1 为IBDR 和PBDR 的运营参数Table 1 Parameters of PBDR and IBDR in typical load day

4.2 算例结果

（1）不考虑不确定性VPP 运行结果

该情景重点分析 VPP 中 WPP，PV 和 SHS 间的互补效应。从负荷需求来看，在冬季典型负荷日，夜间采暖需求较大，白天采暖需求少，故峰谷差较低。在夏季典型负荷日，由于白天制冷需求较大，夜间制冷需求较小，故峰谷差相对较高。图4为典型负荷日VPP 发电出力分布。

图4 典型负荷日VPP 发电出力分布Fig.4 Output distribution of VPP power generation in typical day

由图4 可知，在夏季典型负荷日，负荷主要由CGT 和SHS 满足，剩余负荷由WPP 满足。在冬季典型负荷日，负荷主要由CGT 和WPP 满足，剩余负荷则由SHS 满足。在不同典型负荷日不同电源间存在着显著的互补效应。VPP 能够通过聚合不同分布式电源，形成稳定发电出力以满足用户负荷需求，从而获得最大的运营收益。表2，3 为不同典型负荷日VPP 调度运营结果。

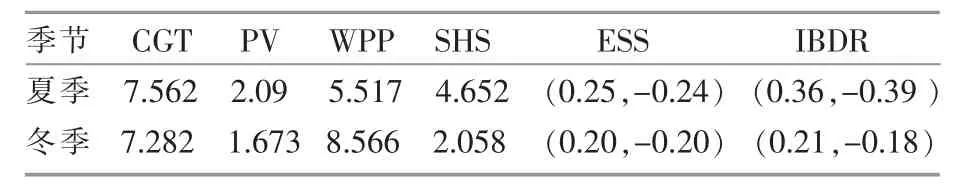
表2 典型负荷日VPP 运行出力结果Table 2 Output results of VPP operation in typical load day MW·h

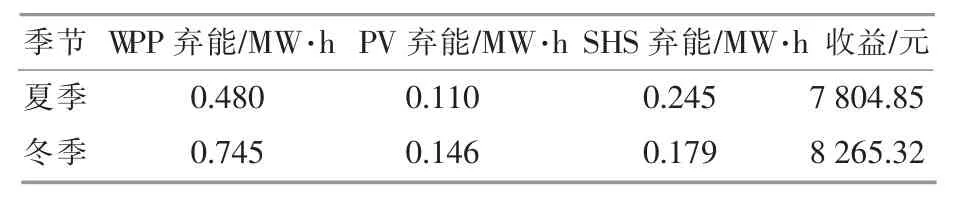
表3 典型负荷日VPP 运行调度结果Table 3 Scheduling results of VPP operation in typical load day

由表2 可知，在不考虑不确定性风险时，为追求最大化的运营收益，VPP 会优先利用清洁能源发电满足负荷需求，WPP，PV，SHS 在夏季和冬季典型负荷日的总出力分别为 12.259，12.297 MW·h。相应的夏季典型负荷日，VPP 运营收益要低于冬季460.47 元。由于夏季典型负荷日的峰谷比要高于冬季，因而CGT，ESS 和IBDR 的出力也相对较高。

（2）考虑不确定性VPP 运行结果

该情景分析不确定性对VPP 运行的影响，设定初始鲁棒系数Γ=0.9，确立VPP 的最优调度策略。在夏季典型负荷日，WPP，PV，SHS 的总并网电量分别为 4.797，1.760，4.407 MW·h；在冬季典型负荷日，WPP，PV，SHS 的总并网电量分别为6.984，1.455，1.901 MW·h。可见，当考虑约束条件中不确定性变量时，决策者对风险的敏感度有所增加，为了规避VPP 运营风险，决策者会降低WPP 和 PV 发电出力。

图5 为典型负荷日VPP 发电出力分布。由图5 可知，引入鲁棒随机优化理论后，VPP 会压缩WPP 和 PV 的并网空间。夏季典型负荷日WPP 和 PV 出力降低了 0.11 MW·h 和 0.307 MW·h。然而，CGT 因其出力可控，更多的被VPP 调用，增加 0.431 MW·h。同样，WPP 和 PV发电出力的降低，导致 ESS 和IBDR 的出力也有所降低，仅在峰时段调用ESS 放电释能和IBDR 减少出力，在谷时段调用ESS 充电蓄能和IBDR 增加负荷。

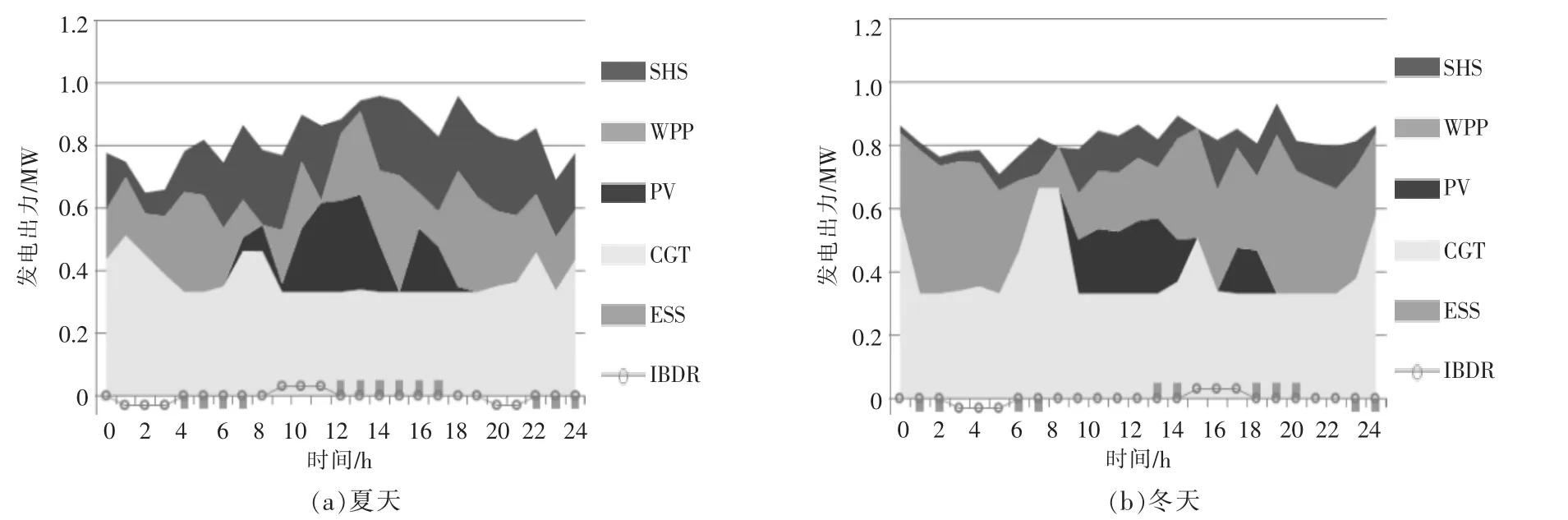
图5 典型负荷日VPP 发电出力分布Fig.5 Output distribution of VPP power generation in typical day

表4，5 分别为不同情景下VPP 运行出力和调度优化结果。

表4 不同情景下VPP 运行出力结果Table 4 Output results of VPP operation in different scenarios

表5 不同情景下VPP 运行调度结果Table 5 Scheduling results of VPP operation in different scenarios

由表5可知，当考虑不确定性时，WPP，PV 的风险将被纳入优化目标，决策者会控制WPP，PV的出力，VPP 运营收益降低，但同样的置信度β下的VaR 和CVaR 值增加，表明收益和风险相互联系，决策者在追求高额经济收益的同时也须要承担相应的风险水平。反之，当决策者想要规避风险时，将要舍弃部分经济收益。

由于约束条件中不确定性通过预测误差和鲁棒系数进行描述，也能够直接影响VPP 的优化运行，故对预测误差e、鲁棒系数Г 和置信度β 间的相互关系进行敏感性分析，讨论不同参数组合下的VPP 运行方案。

图6 为不同参数下VPP 运营收益和发电出力。由图6 可知，当e 较高时，相同增长幅度会导致 CvaR 增长更快，当预测误差 e∈[5%，10%），CVaR 增长幅度要低于e∈[15%，25%）。当预测精度降低时，不确定性因素给VPP 运行带来的风险要较高。当 Γ≤0.85 时，β 增长会导致 CVaR 增长幅度较大，表明当决策者考虑不确定性时，VPP运营方案会发生显著变动。当 Γ∈（0.85，0.95），β增长带来的CVaR 增长幅度较低，决策者会均衡VPP 运营收益和风险，故决策方案处于相对稳定状态，但整体上CVaR 值也会随Γ 的增加而增加。当 Γ≥0.95，β 的增长带来的 CVaR 增长幅度很大，较小的不确定性都会带来较大的运营风险。综上CVaR 方法和鲁棒随机优化理论能够更好地描述VPP 运行的不确定性风险，决策者在提升不确定性预测精度的同时，须设置合理的置信度和鲁棒系数，兼顾VPP 运行风险和收益。

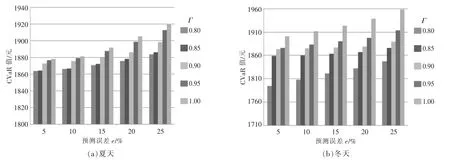
图6 不同参数下VPP 运营收益和发电出力（冬季典型负荷日）Fig.6 The CVaR values of VPP operation under different β，and e （Winter typical day）

5 结论

为了充分利用分布式可再生能源，本文将WPP，PV，SHS，ESS，PBDR 和 IBDR 集成为 VPP。为应对WPP 和PV 给VPP 带来的不确定性，本文构建了基于CVaR 方法和鲁棒随机优化理论的VPP 随机调度优化模型。算例分析表明：①夏季峰谷差较大，PV，SHS 和 CGT 为主要电源，特别是带有年调节水库的SHS 能为WPP 和PV 提供备用服务。冬季负荷峰谷差较低，WPP 和CGT 为主要电源。ESS，IBDR 和 CGT 能为 WPP，PV 提供备用服务，在最大化利用可再生能源的同时取得最大化的经济收益，实现整体VPP 最优均衡运行；②所提VPP 风险规避模型能够有效应对WPP 和PV 所带来的运营风险。CvaR 方法和鲁棒随机优化理论能够描述不确定性因素所带来的风险；③置信度和鲁棒系数是VPP 最优运行的关键因素，当预测误差e 较高时，Γ 增长相同幅度会带来CVaR 更大幅度的增长，表明较低的预测精度会放大不确定性风险。为实现VPP 最优化运行，决策者须在提升预测精度的同时，设置合理的置信度和鲁棒系数，以制定最优的风险控制策略。