大规模风电外送系统FACTS优化配置

赵树野，王俊生，陈庆珠，党 伟，赵立军，孙 碣，黄南天

（1.国网内蒙古东部电力有限公司 经济技术研究院，内蒙古 呼和浩特 010020；2.东北电力大学 电气工程学院，吉林 吉林 132012；3.国网经济技术研究院有限公司 蒙东分公司，内蒙古 呼和浩特 010020）

0 引言

近些年，我国可再生能源行业发展迅速，风电装机容量超过200 GW[1]。目前，我国的风电场大多集中于东北地区、西北地区和华北北部地区（简称“三北”地区），这些地区就地消纳风电的能力有限，须建设超高压跨区输电通道或特高压跨区输电通道，来提高风电等大规模可再生能源的消纳能力[2]。

由于风电等可再生能源的出力存在随机性和波动性，使得超高压、特高压输电通道上的潮流频繁变化，输电网电压的控制难度也较高，从而影响电力系统的输电能力。本文应用柔性交流输电（Flexible AC Transmission System，FACTS）设备提高电网的输电能力以及电网运行的稳定性。FACTS 设备以电力电子设备为基础，并结合了现代控制技术。将该设备应用于高压输电系统，能够对交流输电系统的相关参数及其网络结构进行灵活控制，从而大幅提高电力系统的可用输电能力[3]。

在FACTS 设备的配置过程中，若安装地点、类型、容量等不合理，会降低电力系统的输电能力和电压稳定性，进而造成投资成本的升高。为了实现FACTS 设备的优化配置，国内外学者针对FACTS 设备的选址和定容问题进行了大量研究。文献[4]对电力系统的可用输电能力和FACTS 设备的投资成本进行了优化配置研究，该研究过程中未考虑大规模可再生能源外送时输电网电压的剧烈波动问题。文献[5]先基于灵敏度分析法确定FACTS 设备的安装位置，然后使用期望容量指标确定FACTS 设备的容量，即分两个阶段多次协调FACTS 设备的安装地点和容量。该配置方法虽有一定的补偿效果，但未考虑FACTS 设备的安装地点与容量之间的相互影响。文献[6]利用由潮流分析所得的拉格朗日乘子将FACTS 构成的多目标函数加权转化为单目标优化问题，这样虽然简化了求解过程，但存在一定的主观性。文献[7]分别使用遗传算法和粒子群优化算法对FACTS 设备进行优化配置，研究表明粒子群算法对非线性多目标问题求解的准确性较好，但利用该算法对传统PSO 进行局部、全局寻优时，难以实现寻优平衡[8]。目前，对于FACTS 设备的优化配置，取得了较好的研究成果，但研究过程大多基于220 kV 电力系统，这与我国实际大规模可再生能源外送通道的电压存在一定的差异。

本文针对传统FACTS 设备优化配置方法在方案确定过程中易于陷入局部最优的弊端，提出了一种基于自组织映射粒子群算法的FACTS 设备配置方法，并以超高压等级IEEE-14 节点输电系统为例，验证该方法的有效性和先进性。

1 FACTS设备数学模型

1.1 SVC数学模型

静止无功补偿装置 （Static Var Compensator，SVC）通过调整电力系统的无功功率，实现无功功率的动态补偿，抑制输电线路电压的波动，提高电网的输电能力。

SVC 可以被视为可控的无功源，并与母线k相连接。SVC 注入母线k 的无功功率QSVC为

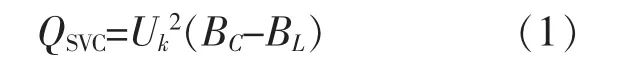
式中：Uk为节点 k 的电压 ；BC，BL分别为固定电容、晶闸管可控电感的电纳。

母线k 的功率平衡方程为

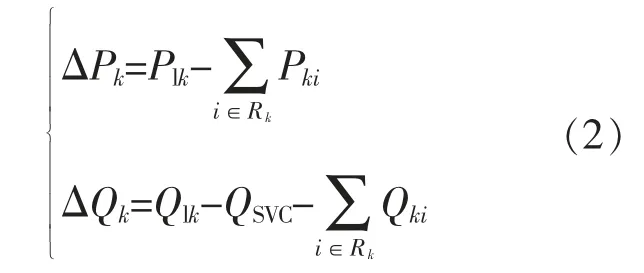
式中：Plk，Qlk分别为 SVC 注入母线 k 的有功、无功负荷；ΔPk，ΔQk分别为母线 k 的有功、 无功负荷的变化量分别为母线k 的有功功率、 无功功率；Rk为与母线k 相连接的线路的个数。

1.2 STATCOM数学模型

静止同步补偿器 （Static Synchronous Compensator，STATCOM）由耦合变压器、逆变器和直流电容器组成，可以对并联无功功率进行补偿。在理想稳态分析过程中，可忽略补偿器与电力系统之间有功功率的交换，则无功源无功功率QS的等效关系式为

式中：QST为FACTS 设备的无功补偿容量。

1.3 TCSC的数学模型

可控串联补偿装置 （Thyristor Controlled Series Compensation，TCSC）与 SVC 相类似，能够提供连续可变的容抗，对交流线路的潮流进行控制。稳定运行状态下，TCSC 可等效为输电线路中串联的可变电抗XT。若节点i，j 之间存在串联的TCSC，则可以忽略较小的对地电纳。

输电线路节点i，j 之间等值电抗的关系式为

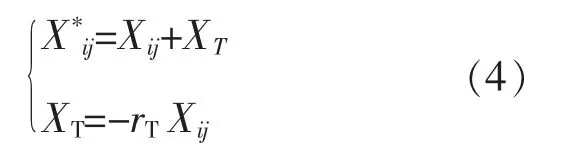
式中：Xij，X*ij分别为补偿前、 后输电线路的电抗；XT，rT分别为 TCSC 的补偿量、补偿度，-0.2≤rT≤0.7。

2 FACTS优化配置数学模型

2.1 目标函数

以输电系统电压稳定性最佳、投资费用最小、可用输电能力最大为目标，建立FACTS 多目标优化配置模型。

2.1.1 可用输电能力

电力系统的可用输电能力（Available Transfer Capability，ATC）为满足热力学、电压、稳定性等约束的电力系统最大传输能力。ATC 的计算方法包括直流潮流算法、 重复电力系统潮流算法和连续潮流算法等。

直流潮流算法的理论方程和计算过程均比较简单，但在传输能力问题中忽略了输电网电压与无功功率耦合的影响，导致计算结果不够准确。重复电力系统潮流算法能够自启动，但计算量高于其他算法。连续潮流算法充分考虑了电压以及电压稳定性的限制，但将该算法应用于电力系统输电能力的计算过程中，会使电力系统的发电量、变压器的抽头位置以及FACTS 的控制等变得难以调节。目前，电力系统传输能力计算的不足之处：未考虑计算过程中基本情况与特殊情况的耦合；未充分考虑无功功率和电压稳定性的影响；计算电力系统的传输能力时，缺少FACTS 装置的模型。针对以上不足，本文采用改进的多目标粒子群算法，并基于潮流分析计算得到电力系统的可用输电能力。

ATC 为最大输电能力与现存输电协议量的差值。计算ATC 时，以传输系统与基态系统之间注入有功功率的增量最大为目标，建立ATC 的计算模型。

ATC 计算模型的表达式为[9]

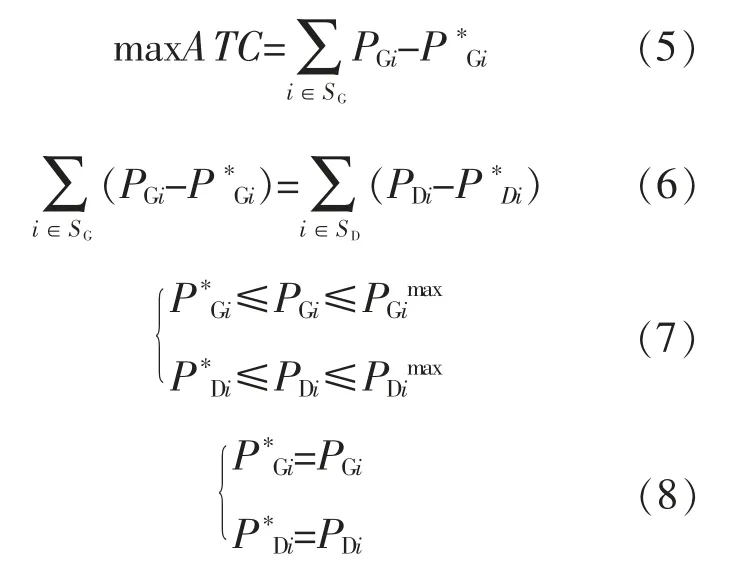
式中：PGi为发电机 i 的注入有功功率；P*Gi，PGimax分别为注入功率的基态值、 上限值；SG为发电节点的总数；PDi为节点i 处所有负荷消耗的有功功率；P*Di，PDimax分别为消耗功率的基态值、上限值；SD为负荷节点的总数。

2.1.2 电压稳定指标

电压稳定性指标（Line Stability Index，LSI）可准确反映电力系统整体的电压波动情况，衡量FACTS 设备配置后电力系统的电压稳定情况。电力系统的二节点支路模型如图1 所示。图中：节点i 处的输出功率 Si=Pi+jQi，送端电压为 Vi∠δi；节点 j 处的注入功率 Sj=Pj+jQj，受端电压为 Vj∠δj。此外，令送、受端电压相角差 δ=δi-δj，支路阻抗 Z=R+jX。

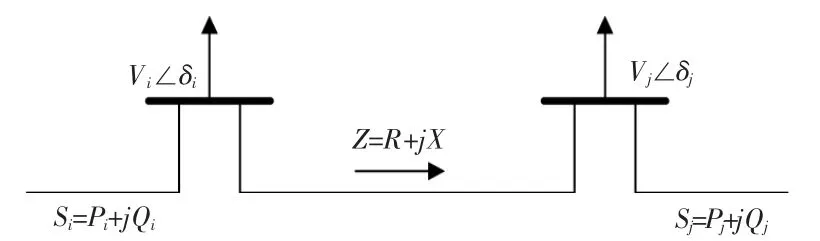
图1 二节点支路模型Fig.1 A branch model for two nodes

基于支路潮流分析得到电压稳定性指标LSI的判定式为[10]

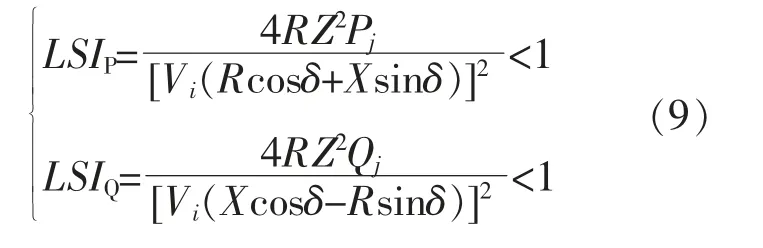
式中：LSIP为基于有功功率的电压稳定指标；LSIQ为基于无功功率的电压稳定指标。

根据 LSIP和 LSIQ得到节点 i，j 之间支路 k 的电压稳定指标LSIk为

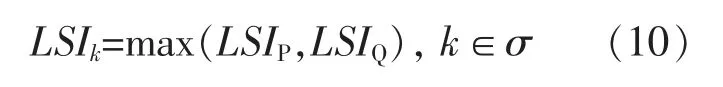
式中：σ 为输电系统支路的数目。

LSI 的取值为0～1，且取值越大，输电系统支路的电压稳定裕度越小，该支路越容易引起电力系统失稳以及输电网电压的崩溃。

若计算出全部支路的LSIk，则可以得到多支路复杂输电系统LSI 的表达式为

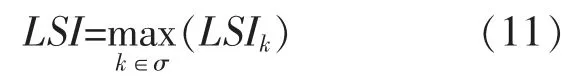
2.1.3 投资费用

FACTS 设备的投资费用与该设备的类型及容量有关。由于FACTS 设备的投资费用比较巨大，因此本文所提出的FACTS 设备配置方法基于较低的投资费用对输电线路的无功功率进行补偿优化。FACTS 设备的投资费用与其容量之间的关系式为[11]

式中：S 为 FACTS 设备的容量；CS，CST，CT分别为SVC，STATCOM，TCSC 单位容量的投资费用。

FACTS 设备总投资JV的计算式为

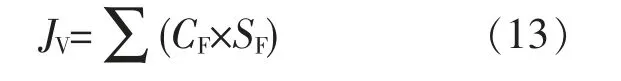
式中：SF为单台 FACTS 设备的运行容量；CF为FACTS 单位容量的投资费用。

2.2 约束条件

2.2.1 功率平衡约束

利用FACTS 设备对输电系统进行优化配置时，传输通道各节点须要满足有功平衡约束和无功平衡约束[12]。有功平衡约束和无功平衡约束的表达式为

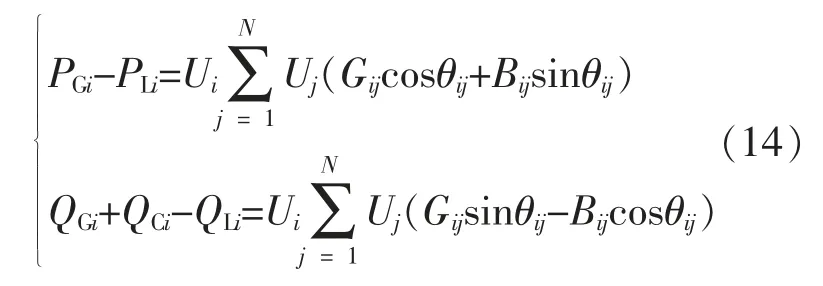
式中：PLi为节点 i 处发电机的有功负荷；QGi，QLi，QCi分别为节点i 处发电机的无功出力、 无功负荷、FACTS 设备输出的无功功率；Gij，Bij分别为节点 i，j 之间的电导、电纳。

2.2.2 不等式约束

电力系统的不等式约束包括控制变量约束和状态变量约束。其中，控制变量约束包括发电机有功出力约束、 发电机无功出力约束、FACTS 补偿容量约束和FACTS 设备容量约束；状态变量约束包括线路传输容量约束、电压越限约束、线路热稳定约束和静态电压稳定约束。上述各约束的表达式分别为

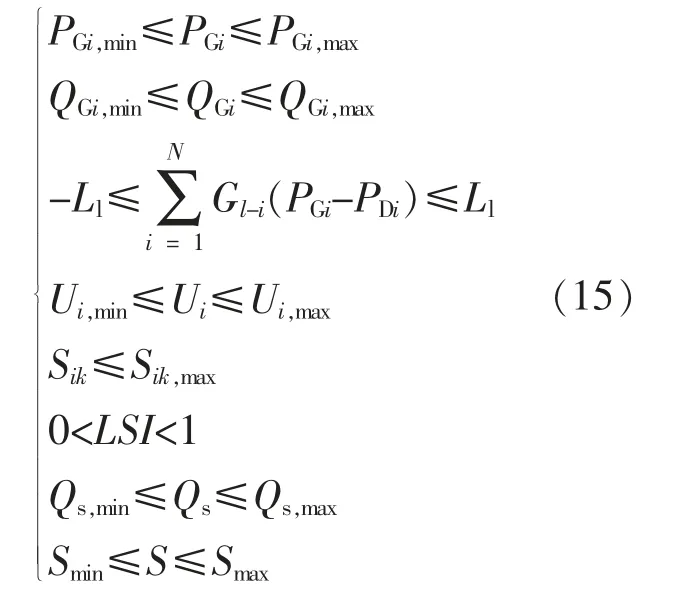
式中：PGi，max，PGi，min分别为节点 i 处注入有功功率的最大、 最小值；QGi，max，QGi，min分别为节点 i 处注入无功功率最大、 最小值；Ll为输电线路传输极限；Gl-i为发电转移因子；Ui，max，Ui，min分别为节点 i 处电压上、 下限；Sik为线路和变压器的视在功率；Sik，max为线路和变压器的热稳定极限功率；Qs，max，Qs，min分别为FACTS 设备注入电网无功功率的最大、最小值；Smax，Smin分别为 FACTS 设备容量的上、下限。

3 基于自组织映射网络算法改进的粒子群优化算法

3.1 多目标优化问题

FACTS 选址定容多目标优化表达式为

式中：h（x）为等式约束，即 FACTS 设备安装后，电力系统的潮流；g（x）为不等式约束，具体的表达式见式（7），（15）。

式（16）中 ATC 与 LSI 前均存在负号，表示这两个目标函数均以最小值为最优值。

FACTS 设备的优化配置可看作为多约束条件下的非线性、多目标最优解计算问题，应用多目标求解算法进行求解。多目标优化问题多在Pareto 解集内寻优后得以解决。Pareto 解集内一般有若干个非劣解，可根据决策需要，选取合适的非劣解作为最优解。

3.2 粒子群算法

多目标粒子群优化算法基于种群随机搜索的全局寻优进化算法，该算法通过模仿鸟类的运动规则，在搜索空间中寻找最优位置。与其他进化算法相似，多目标粒子群优化算法的搜索个体由种群个体组成，这些搜索个体被称为粒子，具体包括位置和速度2 个特征信息。假设当前种群由m 个粒子组成，粒子的搜索范围为n 维超空间，则粒子i∈（1，2，…，m）。此外，令位置信息集合 xi=（xi1，xi2，…，xin），xi反映了配置方案的优化效果；速度信息 νi=（νi1，νi2，…，νin），νi与方案求解所需的时间有关。多目标粒子群优化公式为

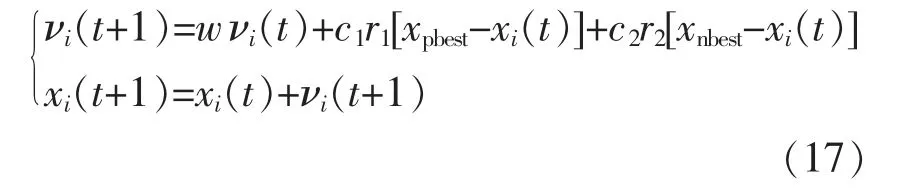
式中：t 为迭代代数；w 为平衡局部搜索和全局搜索的惯性因子；c1，c2均为影响种群收敛速度的学习因子；r1，r2均为 （0，1） 内正态分布产生的随机量；νi（t），νi（t+1）分别为迭代 t 次前、后的粒子速度信息；xi（t），xi（t+1）分别为迭代 t 次前、后的粒子位置信息；xpbest，xnbest分别为全局最优位置信息、局部最优位置信息。

利用多目标粒子群算法进行寻优时，得到的不是唯一的全局最优位置，而是用局部最优位置代替，从而确定全局的较优位置。

3.3 改进粒子群算法

图2 为自组织多目标粒子群算法（SMPSO）的流程图。

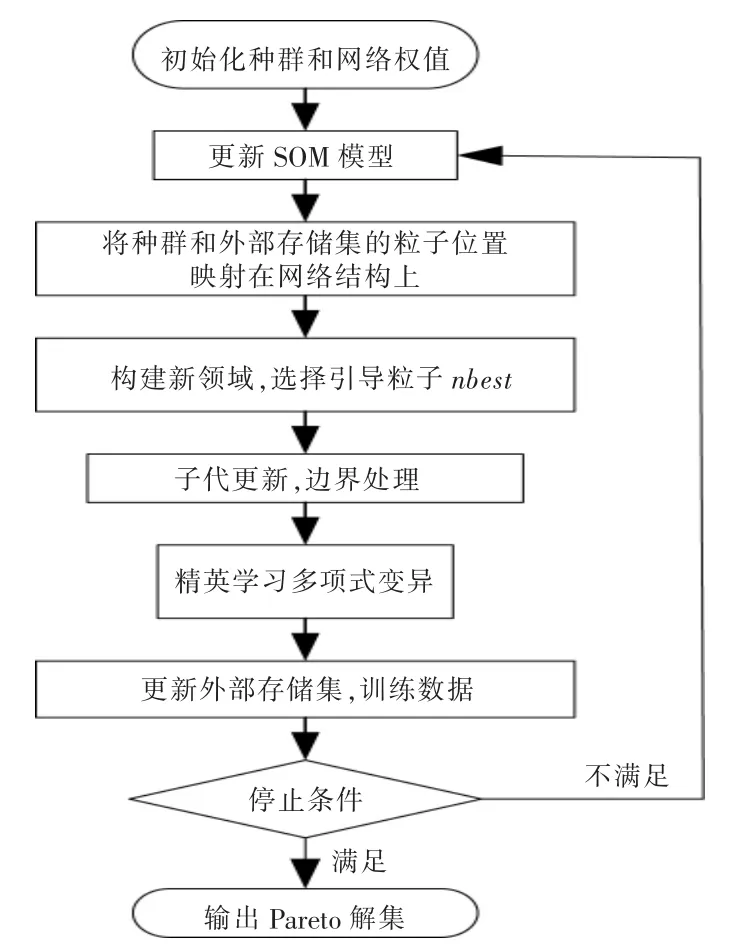
图2 SMPSO 的流程图Fig.2 Algorithm flow chart of SMPSO

由于传统PSO 算法存在解集多样性，以及收敛性难以平衡的不足，因此，本文采用SMPSO 进行寻优，具体的寻优过程：首先，通过自组织映射网络发现种群和Pareto 前沿的结构信息；然后，引导粒子飞行，并加入了精英学习策略以及多项式变异功能，从而丰富了种群的多样性，实现全局寻优。

自组织映射网络 （Self-organizing Mapping Network，SOM） 为基于无监督学习方法的神经网络，可将高维分布函数映射至低维分布函数，并保持映射关系不变。将自组织映射网络与传统多目标粒子群算法结合起来形成SMPSO，在决策空间针对粒子构建了新的邻域关系，使每个粒子能够选取更合适的引导粒子，同时加入精英学习机制，实现解的多样性[13]。由于SOM 能够基于所得的非支配解集进行不断地学习，权值信息也在不断变化，因此，改进算法更有助于解决全局寻优问题。

在SMPSO 计算过程中，当子代更新完毕后，加入精英学习机制。精英学习机制的表达式为

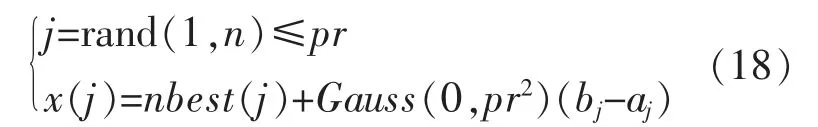
式中：rand（1，n）为 1～n 的随机数；aj，bj分别为粒子 x 第 jth维的上、下界；nbest（j）为第 j 个引导粒子；Gauss（0，pr2）为随机概率模型，其中，0 为随机数的均值，pr 为标准差。

本文中，标准差pr 的取值为0.05～0.2，并且会随着迭代次数的增加而线性减小。为了避免粒子位置陷入局部最优，引入多项式变异，实现粒子的最优位置信息差异化搜索。

4 算例与分析

为了验证本文所采用的设备模型和改进算法对FACTS 优化配置过程的适用性和有效性。以改进的IEEE-14 节点系统为例，进行验证分析。IEEE 标准节点模型的相关参数见文献[14]。

改进的IEEE-14 节点系统的结构图如图3所示。

由图3 可知，本文基于超高压风电外送场景，将IEEE-14 节点输电网络进行分区。A 为输电区域，在此区域加入了风机，总装机容量为300 WM；B，C 为受电区域。FACTS 优化配置的目标为在保证投资经济性和电压稳定性的基础上，提高区域A 与区域B，C 之间的输电能力。

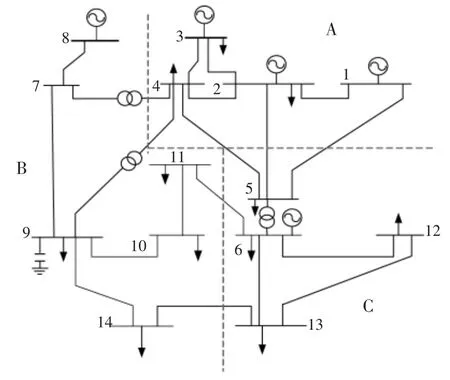
图3 改进的IEEE-14 节点系统的结构图Fig.3 Structural diagram of the improved IEEE-14 bus system

4.1 参数设置

本文算例的相关参数： 基准电压为500 kV，基准功率为100 MV·A，优化算法的迭代次数为200；粒子群算法种群大小NP 为100，PSO 参数的惯性权重w 为0.4，学习因子c1=c2=0.2 （取标准值）；输电系统中PV 节点电压的标幺值为0.9～1.0 pu，PQ 节点电压的标幺值为 0.94～1.06 pu；SVC，STATCOM 的补偿容量均为-180～180 Mvar ，TCSC的补偿度 rT为-0.2～0.7[15]。此外，采用牛顿拉夫逊法计算改进IEEE-14 节点输电网络的潮流。

4.2 算例求解

本文基于以上算例，分别使用PSO 算法和改进的SMPSO 算法对FACTS 设备进行优化配置。利用这2 种算法得到的最优解集分布情况如图4所示。

图4 利用两种算法得到的最优解集Fig.4 The optimal solution set of the two algorithms

由图4 可知，与传统PSO 算法相比，SMPSO算法搜索到的最优解集的补偿费用较低，并且具有更好的电压稳定性和更高的可用输电能力，解集的收敛性更优。

利用两种算法确定的FACTS 配置方案见表1。利用不同优化方案得到的优化结果见表2。

表1 利用两种算法确定的FACTS 配置方案Table 1 The optimization scheme of two algorithms

表2 不同优化算法配置方案效果对比Table 2 Comparison of different optimization schemes

由表2 可知：当风电系统满负荷时，对于利用PSO、 改进 SMPSO 算法确定的配置方案，ATC 分别为51.9，62.3 MW；相比于PSO 算法确定的优化配置方案，利用改进SMPSO 算法确定优化配置方案时，ATC 提高了 20.04%，补偿费用减少了19.83%；利用改进SMPSO 算法确定优化配置方案时，输电网的输电能力较大，输电系统的电压更加稳定，控制效果也更优。

图5为利用改进的 SMPSO 算法得到的Pareto 解集中粒子数的变化情况。

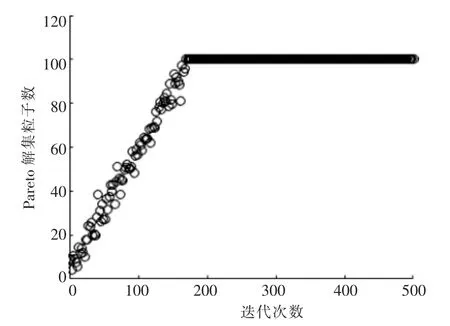
图5 利用改进的SMPSO 算法得到的Pareto 解集中粒子数的变化情况Fig.5 The number of particles in Pareto solution set obtained by improved SMPSO algorithm

由图5 可知，利用改进SMPSO 算法进行计算时，迭代174 次后，非劣解的数量逐渐趋于稳定，并且与要求的相互独立最优解集的个数相同。计算前期，随迭代次数的变化，Pareto 解集中粒子数出现小范围的持续波动，表明利用改进SMPSO 算法求解多目标问题时，能够实现持续的全局搜索。

此外，在种群数量为100，迭代次数为200 的条件下，利用改进SMPSO 算法和传统的PSO 算法进行寻优所需时间分别为186.362，198.457 s，表明利用改进SMPSO 算法进行寻优所需的时间较短。

5 结论

本文针对超高压大规模可再生能源外送系统的FACTS 规划需求，综合考虑多重约束，以提高电力系统的可用输电能力、 电压稳定性和运行经济性为目标，提出了一种基于自组织映射粒子群算法的FACTS 设备配置方法。分析结果表明，利用本文所提出的FACTS 设备配置方法，能够使电力系统的电压更加稳定，电力系统的可用输电能力也随之增强。