一类三次李氏卵圆

李湘江

(长沙理工大学工程训练中心,湖南 长沙 410114)

卵圆又称卵形线,是鸟类、禽类和爬行动物的卵,以及人和许多动物眼球中玻璃体的纵截面形状,是我们生活中常见的图形。人类对卵形线的直观认识由来已久,但对它的研究进展却较缓慢。有名的卵形线主要有:

(1) 笛卡尔卵形线[1]:A,B是平面内2个定点,m,n,b是3个固定正数,平面内满足m·PA+n·PB=b的点P的轨迹称为笛卡尔卵形线。若定义焦距2a,中点为原点,则笛卡尔卵形线方程为

(2) 卡西尼卵形线[2]:A,B是平面内2个定点,a,c是2个正数,AB=2c,平面内满足PA·PB=a2的点P的轨迹称为卡西尼卵形线,即到两定点距离的乘积为常数的点的轨迹,其方程为

(x2+y2)2-2c2(x2-y2)=a4-c4。

然而这些卵形线的参数范围限制较大,其应用受到很大制约。现今,由于科学及工程学的发展需要,特别是道路工程、建筑工程、医学眼科领域中卵形线的应用日益广泛,实际应用中卵形线大都是通过圆和椭圆的拼凑或组合形式即分段函数的形式给出[3-5],或者从生物学角度给出一类卵方程[6]。但至今对卵圆还没有一个明确的定义,仍然停留在圆和椭圆阶段[7-8]。

研究提出卵圆的一种精确定义,并且为了叙述方便,将新定义的卵圆取名为李氏卵圆。

1 定义

定义1平面曲线L,若满足如下条件:

①L有一条对称轴且是闭合的;

②L处处光滑;

③L上有唯一一对对称点,设为S、T,其到对称轴的距离最大;

④L与其对称轴有且仅有两个交点,设为P、Q,又PQ与ST交于一点,设为O,且OP>OQ;

⑤L为凸曲线,且不含直线段,

则称曲线L为李氏卵圆，称点O为李氏卵圆的卵心，分别称点P、Q为李氏卵圆的小端点和大端点，称点S、T为李氏卵圆的对称端点，称PQ的中点O′为李氏卵圆的轴心，过O′作对称轴的垂线交李氏卵圆于S′和T′，分别称线段OP、OQ、OS(或OT)、O′P(或O′Q)、O′S′(或O′T′)、OO′为李氏卵圆的长半径、短半径、对称半径、轴半径、次对称半径、偏心距，其长度分别记为a、b、c、e、g、h，并把正数a、b、c、e、g、h称为李氏卵圆的6个元素，而把a、b、c称为李氏卵圆的3个特征参数。

若取李氏卵圆的卵心为坐标系原点,小端点方向作为x轴的正向,则李氏卵圆在直角坐标系的示意图如图1所示。

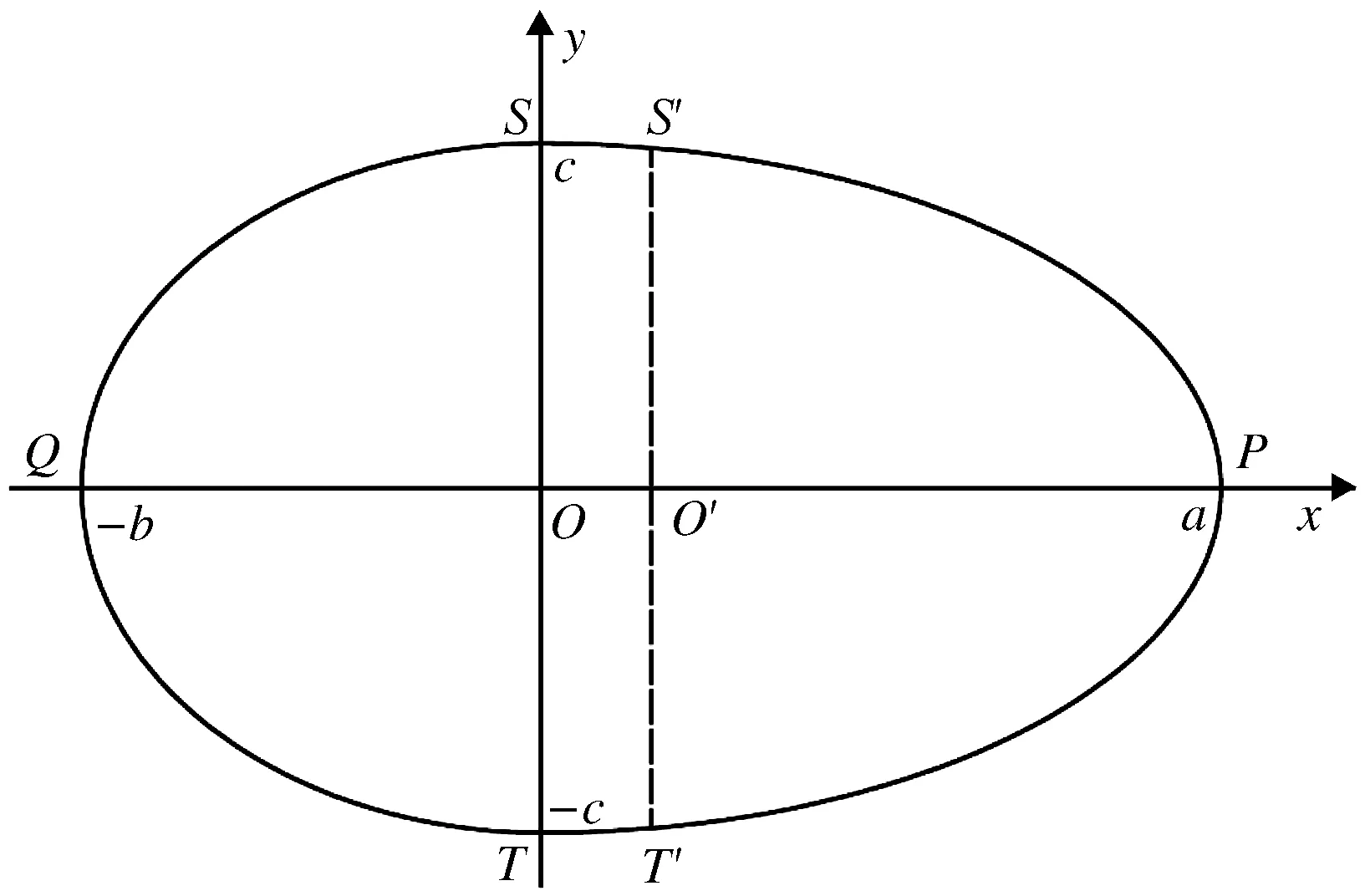
图1 李氏卵圆及其在直角坐标系示意图Fig.1 Li’s oval and its diagrammatic drawing on rectangular coordinate system

2 一类三次李氏卵圆方程

定理1设

a,b,c均>0,且a>b,

(1)

(2)

(3)

(a-b)xy2+c2x2+aby2-(a-b)c2x-

abc2=0,x∈[-b,a]

(4)

(5)

(6)

(a-b)x2y-abx2-c2y2-(a-b)c2y+

abc2=0,y∈[-a,b]

(7)

(8)

则方程(2)～方程(8)都是相互等价的,分别以a、b、c(a>b)为长、短、对称半径的李氏卵圆方程。

为了证明定理1,先证明如下引理。

引理1若方程(1)成立,则方程(2)～方程(8)互相等价。

证明由方程(2)经过恒等变形即可得到方程(3)和方程(4),故方程(2)～方程(4)互为等价。又将坐标轴绕原点逆时针旋转90°,则方程(2)～方程(4)分别变成方程(5)～方程(7),故方程(2)～方程(7)是互为等价的。

将方程(8)的第2式两边平方并化简,得

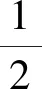
(9)

又将方程(8)的第2式代入-(a-b)y+ab,得

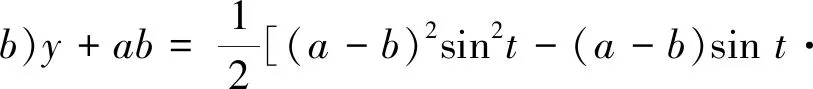
(10)

由方程(9)和方程(10)得

y2=[-(a-b)y+ab]sin2t⟹

(11)

又由方程(8)的第1式得

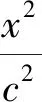
(12)

将方程(11)与方程(12)相加即得方程(5),故方程(8)是方程(5)的参数式方程,即方程(8)与方程(5)是等价的。故方程(2)～方程(8)是相互等价的。

引理2将参数方程(8)所确定的函数y(x)的一阶导数和二阶导数分别记为y′x(t)和y″x(t),则

y′x(t)=h(t)·u(t),

(13)

y″x(t)=w(t)·u(t)·v(t),

(14)

其中:

(15)

(16)

u(t)=(a-b)2sin2t+2ab-(a-b)sint·g(t),

(17)

v(t)=g2(t)+2(a-b)sintcos2t·g(t)+

(a-b)2sin2tcos2t,

(18)

(19)

证明由方程(8)得

y′x(t)=

上式化简得

[(a-b)2sin2t+2ab-

(20)

又

(21)

将方程(20)代入方程(21),并化简得

(22)

由式(20)及式(22)即得式(13)～式(19)。

引理3设式(1)成立,g(t)由式(19)所得，u(t)由式(17)所得，v(t)由式(18)所得，w(t)由式(16)所得，则

(ⅰ)

g(t)>0,t∈[0,2π]

(23)

(ⅱ)

u(t)>0,t∈[0,2π]

(24)

(ⅲ)

v(t)>0,t∈[0,2π]

(25)

(ⅳ)

w(t)<0,t∈(0,π)

(26)

w(t)>0,t∈(π,2π)。

(27)

证明(ⅰ)由式(19)和式(1)显然有

t∈[0,2π]

故式(23)成立。

(ⅱ)当t∈[π,2π]时,有sint≤0,则由式(17)、式(23)和式(1),得

u(t)≥2ab>0,t∈[π,2π]。

(28)

当t∈(0,π)时,有sint>0,则由式(17)及式(23),得

u(t)>0⟺(a-b)2sin2t+2ab>(a-b)sint·

g(t)⟺[(a-b)2sin2t+2ab]2>

(a-b)2sin2t·g2(t)⟺(a-b)4sin4t+

4ab(a-b)2sin2t+4a2b2-

(a-b)2sin2t[(a-b)2sin2t+4ab]>0⟺

4a2b2>0。

由式(1)知,上式的最后不等式显然成立,于是得

u(t)>0,t∈(0,π)

(29)

又

u(0)=2ab>0,

(30)

由式(28)～(30)即知式(24)成立。

(ⅲ)由式(18)知v(t)可视为g(t)的二次函数,且二次项系数=1>0,其判别式

Δ=4(a-b)2sin2tcos4t-4(a-b)2sin2tcos2t=

4(a-b)2sin2tcos2t(cos2t-1)=

-4(a-b)2sin4tcos2t,

由上式及式(1)知,当

时,有Δ<0,从而v(t)>0。

v(2π)=g2(2π)>0。

综上即知式(25)成立。

(ⅳ) 当t∈(0,π)时,有 sint>0;当t∈(π,2π)时,有 sint<0,于是由式(16)、式(23)及c>0得

w(t)<0,t∈(0,π),w(t)>0,t∈(π,2π)。

故式(26)和式(27)成立。

引理4设式(1)成立,y″x(t)是由参数式方程(8)所确定的函数y(x)的二阶导数,则

y″x(t)<0,t∈(0,π)

(31)

y″x(t)>0,t∈(π,2π)。

(32)

证明由引理2与引理3,即由式(14)、式(24)和式(26)得式(31),由式(14)、式(24)和式(27)得式(32)。

定理1的证明首先证明方程(3)的图形曲线L满足定义1的条件①～④。

为此,先考察式(3)的带“+”号的函数

(33)

求出函数(33)的导数,并化简,得

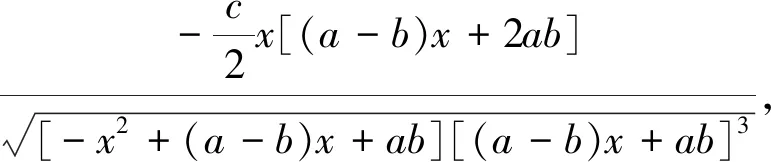
x∈[-b,a]

(34)

由式(3)知,其图形曲线L显然关于x轴对称且是闭合的,故L满足定义1的条件①。

由式(34)知,式(33)的函数y(x)的导数y′(x)在区间(-b,a)内处处有限存在,在端点x=-b,x=a处均为,故知函数(33)的曲线即L的上半部在x∈[-b,a]上处处存在切线,从而是处处光滑的。由对称性知,整个曲线L在x∈[-b,a]上也是处处光滑的,故L满足定义1的条件②。

又由式(34),令y′(0)=0,得式(33)的函数y(x)在x∈[-b,a]上仅有一个稳定点x=0,且由式(34)知

y′(x)>0,x∈(-b,0)

y′(x)<0,x∈(0,a)。

故x=0是函数(33)在区间x∈[-b,a]的唯一极大值点[9],也是最大值点,且由函数(33)知最大值y(0)=c,由对称性知,L上存在唯一一对对称点S(0,c)、T(0,-c),到对称轴x轴的距离最大,且最大距离为c。所以L满足定义1的条件③。

在方程(3)中令y=0,得x=a及x=-b,故L与其对称轴x轴有且仅有2个交点P(a,0)、Q(-b,0),又PQ与ST相交于坐标系原点O(0,0),且OP=a>b=OQ,故L满足定义1的条件④。

由引理1知,方程(2)～方程(8)均为相互等价的,故方程(2)～方程(8)的图形曲线L均满足定义1的条件①～④。

其次证明方程(8)的图形曲线L是凸的,且不含直线段。由引理4,即式(31)知,曲线L在t∈[0,π]上即L的上半部是上凸的且不含直线段[9],由式(32)知,曲线L的下半部是下凸的且不含直线段。故整个曲线L是凸的且不含直线段,即L满足定义1的条件⑤。

综上,即知方程(8)的图形曲线L确实是满足定义1的李氏卵圆。方程(8)为李氏卵圆方程。再由引理1即知定理1成立。

由定理1,给出如下定义。

定义2设方程(1)成立,则:

① 称方程(2)为标准李氏卵圆方程;

② 称方程(2)和方程(5)为对称式李氏卵圆方程;

③ 称方程(3)和方程(6)为显函数式李氏卵圆方程;

④ 称方程(4)和方程(7)为一般式李氏卵圆方程;

⑤ 称方程(8)为参数式李氏卵圆方程;

⑥ 称方程(2)～方程(4)为横向李氏卵圆方程;

⑦ 称方程(5)～方程(8)为纵向李氏卵圆方程。

注1在方程(2)中,令b=a,则方程(2)变成

上式显然为一椭圆方程。故三次李氏卵圆方程(2)～方程(8)是椭圆的推广。

定理2设

A,B,C>0,

(35)

则

Axy2+Bx2+Cy2-ABx-BC=0

(36)

为李氏卵圆方程,且卵圆的长、短、对称半径为

(37)

证明考察如下的三次方程:

Axy2+Bx2+Cy2-Dx-E=0。

(38)

比较方程(38)与方程(4)的系数,得

A=a-b,

(39)

B=c2,

(40)

C=ab,

(41)

D=(a-b)c2,

(42)

E=abc2。

(43)

由式(39)、式(40)和式(42)得

D=AB。

(44)

由式(40)、式(41)和式(43)得

E=BC。

(45)

将式(44)和式(45)代入式(38)即得式(36)。

由式(39)～式(41)联立并反解即得式(37)。

由式(35)和式(37)得a、b、c均>0且a>b,即式(1)成立,从而由定理1知,式(4)为李氏卵圆方程,故式(38)为李氏卵圆方程,从而式(36)为李氏卵圆方程,且式(37)成立。

3 三次李氏卵圆的切线方程和法线方程

定理3设(x0,y0)是三次李氏卵圆(2)上的一点,则三次李氏卵圆(2)过点(x0,y0)处的切线方程和法线方程分别为

(46)

(47)

证明由方程(2),令

则

故

(48)

又过点(x0,y0)且斜率为y′x(x0,y0)的直线为

y-y0=y′x(x0,y0)(x-x0)。

(49)

将式(48)代入式(49)即知式(46)成立。同理可知式(47)成立。

4 三次李氏卵圆旋转卵球体的体积

定理4设三次李氏卵圆(3)绕x轴旋转而成的卵球体的体积为V,则

(50)

证明由方程(3)得

(51)

由旋转体的体积公式[9]及式(51)得

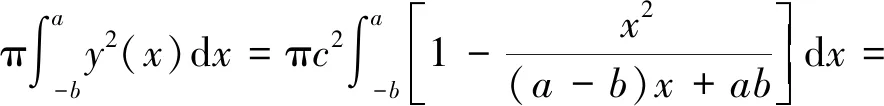
故式(50)成立。

注2令b→a,用洛必达法则[9],由式(50),可得

所得结果正是旋转椭球体的体积公式。这也佐证了式(50)的正确性。

5 实例与仿真验证

5.1 实例

以下给出一个具体的三次李氏卵圆方程,比如取a=5、b=4、c=3,代入式(2) 得李氏卵圆方程

(52)

用计算机绘制的图形如图2所示。

5.2 仿真验证

为了验证研究所建三次李氏卵圆方程图形与真实卵形对比效果,用计算机编写了一个仿真绘图程序。取一张鸡蛋照片作为绘图程序界面上绘图区的背景。通过像素分析和计算,获得图片中鸡蛋图像横向最大像素为386,纵向最大像素为294,在鸡蛋图片横向和纵向最大像素处画2条直线作为x轴、y轴,x轴与y轴的交点即为鸡蛋的卵心,并将卵心位置设定为绘图区的原点。程序界面如图3所示。

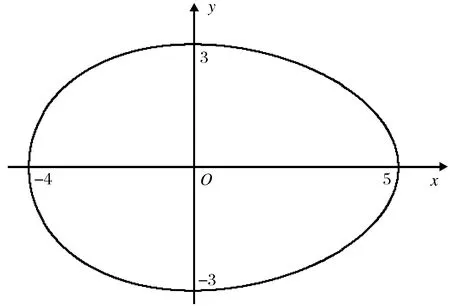
图2 方程(52)图形Fig.2 Equation (52) graph

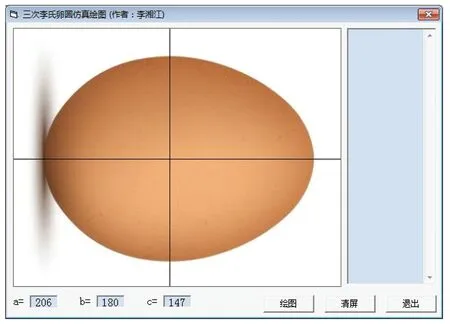
图3 绘图程序界面Fig.3 Drawing program interface

按卵圆方程的需求量取鸡蛋以像素为单位的长、短、对称半径3个参数值,得出a=206、b=180、c=147。则由式(3)得其李氏卵圆方程

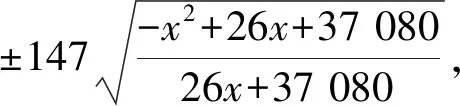
x∈[-180,206]。

(53)

绘图程序使用方程(53)进行计算并通过描点法绘制图形。程序界面右侧文本框中显示方程取点的计算值。绘图程序运行结果如图4所示。

图4中鸡蛋外轮廓的黑色图线是绘图程序根据李氏卵圆方程(53)绘制的卵圆图形,黑色卵圆图线与图片中鸡蛋外轮廓高度吻合。

图4 绘图程序运行结果Fig.4 Running results of the drawing program

6 结语

众所周知,圆只有一个参数(半径r),椭圆有2个参数(半长轴p,半短轴q),而卵圆与它们的主要区别在于它有3个参数(长半径a,短半径b,对称半径c),研究所提出的李氏卵圆的定义正是抓住了卵圆的这种本质特征。当然符合所述定义的李氏卵圆方程不是唯一的,其他满足李氏卵圆定义的方程有待进一步研究。

二次方程已经被研究得非常彻底,凡二次方程均为圆锥曲线或直线或空集[10],故从二次方程中不可能得到卵圆方程。历史上一些有名的卵形线,如卡西尼卵形只有2个参数,笛卡尔卵形线虽然有3个参数,但参数范围限制较大,其应用受到很大制约。到目前为止,所发现的卵形线方程均不低于4次,而研究证得的这类三参数李氏卵圆方程仅为3次,比其他所有卵形线方程的次数均低,且更简单,只要三参数a、b、c均为正且a>b即可。利用它可以快速绘制出精确的卵圆图形,同时也给卵圆及其应用研究提供了理论基础。