土质滑坡滑前三维地形恢复研究

王振宇,张常亮,周潇朗,魏岩朔

(长安大学地质工程与测绘学院,陕西 西安 710054)

滑坡作为自然界中一种常见的地质灾害,对人类的生命财产安全危害极大,因此要寻找有效的方法对滑坡灾害进行防治。

要对滑坡进行有效防治,就需要对其形成机理进行分析,而研究其形成机理则需要从滑坡未破坏前到破坏后的整个过程开展滑坡的应力应变发展变化分析,这就需要获得其未滑前的原始地形。通常原始地形的恢复都是借助当前滑坡的形态,根据滑坡周围原始地形推测出滑坡原始地形,如李萍等[1]认为滑坡形成后其周界没有滑动,可将等高程的周界点连接,近似地认为是原地形,根据滑坡周界和滑坡主轴线上的测量点计算其主滑断面上的原地形坐标和高程,获得滑坡主轴线上的原始地形断面。该方法往往仅能获得滑坡的主滑二维断面形态,且因其仅考虑周围地形的影响,对待具有简单原始坡形的滑坡可以近似恢复二维地形,对复杂边坡形成的滑坡则会产生较大误差。随着技术的发展,越来越多的研究人员开始利用INSAR技术对区域性的滑坡和单点滑坡滑前滑后的形态进行监测,然后利用GIS手段对滑前滑后的地形进行分析,建立滑坡各阶段的三维地形模型,如康亚等[2]利用INSAR在乌东德库区成功进行了大范围的滑坡探测;何朝阳等[3]运用INSAR技术进行了潜在滑坡早起变形体的识别;朱文峰等[4]利用INSAR识别与监测黑方台黄土滑坡,证明此技术不仅方便可靠,而且精确度高;张文馨等[5]利用INSAR技术对矿区地面沉降进行监测,进而得到矿区地面沉降信息;Davis等[6]基于GIS和可视化技术对具有空间性不确定的滑坡进行了可视化建模;Xie等[7]也在GIS支持下建立了滑坡三维稳定分析模型,并运用蒙特卡罗法搜索最危险滑动面;乔建平等[8]结合人工智能技术和GIS实现了三维可视化滑坡危险度的判别等;王旭春等[9]利用GIS可视化技术建立了滑坡三维分析模型,进而确定滑坡主滑动方向。这些研究的开展对将滑坡的形成机制研究推展到三维状态提供了很好的方法,但也可以看出,此种方法需要长期持续对滑坡开展监测,以获得每个阶段的地形数据,过程复杂,造价昂贵,且对于未处于监测区域的滑坡无法获得其原始地形数据,这也限制了该方法的应用范围。

为此,以山西省吕梁市针南川河滑坡为研究对象,通过仿真技术对现有滑坡坡形和周围地形的三维地形数据进行模拟,获得当前滑坡的三维坡形,然后参考滑坡体积量和滑坡周围原始稳定地形,建立多种坡形下的滑前原始三维地形,结合各地层力学参数,利用运动模型[10]对各种坡形下的滑坡进行运动变化分析,获得滑坡破坏后的三维分布形态。通过与当前滑坡三维形态的对比,选择出最符合当前滑坡运动学特征和分布特征的坡形作为滑坡的原始三维地形。最后利用该三维地形建立其对应的三维数值模型,分析其应力应变特征和变形特征,验证该模型的准确性。通过以上方法,研究尝试建立针对无法获得原始地形数据土质滑坡的原始三维地形恢复方法。

1 研究案例

南川河滑坡位于山西省吕梁市南川河南岸,滑坡前缘为南川河一级阶地,后壁到前缘呈波浪状起伏,长度220 m,最大宽度635 m,滑体厚10～30 m,滑坡体积约85万m3,滑体覆盖面积8.7万m2,最大水平滑动距离30 m。未滑动之前斜坡高121.0 m,坡角45.8°。

滑坡发生后,现场实测滑坡断面,根据邻近边坡地形恢复滑前的断面,滑坡剖面如图1所示。滑坡地层顶部为60 m厚黄土层,其中Q3厚12 m,Q2厚45 m,Q1厚11 m;中部为厚3 m左右的冲洪积物,底部为砂泥岩互层的基岩,未见地下水出露。通过试验和规范得出滑坡区岩土物理性质数值,如表1所列。

图1 南川河滑坡剖面Fig.1 Landslide profile of Nanchuan River

表1 滑坡区岩土物理性质统计Table 1 Statistics on the physical properties of soil in the landslide area

2 滑坡当前三维地形建立

通过实际勘察测量,获得滑坡当前地形高程数据,然后将地形高程数据坐标转化为建模所需的坐标,以一条边为准,其他点数据转化为相对点,然后模拟符合该地形统计特征的随机过程,形成一定数量用来表示地形框架的特征点,结合滑坡模拟所用模拟参数(见表2),再进行一定的数据处理,形成用规则网格表示的地形整体框架,再利用分形技术中的中点位移的方法产生地形的局部细节,生成与真实地形相似的仿真地形,获得当前滑坡的三维坡形(见图2)。

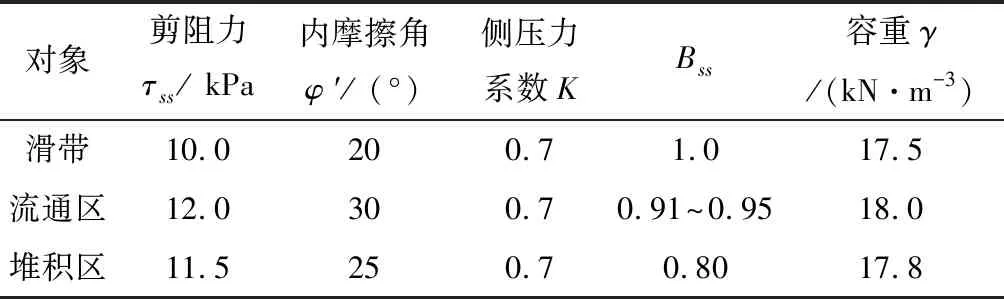
表2 用于滑坡模拟的数据Table 2 Data for landslide simulation

图2 滑坡当前三维地形Fig.2 Three-dimensional terrain of landslide

3 滑坡滑前三维地形推测

黄土滑坡的地貌特征比较明显,后缘陡壁直立,周界突出,呈圈椅状,前缘剪出口多在基岩顶面,可以认为滑坡前的原始边坡是极限状态,因此认为滑坡后,滑坡后缘及周围边界地形没有变化,根据滑坡方量与滑坡周围高程数据还原原始地形。而自然界中斜坡一般按照剖面曲率将坡面形态分为3类(见图3),曲率<-0.5时为凹形坡;曲率在-0.5～0.5时归为直线形坡;曲率>0.5时为凸形坡。滑坡后缘及边界情况已知,控制滑坡方量即得到3种不同坡形的滑坡滑前三维地形(见图4～图6)。

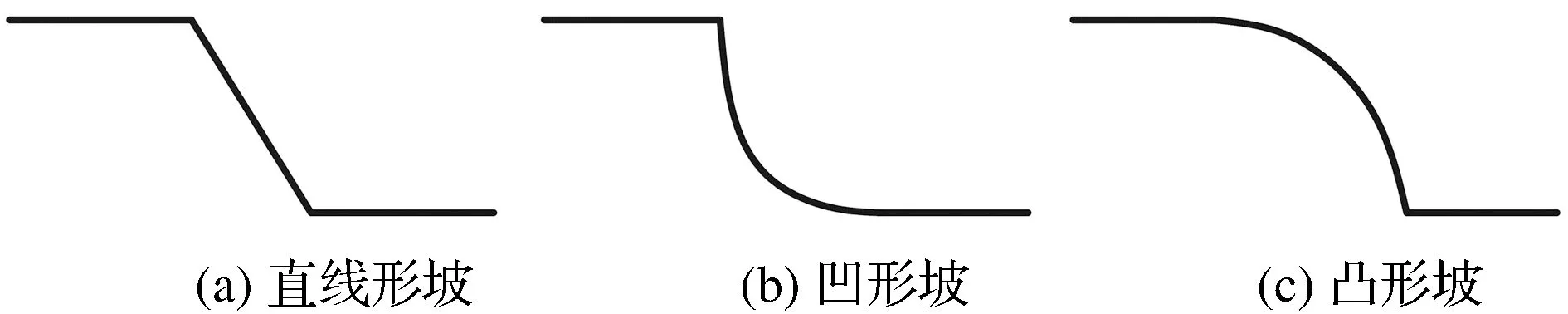
图3 斜坡坡型示意图Fig.3 Slope diagram

图4 滑坡滑前凸坡三维地形Fig.4 Three-dimensional terrain of convex slope before landslide

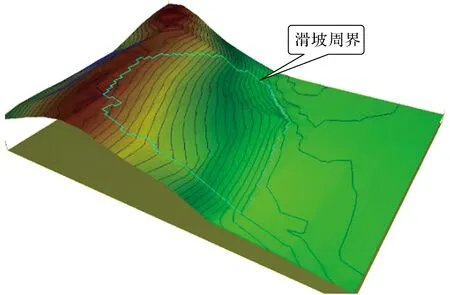
图5 滑坡滑前凹坡三维地形Fig.5 Three-dimensional terrain of concave slope before landslide

4 推测不同坡形下的运动学分析

4.1 Sassa K模型运动分析基本原理

根据仿真基本原理(见图7),滑坡体是由无数个假想的垂直柱体构成。假设滑坡体的总体积不发生变化,只有各柱体高程发生变化,即各高程增加量为0,以此来模拟滑坡运动。

图6 滑坡滑前直坡三维地形Fig.6 Three-dimensional terrain of constant slope before landslide

图7 仿真基本原理Fig.7 Basic principle of simulation

滑坡体双层结构如图8所示,假设滑动质量由2层组成:第1层是相对连贯的滑动碎屑层,第2层是较薄的滑动区。上部碎屑层的厚度在滑坡运动过程中会发生变化。滑坡运动过程中,滑坡体厚度变薄,最终形成沉积体是滑坡的普遍现象。根据该模型,当作用于滑动区的法向应力减小时,其表观摩擦系数将相应增加。如果滑坡运动中的抗剪力是恒定的话,将导致滑坡运动自动停止。滑坡运动中,滑体抗剪力、表观摩擦系数及其他主要影响因素关系为

τss(h,Bss)=τss+(σ(h)tanφ′r-τss)(1-Bss),

(1)

σ(h)=ρghcos2θ,

(2)

(3)

其中:τss为稳定状态下滑动区土体的抗剪力;φ′r为有效残余摩擦角;Bss为超孔隙压力累积的可能性;τss(h,Bss)为当滑动质量的厚度在h位置,超孔隙压力累积的可能性是Bss;φa为滑动区土壤的表观摩擦系数。

图8 滑坡体双层结构Fig.8 Double layer structure diagram of landslide

边坡破坏后,随着滑坡的加速,抗剪强度将下降到稳定状态。在滑坡体运动过程中,正应力会减小,导致表观摩擦角增大,从而导致滑坡运动停止。

4.2 不同坡形运动结果分析

南川河滑坡凸坡三维滑动过程模拟如图9所示。假设滑前的滑坡地形如图9(a)所示,原地形较周围地形较高,形成一凸坡,滑坡的左右两翼较周围地形落差较大,等高线密集。对比滑坡见稳定后的堆积形态[见图9(b)]和实际地形(见图2)的地面形态,发现模拟凸坡的滑距较实际大,滑动范围也比实际地形广,特别是滑坡前缘左侧滑动范围较实际地形大了好多,滑动后地面形态有所差别,模拟凸坡中部由于滑前坡体较高,在滑动稳定后依然有突起,而实际地面形态呈平缓下降,由于右侧较左侧陡,所以滑坡滑动方向稍向左偏,导致滑坡稳定后的左侧地形与实际地形有较大误差。因此,在降低此凸坡模拟数据高程数据基础上又做了南川河滑坡凹坡三维滑动过程模拟。

图9 南川河滑坡凸坡三维滑动过程模拟Fig.9 Simulation of the three-dimensional sliding process of landslide of convex slope of Nanchuan River

南川河滑坡凹坡三维滑动过程模拟如图10所示。相比与之前的凸坡高程,凹坡相对降低了40 m,整体坡形较平缓,等高线较稀疏。对比滑坡凹坡稳定后的堆积形态[见图10(b)]和实际地形(见图2)的地面形态,发现模拟凹坡的滑距比实际小很多,滑动范围也比实际地形窄,模拟的凹坡只有对比滑坡直坡稳定后的堆积形态[见图11(b)]和实际地形(见图2)的地面形态,发现二者滑距基本一致,滑动范围基本相同,滑动后地面的形态基本相似。

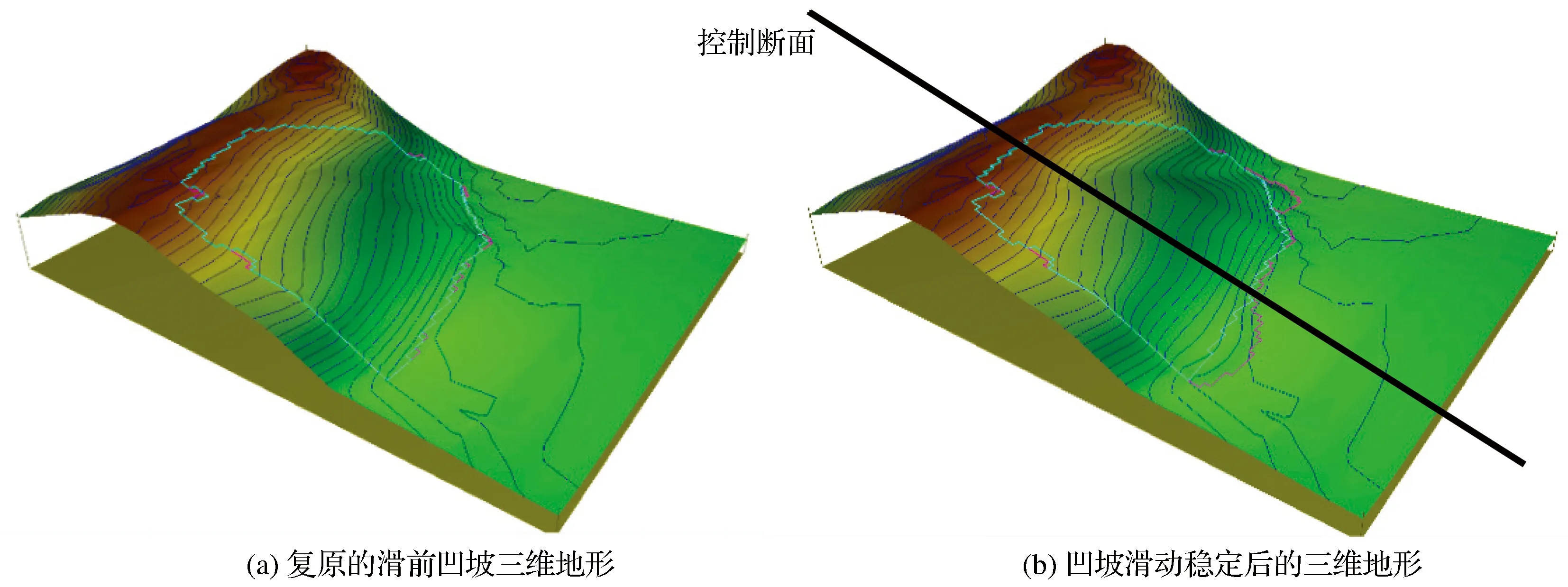
图10 南川河滑坡凹坡三维滑动过程模拟Fig.10 Simulation of the three-dimensional sliding process of landslide of concave slope of Nanchuan River

滑坡前缘的左右两侧发生少量滑动,滑坡前缘中部基本无滑动,滑动后地面的形态也有所区别,虽然滑动方向基本一致,但由于滑坡前缘基本无滑动,滑坡中部坡形基本无变化,并未出现实际坡体中部的低陷,只滑动方向主轴两侧出现了不太明显的斜沟。此后,又在这二者之间多次结合周围地形调整高程,得到了在滑动稳定后与实际地形较符合的南川河滑坡三维滑动过程模拟,如图11所示。

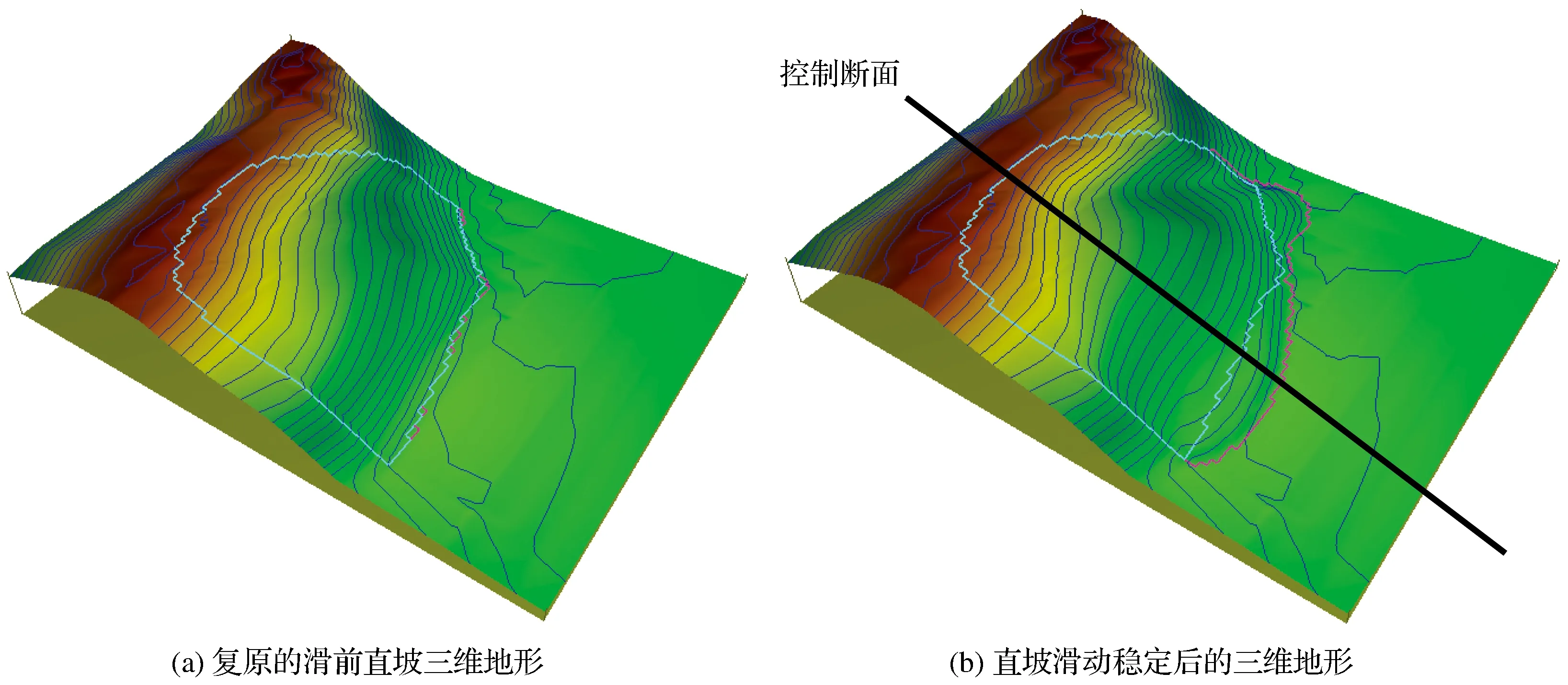
图11 南川河滑坡直坡三维滑动过程模拟Fig.11 Simulation of the three-dimensional sliding process of landslide of constant slope of Nanchuan River

此外,通过导出各状态滑坡稳定后的实际地形高程数据,选取控制断面高程数据,得到不同坡形滑动稳定后同一剖面剖面图(见图12)。从图12中可以看出,凸坡与凹坡在滑动稳定后的地形与实际地形存在偏差,而直坡滑动稳定后与实际地形基本相似,误差在允许范围内。

图12 不同坡形滑动稳定后同一剖面对比Fig.12 Same profile after stabilization of different slope sliding

5 最优滑前恢复地形的验证分析

结合模拟所得南川河滑坡滑前原始地形,运用GTS NX建立三维模型,首先导入直坡滑前的高程点,生成面然后用箱体切割出坡体,使用Mohr-Coulomb材料模型,其物理力学参数见表1,然后以10为尺寸控制播种,进一步进行混合网格划分,划分为131 918个节点,155 120个单元,以Morgenstern-Pric极限平衡法为稳定性判别依据。将地面定义为自由位移边界,其余5个面为固定位移边界,建立南川河滑坡三维模型(见图13),通过查询资料发现,其所处地方构造活动并不强,故将x轴方向的侧压力系数K0x和y轴方向的侧压力系数K0y都设为1.0,建立初始应力场,进行计算分析。研究分析其稳定系数为1.103 8,因此该滑坡处于极限平衡状态,并得到了滑坡最大剪应力图(见图14)和滑坡剪切应变图(见图15),根据所得到应力应变分布云图进一步分析其划破破坏范围。

图13 南川河滑坡三维模型Fig.13 Three-dimensional model of the Nanchuan River landslide

从图14和图15可以看出,滑坡的最大剪应力分布自上往下逐渐增大,这与其应力大小成正比,越往下越大。而且在图14中可以看出,滑坡左缘出现了剪力突然变大的现象,这表明坡体在此处出现不稳定,对应图15可知,此处刚好是剪切应变集中区,即滑坡破坏的大致范围,滑坡左前缘首先出现剪应变集中现象,失稳下滑进而导致滑坡后缘整体出现滑动,这与Sassa K所做的模拟结果基本相似,因此证明复原的滑前三维地形基本符合,也可以更加直观的观察其破坏的范围。

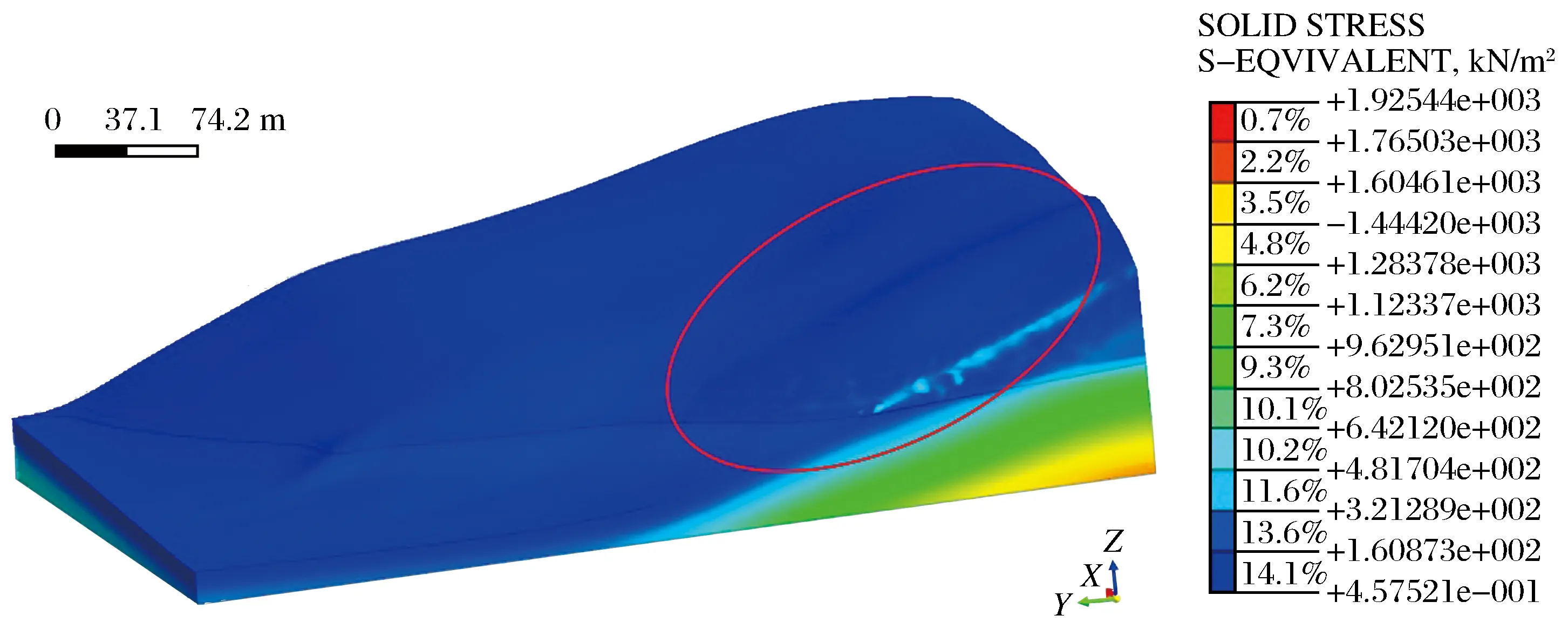
图14 滑坡最大剪应力Fig.14 Maximum shearing stress of landslide

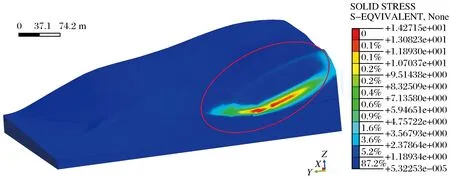
图15 滑坡剪切应变Fig.15 Shearing strain of landslide

6 结论

对滑坡进行有效防治,就需要从滑坡未破坏前到破坏后的整个过程开展滑坡的应力应变发展变化分析,这就需要获得其未滑前的原始地形。以山西省吕梁市南川河滑坡为研究对象,对其进行了三维原始地形恢复,得出以下结论:

(1) 利用仿真原理结合滑坡岩土体物理力学参数与地形高程,建立滑坡当前地形,可以为恢复滑坡滑前地形打好基础。

(2) 滑坡后,滑坡后缘及周围边界地形没有变化,根据滑坡方量与滑坡周围高程数据还原原始地形,建立不同坡形来运用Sassa K模型模拟滑坡运动过程,通过滑距、滑动范围、滑动后地面的形态等来确认相对合理的滑前地形。

(3) 运用数值模拟,结合找出的滑前三维地形,滑坡体基本物理力学参数,分析其应力应变特征和变形特征,验证该模型的准确性。通过这一整套的流程,尝试建立针对无法获得原始地形数据土质滑坡的原始三维地形恢复方法。

同时,研究内容在以下2个方面还有待改进:(1)虽然通过高程数据与岩土参数还原了三维原始地形,但滑坡真正的发生过程,其内部构成物质大小、形态、力学性质都会影响滑坡的发展,要完全模拟真实的地形在理论和实践上都存在很大的困难;(2)对于原始地形虽然有一定进展,但整个模拟过程数据分析量庞大,而且分析的工况比较有限,需要加以改进。