非线性本构关系下两端固定梁的弯曲变形

曲昭霞,赵永刚,秦慧峰

(兰州理工大学理学院,甘肃 兰州 730050)

经典力学认为在构件的变形过程中材料的弹性系数是不变的,即在弹性范围内应力-应变本构关系是线性关系。实际上,材料的本构关系并非完全是线性的。早在20世纪60年代末,研究者就注意到某些材料具有明显的非线性本构关系,如陶瓷、石墨、混凝土、多孔材料和一些有机材料、复合材料、软材料等。相关的理论和实验研究表明材料的弹性系数在构件的变形过程中是变化的,这一变化在主应力正负号发生变化时最为明显,研究者把受拉和受压阶段的弹性系数分别进行了线性化处理,认为在受拉和受压阶段弹性系数分别为常数,由此建立了拉压不同弹性模量理论,也称为双模量理论。苏联学者Ambartsumyan在1982年完成了第一本关于该理论的著作《不同模量弹性理论》[1]。近年来,国内外众多学者针对弹性构件进行了大量的力学研究[2-10]。

考虑连续变化的本构关系,认为材料的弹性系数是应变的函数,对横向均布载荷作用下的梁的非线性弯曲问题展开研究。通过数值结果讨论了本构关系的非线性参数对梁弯曲变形的影响。

1 基本方程

我们研究一具有非线性应力-应变本构关系的矩形截面梁的弹性弯曲问题。梁的长度为l,横截面高度为h,宽度为b,梁上承受铅垂方向分布载荷q的作用。基于几何中面建立直角坐标系Oxyz(见图1),x轴为梁的轴线,y轴和z轴分别选取了矩形横截面的水平和铅垂对称轴。

图1 梁的结构和坐标系示意图Fig.1 Diagram of beam structure and coordinate

1.1 几何关系

梁在发生弯曲变形时,几何中面上的轴向应变ε0为

(1)

其中:u、w分别表示中面上的轴向和铅垂位移。若乘子p=0,式(1)即为梁的小挠度弯曲的几何关系,而乘子p=1时为大挠度弯曲情况。

对于非中面层上的任一点的变形情况,其应变ε为

(2)

1.2 物理方程

在研究梁的弯曲变形时,假设材料的弹性模量E是应变的函数,即E=E(ε)。作为特例,研究时选取了弹性模量是应变的线性函数,即

E(ε)=E0+E1ε,

(3)

其中:E0是初始变形时材料的弹性模量;E1是材料弹性模量随应变线性变化的参数,该参数体现了本构关系的非线性特性。

梁弯曲变形时,横截面上的正应力为

σ=E(ε)·ε=(E0+E1ε)ε=E0(ε+Erε2),

(4)

(5)

1.3 静力学关系

当梁上承受如图1所示的横向分布载荷时,研究微段的平衡,得到内力平衡方程为

(6)

(7)

2 对基本方程的无量纲化

为了计算方便,引入下列无量纲参数:

(8)

无量内力的表达式为

(9)

无量纲控制方程为

(10)

位移形式的无量纲边界条件为

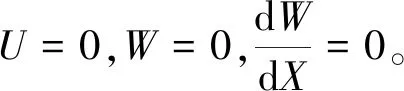
3 数值求解及结果分析

图2给出了长细比δ=0.08,本构非线性参数Er不同时,两端固定梁小挠度问题(p=0)的中点挠度W(0.5)随载荷Q变化的平衡路径。从图2中不同Er值的路径曲线可以发现,Er=0时,中点挠度随载荷Q的增加而线性增加；Er≠0时,挠度-载荷关系不再是线性的,且在Er取正值和负值时,分布在Er=0直线的两侧。当Er>0时,中点挠度变小,反映了梁的抗弯曲变形能力增加了;而Er<0时,曲线在上方,则体现了梁的抗弯曲变形能力下降了,呈软弹簧效应。

图3给出了Q=100,δ=0.08,本构非线性参数Er不同时,两端固定梁的小挠度弯曲构形和中性层的位置。其中横坐标x为梁轴线上的坐标点,纵坐标为弯曲过程中的位移构型和中性层位置。从图3可以看出,梁的弯曲变形随着Er的增大而减小,弯曲平衡构形的拐点截面上无弯矩,不存在弯曲中性层,从弯曲构形的拐点处,把梁分成3部分,每一部分中性层位置都有正负间连续变化。由于几何中面轴向变形的约束,使得Er≠0时横截面上产生轴向力,内力弯矩引起中性层偏离几何中面,轴力对中性层位置也有影响。因此,Z0=0的截面上这2种影响相互抵消。

图2 两端固定梁小挠度问题的平衡路径Fig.2 Equilibrium path of the small deflection problem of built-in beams at both ends

图3 两端固定梁小挠度问题的平衡构形和中性层位置Fig.3 Equilibrium configuration and neutral layer position in the small deflection problem of built-in beams at both ends

图4给出了长细比δ=0.08,本构非线性参数Er不同时,两端固定梁大挠度问题(p=1)的中点挠度W(0.5)随载荷Q变化的平衡路径。

图4 两端固定梁大挠度问题的平衡路径Fig.4 Equilibrium path of the large deflection problem of built-in beams at both ends

从图4可以看出,在Er=0时,挠度-载荷的曲线关系是非线性的,这是几何关系非线性问题的特性。在Er≠0时同样有平衡路径分布在Er=0时的两侧,但Er<0时不再呈现软弹簧效应。在W(0.5)较小时,大挠度问题解与小挠度问题解就有了明显的差别。Q=75,Q=125时小挠度问题与大挠度问题解的比较见表1。由表1可以看出,Er>0时小挠度问题和大挠度问题的解相对误差更大,于是小挠度解的适用范围就更小。

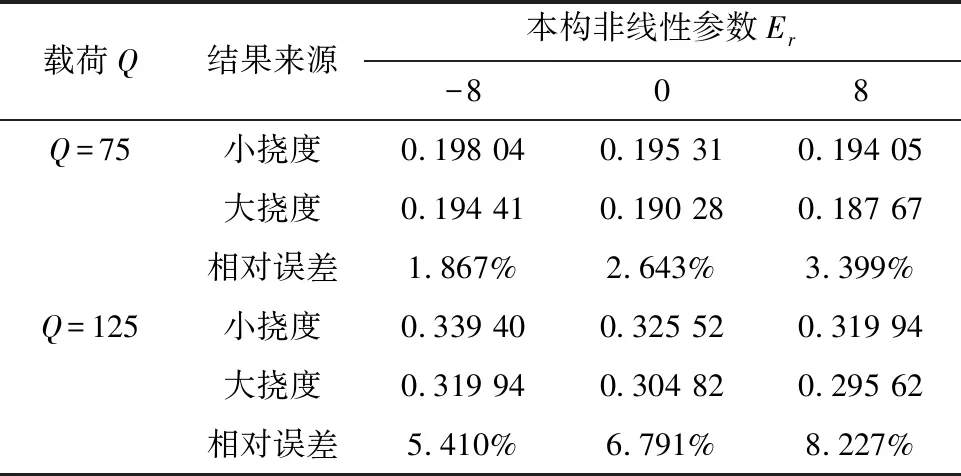
表1 小挠度问题解和大挠度问题解的比较

图5给出了在Q=100,δ=0.08,本构非线性参数Er不同时,两端固定梁的大挠度中性层位置。其中横坐标x为梁轴线上的坐标点,纵坐标为弯曲过程中中性层的位置。

图5 两端固定梁大挠度问题的中性层位置Fig.5 Neutral layer position in the large deflection problem of built-in beam at both ends

同图3(b)比较可以看出,由于几何非线性的影响,中性层位置不会因为Er的正负变化而反向,这说明大挠度问题中,轴向拉力对弯曲变形的影响比较大。结合表1的数值结果可以看出:对于非线性本构关系材料的梁的弯曲问题,即使在变形较小时也应采用大挠度方程求解。

4 结论

基于非线性本构关系研究了两端固定梁在横向均布载荷作用下的弯曲问题。假设材料弹性模量是应变的线性函数,运用数值方法求解了该支承条件下的小挠度弯曲和大挠度弯曲的数值结果。结果表明:

(1) 本构关系的非线性参数对梁的弯曲变形有影响。弯曲变形与Er的符号有关且随着Er的增大而减小。

(2) 由于几何中面轴向变形的约束,使得Er≠0时横截面上产生轴向力,梁的中性层位置发生变化,且横截面中性层随着Er的变化而变化。

(3) 非线性本构关系下的弯曲问题,应采用大挠度问题的方程求解。