灰色BP神经网络组合模型在大坝沉降监测中的应用
2020-02-24冯钱桢
冯钱桢,黄 腾
(河海大学地球科学与工程学院, 江苏 南京 211100)
我国是一个水利大国,拥有世界上最多的大坝数量。历史上灾难性的溃坝多次发生,每次都造成了巨大的人员伤亡和财产损失。所以对大坝实施准确、实时的沉降监测非常重要。近些年一些大坝设置了固定自动监测点,实现了自动化监测,实现实时监测和沉降分析、预报。而对于未设置固定自动监测点的大坝,则需要对大坝进行定期的沉降监测[1-2]。
影响大坝沉降的因素有很多,例如建筑物材料、地质条件、地下密封性等,所以对沉降预测模型的选择显得十分重要。国内外学者对此做了很多研究。郑旭东等[3]利用熵权法并联组合模型对大坝监测数据进行处理,拟合出变化趋势,从而得到预测结果;谢朋朋等[4]提出了一种变权组合预测模型对大坝沉降数据进行预测,预测精度高于单一模型精度,为大坝沉降变形预测提供了一种有益的参考;苏观南等[5]将卡尔曼滤波灰色模型应用在大坝变形监测中,预测精度较好,但是长期预测会有发散性问题;李萌等[6]将通过灰色模型改进的分形几何预测模型应用于大坝变形监测中,其预测结果有更好的稳定性和抗干扰性。
上述文献中提到灰色模型主要应用于数据量少、随机变化、不完整的数据序列,所以对影响因素繁多且不确定的大坝沉降预测有着独特的优势,但是如果数据序列是非线性的,灰色模型的预测结果则不尽如人意,并且不能用于长期预测、不能控制误差,而BP神经网络模型通过不断训练改变网络神经元的权值,能够对灰色系统的误差进行补偿,从而能处理非线性的数据序列[7-8]。研究以某大坝沉降监测数据为例,运用灰色BP神经网络组合模型对其沉降进行预测。
1 灰色GM(1,1)模型
1.1 模型建立
灰色系统理论是我国学者邓聚龙教授于1982年3月提出来的,灰色系统理论作为一种数学模型,主要用来解决信息不完备的小样本数据问题[9],其中最常用的就是GM(1,1)模型,其建模过程如下:
(1) 设一组原始数据为X(0)=(x(0)(1),x(0)(2),…,x(0)(n)),n为数据个数。对X(0)做一次累加(1-AGO)以便弱化随机序列的波动性和随机性,得到新的数列为
X(1)=(x(1)(1),x(1)(2),…,x(1)(n)),
其中[1]:
(2) 生成x(1)的邻均值等权数列
Z(0)=(z(0)(1),z(0)(2),…,z(0)(k)),
k=2,3,…,n
其中:
z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1),
k=2,3,…,n
(3) 根据灰色系统理论对x(1)建立关于时间t的白化形式的一阶一元微分方程GM(1,1),即
其中:α、μ为待解系数,分别称为发展系数和灰色作用量。
(4) 构造系数矩阵B和常数项Y,并求解微分方程的系数α、μ。矩阵B和常数Y分别表示为
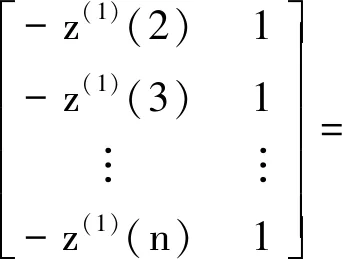
于是,原微分方程就可以表示为
Y=BU,
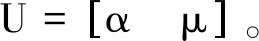
U=(BTB)-1BTY,
再将系数α、μ回代到原微分方程并求解,得到
根据x(0)(t+1)=x(1)(t+1)-x(1)(t),能得到预测值为
1.2 模型检验
GM(1,1)模型检验有3种方法:后验差检验、残差检验和关联度检验。GM(1,1)模型的精度通常用后验差方法检验。后验差检验是对残差分布的统计特性进行检验,它由后验差比值C和小误差概率P共同描述[10-11],其精度等级见表1。

表1 后验差检验法精度参照表
2 灰色BP神经网络组合模型
2.1 BP神经网络模型
BP神经网络是一种误差可反向传递训练的前馈网络,通过改进网络中隐含层的权重,使误差函数沿相反的梯度方向移动(最小梯度法)。BP算法有2个过程:信息正向传递和误差反向传递。
信息正向传递是将样本输入,传递到隐含层,通过激活函数,再传递到输出层,得到结果。误差反向传递是将正向传递的结果的误差反向传递到各个神经元,进而调整各个层的权重,直到误差降到可以接受的程度或者系统达到预设的训练次数。常用的BP神经网络有3层,即输入层、隐含层、输出层,每一层有若干个神经元,如图1所示。
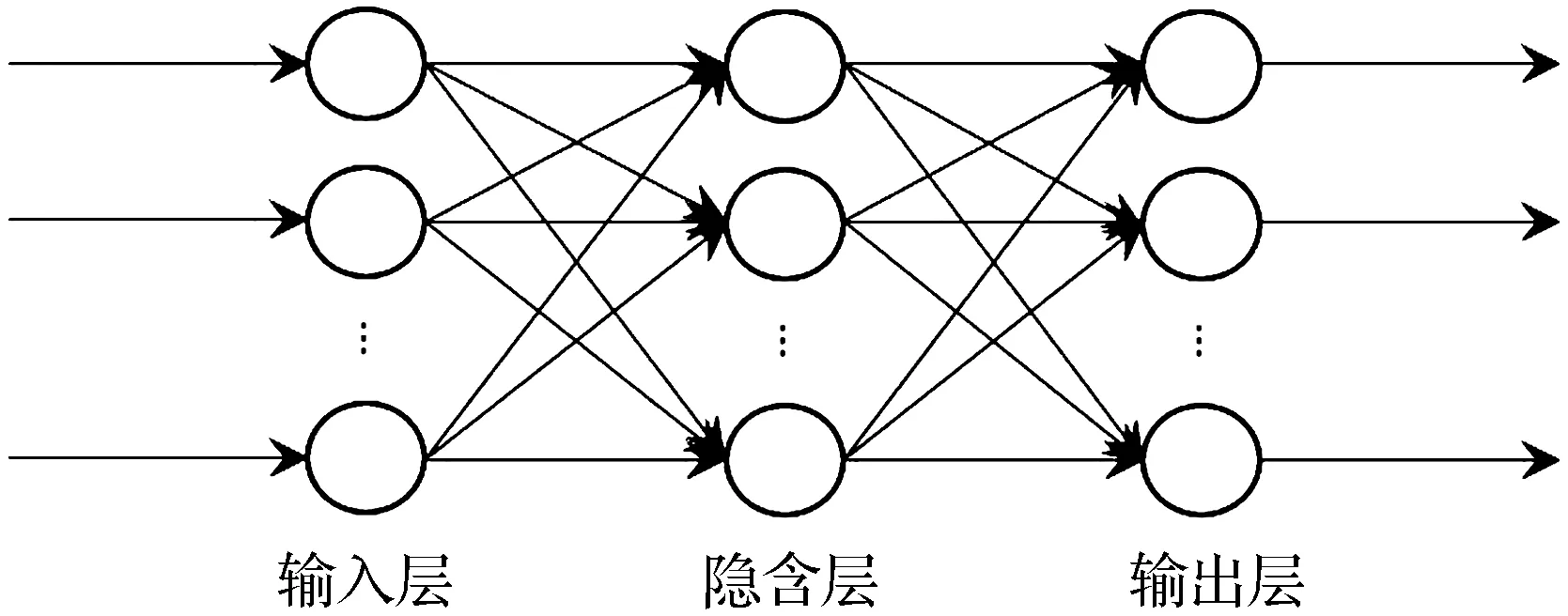
图1 BP神经网络结构Fig.1 BP neural network structure
2.2 灰色BP神经网络组合模型
灰色BP神经网络组合模型就是灰色系统理论模型和BP神经网络模型的结合,该模型既有灰色系统理论的灰色性,又兼具BP神经网络的自学习性和自适应性,能有效地处理非线性的数据序列[12-13]。具体建模过程如下:
(1) 设一组原始数据X(0)=(x(0)(1),x(0)(2),…,x(0)(n)),对其先用GM(1,1)模型,得到一组拟合数据Y(0)=(y(0)(1),y(0)(2),…,y(0)(n)),将拟合数据与原始数据作差,得到一组误差序列ε(0),即
ε(0)=X(0)-Y(0)。
(2) 以拟合数据Y(0)作为训练的输入样本,误差序列ε(0)作为输出样本,建立BP神经网络模型,并进行神经网络训练。
(3) 以拟合数据Y(0)作为预测样本,利用已经训练完成的BP神经网络进行预测,得到新的误差序列ε′(0),在此基础上得到预测值Z(0),即
Z(0)=Y(0)+ε′(0)。
3 实验分析
研究以某水电站大坝沉降监测项目为例,进行大坝沉降监测数据的预报与分析。截至2018年6月,该水电站已经有13期观测成果,以1~11期观测数据累计沉降量作为训练样本,对12、13期进行预测。观测数据及累计沉降量见表2。

表2 观测数据及累计沉降量
在利用灰色BP神经网络模型进行预测时,先以1~11期观测数据的累计沉降量建立GM(1,1),并预测12、13期的数据。预测结果见表3。再将GM(1,1)得到的1~11期累计沉降量的拟合值作为输入值,其残差作为输出值,建立BP神经网络模型。在本次建立的BP神经网络模型中,隐含层为5,训练次数为50 000,训练精度为0.005 mm。BP神经网络预测结果及与GM(1,1)对比结果见表4。
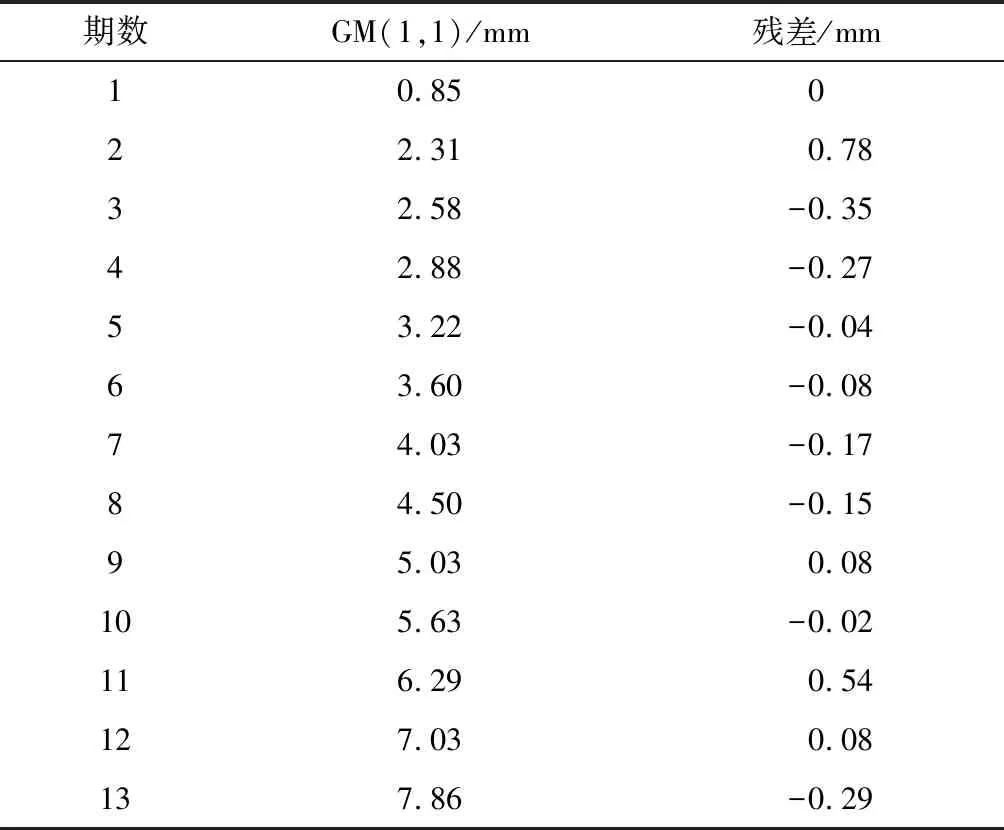
表3 GM(1,1)预测结果

表4 GM(1,1)和灰色BP神经网络模型结果对比
由表4可见,GM(1,1)模型预测值的最大残差为0.29 mm,而灰色BP神经网络模型预测值的最大残差为0.09 mm,残差仅为GM(1,1)模型的三分之一。所以利用灰色BP神经网络模型对大坝沉降监测进行预测,其拟合程度好、精度高。
4 结语
GM(1,1)模型适用于数据量少、不完整的数据序列,但是缺乏自适应性和自学习性,而BP神经网络模型刚好可以弥补这些不足,通过实例验证了灰色BP神经网络组合模型对大坝沉降数据预测精度较高。具体结论如下:
(1) 根据大坝沉降监测数据的预测结果和实测值,灰色BP神经网络组合模型的预测精度高于GM(1,1)模型的预测精度,几乎与实测值完全拟合。灰色BP神经网络同时涵盖了GM(1,1)模型和BP神经网络模型的优点,可以应用于大坝沉降监测的长期预测。同时也证明了组合模型预测精度高于单一模型预测精度。
(2) 灰色BP神经网络组合预测模型中训练次数较多,训练精度不够高,如何减少训练次数,提高训练精度,还需进一步的研究。
