六角形节块中子输运计算程序快速求解策略初步研究
2020-02-24夏文勇张滕飞刘晓晶熊进标
夏文勇 张滕飞 刘晓晶 熊进标 柴 翔
(上海交通大学核科学与工程学院 上海 200240)
核反应堆物理计算中,堆芯由不同的组件构成,若采用蒙特卡罗程序精细求解,计算时间开销较大,实际求解中可采用确定论中的扩散或输运方法。对于强吸收、高泄漏的中子学问题,往往需要采用较高精度的输运计算[1]。常用的中子输运方法包含有限元法[2-3]、离散纵标法[4]和节块法[5-6]等。其中,变分节块方法[7]为节块法的一种,它起源于20世纪90年代,该方法从二阶偶对称形式的中子输运方程出发,利用Galerkin变分和Lagrange乘子法在整个求解域建立一个包含节块平衡关系和边界条件的泛函,以空间上的正交多项式函数及角度上的球谐函数为基函数,采用Ritz离散方法展开泛函,获得中子通量密度及节块边界处偏中子流密度的节块响应矩阵,并迭代求解。
中子输运计算不可避免地存在计算量的问题,如何在保证输运方法计算精度的情况下减少计算时间,这极大地影响着输运方法程序的工程适用性。为提高变分节块法在低阶角度展开下的计算精度及计算效率,本文基于积分变分节块方法[8-9],以1/6堆芯计算替代全堆芯计算。当提高角度展开阶数时,程序求解时间将迅速增加。通过采用分布式存储方式MPI(Message Passing Interface)[10]使程序实现并行计算功能,以进一步减小计算时间开销。
1 理论模型

在各向同性散射假设下,三维中子输运方程可以写为:积分变分节块方法中,偶中子角通量密度ψ+可离散为[8]:

式中:Σt、Σs分别表示中子总截面及中子散射截面,m-1;q 为中子源项,m-3·s-1;φ 为中子标通量密度,m-2·s-1;x、y、z为标准正交的空间多项式向量;ψ+为偶中子角通量密度;f为空间基函数;ψ(Ω)为偶中子角通量密度展开矩,此时角度依赖关系以隐式形式写在展开矩中。
采用积分形式对输运方程进行变分并结合边界条件推导可得通量以及中子流密度方程(3)、(4):
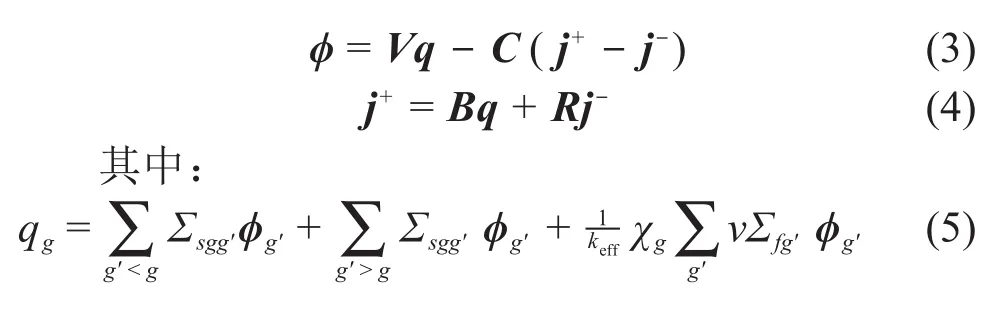
式中:V、C、B、R为响应矩阵,与各个节块内部的材料以及空间、角度离散的基函数等有关[8];φ为中子标通量密度的展开矩,φ=∫ψ(Ω)dΩ;q为中子源的展开矩;j±分别为出、入射中子流密度展开矩。由于离散形式的特殊性,V、C、B、R矩阵中包含形如∫dΩA(Ω)-1的矩阵运算过程,无法直接获得解析解,因此在计算过程中采用角度求积组对其进行数值求积分。在物理上,式(3)主要表征了节块内部的中子平衡关系,式(4)主要表征了节块表面的中子流连续性关系。
变分节块法的求解过程主要包含响应矩阵构造以及矩阵方程求解两个方面[11-12]。在响应矩阵构造过程中,不同典型节块(截面或几何区别于其他节块)以及不同能群构成了多套响应矩阵的集合(V、C、B、R作为一套响应矩阵集合)。不同的响应矩阵集合的计算过程之间具有天然的脱耦性,可以由多计算核心并行执行。
至于矩阵方程的求解,假设堆芯共有M层,每层径向由若干小正六边形组成。图1给出全堆芯及1/6堆芯在轴向第一层的排列方式。首先对六角形几何采用四色棋盘格式进行染色,即每个节块都标记为绿、红、橙、蓝中的一种颜色,保证相邻两个节块采用不同颜色。在所有节块内边界,以相邻节块的出、入射流作为耦合条件,而在外表面,认为节块自身是独立的,即随时可以根据边界条件和出射流更新其入射流。
在1/6堆芯计算问题中,图1靠近全堆芯中心处节块(如编号为1、2、3、……)的边界具有相邻节块和节块表面(节块及表面编号满足周期性对称条件),故实际求解中需假想求解域周围有一层节块包覆。图2展示了1/6堆芯中4色棋盘扫描及边界处理,并标明节块和节块表面编号。由图2(a)可知,节块表面所标记的6种颜色对应节块的6个表面;图2(b)中展示了求解域内节块1的径向6个面入射流均为节块2第一个面的出射流,这是由于在周期性对称条件下,求解域内节块2第一个面绕节块1的六个面逆时针依次旋转60°。节块(编号4、7、11、……)左边相邻的假想节块(编号2、3、5、……)所对应的表面编号为求解域内节块(编号2、3、5、……)表面编号逆时针旋转60°,轴向各层情形类似,不再赘述。
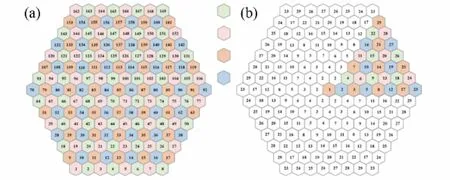
图1 全堆芯(a)及1/6堆芯(b)四色棋盘扫描Fig.1 Four-color scanning of full core(a)and 1/6 core(b)

图2 1/6堆芯四色棋盘扫描及边界处理(a)初始求解域布局,(b)考虑边界条件后求解域布局Fig.2 Four-color scanning and boundary processing of the 1/6 core(a)Initial solution domain,(b)Considering the boundary conditions
程序的串行[13]及并行计算策略如图3所示,串行计算将顺序执行,而并行计算则通过多进程进行单机或多机并行执行。假设节块数为N,能群数为G,则总的响应矩阵集合数目为N×G。在并行计算过程中,无论是全堆芯还是1/6堆芯计算,对于响应矩阵构造部分,若将N×G套响应矩阵均分给P个计算核心并行计算,则第p个核心所需计算的响应矩阵集合为:
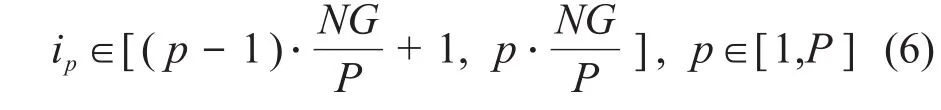
若N×G套响应矩阵不能均分给P个核心并行计算(负载不均衡),令NG-·P=n则第p个核心所需计算的响应矩阵集合为:

假设堆芯共包含28种典型节块及4群能群,因此共有112套响应矩阵集合。若分配给9个计算核心并行计算,则计算核心0~3各构造13套响应矩阵集合,计算核心4~8构造12套响应矩阵集合,引起负载不均衡,无法达到理想并行效率,此时理论上能达到的最高并行效率为(112/9)/13=95.7%。
对于矩阵方程求解部分,根据给定的计算核心数目,堆芯沿轴向自动划分相应数量的非重叠子区域。相同子区域内节块出射中子流作为相邻节块的入射中子流,不同子区域内节块出射中子流通过MPI通信传递给相邻子区域的相邻节块作为入射流。
2 数值结果
为验证加速求解策略正确性及其计算时间的优势,本文基于OECD/NEACRP发布的TAKEDA4基准题[5]进行数值准确性校核验证,并比较快速计算策略带来的时间效益。TAKEDA4是一个实验快中子反应堆(KNK-II),由于篇幅有限,本文仅对比控制棒半插情形,其堆芯径向及轴向结构如图4所示。堆芯共包含12个材料区,四群宏观截面,径向每盒六角形组件边长为7.5 cm,堆芯轴向总高度为190 cm。
由前述积分输运理论推导、1/6堆芯边界处理及并行区域分解,基于Fortran90编制了VITAS(Variational Integral Transport Analysis Solver)程序。VITAS程序可实现全堆芯及1/6堆芯求解,并可对此两种情形进行并行计算。程序将在并行环境下进行精度校核验算及计算时间测试,并行效率定义为:

式中:E为并行效率;T1为单核计算时间;T2为多核计算时间;P为处理器数目。
针对算例TAKEDA4,节块内部展开阶数为6,节块表面展开阶数为2,分别进行全堆芯(径向剖分为169个节块,轴向18层)、1/6堆芯(径向剖分为29个节块,轴向18层)两种情形计算,并与由蒙特卡罗程序GMVP提供的有效增殖因子(0.983 9±0.000 4)对比。
表1给出了堆芯在控制棒半插棒情形时,各区域平均中子通量密度的数值与参考值间相对误差。通过对比我们可以知道:两种不同尺寸的堆芯几何,在不同PN角度展开阶数下各区域的中子通量密度的误差基本一致,证明堆芯简化计算的正确性。当角度展开阶数为P1时,控制棒区G1能群处中子通量密度误差的绝对值最大,最大值为3.3%。若提高角度展开阶数至P3,误差降至1%。当角度展开阶数为P3时,平均中子通量密度的相对误差数值均控制在1.2%以内,表明积分方法具有很高的计算精度。

图3 串行(a)和并行(b)计算策略对比Fig.3 Comparison of serial(a)and parallel(b)computing strategies

图4 KNK-II实验快堆基准题堆芯布置图 (a)径向分布,(b)轴向分布Fig.4 KNK-II experimental fast reactor benchmark core layout (a)Radial distribution,(b)Axial distribution

图5 keff与PN展开阶关系Fig.5 The relationship of keffand PNexpansion order
图5给出了控制棒半插情形下堆芯有效增殖因子随PN开阶数的变化,从图5中可知,在各PN角度展开下,两种几何尺寸堆芯的有效增殖因子数值基本一致。PN展开阶数由P1增至P3,有效增殖因子与参考值误差迅速由441 pcm降至21 pcm,获得很好的计算精度。
表2是TAKEDA4在控制棒半插情形下,1/6堆芯及全堆芯中积分变分节块方法并行计算结果。其中,响应矩阵方程的求解部分采用了分块响应矩阵加速(PM[8]加速)。从可以看到,两种堆芯计算方式中响应矩阵构造时间基本一致,这是由于1/6堆芯改变的是堆芯几何尺寸,不影响典型节块数及能群数。响应矩阵构造部分的并行效率低下,一方面是由于并行效率不能达到理想值(3个计算核心时理论并行效率最高为98.25%,9个计算核心时理论并行效率最高为95.73%);另一方面是由于大维度数组的通信时间开销制约了并行计算带来的时间效益。在响应矩阵方程的求解中,由于堆芯尺寸仅为全堆芯的1/6,求解节块数目降低近5/6(522/3 042),故1/6堆芯求解时间开销较小。随着并行计算核心数目增加,总程序求解时间迅速下降,并行效率也随之降低。这主要是由于计算核心数目的增加导致通信开销增加,使得通信时间占比逐渐增大。1/6堆芯几何中,当并行核心数目为9时,随着角度展开阶数增加,并行效率并不单调:一方面是由于矩阵维度增加,通信时间开销增加;另一方面是由于分配给各计算核心的计算量增加,计算时间增加。所以并行效率是由计算时间与通信时间共同决定的。同时,并行效率还与并行机此时的数据传输速度(带宽)、磁盘I/O等有关。对于全堆芯几何与1/6堆芯几何计算,当并行计算核心数目为9、角度展开阶数为P5时,程序的总并行效率达到70%左右。

表1 KNK-II基准题半插棒情形时平均中子通量密度误差(%)Table 1 Error of average neutron flux density of the KNK-II benchmark rod-in-half

表2 TAKEDA4基准题两种堆芯尺寸下并行计算结果Table 2 Parallel calculation results of the TAKEDA4 benchmark under two core sizes
3 结语
本文从变分积分节块方法出发,采用60°周期性对称边界条件将全堆芯计算问题简化为1/6堆芯计算问题。通过比较两种几何尺寸下有效增殖因子及各区的平均中子通量密度,校核了1/6堆芯计算与全堆芯计算结果的一致性,并通过与GMVP蒙特卡罗程序结果做对比,验证了积分变分节块方法具有很好的计算精度。同时,初步实现对两种几何尺寸堆芯的并行计算。在9个计算核心并行下,相比单核全堆芯计算,1/6堆芯总计算时间开销在P1、P3、P5下分别约降低1/26、1/25、1/22,初步实现六角形节块的快速求解。以上计算并行效率总体偏低,如何提高程序的并行效率还需对并行算法及程序进一步优化。
