基于X射线荧光的扩散渗铝层厚度测量研究
2020-02-24刘吉超戴鹏里
刘吉超 汪 诚 戴鹏里
(空军工程大学 西安 710038)
航空发动机被誉为飞机的“心脏”,而涡轮叶片又作为发动机上工作环境最恶劣的部件之一,因此涡轮叶片的安全稳定工作对飞机的安全、可靠起着至关重要的作用。目前,发动机涡轮叶片的材料主要是高温镍基合金,这主要是因为该类合金能形成强化相:γ'相。K403镍基合金因其内部能形成较高含量的γ'相而被广泛运用于航空发动机涡轮叶片的制造[1-2]。然而,由于涡轮叶片在使用过程受到高温燃气的冲蚀,通过在涡轮叶片表面采用渗铝处理可以有效提高其在实际服役环境中的抗氧化性能。然而,不同的处理参数将对渗层的质量产生明显影响,从而影响渗铝叶片的实际工作性能。
叶片表面渗铝层厚度的均匀性是影响渗层质量的重要参数之一,渗铝层厚度不均匀会导致叶片传热、受力不均匀,影响叶片的使用寿命,对发动机的使用造成严重安全隐患。但目前尚未出现能够对扩散型渗铝层进行无损检测的计算方法以及相关设备。常用的涂、镀层厚度检测方法有超声检测法、磁检测法、涡流检测法等,但是这些方法都受到涂层以及基体材料性质的制约[3-4],无法实现扩散型渗层厚度的准确测量。目前用于检测叶片表面扩散渗铝层厚度的方法主要为断面扫描法,该方法将破坏待测部件的完整性,且无法实现对叶片不同部位表面渗层的全面检测。
随着核技术发展,射线检测技术在各领域得到广泛的运用[5-7],被用于不同领域金属基体上各类涂层厚度的无损测量之中,其中X射线的运用最为广泛。Cao等[8]在1989年对X射线荧光吸收法测量薄层厚度进行理论分析并运用实验数据验证了相关理论的正确性。随后该方法被广泛地运用于涂、镀层厚度的研究当中;娄凤君等[9]实现了一种X射线荧光测厚仪的研究;黄明等[10]利用此方法实现了铜铁样品上油漆层厚度的测量;Nogueira等[11]也开展了钢板上油漆层厚度的测量研究,研究表明:X射线荧光测厚方法与磁测厚法测量结果偏差不超过1%。Lopes等[12]实现了文化遗物上镀金层厚度的测量。到目前为止,虽然已经有很多研究人员开展了基于X射线表面涂、镀层厚度测量的方法研究,但是还没有关于扩散型渗铝厚度测量相关的研究报道。扩散型渗层由于在加工过程中金属原子自由运动造成渗层范围内元素含量、密度等相关参数均在不断变化,这给扩散型渗层厚度测量带来了很大的影响。本文将以X射线荧光吸收法为基础,根据其截面沿深度方向的化合物分布[13]将K403合金扩散渗铝层简化成基底-涂层模型,再开展相关计算模型研究。具体实施过程如下:首先制作标准试样,并利用扫描电镜观察截面,对试样渗层厚度进行标定;然后开展K403合金基体内部主要元素相关的一元计算模型分析;再进一步开展多种元素综合的多元模型分析;最后开展两类模型之间的对比研究,得到一种较为有效的扩散型渗层的检测计算模型以及分析方法。通过该理论计算方法,可以为实现叶片表面扩散型渗铝层快速无损检测打下基础。
1 材料与方法
1.1 实验材料及试样制作
本文采用由多种元素综合强化形成的K403镍基高温合金表面渗铝试样,其中基底K403合金的主要化学成分如表1所示[14]。

表1 K403合金试样成分(%)Table 1 Composition of K403 alloy(%)
在本文中为提高测试结果的准确性,排除荧光测试点选择的随机性,本文将试样制作成尺寸为1 mm×10 mm×3 mm的长条状试样并规定荧光测试点位置不得距离扫描电子显微镜(Scanning Electron Microscope,SEM)观测截面超过1 mm,示意图如图1所示。此外,为了实现对K403合金渗铝涂层的检测,本文选取不同厚度的K403合金渗铝试样作为研究基础,试样厚度值如表2所示。其厚度值的标定采用SEM观测的方法确定。
1.2 测试方法
采用日立SU-1510型扫描电镜对渗层厚度进行测量和标定。采用一六XAU型X射线荧光测厚仪对不同厚度的渗铝试样进行荧光检测,选取的管压25 kV,准直器大小ø0.5 mm,单点测量时间30 s,单个试样测量次数为10次,每个试样记录的荧光强度值为10次测量结果的平均值。

图1 试样示意图Fig.1 Schematic diagram of test sample
利用SPSS 25.0软件对实验数据进行拟合计算。SPSS软件是一种统计分析软件,能够实现任意大小数据文件的处理。在实际的使用过程中,只需要通过输入数据然后选择相关的回归分析方法就能准确快速地实现数据分析。
2 结果与讨论
2.1 结构模型简化与计算理论基础
图2表示了K403高温合金渗铝试样截面的渗铝层SEM以及能谱仪(Energy Dispersive Spectrometer,EDS)分析。从试样各元素沿深度方向的能谱变化以及截面形貌可以看出,沿渗铝层深度方向上各元素含量不断变化,并且渗铝层区域与基体的形貌图有所差别,这主要由于各元素含量比例不同导致渗层和基体中形成的主要相有所差别。因此,将K403合金渗铝试样结构模型简化为K403高温合金基体上涂了一层Al含量沿深度方向不断变化的合金涂层。此外,由于试样中渗铝层厚度远小于初级射线所能穿透的深度以及渗铝层中存在的主要元素为Al,所以此计算模型忽略由渗层中元素激发的荧光对实验结果的影响,即将渗铝层厚度为0 μm的K403合金所激发出来的各元素荧光强度作为不同厚度渗铝试样的初始荧光荧光强度I0。其简化的结构模型以及测量原理如图3所示。

图2 试样渗铝层SEM及EDS分析 (a)~(f)分别反映了Al、Ni、Cr、Co、Mo、Ti沿渗层深度方向能谱图Fig.2 SEM image and the EDS analysis of aluminizing layer (a)~(f)Respectively reflect the X-ray photoelectron spectroscopy ofAl,Ni,Cr,Co,Mo,Ti along the depth of aluminizing layer
X射线荧光吸收法是测量涂镀层厚度的一种常用方法,当X射线荧光穿透不同厚度的涂镀层时,其荧光强度值呈现指数衰减的趋势,如式(1)所示。本文将以此公式为基础,并基于图3所示的渗铝层模型简化假设和测量原理,根据最小二乘法确定扩散型渗层的吸收系数,建立相应的计算模型。

图3 简化模型及测量原理Fig.3 Simplified model and measurement principle

式中:I0表示基体元素辐射出来初始荧光强度值;x表示基体表面扩散型渗层的厚度;μ表示渗层对元素的线性吸收系数;IF表示探测器接收到各元素的荧光强度值大小基。
将式(1)右边同时除I0得到IF/I0,令R=IF/I0,将R记做元素的强度比。
然后将同除I0后的等式两边同时取对数,将lnR记做强度比对数值,得到式(2)。

通过式(2)可知,在吸收法计算公式下,强度比的对数值lnR是关于涂层厚度x的一次方程。因此,可以利用线性回归的方法拟合得到系数,建立关于扩散型渗层的厚度测量的数学计算模型。
2.2 实验数据准备
首先,根据表1,本文选取了Cr、Ti、Ni、Co、Mo元素的荧光强度值作为实验的记录值,最终的荧光强度值为10次测量结果的平均值,其中未记录W元素荧光强度的原因在于W原子序数较高,激发时所需的能量较高,并且其一般作为X射线管的靶材。然后测试得到不同渗铝层厚度下的主要元素的荧光强度值,并通过计算得到不同厚度下各元素强度比的对数值如表3所示。此外,按照实验数据量80%用来标定模型,20%用来进行模型测试[15],在表3中随机选取序号为3、10、13、19的4组数据进行模型验证,其余数据用来进行模型标定。

表3 试样中主要元素的荧光强度比对数值(lnR)Table 3 Log of fluorescence intensity ratio of the major element in the sample
2.3 模型的建立与验证
2.3.1 一元线性回归
根据式(2)可知,lnR与涂渗层厚度x之间是线性关系,因此本文将首先以该方程以及最小二乘法相关理论为基础分别建立Ni、Cr、Co、Mo、Ti元素强度比对数值(lnR)为变量的一元线性回归计算模型,并且对不同元素拟合结果的精确度进行检验。
以表3中数据为基础,利用SPSS软件拟合得到5种元素分别对应的计算模型,同时,根据式(2)可知,强度比与涂层厚度之间的关系式不存在常数项,所以建立模型时,规定模型经过原点,其计算模型如表4所示。

表4 各元素相应的一元线性回归计算模型Table 4 The corresponding unitary linear regression model of each element
当相关系数越接近于1时说明模型拟合结果线性度越好。从表4结果可知,以lnRTi作为变量的计算模型相关系数为0.866,明显低于其余4种模型,说明渗铝层厚度与Ti元素强度比对数值(lnRTi)之间的线性关系不明显,因此,在计算中不考虑lnRTi这一变量的实验计算模型。此外,在其他4种模型下的相关系数均非常接近于1,其中Mo元素的相关系数最高。
以表4中建立的数学计算模型为基础,利用序号为3、10、13、19的试样对建立的计算模型精确度进行检验,结果如表5所示。
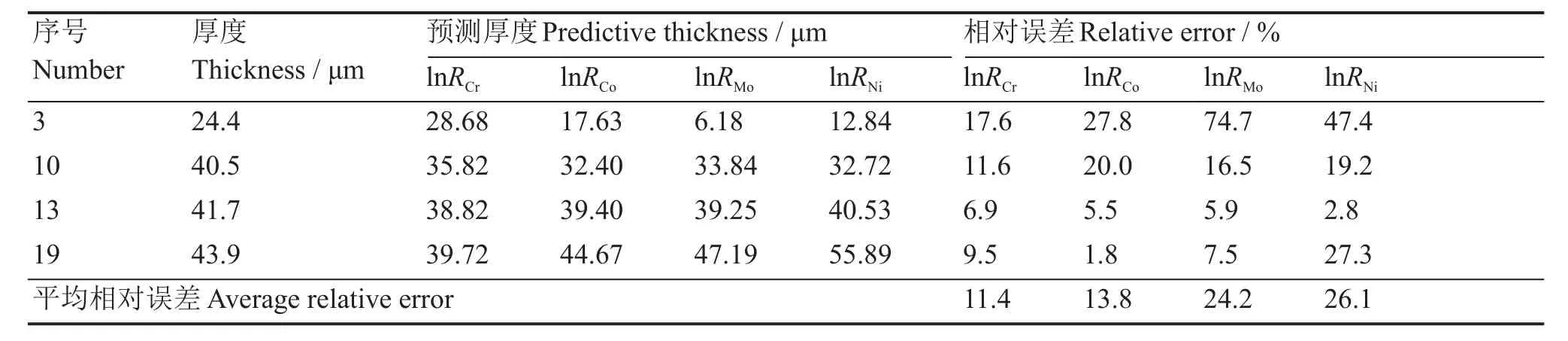
表5 各元素相应一元模型预测厚度及其相对误差Table 5 Predictive thickness and relative error of unitary model corresponding to each element
从表5中可以看出,通过Cr元素荧光强度建立的回归模型拟合结果最好,Co元素次之,Mo和Ni元素建立的模型引入的相对误差均较高。因此,从建立一元线性回归模型的角度来看,以Cr和Co元素的荧光强度值建立的计算模型结果相对更加准确,其引入的平均相对误差分别为11.4%和13.8%,明显低于另外两种一元线性回归模型。此外,对不同元素建立的一元计算模型而言,其引入的相对误差随厚度的变化波动较为明显,并且处于薄渗层处的相对误差明显高于厚渗层处的相对误差。利用单元素荧光强度建立的一元回归模型误差较大的原因在于K403合金渗铝工艺的实质是金属原子的自由扩散,在渗层区域也存在基体中的金属元素,并且在实际生产过程中受到温度、时间等条件的影响,试样中金属原子扩散的均匀程度不一致,导致渗层内部的元素分布存在差异,这些元素分布的变化最终直接反映在各元素荧光强度值的变化上。通过以上研究说明运用X射线荧光吸收法解决K403合金扩散渗铝涂层厚度无损检测的可行性。
2.3.2 基于向前选择变量法的多元线性回归模型
从对一元线性回归计算模型的研究中可以看出,根据不同元素建立的计算模型对最终测量结果的精确性影响很大。此外,在实际的运用过程中如果对每一种元素均进行建模分析将带来巨大的工作量,并且建立的模型计算精度也不能较好满足测试精度的需求。因此,本文将以式(2)为基础,建立一种基于多元素综合的回归计算模型。多元回归计算模型将综合考虑由各种元素变化而引起的实验结果影响,一定程度上可以避免由于渗铝扩散过程中某一种金属原子的突然变化对实验测试结果造成的较大误差。
在开展多元回归分析时,自变量的选择对实验结果的精确性有着很大的影响。目前常用的自变量选择方法有很多,其中最为直接的一种就是穷举法[16],该方法将充分考虑在所有变量存在的组合,对每一种组合进行单独分析,并对计算模型进行分析,但是,当模型中变量个数过多时,该方法将没有办法运用。此外,在多元回归计算分析的运用过程中,其他较为有效的变量筛选方法得到了发展,其中较为常见的方法有向前选择变量法、向后删除变量法、逐步回归法等[16]。这几种方法均能较为有效地筛选出对结果影响较大的变量。本文将以向前选择变量法为基础实现变量的选择。
向前选择变量法将变量个数实现从无到有的过程。首先对每一个自变量的一元线性模型进行F检验,将F值最高的变量选入模型,作为模型中的第一个变量。然后对剩下的变量进行偏F检验,同样选出通过偏F检验并且F值最大的变量,以此类推,直到所有的变量均不能通过偏F检验。
以表3中的数据为基础,利用SPSS软件建立基于向前选择变量法的多元线性回归模型,其中同样设置截距为0,以确保强度比对数值为0时渗铝层厚度为0。在建立此模型过程中,选择扩散渗铝层厚度(x)为因变量,各元素荧光强度比对数值(ln(R))作为自变量,建立的多元线性回归模型如式(3)所示。


表6 基于向前选择变量法的回归分析结果Table 6 Regression analysis results based on forward selection variable method
从表6中可知,方差分析的显著性均为0,在系数的显著性分析中,除变量lnRMo引入的显著性高于0.05以外,其余两种变量引入的显著性均低于0.05,这说明除lnRMo以外的其余系数的显著性均较高。此外,通过表6也可以得出,回归模型与显著性均满足F检验和t检验。从向前选择变量方法建立的数学模型可以看出,lnRMo与lnRCr对结果起负向作用,这与荧光吸收的基本理论保持一致;然而,ln(RTi)对模型起正向作用,这说明在此模型中将变量ln(RTi)理解为模型中的修正变量,因此在该计算模型中准确获得Ti荧光强度值随厚度变化趋势对模型的准确性起着重要的作用。此外,从标准化系数大小可知,对扩散渗铝层厚度模型影响较大的变量是lnRCr,这与一元回归模型中以lnRCr建立的数学模型精确度最高的结果相对应,这说明以Cr元素相关的荧光强度值对计算模型的精度起着主导作用。
通过式(3)给出的多元回归的计算模型,对序号为3、10、13、19的试样可以计算得到如表7所示的预测结果。结果表明:多元回归模型的建立有效地提高了测试结果的精确度,所有验证试样的相对误差均小于10%,其中,序号为10的试样的相对误差最大,为6.2%,4组试样的平均误差仅为3.2%,该测试结果能基本满足测试的需求。

表7 多元回归模型预测厚度及相对误差Table 7 Predictive thickness and relative error under multiple regression
2.3.3 模型对比分析研究
图4表示了不同计算模型下不同标准厚度试样的相对误差变化,从图4中可知,在一元回归计算模型中,薄渗层处测量的相对误差值均远大于厚渗层,但是多元回归模型的建立有效降低了薄渗层试样的相对误差;从不同计算模型对应的各渗层厚度的相对误差来看,多元回归模型对应不同厚度试样的相对误差大小分散度更低,这说明运用多元回归能有效提高模型的稳定性;多元回归模型在4种渗铝层厚度试样下的平均误差值远小于一元回归计算模型。因此,多元回归模型的运用能更加有效地解决扩散渗铝层厚度的无损测量,同时,多元回归模型具有较高的稳定性,这主要是因为多元素的综合分析不会因其中某一种元素荧光强度值的变化而对最后的测量结果造成较大的影响。
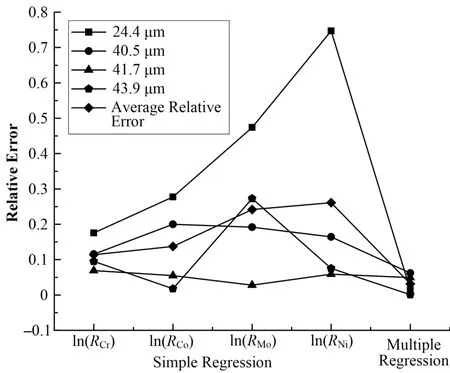
图4 各模型相对误差对比Fig.4 Comparison of relative errors of each model
3 结语
针对扩散渗铝层这种特殊的渗层,本文采取了X射线荧光吸收法开展了两种不同的计算模型的对比研究,通过研究得到以下结论:
1)以简化的涂层结构模型和吸收法为基础建立的数学计算模型基本能实现扩散渗铝层厚度的测量;
2)以单一元素建立的渗层厚度计算模型容易产生较大误差并且误差值随厚度的变化而发生较大的波动,此类模型测量的稳定性较差,不利于扩散型渗层厚度的测量;
3)以向前选择变量法建立的多元回归计算模型能有效地解决一元回归模型带来模型测量结果误差大的问题,该类模型带来的预测值平均相对误差仅为3.2%,并且该类模型计算渗层厚度的稳定性较好,相对误差值不会出现较大的波动,基本满足扩散型渗层厚度的无损检测需求。
通过以上的结论可以看出,采用多元综合分析的方法更能较好解决K403合金渗铝层厚度测量问题。
