利用拉普拉斯能量和CNN的多聚焦图像融合方法

翟 浩，庄 毅

(南京航空航天大学 计算机科学与技术学院，南京 211106)

在数码摄影中，由于光学透镜的有限景深，很难获得一幅所有相关目标都聚焦的全聚焦图像.一般情况下，只有位于焦平面上的目标是聚焦的或者清晰的，而位于焦平面其它位置例如焦平面之前或者之后的目标则都是离焦的或者模糊的.多聚焦图像融合技术是是一种有效的可以合成相同场景下不同聚焦设置采集到的多幅源图像，获得一幅单一的具有扩展景深的融合图像.目前，多聚焦图像融合技术已经应用到了大量的应用领域，例如显微成像、数码摄影、视频监控以及计算机视觉等领域[1].近些年，出现了大量的多聚焦图像融合方法.根据空间域的不同，这些融合方法大致可以分为两大类：基于变换域的方法和基于空域的方法[2].

基于变换域的融合方法一般主要包括三个步骤：分解、融合和重构.基于稀疏特征矩阵分解和形态学滤波的多聚焦图像融合方法被提出来[3].该方法通过将源图像进行稀疏特征分解形成稀疏特征矩阵，然后对该稀疏特征矩阵进行加权形成一个临时矩阵，最后对该临时矩阵进行形态学滤波，再结合基图像，形成最终的融合图像.接着，基于图像分解的多聚焦图像融合方法被提出来[4]，该方法通过使用改进的迭代重加权分解算法将源图像分解成卡通分量和纹理分量，然后对卡通分量和纹理分量分别进行融合，形成最终的融合图像.此外，基于多级形态分量分析和支持向量机的多聚焦图像融合方法被提出来[5]，该方法通过使用多级形态分量分析分解源图像，并从自然层提取特征向量.然后使用训练过的二类支持向量机对这些特征向量进行分类，最后融合系数形成最终的融合图像.这类融合方法极易导致最终的融合图像产生对比度或者清晰度下降的问题.

同基于变换域的方法相比，在基于空域的融合方法中，融合规则直接应用到像素、子块和区域的.根据聚焦度量方法，选择具有较高清晰度的像素、子块或者区域进行重构来形成最终的融合图像.一种基于四叉树结构利用权重聚焦度量的多聚焦图像融合方法被提出来[6]，根据有效的四叉树分解策略，把源图像分解成四叉树结构下最优尺寸的子块，采用权重修改拉普拉斯和来检测清晰区域，并将这些清晰区域组合成全聚焦图像.接着，基于多尺度形态学聚焦度量寻找边界的多聚焦图像融合方法被提出来[7].该方法通过采用一种形态学聚焦度量方法来获取边界区域和非边界区域，然后采用融合方法对边界区域和非边界区域分别进行融合.其中，最具代表性的是基于梯度信息的方法[7-8]和基于深度学习的方法[9-11].在基于空域的融合方法中，由于分割区域的形状或者聚焦度量准则难以确定，所以基于空域的融合方法通常很难精确的获得精确的分割边界，并且最终的融合图像在分割边界附近将会产生严重的伪影效果.

针对以上问题，利用拉普拉斯能量和CNN的多聚焦图像融合方法被提出来，该方法的优势主要体现在以下三方面.第一，直接采用源图像中的像素进行融合，克服了融合图像中清晰度或者对比度下降的问题.第二，采用拉普拉斯能量作为聚焦度量法则，可以有效的提取源图像中的细节信息，这对于选择更高清晰度的子块至关重要.第三，由于训练后的卷积神经网络模型具有很强的学习子块相对聚焦度的能力，因此该方法可以获得非常精确的分割边界.

1 提出的方法

目前，卷积神经网络已经广泛应用于计算机视觉的大量应用领域，例如脸部检测[12]、脸部识别[13]、超分辨率[14]以及块相似性对比[15]等等.受卷积神经网络模型在特征提取和分类中具有强大能力的启发，利用拉普拉斯能量和CNN的多聚焦图像融合方法被提出来.在本研究中主要探讨两幅源图像的融合问题，多幅源图像的融合问题可以按照两幅源图像的融合顺序依次进行融合.提出方法的框架如图1所示.从图1中可以看出，提出的方法主要包括5个阶段：聚焦度量、CNN聚焦、二值分割、小区域滤波和融合阶段.

接下来，详细的展示多聚焦图像的融合过程，将采用Lytro数据集中的“child”图像作为实验对象，提出方法的融合过程如图2所示.首先对源图像进行聚焦度量，分别获得两幅源图像对应的聚焦信息图.根据栅栏扫描的顺序，采用滑动窗口依次获取聚焦信息图的对应子块.同理，通过滑动窗口的不断采样，用于获得聚焦信息图中所有的样本数据.把这些样本数据反馈至训练后的CNN模型，获得这些样本数据的预测标签值.对这些标签值重新排列成源图像的尺寸，获得聚焦图.最后，对聚焦图进行二值分割和小区域滤波的处理，获得一个正则化的最终决策图.根据最终决策图对两幅源图像进行融合，形成最终的融合图像.

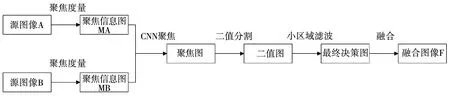
图1 提出方法的框架

图2 提出方法的融合过程

1.1 训练样本集

根据文献[16]中的客观度量，EOL是空域融合方法中首选的聚焦度量方法.对于每个像素，计算获得的EOL作为该子块拉普拉斯的局部平均值.因此，获得聚焦信息图的公式如式(1)所示.其中H是平均滤波器，⊗和2分别表示卷积运算和拉普拉斯运算.对于滤波器H，高斯滤波器的尺寸为5*5，并且靠近局部窗口中心的拉普拉斯值大于远离局部窗口中心的拉普拉斯值.具体的计算公式如式(2)所示.对于由两个变量i和j构成的一幅数字图像，拉普拉斯是最简单的各向异性的导数运算.

M=H⊗(2×I),

(1)

(2)

聚焦信息图展示的是源图像的高频信息，在清晰区域具有较大的值而在模糊区域具有较小的值.两幅源图像的聚焦信息图如图2所示，清晰区域包含更多的细节信息，而模糊区域则是相反的.在对聚焦信息图计算完后，创建训练样本集来对CNN模型进行优化.对于每一对源图像，采用滑动窗口的方式依次获取对应的聚焦信息图子块.

多聚焦图像融合问题可看作是一个二类分类的问题.为此，使用大量的训练样本数据作为训练对象，每个相同场景的对应子块作为一组训练数据.对于一个样本{pA,pB}当pA比pB更加清晰，则该样本被认定为正向样本，并且该样本的标签值设定为1.反之，当pB比pA更加清晰，则该样本被认定为负向样本，并且该样本的标签值设定为0.使用常用的灰度多聚焦图像集作为训练样本数据.对于彩色图像，首先要转化成灰度图像.对于每对多聚焦图像对，随机从多聚焦图像集中选取尺寸为16*16的块作为采样数据.在本研究中，最终的训练样本数据共包含500 000个正向样本和500 000个负向样本.

1.2 网络结构

首先，面临的重要问题就是窗口尺寸的问题.当窗口尺寸过大或者过小，生成的聚焦图都不会很理想，只有合适的窗口尺寸才能获得最好的效果.当窗口尺寸过大，活跃窗口更容易同时包含聚焦区域和离焦区域，导致融合图像的分割边界不精确.当窗口尺寸过小，CNN模型的分类准确率会降低，这样会导致大量的标签误选.基于以上考虑以及窗口尺寸的实验，当设置窗口的尺寸为16*16时，获得的聚焦图效果最好.

其次，当使用CNN时，需要先确定CNN的网络结构.提出方法的网络结构如图3所示.该CNN的网络结构共包含5层，其中包含1个输入层，3个卷积层和1个最大池层.第1层是输入层.输入是聚焦信息图对应的子块，其尺寸为16*16.第2层是卷积层.使用尺寸为3*3和幅度为1的卷积核对输入子块进行卷积.卷积后获得16个特征图，其中特征图的尺寸为14*14.第3层是卷积层.同样使用尺寸为3*3和幅度为1的卷积核对第2层输出的特征图进行卷积运算.卷积后获得32个特征图，其中特征图的尺寸为12*12.第4层是最大池层.使用尺寸为2*2和幅度为2的下采样核来对第3层输出的特征图进行最大池运算，池运算后可以获得32个特征图，其中特征图的尺寸为6*6.第5层是卷积层，使用尺寸为3*3和幅度为1的卷积核对第4层的特征图进行卷积运算.卷积后获得64个特征图，其中特征图的尺寸为4*4.接下来，对每个分支的64个特征图进行连接形成一个尺寸为[2 048，1]的特征向量F1.然后对该特征向量进行全连接运算，形成一个尺寸为[2，1]的特征向量F2.最后使用Softmax函数对该特征向量F2进行计算，形成尺寸为[2，1]的特征向量F3.该特征向量F3的每个值分别表示属于各个类的概率.

1.3 训练模型

在训练过程中，对于一个样本数据，首先把该样本数据先转化成活跃窗口WA和WB，然后采用前向传播和反向传播两个阶段来进行卷积神经网络模型的参数优化.卷积层的前向传播见式(3).其中，Xi为第i个输入特征图，Kij为第i个输入特征图和第j个输出特征图对应的卷积核，而bj为第j个输出特征图的偏置值.此外，n为输入特征图的个数，f函数为Relu激活函数，并且符号×表示的是卷积运算.

(3)

前向传播过程中的池化层可以看作是一个下采样层.对于下采样层来说，输入特征图和输出特征图的个数是相同的，只是输出特征图的尺寸变小了.池化层的运算一般有两种：最大池和平均池.池化层的运算一般是对输入图像的不同子块获取其最大值或者平均值，来作为该子块的输出值.每个输出图都有一个乘性偏置β和一个加性偏置b.池化层的前向传播见式(4).其中，down()表示一个下采样函数.

(4)

(5)

全部训练集上的误差其实就是每个样本误差的总和，因此N个样本的总误差如式(6)所示.

(6)

假设W表示所有待优化参数组成的向量.若能从中找出一组参数W*来最小化EN，那么该组参数W*则为所要寻找的最优参数，如式(7)所示.

(7)

由于EN中的参数过多，所以一般的方法很难求得其最小值.对此，一般都是使用梯度下降的方法来进行求解，具体求解过程如式(8)所示.其中，α为学习效率.EN直接对参数求导是十分复杂的，所以先用EN对输入加权和求导，在用输入加权和对参数求导.至此，卷积神经网络的所有参数优化完成.

(8)

1.4 决策图正则化

将多聚焦源图像对反馈至训练后的CNN模型，获得一个聚焦图.此时的聚焦图中还存在一些误判的标签.采用“选择最大”的策略来对聚焦图进行进一步的修正，有助于去除聚焦图中一些误判的标签，进一步完善聚焦图.使用设定的阈值来对聚焦图进行分割形成二值图，详细的计算过程如式(9)所示.其中，M表示聚焦图，B表示二值图，并且T表示设定的阈值.本文中设定的阈值为0.5.

(9)

此时，二值图中仍然存在一些类似“孔洞”的小区域，通过小区域滤波可以有效的处理这些“孔洞”问题.具体来说，在二值图中小于阈值面积的区域需要进行反转.通常情况下，当图像中区域的面积<0.01×H×W时，该区域相对于整幅图像来说属于较小的区域.其中，H和W分别表示每幅源图像的高度和宽度.因此，把区域面积尺寸<0.01×H×W的区域认定为小区域，通过对这些小区域的去除形成最终决策图.

最后，根据最终决策图提供的权重分配图，对多聚焦源图像进行融合.具体的融合规则如式(10)所示.其中，多聚焦源图像分别为A、B，最终决策图为D，而最终的融合图像为F.如果多聚焦源图像是彩色图像，使用最终决策图的分配权重分别对彩色图像的各个通道进行融合.最后，重新组合各个融合后的通道形成最终的融合图像.

F(x,y)=A(x,y)×D(x,y)+B(x,y)×

(1-D(x,y)).

(10)

2 实验

2.1 实验设置

在本实验中，提出方法的有效性主要是通过两组不同的公开图像数据集进行验证.第一组采用的是常用的灰度图像数据集，包含20对不同尺寸的常用多聚焦灰度图像对.第二组采用的是Lytro彩色多聚焦图像数据集，共包含20对尺寸为520*520的彩色图像.图4展示了本文所采用的部分灰度多聚焦图像数据集和Lytro彩色多聚焦图像数据集.与最近提出的一些图像融合方法PCNN[17]、PC[18]、FFIF[19]、BFM[7]和CNN[9]进行对比，来展示提出方法的优越性.

近年来，对融合图像的质量进行评价，提出了许多客观度量指标.本文所采用的客观度量指标包括以下4个.第1个指标采用的是归一化互信息指标[20]QNMI.该度量指标主要是测量源图像和融合图像的相关程度，即源图像传递到融合图像的原始信息量.QNMI的公式如式(11)所示，其中H(IA)、H(IB)和H(IF)分别表示源图像A、B和融合图像F的信息熵，而MI(IA,IF)和MI(IB,IF)表示的是源图像A、B与融合图像F的互信息.

(11)

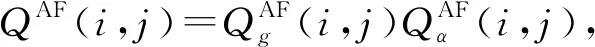
图4 部分多聚焦图像数据集

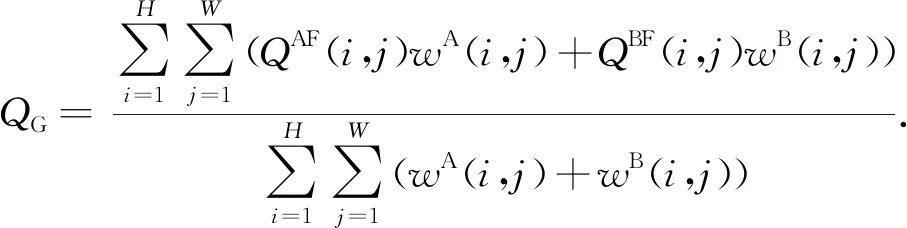
第3个指标采用的是基于结构相似性的度量指标[22]QSSIM.该指标主要是用来度量源图像和融合图像的结构相似性.QSSIM的式如(13)所示，并且λ(w)的式如(14)所示.其中，s(A|w)和s(B|w)是A和B在局部窗口w的活跃程度.

(13)

(14)

第4个指标采用的是基于人类视觉度量的指标[23]QHP，该指标主要是用来度量源图像和融合图像的人类视觉系统中主要特征的相似性.全局质量图QGDM的公式如(15)所示，其中，QAF(i,j)表示从源图像A传递到融合图像F的对比度，QBF(i,j)与QAF(i,j)的定义是相同的.λA和λB分别是QAF(i,j)和QBF(i,j)的显著图.全局质量图QGDM的平均值作为QHP的度量值，如式(16)所示.

QGQM(i,j)=λA(i,j)QAF(i,j)+λB(i,j)QBF(i,j),

(15)

(16)

2.2 实验结果与讨论

2.2.1 视觉效果对比

展示提出的方法可以生成具有良好视觉效果的融合图像，分别选择具有代表性的灰度图像“disk”和Lytro彩色图像“child”进行实验.以“disk”为实验对象，本文方法与其它图像融合方法的实验结果如图5所示.从图5中可以看出，PCNN方法的融合图像在钟表的边框产生了较为严重的失真，并且也伴有明显的对比度下降.PC方法中的融合图像在钟表的边框上方产生了大面积的模糊效果.QT方法的融合图像则是在钟表的上边框产生了小面积的模糊效果，而且在钟表的左表框产生了两个严重的缺口.BFM方法的融合图像在钟表边框上方产生了较为严重的伪影.FFIF方法的融合图像在钟表的左边框产生了两个较为严重的缺口.CNN方法的融合图像在钟表的左边框产生了明显的伪影效果.同其它的图像融合方法相比，提出的方法则是展现了较好的融合效果.

图5 不同图像融合方法的“disk”融合效果

对本文方法的融合性能进行测试，有必要对彩色图像数据集Lytro进行实验验证.以“child”图像作为实验对象，不同图像融合方法的实验结果如图6所示.从图6中可以看出，PCNN方法的融合图像具有明显的失真.PC方法的融合图像在耳朵上方和分界区域出现了大面积的模糊效果.QT方法的融合图像在一些区域产生了明显的伪影效果.BFM方法的融合图像不仅在耳朵上方产生了严重的模糊效果，而且在分界区域也产生了明显的伪影效果.FFIF方法的融合图像在很多区域都产生了严重的伪影效果.CNN和提出方法的融合效果较好，具有良好的视觉效果.不同图像融合方法的性能通过对不同融合方法的最终决策图进行展示，如图7所示.从图7中可以看出，与其它图像融合方法相比，CNN和提出的方法获得了更精确的最终决策图.

图6 不同图像融合方法的“child”融合效果.

2.2.2 定量比较

更加客观的对不同图像融合方法的性能进行对比，使用QNMI、QG、QSSIM和QHP等4个评价指标来评价不同图像融合方法的性能优劣.对于灰度多聚焦图像数据集，不同图像融合方法的客观度量指标的平均值如表1所示，每一项评价指标中最好的结果用粗体表示.从表1中可以看出，本文提出方法的实验结果优于其它图像融合方法.

图7 不同图像融合方法的最终决策

表1 不同图像融合方法在灰度多聚焦图像集的客观度量结果

对于Lytro彩色图像数据集，不同图像融合方法的客观度量指标的平均值如表2所示.从表2可以看出，提出的融合方法在Lytro数据集上也展现出了较好的实验结果.更清晰的展示提出方法的优越性，对两个数据集进行整体分析.其中，不同图像融合方法在整个数据集上的客观度量指标的平均值如表3所示.

2.2.3 中间融合结果以及多幅源图像的融合

提出的方法在多聚焦图像融合的有效性，对6对多聚焦源图像的中间融合结果进行展示，如图8所示.从二值图可以看出，聚焦图中的大部分像素都进行了准确的分类，只有平滑区域的一些标签做出了误判.采用小区域滤波技术可以完美的去除二值图中的误判标签.从最终的决策图可以看出，不仅聚焦图中的所有像素都进行了准确的分类，而且在聚焦区域和离焦区域之间获得了精准的分割边界.

表2 不同图像融合方法在Lytro数据集的客观度量结果

表3 不同图像融合方法对整个数据集的客观度量结果

图8 部分多聚焦图像的中间融合结果

对于两幅以上的多聚焦源图像进行融合，提出的方法同样是适用的.展示提出的方法对于两幅以上的多聚焦源图像的融合问题，采用Lytro数据集中的三幅源图像进行实验.三幅多聚焦源图像和最终的融合图像如图9所示.从图9中可以看出，在没有引入伪影的前提下，所有源图像中的聚焦区域都集成到了最终的融合图像当中.

图9 三幅多聚焦源图像的融合

2.2.4 参数讨论

对于窗口尺寸的问题，选择常用的滑动窗口尺寸4*4、8*8、16*16和32*32进行实验.当窗口尺寸为4*4和8*8时，由于活跃窗口包含的信息较少，所以在聚焦图中存在大量的标签误选.反之，当窗口尺寸为32*32时，虽然活跃窗口包含的信息更加丰富，有助于提高聚焦图中预测标签的准确率，但是较大的窗口容易导致聚焦区域之间的分割边界不精确.只有当窗口尺寸为16*16时，聚焦区域之间的分割边界才很精确.此时，虽然在聚焦区域内仍然存在少量的误选标签，但是这些误判的标签可以通过小区域滤波进行去除.对于整个数据集，不同窗口尺寸的实验结果如表4所示.从表4可以看出，当窗口尺寸为16*16时，提出的方法获得的融合效果是最好的.

表4 不同窗口尺寸的实验结果

对于二值分割的阈值问题，选取主要的分割阈值0、0.25、0.5、0.75和1进行实验.当分割阈值为0.25或者0.75时，与分割阈值0.5相比，不仅聚焦区域之间的分割边界不精确，而且聚焦区域内存在更多的误判标签.当分割阈值为0或者1时，与分割阈值0.25或0.75相比，获得聚焦图的实验结果更差.对于整个数据集，不同分割阈值的实验结果如表5所示.从表5可以看出，当分割阈值为0.5时，提出的方法可以获得最好的融合效果.

表5 不同分割阈值的实验结果

3 结 论

在本文中，利用拉普拉斯能量和卷积神经网络的多聚焦图像融合方法被提出来.该方法的新颖之处在于拉普拉斯能量算子可以有效的提取源图像中的聚焦信息，并且训练后的CNN模型根据提取的聚焦信息可以准确的区分清晰子块和模糊子块.清晰子块和模糊子块的聚焦特征完全不同，并且训练后的CNN模型具有很好的分类能力.在经过大量的样本训练后，对于给定的多聚焦源图像对，提出的方法可以产生精确度很高的聚焦图.在经过二值分割和小区域滤波后获得精准的决策图.根据最终的融合图像可以看出，提出的方法不仅精确的提取了源图像中的聚焦区域，而且获得了精确的分割边界.实验结果表明无论从融合图像的视觉效果还是从客观评价指标来看，提出的方法均优于已有的其它融合方法.在未来，深度学习的方法会进一步促进多聚焦图像融合技术的发展.