基于模糊神经网络的路桥工程建设项目应急能力评价

涂 晶， 李 伟， 陈欣悦， 庞奇志

(中国地质大学(武汉)工程学院,武汉 430074)

随着城市交通网络的迅速发展,路桥工程建设项目越来越多,路桥工程事故也时有发生,路桥工程建设具有施工现场多、工序繁多、施工技术复杂等特点[1-2],一旦发生事故,可能造成大面积伤亡,并会对周边地区造成较大的影响。因此,在路桥工程建设阶段,工程项目的应急能力需要重点关注,有必要对其应急能力进行评价,以便能及时发现应急能力建设的薄弱环节,采取有效措施加强应急能力的建设,预防事故的发生。

应急能力评价是一个复杂的系统过程,中国学者针对应急能力的评价方法进行了大量的研究。马茂东等[3]利用模糊综合评判法进行应急能力的评价,但是模糊综合评判法对隶属函数、隶属度的确定依然具有很大的主观性,且缺乏对环境的自适应能力,导致评估结果不够准确；尹俊淞[4]、葛悦等[5]借助灰色理论建立应急能力评估模型,然而灰色理论对数据的要求高,当数据离散度较大时,还必须借助统计分析技术进行相关处理；李树刚等[6]借助BP神经网路建立煤矿应急能力评估模型,结果显示其具有良好的实用效果,但是传统的BP神经网络为“黑盒模型”,可解释能力较弱。

前人研究为路桥工程建设项目应急能力评价提供了理论和实践基础,然而目前路桥工程应急能力评价领域尚欠缺体系性。基于此，首先建立科学的评价指标体系,并将模糊数学理论、层次分析法、BP神经网络相结合建立基于模糊神经网络的应急能力评价模型,最后通过实地调研和对比分析对模型进行验证。

1 应急能力评价指标体系

目前路桥工程建设项目应急能力评价领域还欠缺体系性,为建立科学完善的评价体系,本文根据公共价值导向原则、预警与预防为主的原则、弹性化原则等设计指标体系,采用专家调查法、问卷调查法和文献法,结合《突发事件应对法》等法律法规,建立并完善了如图1的应急能力评估指标体系。该体系分为两层,其中包含4个一级指标以及相应的15个二级指标。一级指标划分如下:预防与应急准备、监测与预警、应急处置与救援、事后恢复与重建；对应二级指标划分如下:预防与应急准备阶段分为制度、标准与办法,危险识别评估与风险减缓控制,应急资源保障系统,应急预案与宣传培训演练；监测与预警阶段分为应急信息监测,应急信息报送,突发事件预警；应急处置与救援阶段分为指挥协调,检测评估,抢险救援,信息发布；事后恢复与重建阶段分为善后处置,事故调查,表彰惩罚,恢复重建。

2 应急能力评价模型的建立

由于应急能力评价指标具有较强的模糊性,采用模糊系统和BP神经网络系统相结合构建模糊神经网络评价模型(图2)。模糊系统与BP神经网络系统具有多种结合方式,该模型采用串联的方式将模糊系统和神经网络结合起来,经模糊系统处理后

图1 路桥工程建设项目应急能力评价指标体系Fig.1 The evaluation index systern of emergency capability for road and bridge construction projects

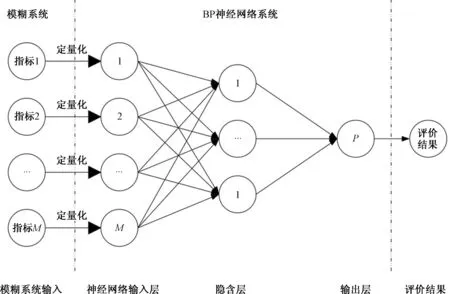
图2 模糊神经网络评价模型Fig.2 The fuzzy neural network evaluation model

的数据直接输出给神经网络系统[7]。第1层为模糊系统输入,它的每一个节点表示一个二级评估指标定性评价结果,当前层作用是将定性指标结果定量化并传给神经网络；第2层为神经网络输入层,节点数与二级指标数相同,每一个节点表示指标定量化后的数值；第3层为隐含层,可以完成神经网络输入值到输出值之间的映射；第4层为输出层,其输出即是神经网路输出结果[8]；第5层为评价结果。当不需要反归一化处理时,第4层输出层结果即为第5层评价结果。

2.1 模糊系统

应急能力评价指标具有模糊性,而BP神经网络是一种处理定量数据的方法[9],因此先将得到的定性评价结果交由模糊系统处理。模糊系统的作用是对定性的评价指标进行模糊处理,确定指标权重、指标状态集及其对应分值,计算二级指标得分和期望结果。具体操作方法如下:

(1)指标赋权。指标在各自层级中对评价结果的影响程度不同,因此采用层析分析法确定每个评价指标的权重[10]。使用Saaty 1～9标度法来对决策判断定量化,以形成数值判断矩阵,并对矩阵进行一致性检验,以此剔除无效数据,保证数据的有效性[11]。

(2)构造指标状态集V。根据Saaty 1～9标度法确定不同状态相应分值,即V={v1(n1),v2(n2),…,vm(nm)},vi表示指标状态,ni表示分值。

(3)计算各二级指标得分。细化二级指标调研问卷,采用专家打分法对二级指标进行评价,根据指标状态集确定相应得分,并以平均分作为各二级指标的最终得分。各二级指标的最终得分即为 BP 神经网络的输入值。

(4)计算期望结果。进行模糊综合评价,根据指标权重和各二级指标得分,计算最终应急能力评价得分。此评价得分结果作为期望结果。

2.2 BP神经网络系统

在应急能力评价过程中,指标体系往往比较复杂,指标间相互影响且模糊性较强,导致模糊综合评价法效果不够理想。基于BP误差反向传播算法的神经网络具有从输入到输出的高度非线性化映射的特点,与应急能力多指标评价适应性良好[12]。BP神经网络的信号传播主要分为输入信号的前向传播和误差信号的反向传播两个过程[6]。以四层BP神经网络(即含有两层隐含层)为例,假设输入神经元数目为M,其中任意一个用m标记；第1隐含层记为I,包含I个神经元,其中任意一个用i标记；第2隐含层记为J,包含J个神经元,其中任意一个用j标记；输出神经元数目为P,其中任意一个用p标记。其具体算法如下。

(2)样本数据经模糊系统处理得到训练数据集X,其中任意一个训练数据x为M维矢量；对应的期望输出集Y,其中任意一个训练数据y为P维矢量,将训练数据集X与对应的期望输出集Y同时输入到网络进行训练。

(3)计算各层的输入值和输出值。网络中输入信号以前向的方式传递,当前神经元的输出同时作为下层连接神经元的输入。神经元的输入记为u,输出记为v,用上标表示神经元所处层,下标表示当前层中序号,权重用w表示,如wij表示I层神经元传递到J层神经元的权重值。将模糊系统的输出作为整个神经网络的输入信号。

神经网络输入层的输入:

uM=xm

(1)

第1隐含层第i个神经元的输入:

(2)

第1隐含层第i个神经元的输出:

(3)

第2隐含层第j个神经元的输出:

(4)

输出层第p个神经元的输入:

(5)

输出层第p个神经元的输出:

(6)

输出层f(·)为输出函数,通常使用purelin线性函数。隐含层f(·)为传递函数,通常使用Sigmoid函数:

(7)

(4)误差E(n) 。输出层第p个神经元的输出误差:

ep(n)=dp(n)-yp

(8)

式(8)中：n为迭代次数,dp(n)为此神经元的实际输出。

(9)

若E(n) 小于期望的误差值,则训练结束,否则网络转向误差信号的反向传播,调整各层权值。

(5)各层权值修正。误差信号与输入信号相反,从后往前传播,在反向传播过程中,逐层修改权值w和权值修正量Δw,网络中学习效率记为η,当前神经元局部梯度记为δ。即为

w(n+1)=w(n)+Δw(n)

(10)

隐含层J与输出层P之间的权值修正量:

(11)

输入层M与隐含层I之间的权值修正量:

(12)

隐含层I与隐含层J之间的权值修正量:

(13)

权值调整结束后,网络继续由输入信号前向传播,直到最终误差达到要求,训练结束。

3 实例分析

3.1 模糊系统处理数据

通过对某区域5家路桥工程建设公司进行调研,邀请公司应急管理专家对其公司应急能力进行打分作为评价样本,填写AHP调研表。依据如图1所示的应急能力评价指标体系和AHP调研表,对各评价指标重要性两两比较,依靠层次分析法建立评价指标相对权重系数得到层次总排序结果如表1所示。并建立指标状态集V,将应急能力评价系统中的状态分为5个级别,即完全满足(9分),比较满足(7分),一般满足(5分),比较不满足(3分),完全不满足(1分),指标状态对应其得分情况。

3.2 确定神经网络结构

输入节点以图1指标体系各评价结果为基准,即将15个评价指标定量化的结果作为BP网络输入节点。最终评价结果为工程项目总体应急能力,因此输出节点数目为1,模型隐含层节点数目确定为8。因此本模型神经网络结构为15-8-1。

3.3 模型训练

BP网络结构设计完成后,设定学习效率为0.05,传递函数采用Sigmoid函数,输出函数为purelin函数,训练函数为trainlm函数,并随机初始化全部网络的权重和神经元的阈值。将经过模糊系统处理的专家库50组数据放入模型训练,经过5次迭代后,全局误差已满足设置要求。其训练结果如图3所示。

3.4 评价结果

将训练好的神经网络模型存储为可使用的函数,并对调研对象进行评价,其评价结果与模糊综合评价结果对比如表2所示。

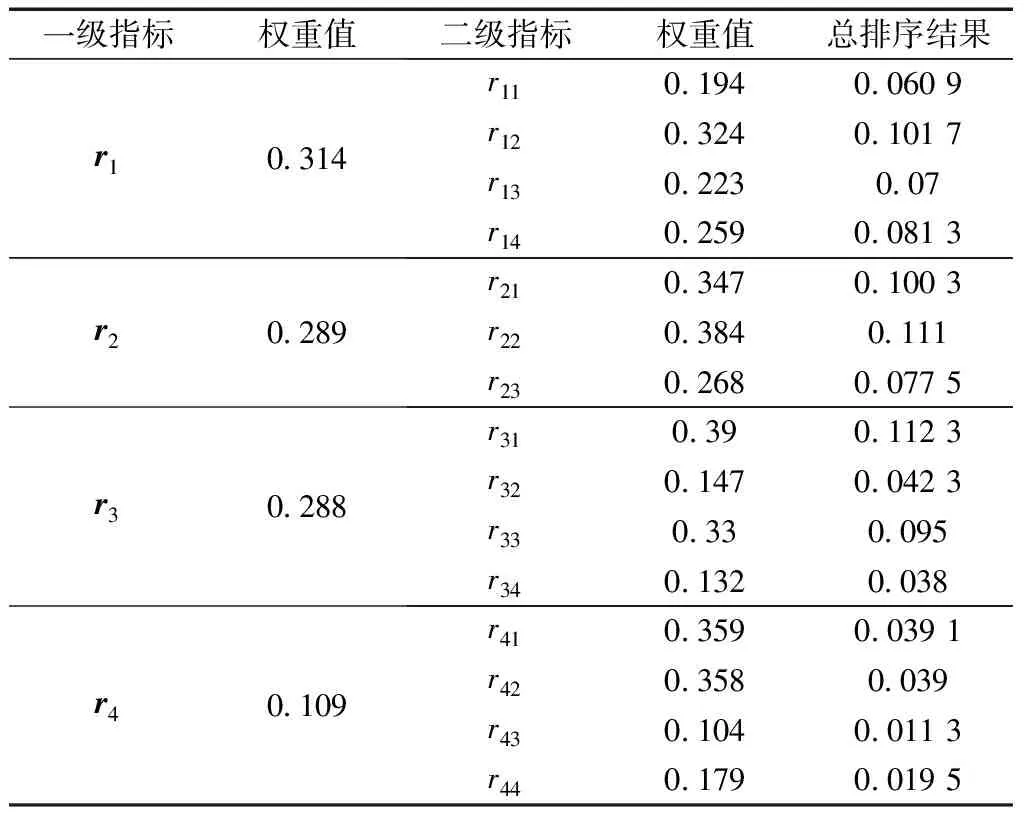
表1 应急能力评价指标权重(层次总排序)Table 1 Emergency capability evaluation index weight (overall ranking levels)

表2 两种方法评价结果对比Table 2 Comparison of evaluation results of two methods

图3 训练误差曲线Fig.3 Training error curve

通过对比模糊神经网络与模糊综合评价的评价结果,并以两种方法的评价结果差值绝对值作为误差,各评价结果误差如表2所示,且累计平均误差仅为2.02%,说明该模型精度较高,充分说明了所建立的模糊神经网络模型可以满足路桥工程应急能力评价的要求。

4 结论

考虑到路桥工程领域尚欠缺应急能力评价体系,使用多种方法相结合,提出了较为合理的应急能力评价指标体系,其指标体系包括4个一级指标和15个二级指标。在此基础上,建立了基于模糊神经网络的路桥工程建设项目应急能力评价模型,该模型随机初始化权重,由其自适应功能进行调整,避免了人为因素的影响。并将该模型应用于5家路桥工程建设公司,实际结果表明,该模型相比模糊综合评价法误差极小,且收敛速度快、操作简单,克服了模糊综合评价法计算复杂、权重确定主观性强且效率低的缺点。有针对性地将科学原理与技术运用到路桥工程建设项目应急能力评价领域,提出的模型精度高、人为因素影响小、操作简单,为路桥工程建设项目应急能力评价提供了参考。