基于粗糙集-模糊C均值聚类的Elman神经网络农村需水量预测

2020-02-24吴佳懋

科学技术与工程 2020年1期

李伟，李艳，吴佳懋

(海南大学土木建筑工程学院, 海口 570100)

精准的用水量预测是城乡供水一体化体系中一项重要的基础工作[1]。目前,中国推进从需求侧作为出发点研究水资源调配,需水量预测便成为学者研究重点。准确预测下一时间节点用户用水量不但对水力系统规划和提高经济效益有积极作用,也是中国水资源需求侧管理需要实现的重要目标。农村用水量由于其影响因子众多且影响程度不均,预测方法及改进手段的选择直接决定了预测的精准程度。

农村用水量预测的方法很多。赵伟国[2]按四平农村地区分析计算未来需水量,然后分析其未来水的供求态势；朱连勇等[3]建立了阿拉尔垦区需水量预测模型,在选取农业用水灌溉定额、工业用水重复利用率、城镇生活人均日需水量、农村生活人均日需水量作为模型输入,农业、工业、城镇生活、农村生活需水量作为输出的基础上利用 RBF 神经网络,将2001—2007年用水量数据作为训练样本,用2008—2009年用水量数据对模型进行检验,结果表明 RBF 神经网络模型用于该区需水量预测是可行的；李小建等[4]通过问卷调查获得第一手资料,根据生活用水量、畜禽饲养用水量、企业用水量、管网漏失和未预见水量4项指标建立农村用水量预测综合模型,并在软件ARCGIS 9.0中实现此模型,分析了镇平县农村需水量和缺水严重程度的空间差异及其原因。这些方法在一定程度上提升了农村用水量预测的精度,但在提取关键影响因素时,直接对备选因子进行取舍或者直接将因子综合出新的因子,忽略了影响因子单一影响和组合影响对于预测的重要性。

现以农村各个村落为研究对象,对农村各村进行用水量预测,为城乡供水管网规模确定、城乡水资源调度、和农村管网漏损的自动监测提供数据支撑。系统的介绍粗糙集-模糊C均值聚类Elman神经网络算法模型,且采用粗糙集-模糊C聚类 Elman神经网络模型对保亭县保城镇周边农村各村年用水量进行预测,最后进行误差计算并与 Elman神经网络预测结果对比验证预测模型的有效性。

1 模糊C均值聚类

模糊C均值(FCM)是一种软聚类方法,允许一条数据属于两个或多个聚类,主要是用隶属度去将数据点分类,隶属度越大代表数据点和聚类中心的距离越近。FCM基于以下目标函数的最小化:

(1)

式(1)中:m是大于1的实数;uij是在聚类J中的xi的隶属度;xi是D维测量数据的第i个数据;Cj是D维的聚类中心;dij=|xi-cj|是第i个聚类中心与第j个数据点之间的欧几里得距离。

模糊划分是对上述目标函数的迭代优化进行的,通过式(2)更新成员关系uij和集群中心cj:

(2)

Step1 用值在[0,1]的随机数初始化隶属度矩阵U。

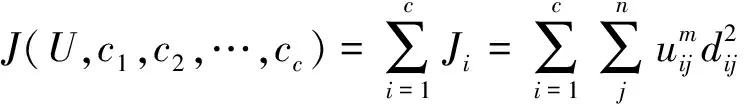
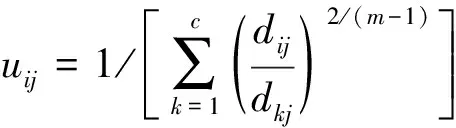
2 Elman神经网络和粗糙集理论

人工神经网络 (artificial neural network, ANN) 是一种模拟人脑神经系统信息处理机制的网络系统,是由现代神经生物学研究的基础上发展起来的。既具有处理数据的一般计算能力,又具有处理知识的逻辑思维、学习和记忆能力。Elman神经网络是一种递归神经网络,因其在隐藏层中增加了承接层作为延时算子而使系统具有了适应时变特性。

因为Elman神经网络的无限逼近作用,其在预测分析中被广泛应用,然而在数据量巨大和影响因子众多的情况下,模型的泛化能力会被降低,并且Elman神经网络在峰值点的预测结果偏差较大,因此引入粗糙集理论对Elman神经网络模型进行修正。

粗糙集理论是继概率论、模糊集、证据理论之后的又一个处理不确定性的数学工具，是当前国际上人工智能理论及其应用领域中的研究热点之一。粗糙集的特点是:①能处理各类数据,包括缺失的数据以及带有很多变量的数据；②能处理数据的不精确性和模棱两可,包括确定性和非确定性的情况；③能求得知识的最小表达和知识的各种不同层次；④能从数据中剥离出概念简单,易于操作的模式；⑤能产生精确而又易于检查和证实的规则。

粗糙集理论的核心思想就是对数据进行有效的分类并提取出对决策有关的“有用”数据。具体实现过程如下:

以Elman神经网络模型输出的预测值为基础,根据式(3)～式(5)提取条件属性集C={a,b,c},根据专家经验确定决策属性集D={d},从而构成完整的信息系统。然后分别对属性集C和D进行等频划分离散化处理得到决策表,采用粗糙集属性约简算法对决策表进行处理即可得到最小决策规则,从而确定尺度因子S,实现粗糙集对Elman神经网络模型的修正。

(3)

b=sgn(kt+1-kt)

(4)

(5)

式中:kt+1、kt分别表示预测函数在t+1时刻两侧的斜率；Yt为t时间单位内预测值；Y″t为t时间单位内实际值；M为数据点总数。

3 粗糙集-模糊C均值聚类Elman神经网络

将模糊C聚类理论和Elman神经网络结合,考虑农村用水量数据影响因子众多和影响程度不均的特性,首先按隶属度将数据点进行模糊C均值聚类,并用主成因分析法综合出若干影响因子,把综合出的影响因子并入原有影响因子构成影响因子组,再分别与每类村落用水量数据进行相关性分析提取关键因素,最后分别将每类村落预处理的用水数据和关键影响因素作为 Elman 神经网络的输入进行训练并预测,最后为了克服 Elman 神经网络在逼近非线性函数时,两侧斜率过大的峰值点预测误差较大,引入粗糙集进行修正,提高预测精度。

如图1所示,粗糙集-模糊C均值聚类Elman神经网络预测详细步骤如下:

(1)数据预处理。

(2)提取模糊C均值聚类的特征向量。

(3)设置参数并进行模糊C均值聚类。

(4)主成因分析综合出新的成分并与原始影响因子构成影响因子组。

(5)分别与每类数据进行 Pearson 相关性分析提取每类关键影响因素。

(6)数据归一化,将每类数据与其关键影响因素调整到0～1,这一步骤可确保 Elman 神经网络顺利进行。

(7)Elman 神经网络预测,将归一化的数据作为输入,设置训练目标最小误差、训练次数、现实频率和学习速率,在输出结果后可调整神经元个数以达到最优效果。

(8)预测结果反归一化并输出。

(9)将输出的预测值来构建条件属性集,根据专家经验选出的尺度因子构建决策属性集,通过等频划分的离散方法对集合进行离散化处理形成决策表,通过最小决策规则确定尺度因子,进行预测值修正。

4 案例分析

4.1 数据收集

选取海南省保亭黎族苗族自治县保亭县周边16个村落2010—2017年共8年用水数据进行预测。

4.2 模糊C均值聚类

图2所示为2010—2017 年村落年用水总量,可以看出每个村落的用水量趋势变化,并且村落与村落之间的规模差异较大。若将 16 个村落一起进行预测,必定会降低模型的泛化能力。因此,在进行预测之前首先要对村落进行分类。

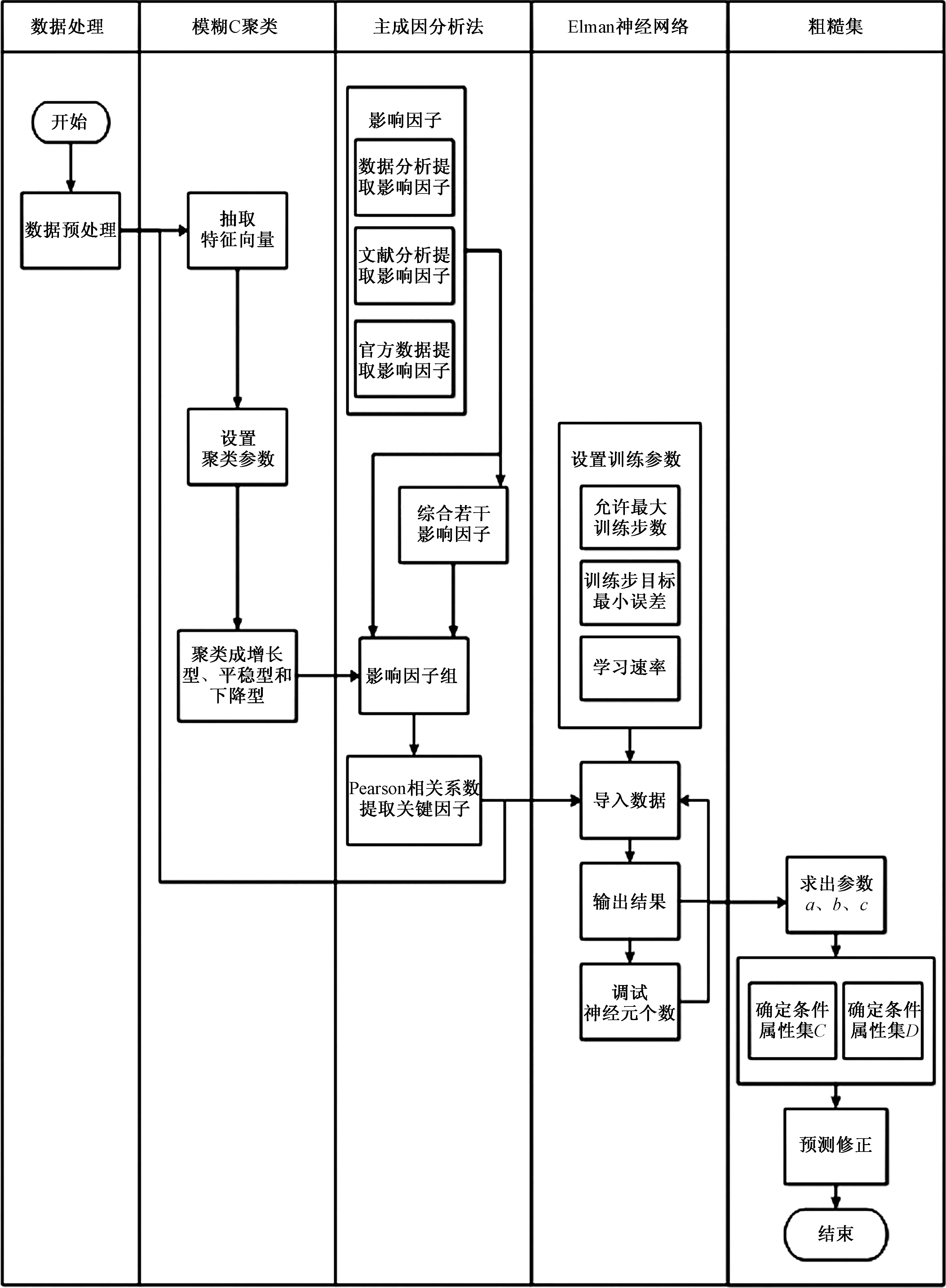
图1 算法流程图Fig.1 The algorithm flow chart

图2 村落年用水量汇总Fig.2 Summary of annual water consumption in villages

基于村落年用水量特性,提取村落年用水均量、村落年用水均方差和村中有效均户数作为聚类特征向量。村落年用水均量是可以体现出村落规模,反映数据集中趋势和一般情况的指标。年用水量的波动情况很大程度上影响了用水总量,村落年用水均方差反映了数据集的离散程度即波动的程度。村中有效均户数,即每个村平均每年真正使用水的用户数量。

表1为聚类特征的向量表,将聚类特征向量表作为模糊C均值聚类的输入。

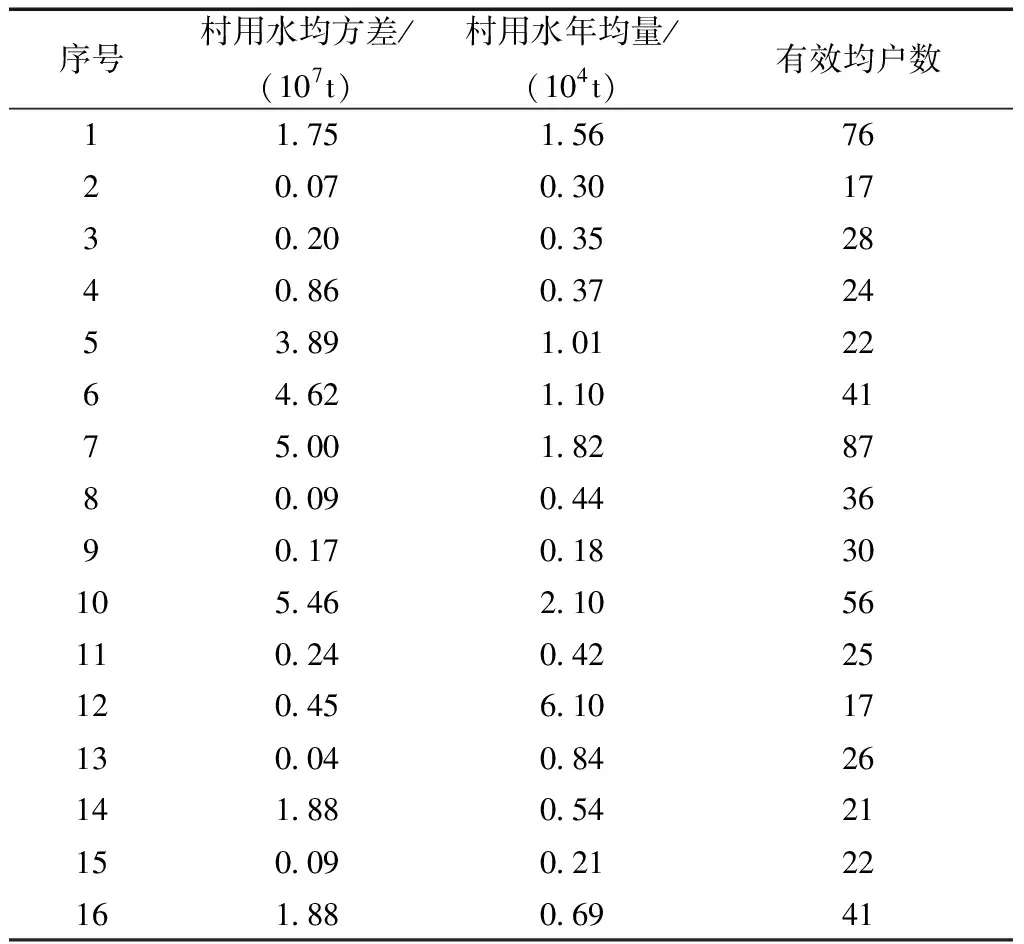
表1 聚类特征向量Table 1 Cluster feature vectors

根据表2所示设置参数,最后得出模糊C均值聚类的聚类数据图如图3所示。按照设定,将数据分为三类,中心黑色的点为聚类中心。

表2 聚类参数设置Table 2 Cluster parameter setting

图3 数据聚类图Fig.3 Data clustering diagram

根据模糊C均值聚类分类得出聚类结果如图4所示。第一类有5个村落,分别为村1、村5、村6、村7、村10；第二类有三个村落,分别为村4、村14、村16；第三类有8个村落,分别是村2、村3、村8、村9、村11、村12、村13、村15。

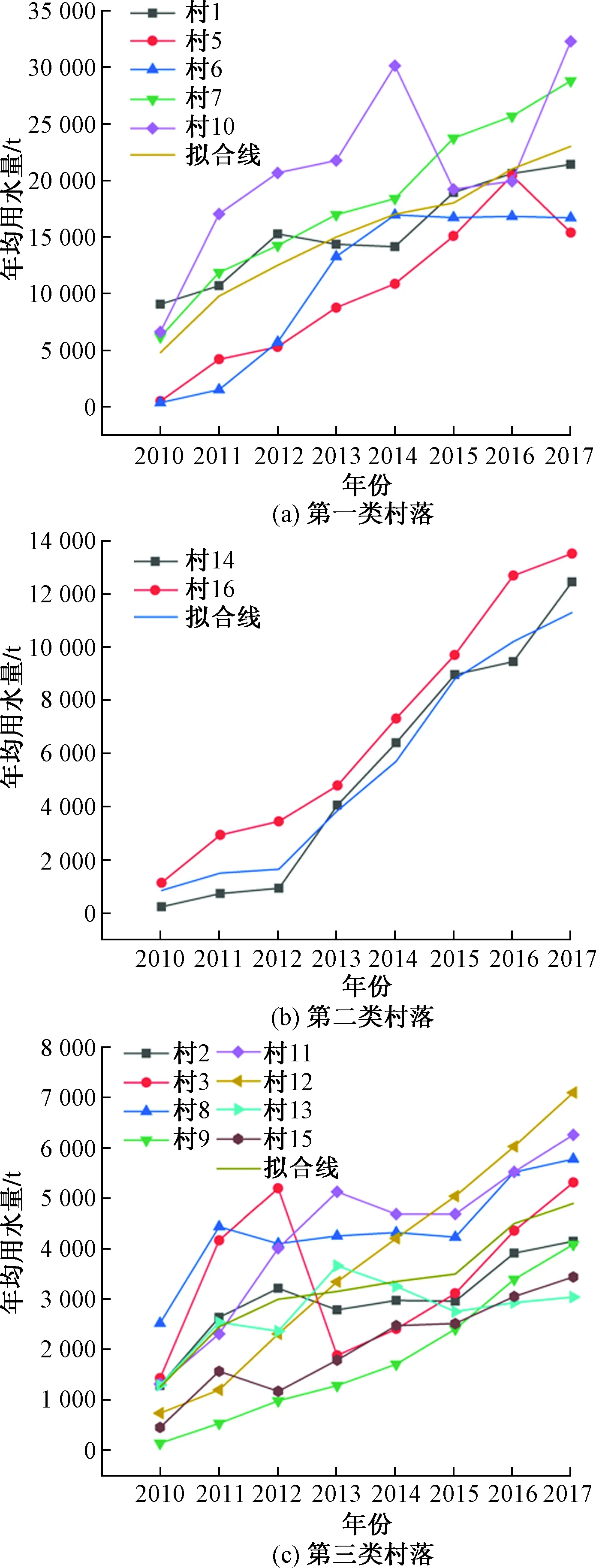
图4 村落聚类结果Fig.4 The results village clustering

图4和图5分别从二维和三维图上展现了模糊C均值聚类的分类结果。图4(a)所示为第一类村落,特点为用水量跨度大,波动较大；图4(b)所示为第二类村落,其增长速度稍放缓,但用水量跨度仍在[0,14 000]；图4(c)所示为第三类村落,增长趋势最平缓。由图5可知,从左边的第一类到右边的第三类,随着时间的增长,增长幅度趋近平缓,波动减小。

图5 分类结果三维对比Fig.5 Classification of three-dimensional comparison

4.3 关键影响因素提取

4.3.1 数据分析提取影响因素

经过数据分析、相关文献[5-14]分析以及官方数据分析提取农村用水量影响因素如表3所示。

表3 影响因素汇总Table 3 Summary of influencing factors

4.3.2 影响因子降维处理

农村用水量是多影响因素的复杂系统,在用水量预测研究中,多影响因子作为变量是普遍存在的,在经过影响因子的提取后得到了大量可能影响农村用水量的影响因子。但是,影响因子过多,无疑会增加预测的难度和复杂性。为了克服直接进行相关性分析对影响因子的筛选造成忽略其余影响因子对村年用水量的影响,采用主成因分析法综合出若干影响因子,所得出的影响因子和原有的影响因子作为最终的影响因子组。主成因分析法具有可消除评价指标之间的相关影响、可减少指标选择的工作量的优点。除此之外,主成因分析法反映了该主成分包含原始数据的信息量占全部信息量的比重,克服了某些评价方法中认为确定权数的缺陷。

应用 IBM SPSS 软件实现对新影响因素的提取,主成因分析结果提取两个成分如下:

(6)

式(6)中:yt(t=1,2)为提取的成分,具体值由成分系数表确定；ai(i=1,2,…,10)为主成分方差贡献率,ai越大表示主成分反映综合信息的能力越好,可以根据其大小来提取主成分,xi为原有的10个影响因子。

将影响因子组的12个影响因子分别与三类村年用水数据中的拟合线进行Pearson相关性分析,相关性系数如表4所示。

表4 相关性矩阵表Table 4 Correlation matrix

综上分析,根据相关系数逆序排列,选取每类前4个为提取的关键影响因子，如表5所示。

表5 关键因素提取Table 5 Extraction of key factors

4.4 Elman神经网络

将提取的关键影响因素与该类村2010—2016年用水量数据作为输入,算法训练采用前两年训练,随后一年的数据作为训练检验,以此类推,最后采用2015 年和 2016 年的数据作为预测基础,对 2017 年村用水量进行预测。预测前将 Elman 神经网络参数设定如表6所示。

表6 算法的参数设置Table 6 Parameter setting of the algorithm

在预测中,隐含层神经元对结果的影响也很大。根据经验,神经元个数的选择应遵循经验公式n=2t+1进行选择,其中t为Elman神经网络输入的维度,经调试后依最好的结果最终选定隐含层的神经元个数为80。

4.5 粗糙集修正

神经网络具有无限逼近的能力,在逼近非线性函数时,两侧斜率过大的峰值点预测误差较大。村与村之间年用水量差异性大,易产生波动,Elman 神经网络进行预测时峰值点会呈现不同程度的预测偏差,引入粗糙集对预测出的用水量序列进行修正,提高预测精度。

根据表7所示的条件属性和表8所示的决策属性,采用最小决策规则确定尺度因子,对预测值进行修正。

表7 条件属性Table 7 Conditional attributes

表8 决策属性Table 8 Decision attributes

4.6 仿真结果对比

使用MATLAB软件实现粗糙集-模糊C均值聚类Elman神经网络预测模型并与Elman神经网络模型的预测结果进行对比分析。经粗糙集-模糊C均值聚类Elman神经网络预测,每类村庄的用水量分别得出的预测结果如图6所示。

图6 粗糙集-模糊C均值聚类Elman神经网络预测结果及误差Fig.6 Prediction results and errors of Elman neural network based on rough fet-fuzzy C-means clustering

图7 算法预测结果对比Fig.7 Comparison in prediction results of the algorithms

图6和图7为Elman神经网络、粗糙集-模糊C均值聚类Elman神经网络预测相同16个点即16个村庄年用水量预测。由图7可以看出Elman神经网络、粗糙集-模糊C均值聚类Elman神经网络两个模型的预测趋势大体是一致的,但突然增大或减小时,Elman神经网络预测结果的变化幅度较小；从图7的误差分析可以看出,经粗糙集-模糊C均值聚类改进效果明显,误差范围从[0,0.6]缩小到[0,0.3]。

4.7 误差分析

为更加准确地量化比较两个模型的有效性,引入3个国际上使用较多的误差指标: 平均绝对百分比误差(MAPE)、预测值与实际值之间的差值的绝对值的平均值(MAE)和 SMAP (MAPE的一个延伸指标)作为误差评价指标，其计算方式为

(7)

(8)

(9)

式中:Yt为观测值；Y′t为预测值;N为数据个数。计算结果如表9所示。

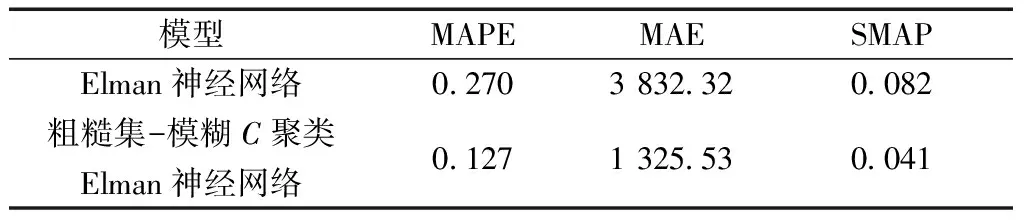
表9 误差对比分析Table 9 Comparative analysis of errors

经过误差计算,Elman 神经网络的MAPE为0.270,而粗糙集-模糊C均值聚类只有0.127,SMAP也从0.082降到了0.041,预测精度提高了一倍。绝对误差指标也从3 832.32减少到1 325.53,3个指标也同时验证粗糙集-模糊C聚类Elman 神经网络比单一Elman神经网络预测精度更高,优化模型有效。