基于健康指数相似的航空发动机剩余寿命预测
2020-02-24曹惠玲梁佳旺崔科璐
曹惠玲, 梁佳旺, 崔科璐
(中国民航大学大学航空工程学院学院,天津 300300)
航空发动机剩余寿命预测是发动机健康管理中的重要内容,合理的下发时间预测能够降低风险发生的概率,减少维修成本[1]。航空发动机结构复杂、工作环境恶劣,难以通过物理模型来描述其衰退过程[2]。目前依据大量状态监测数据的数据驱动方法是一种使用较为广泛的剩余寿命预测方法。厂家QAR详细记录了发动机每次飞行循环的多种状态参数,这些数据中隐含了反映发动机健康状态的信息[3]。与以往仅以EGTM(排气温度裕度)作为性能指标相比,综合发动机多源性能参数的健康指数能够更为准确的表征发动机当前性能衰退状况。在实际情况中,同一机型发动机不同个体之间存在出厂制造差异,在使用维护过程中也由于不同的维修等级、飞行环境等因素造成个体间衰退规律不同。所以如何体现个体差异性成为预测过程中需要面对的重要问题。在剩余寿命预测研究领域,基于相似性的预测方法能够较好的对比分析个体间的差异性。
基于相似性的预测方法已经在多个领域得到应用,如股票价格、医疗诊断、语音识别、轴承剩余寿命等,通过与大量历史样本发展趋势进行对比学习,能够取得良好的预测效果[4]。在航空发动机剩余寿命预测中,通过对比发动机退化序列之间的相似性,认为与服役样本具有相似退化模式的历史样本能够提供更有价值的参考。在大量历史数据样本下,通过对比样本之间时间序列相似性来预测系统剩余寿命,是一种能够很好地解决个体差异性的预测方法。李强将时间序列相似性匹配方法引入到地震预报中[5];Zhang等通过相似性寿命预测方法对NASA提供的C-MAPSS涡扇发动机仿真数据进行研究,预测结果远优于神经网络方法[6];任博等在欧几里得函数基础上通过引入衰退系数构建相似性函来预测风电机剩余寿命[7];申中杰等提出一种基于相对特征和多变量支持向量机的方法来预测机械设备轴承剩余寿命[8]。
目前通过对比衰退序列相似性来预测航空发动机剩余寿命的研究还比较少,关键问题之一就是难以找到足够的全周期衰退数据样本。针对Trent700发动机机队具有多源监测数据以及大量全寿命周期历史样本的特点,将多源性能参数通过状态空间模型融合为表征发动机退化状况的健康指数;通过聚类分析重构健康指数序列;对比测试发动机与历史发动机退化序列的相似度,赋予相似样本不同权重来预测发动机剩余寿命。
1 多源数据融合的健康指数
对于航空公司而言,导致发动机下发的主要原因包括:发动机性能衰退、时寿件到寿、叶片裂纹或烧蚀、某些参数超限等。在很多情况下,性能衰退是导致发动机下发的重要原因。对于因性能衰退导致下发的发动机而言,由于衰退程度无法直接测量,通常会比较实际与出厂EGTM来判定发动机衰退状态,这种方法简单易行,在航空公司得到了广泛应用。但EGTM阈值标准是根据使用经验制定的,设定太低会造成寿命件过度损耗,设定太高会浪费发动机剩余寿命;并且EGTM会受到季节温度变化、发动机水洗等因素影响,造成其短期变化较为明显,但这种变化并不代表发动机整体性能的变化[9-10]。发动机的多种状态参数能从不同的侧面表现其退化状况,所以对于发动机这样的复杂系统来说,融合多个状态参数的信息能够更为准确地反映系统状态。所以引入了发动机健康指数(engine health index,EHI)代替EGTM来表征发动机的健康状态。
1.1 性能参数选取
通过现阶段飞行监测系统得到航空发动机的多源监测数据,并且各类参数都是严格连续的,满足构成时间序列的需求,为数据融合提供了良好的数据基础[11]。为构建EHI,首先需要对多源监测数据进行相关分析,选取与发动机性能衰退相关性最强的几个性能参数来表征发动机健康状态。
相关分析常用方法包含协方差及协方差矩阵、图表相关分析、一元回归及多元回归、相关系数、信息熵及互信息五种。依据监测数据特点,选取相关系数法进行相关分析。相关系数是反应变量之间关系密切程度的统计指标,取值区间在1~-1之间。1与-1分别表示完全正相关或负相关,取值为0表示完全不相关,相关系数通常用表示。
(1)
式(1)中:sxy为样本协方差;sx和sy分别为样本和的标准差,计算公式如下:
(2)
(3)
(4)
通过统计分析软件SPSS对发动机飞行循环数与各性能参数分别进行相关性分析,选取相关性最强的五个性能参数EGTM(发动机排气温度)、ΔN3(高压转子转速偏差值)、ΔFF(燃油流量偏差值)、ΔP25(压气机2.5级压力偏差值)、ΔP30(压气机出口压力偏差值)融合为表征发动机衰退状态的健康指数EHI。
1.2 数据预处理
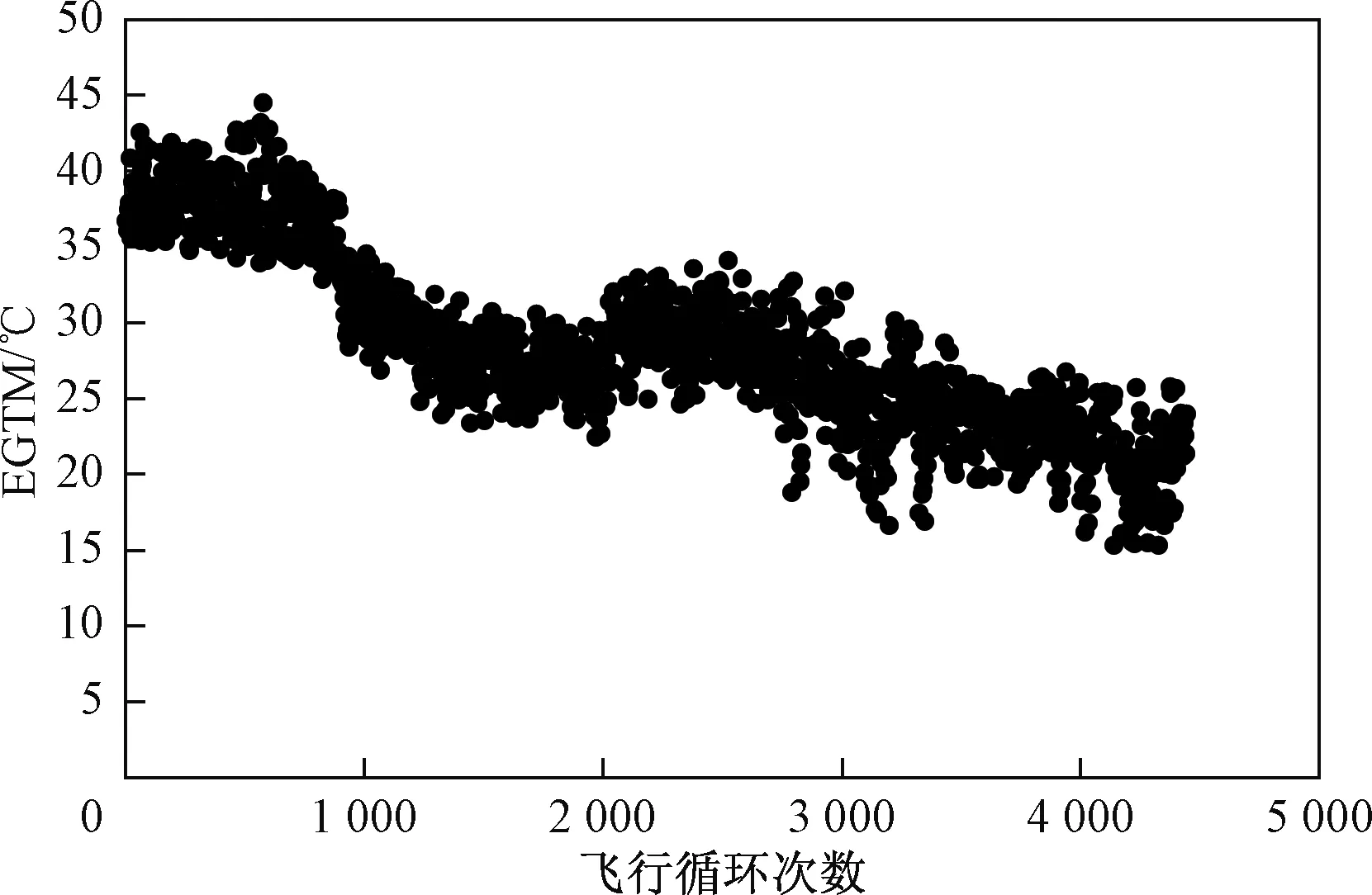
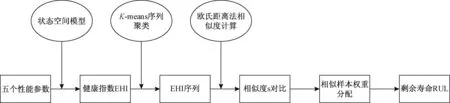
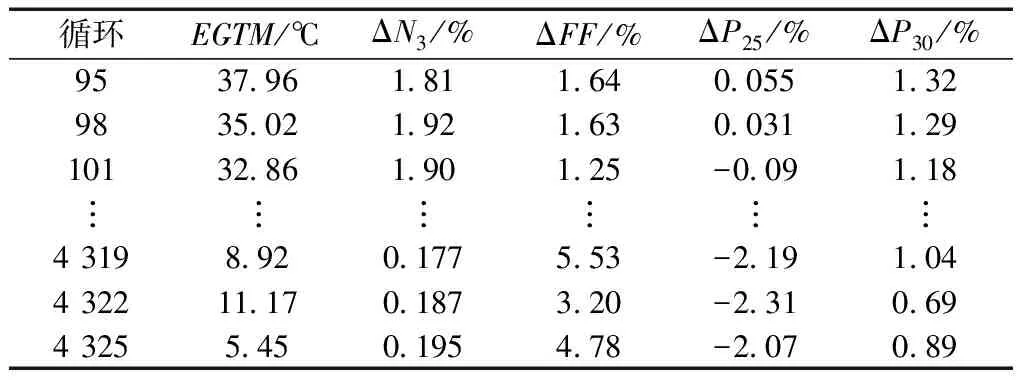
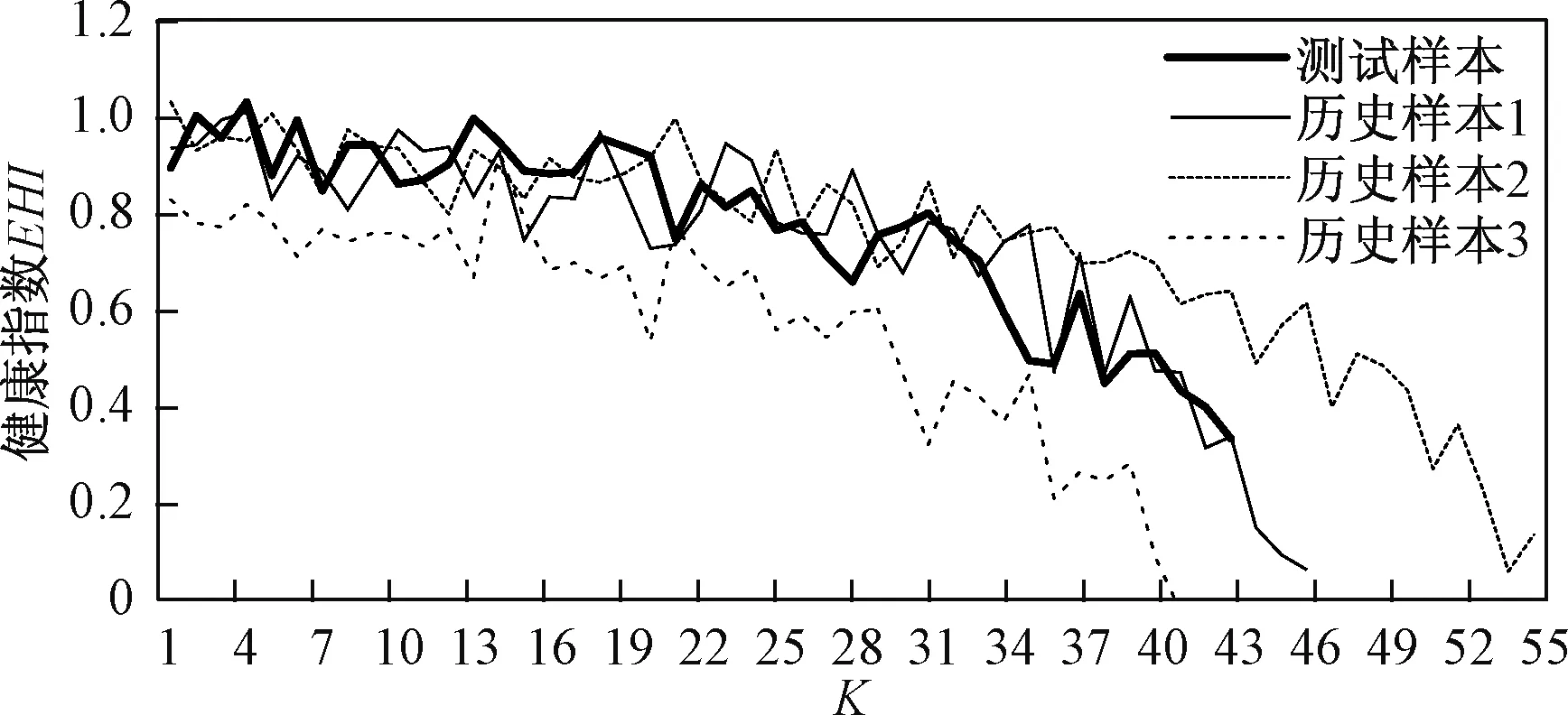
航空发动机在运行过程中,根据厂家所提供的面向客户的预警记录,发现少数时刻由于监测探头损伤,数据记录错误等因素影响,会造成监测数据出现异常值,为保证后续预测的准确度,需要对原始数据进行异常值筛选。选取狄克松(Dixon)判别法对异常值进行处理。狄克松判别法是一种用极差比双侧检验来剔除异常值的方法[12],根据数据量将数据序列分为若干区间,每个子区间可认为是独立同分布的。该准则采用极差比的方法,在每个子区间中,设样,根据其值的大小排序,假设x1 xn-xn-1>D-α(n) (5) x2-x1>D-α(n) (6) 式中:D-α(n)为Dixon所给的临界值,D为子区间数据统计检验量,α为显著水平,一般取0.05或0.01。若式(5)、式(6)成立,则说明xn、x1为异常值,应剔除,剔除后分别将xn-1与x2作为极大值和极小值继续比较。在双侧对比中如果对比结果小于D-α(n),则对比停止,该侧不再存在异常值。 图1中数据为机队中某台发动机EGTM原始监测数据,通过狄克松判别法剔除异常值后如图2所示,可以看到该方法比较有效地剔除了原始数据中的粗大误差值。 图1 EGTM随飞行循环变化趋势Fig.1 EGTM trend pattern with flight cycle 图2 去掉粗大误差后的EGTMFig.2 EGTM after removing the gross error 在得到与发动机性能衰退密切相关的五个性能参数后,利用状态空间模型对性能参数进行融合,人为地建立系统健康指数来表征发动机当前状态。 ZEHI=ft(x1,x2,…,xn) (7) (8) 式中,ZEHI为构建的发动机健康指数EHI,ZEHI=1代表发动机处于完全健康状态,ZEHI=0表发动机因性能衰退而下发;x1,x2,…,xn为发动机在t=1,2,…,m时不同的性能参数值;K为模型系数矩阵。在计算过程中选取机队中5台初始性能良好的新发全寿命周期数据作为训练样本,x1,x2,…,x5分别为1.2节中选取的五个性能参数,每台发动机前20个循环性能参数对应的健康指数为1,因性能衰退下发时刻前20个循环对应健康指数为0。得到模型系数矩阵K后将机队中每台发动机全周期数据代入,得到每台发动机的健康指数时间序列。 多种性能退化参数变量已被转化为表征航空发动机健康状态的单一指标量—EHI。健康指数与发动机飞行循环构成典型的一维时间序列,利用面向一维时间序列相似性对比的预测方法来预测服役样本的剩余寿命。QAR详尽地记录了每次飞行循环的监测数据,但对于同一性能参数,每次飞行循环之间由于飞行环境不同以及监测误差等因素影响造成相邻两点数据相差较大,这种短期波动对于着重于长期发展趋势的寿命预测研究来说没有太大参考价值,并且会在计算序列相似度时增加计算时间和计算误差,所以需要对健康指数时间序列进行聚类分析。 对于任意两个EHI时间序列之间的相似性度量应满足:对短期波动不敏感,但是能够有效地反映长期趋势。采用K-means聚类算法对EHI时序数据进行聚类分析。K-means算法也称为K-均值算法,是聚类分析中的一种经典算法,具有简单、快速、适合处理大数据集的特点[13]。预测流程框架如图3所示,具体计算过程如下: (1)给定总量为的数据集,令I=1,选取个初始聚类中心Zj(I)(j=1,2,…,k)。 (2)计算剩余的每个数据点与聚类中心之间的距离,D[xi,Zj(I)(i=1,2,…,n)],如果满足D[xi,Zj(I)]=min{[xi,Zj(I)],i=1,2,…,n}则xi∈ci。 (3) 计算k个新的聚类中心: (9) 即取聚类中所有元素各自维度的算数平均数。 (4)判断:若Zj(I+1)≠ZJ(I),则I=I+1,重复(2);否则结束。 其中准则函数定义如下: (10) 式(10)中,G为所有对象平方误差总和,p为数据对象,mi是簇Ci的平均值,准则函数使生成的结果尽可能紧凑独立。距离D计算通常使用欧式距离法: D(X,Y)= (11) 则函数J收敛时得到新的健康指数序列EHIoi(i=1,2,…,k)。 通过对EHI时序数据完成聚类分析后,采用时间序列相似性匹配方法进行寿命预测,也就是对比预测样本序列与历史样本序列之间衰退趋势的相似性,计算流程如下: 2.2.1 对比时间序列 相似度的算法通常有欧氏距离法、动态时间弯曲距离法(DTW)等[14-15],由于欧氏距离法具有普遍适用、计算速度快的特点,采用欧式距离法[16]计算相似度: (12) 即分别计算测试样本序列EHIoi与历史数据库中每个历史发动机样本EHIpi在0~k点序列段之间相似度,在EHIpi中p=1,2,…,m,代表历史数据库中的m个历史样本,j=1,2,…,k,…,n,代表每台历史样本序列点数。 2.2.2 样本权重分配 与预测样本衰退过程相似度最高的历史样本在剩余寿命预测时应享有最高的参考比重,所以预测前需要对相似的历史样本赋予相应的权重,在预测过程中选取历史样本库中相似度最高的台发动机作为参照样本。 (13) (14) 2.2.3 剩余寿命预测 L个样本在k点处对应的剩余寿命RULi为已知,赋予L个样本剩余寿命不同权重,可得到测试样本剩余寿命RUIo: (15) 图3 相似性剩余寿命预测模型框架Fig.3 Similarity residual life prediction model framework 在本文所研究的航空发动机剩余寿命预测问题中,使用的数据是航空公司QAR记录的发动机最大起飞推力下的监测数据。该数据为机队中Trent700系列发动机在不同飞行环境下的全寿命周期状态监测数据,部分数据如表1所示。 表1 部分监测数据Table 1 Partial monitoring data 数据库共包含28台因性能衰退导致下发的发动机全寿命周期状态监测数据,将其中23台作为历史样本,另外5台作为测试样本。在本文中,首先通过状态空间模型将所有样本与发动机性能衰退相关性最强的性能参数EGTM、ΔN3、ΔFF、ΔP25、ΔP30转化为能够表征发动机退化水平的健康指数,构成发动机性能衰退的一维时间序列;然后对健康指数序列进行聚类分析处理;最后计算测试样本序列与历史样本序列之间的相似度,依据样本间相似度大小配以不同参照权重来预测剩余寿命。 通过状态空间模型将多个性能参数融合为健康指数EHI来表征发动机当前健康状态。 根据1.3节中所给方法得到模型系数矩阵KT。 (16) ZEHI=-1.791+0.038x1+0.1434x2+0.273x3+0.119x4+0.2473x5 (17) 通过训练模型得到机队中每台发动机健康指数时间序列,图4所示为机队中某台发动机健康指数序列趋势图。可见,数据点并不是非常集中,究其原因认为,不同航班发动机起飞时大气环境存在较大差异;监测数据在测量记录过程中存在一定程度误差;某些性能参数值随自身性能的影响波动比较大;发动机在维修后性能恢复程度不同等等,这些因素均会导致发动机健康指数序列存在波动[17],而这种波动也恰好真实反映了发动机在使用过程中的实际情况。 图4 EHI随飞行循环变化趋势Fig.4 EHI trend pattern with flight cycle 通过健康指数表征的航空发动机性能退化过程是一种典型的一维时间序列。根据2.1节所给方法对序列进行聚类处理,根据计算得到:当类间距离取97时,既能得到很好的聚类效果,又能在相似度对比时具有较高准确度。利用欧氏距离法计算测试发动机序列与样本库历史发动机序列的相似度,图5为测试发动机与部分历史发动机衰退过程时间序列对比,历史样本1与测试样本具有较高的相似度,与历史样本2、历史样本3与测试样本相似度较低。 图5 EHI序列对比Fig.5 EHI sequence comparition 通过相似度计算选择与测试发动机相似度最高的5台历史发动机作为参照样本,依次按照相似度大小通过2.2节所给方法赋予这5台发动机不同权重值。根据2.3节所给方法在测试样本全寿命周期80%处进行预测,在序列相似性匹配过程中分别使用了EHI序列与EGTM序列,并与发动机的实际下发循环进行对比,预测结果对比如表2。 由上可见,通过将多源参数融合为健康指数构建的时间序列预测结果平均误差为4.6%,其中单台最大误差为6.4%,最小误差为2.8%;通过单参数EGTM构建的序列预测结果平均误差为7.9%,单台最大误差为9.3%,单台最小误差为7.2%。从 表2 预测结果Table 2 Forecast result 测试样本预测结果来看,通过EHI序列预测的误差都要小于通过EGTM序列预测的误差,这也表明了使用健康指数来表征发动机性能衰退状态的优越性。 基于相似性的预测方法适用于难以建立准确退化模型的复杂系统中。针对航空发动机退化模式具有较大个体差异性的特点将相似性寿命预测方法引入到航空发动机剩余寿命预测研究中。 (1) 通过状态空间模型将多源监测数据融合为健康指数,相比单性能参数来说健康指数能够更为准确地表征发动机衰退状态。 (2) 利用K-means聚类方法构建新的健康指数时间序列,可有效地缩短计算时间,提高相似性匹配准确度。 (3) 通过欧氏距离法计算样本之间相似度,根据相似度大小赋予历史样本不同参照权重,使寿命预测更为准确。 (4) 对比单参数与健康指数两种预测方法,结果证明后者具有更好的预测结果,同时能够给航空公司发动机维修决策制定提供可靠依据。
1.3 健康指数融合
2 基于相似理论的剩余寿命预测
2.1 时间序列聚类分析
2.2 序列相似度计算
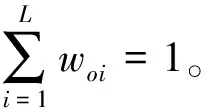
3 实例分析


4 结论
