油页岩气体热载体干馏炉炉内流动特性

2020-02-24华泽嘉蒋佳奇王智超

科学技术与工程 2020年1期

华泽嘉，王擎，蒋佳奇，王智超

(1.华北电力大学能源动力与机械工程学院,北京 102206；2.东北电力大学能源与动力工程学院,吉林 132012)

油页岩又称油母页岩,是一种以无机矿物质为骨架,内含固体有机质的沉积岩,作为固体化石燃料,与煤、石油、天然气一样均为不可再生化石能源。油页岩储存量丰富,具备作为传统化石燃料替代能源的巨大潜力和条件[1-3]。目前阶段中外油页岩提取燃料的处理方式主要有两种:分别应用固体热载体和气体热载体为热源的干馏炉干馏工艺。在油页岩气体热载体干馏工艺中,使用最为广泛的是固定床干馏工艺,如抚顺式干馏炉、佩特洛瑟克斯炉、鲁奇加压气化炉、苏联基维特炉等[4-5]。中国油页岩气体热载体干馏工艺以抚顺式干馏炉为主,该炉为筒形结构,半内燃、半循环式并使用蓄热式加热炉进行配合,热量交换主要以对流换热方式进行[6-8]。对气体热载体干馏炉而言,气体热载体在被送入干馏炉时的布气方式对油页岩干馏影响较大,总结现有的气体热载体干馏炉的布气方式,主要存在以下问题:气体热载体布气方式过于简单,使得气体热载体在炉内布气不均匀；气体热载体在干馏炉上的布气范围窄,使得油页岩在通过高温干馏段时受热时间短,油页岩没有完全干馏就离开干馏段,浪费资源。近几年,随着生产能力扩大,大直径固定床反应器的应用更加广泛,掌握固定床内流体的流场特性日趋重要。中外许多研究人员对固定床的流场进行了研究,并提出了相关的数学模型。Anthony等[9]利用CFD技术对固定床反应器床层低管径比结构进行了模拟,获得床层内包括速度、压力等更精确的信息；宁平等[10]通过实验及理论研究对固定床的边流效应做了相关研究,得出通过增大塔径与吸附剂的粒径比、增大固定床的长度、以及在固定床内部结构上设计等结论,可以减少壁面效应；秦宏等[11]基于Ergun方程对油页岩干馏炉的压力降进行计算,并与实际压降进行比较,所得理论值与实际值比较接近,且变化趋势与实际值基本一致；陈金娥等[12]采用多孔介质模型和统一流场等方法对大型轴向流固定床反应器内流场进行了数值模拟,得出模拟和计算结果均能合理地反映出固定床内部气体流动情况；Atmakidis等[13]对床层内壁面对流动性能的影响进行了分析,获得模拟过程中壁面处详细的速度及孔隙率的分布,得到壁面对流动影响的特点,从而对固定床结构进行优化设计。

现借助中外相关经验,采用计算流体力学(computational fluid dynamics, CFD)方法对一台1 t/d油页岩气体热载体干馏炉内流场特性进行三维稳态数值模拟。首先对数学模型进行研究,运用所建立的模型进行三维数值模拟,并对不同布气方式下干馏炉内流场特性进行详细研究,得到最优布气方式。这将对改进以往优化设计时凭借经验且带有盲目性的情况,具有一定工程实际意义。

1 物理模型

1.1 几何模型

基于实际的实验炉体进行研究,其结构如图1所示。炉体从上至下依次为进料段、干馏段和冷却段,在炉体进料段所在的炉体顶部设置料斗,炉体上部设有油气出口。在干馏段所在的炉体上设有密封的第一布气风箱及第二布气风箱,并设有与布气风箱连通的布气装置,在冷却段所在的炉体上设有密封的第三布气风箱及布气装置。布气装置为长520 mm、宽100 mm、高100 mm的方管形式,对称布置在炉墙两侧。干馏段布气装置上下均匀布置两个50 mm×50 mm的喷嘴,冷却段布气装置上下布有一个40 mm×40 mm的喷嘴。

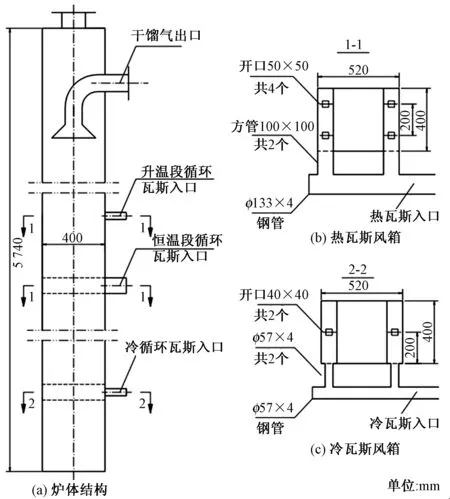
图1 模拟对象几何模型Fig.1 Geometry model of the simulation object

1.2 参数设置

入口采用速度入口边界条件,出口采用压力出口边界条件,固定床壁面处采用无滑移边界条件。气体的黏度和密度按常温下对应的值进行设定。具体参数及初始条件如表1所示。

表1 模拟对象主要参数Table 1 Main parameters of the simulation object

2 数学模型

2.1 控制方程

连续性方程:

(1)

动量方程:

(2)

式中:ρ为密度；Sm为源项；Si为阻力源项；τij为应力张量。

2.2 多孔介质模型

固定床层中的固体颗粒分布比较均匀,颗粒尺寸相比于固定床直径而言是非常小的,因此可以将固定床层内堆积的颗粒视为均匀各向同性的多孔介质。考虑到气体在多孔介质空隙中的流动情况非常复杂,且页岩颗粒的堆积状况并不规则,气体在多孔介质的各个空隙中的流动情况并不规律。因此,在工程实际中一般不讨论气体在多孔介质的每个微小空隙中的流动情况,对既包含大量固体颗粒和微小空隙但又比固定床直径小得多的微元体积中流体质点的流动状态进行平均,从而得到气体在多孔介质区域中的宏观流动规律。多孔介质模型非线性微分方程在均匀各向同性的多孔介质区域中,阻力源项表达式为[14]

(3)

式(3)中,1/η和C2分别为黏性阻力系数和惯性阻力系数,根据Ergun方程获得求解两系数的表达式为

(4)

(5)

式中:ε为多孔介质空隙率;dp为颗粒的当量直径;a=150；b=3.5。

2.3 湍流模型

在固定床内的流体由于受到固体颗粒阻力的影响,流动状态为层流。在固定床层上方的自由流动区域,流动状态为湍流,尤其在此区域内,气流中具有较大的回流和漩涡。因湍流控制方程的不封闭性,在研究湍流的发展过程中,形成了湍流模式理论,现采用该理论的涡黏模型中的双方程模型使方程封闭。目前,双方程模型在工程中使用最为广泛,最基本的双方程模型是由Launder和Spaldinig提出的标准k-ε模型[15],但该模型用于弯曲流线流动时,仍会产生一定的失真,为了弥补缺陷,许多研究者提出了对标准k-ε模型的改进方案,应用最广泛的是RNGk-ε模型和Realizablek-ε模型[16]。由于k-ε模型没有考虑各向异性湍流结构的影响,所以现采用的是Yakhot和Orszag提出的基于重整化群方法推导的RNGk-ε模型,该模型对湍流的动能耗散项进行了修正,增加了一个附加项,具体形式为[17]

(6)

(7)

(8)

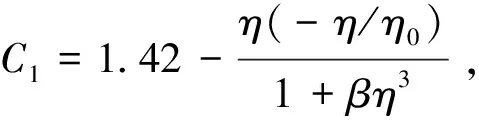
3 模型求解

采用Gambit建模软件对计算主体进行构建,网格划分采用六面体结构化网格。如表2所示,分别采用网格尺寸为10、12、18 mm的网格进行网格无关性验证。

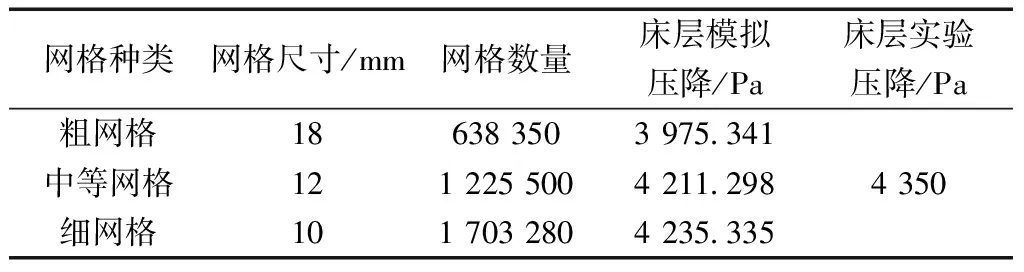
表2 不同网格尺寸下模拟情况Table 2 Simulation in different grid sizes

由表2可知,当采用粗网格计算时,模拟结果存在一定误差,而采用中等及以上网格进行计算时,网格尺寸将不会对模拟得到的床层压降产生明显影响。因此,考虑计算精度和计算速度,现采用中等网格尺寸进行模拟计算,并采用有限体积法对偏微分方程进行离散,流场求解采用压力速度耦合的SIMPLE算法[18],动量、湍动能和湍动耗散率采用二阶迎风离散格式,体积分数采用Quick离散格式。

4 模拟结果及分析

4.1 模型验证

为验证模拟结果的准确性,首先对5种不同入口流速下干馏炉内总压降进行模拟,并将模拟结果和经验公式计算所得的理论值进行比对,采用由Stankiewicz[19]总结的计算固定床床层压降经验公式进行计算,式(9)～式(12)如下:

(9)

(10)

(11)

(12)

式中:umax为气体热载体流经固定床层时的最大速度；Re为基于固定床层直径和最大流速umax的Reynolds数,1≤Re≤3×105。

图2将模拟结果与经验计算结果进行对比。可以看出,随着入口流速的增加,理论计算值与模拟值均呈增大趋势。气体在床内流动时,受到固体颗粒阻力的影响,速度越大,阻力越大,因此床内压降越大。由于实验时颗粒的孔隙率是不等的,而模拟时采用各向同性情况计算,因此理论计算值偏高是合理的,且从实验的角度来看,该模拟值与理论计算值的吻合程度较好,虽存在一定误差,但总体误差在合理范围之内。

图2 模拟压降与经验压降对比Fig.2 Comparison between simulated pressure drop and empirical pressure drop

图3 对数坐标系下模拟压降与入口速度的关系Fig.3 Relationship between simulated pressure drop and inlet velocity in logarithmic coordinate system

将通过模拟得出的入口流速与压降绘制于双对数坐标系下，如图3所示，由图3可知,入口流速与压降呈直线关系。经拟合得到模拟入口流速与压降之间的关系式为

(13)

式(13)给出固定床内沿程压降与入口速度的0.783次方呈正比,这一结果与He等[20]的研究结果一致。根据以上分析可以得出:通过增添阻力源项的方法,能够对固定床内的流动阻力进行准确模拟；建立在Ergun方程基础上的多孔介质数学模型对固定床进行模拟是有效的。

4.2 压力分布

图4所示为三种结构在不同截面处的压力分布特性。图4(a)、图4(d)为布气结构优化前干馏段两截面处的压力分布,可知,在干馏段下部(Z=2 300 mm),近壁处低压区及流道中部高压区面积较大,而在干馏段上部(Z=2 800 mm),气体流经流道处加速,中心流速增加使该位置处压力减小,且气体在颗粒层中流动时受到的阻力较大,整体静压变化范围约为100 Pa。图4(b)、图4(e)和图4(c)、图4(f)分别为结构优化后干馏段两截面处的压力分布，可知,当改变布气方式后,干馏段下部低压区面积减小,在干馏段上部压力变化区域增大,但两截面处压力梯度范围降至10 Pa左右,速度均匀性得到显著提高。

图4 压力分布云图Fig.4 Cloud map of pressure distribution

图5所示为同轴撞击流布气方式下,干馏段喷嘴截面处的压力分布。由图5可知,在每个进气喷嘴处,由于气体流速的作用导致喷嘴局部的压力发生变化,干馏段两层喷嘴间压差为369 Pa,静压沿着喷嘴的中心线直至相向的两股对冲射流碰撞的共同作用面处达到最高,即在碰撞面的驻点处达到最大值。第一层喷嘴处由于受到下方气体的冲击,导致对冲的气流未能在压力最高处完全发生碰撞,而从驻点开始,静压沿着平面向两侧下降,给气体以径向加速度,这一结果与王擎[21]等的研究结果是一致的。图6所示为偏心轴撞击流布气方式下,干馏段喷嘴截面处的压力分布。如图6所示,在每个进气喷嘴处,由于气体流速的作用,在喷嘴局部地方仍然会产生压力的变化,干馏段两层喷嘴间压差为492 Pa,这一点与同轴撞击流布置下的结果是相似的。通过对比观察可知,结构优化后两种布气方式下,喷嘴附近形成的压差给予气体径向加速度,气体横向流动的加强拓宽了布气范围,促使气体混合均匀,且偏心轴撞击流方式下喷嘴截面处压力变化范围略大,喷嘴两侧气体的横向扰动相比于同轴撞击流方式得到增强,在气流撞击的交合面处,静压达到最高且具有较好的对称性。

图5 同轴撞击流干馏段喷嘴截面压力分布Fig.5 Dry distillation section nozzle section pressure distribution of the coaxial impinging flow

图6 偏心轴撞击流干馏段喷嘴截面压力分布Fig.6 Dry distillation section nozzle section pressure distribution of the eccentric shaft impinging flow

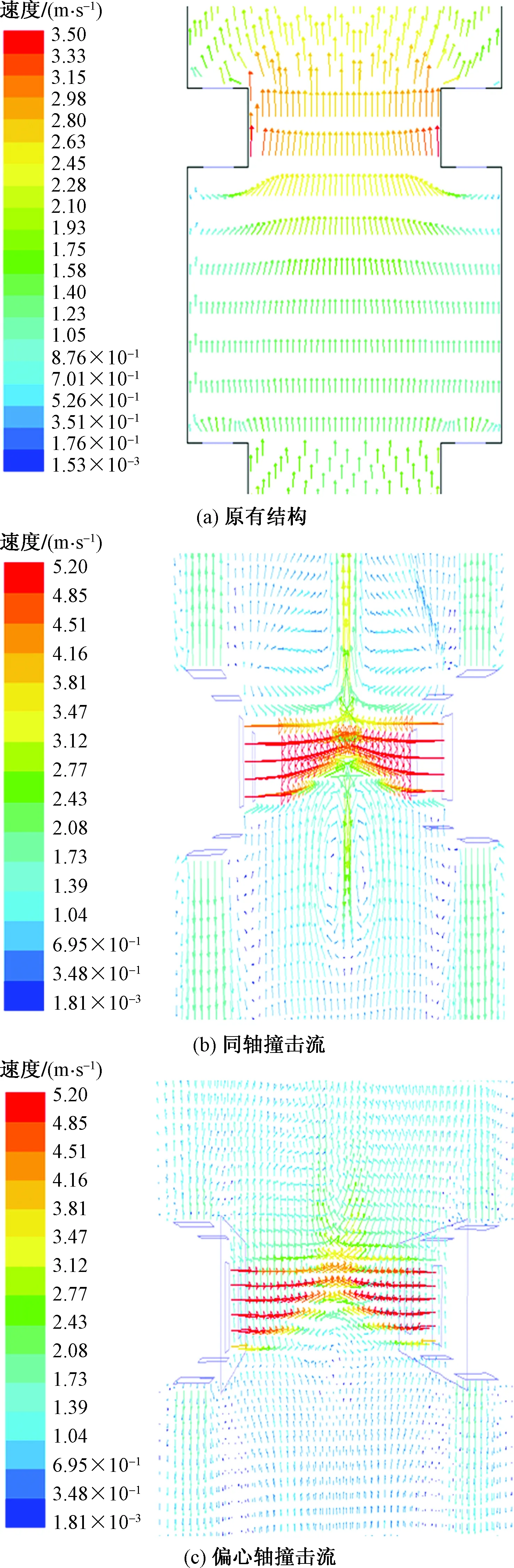
图7 轴向截面速度分布矢量图Fig.7 Axial section velocity distribution vector

4.3 速度分布

图7、图8所示分别为干馏段轴向截面及喷嘴截面处速度分布矢量图。由图7(a)可知,结构优化前,速度分布均匀性差,气体混合强度较低且横向扰动较弱,导致干馏段速度分布存在一定死区。图7(b)、图7(c)给出结构优化后干馏段轴向截面的速度分布，可知,喷嘴附近气体以较大的径向速度流向中心,在下方气流和喷嘴射流的共同作用下,中心处的轴向速度最大且从中心向壁面逐渐减小。在同轴撞击流方式下,由于撞击区域的静压高及流速差对周围气体的卷吸作用和底部大量气流的作用下,相互撞击之后轴向的速度会产生一定的变形,且撞击后速度向上下方向扩展,上一层的气流经撞击后向下的分量与下一层撞击后向上的分量形成局部漩涡。而在偏心轴撞击流方式下,由于喷嘴错位布置,气流并未产生明显的交合面,轴向扰动弱但整体速度分布均匀性较同轴撞击流得到提高,保持在1.4～1.75 m/s。

图8为两种布气方式下喷嘴截面速度分布。如图8所示,气体经喷嘴射出,相遇前各自方向没有改变,且由于每组对应的喷嘴直径和速度相等,使两股初始动量相等的射流准确地在干馏段中间相撞,产生不同程度的变形,相互作用形成了稳定、对称的涡流,使气流横向扰动增强,从而达到了强化混合的目的。从另一方面来看,涡流的形成使气流横扫大部分干馏段空间,布气范围得到拓宽,提高干馏段热载体充满度,强化干馏效果。综合压力及速度的分布,可以得出,无论采用同轴还是偏心轴撞击流布置,均能形成良好的速度场及压力场,在干馏段形成的涡流均能够使气流充分混合、气体与固体颗粒之间充分接触、干馏段速度分布均匀且无死角,从而达到强化干馏效果的目的。本文提出的布气方式,在一定程度上解决了气体热载体干馏炉因布气方式的局限性所导致的问题,这也将对今后开发大容量气体热载体干馏炉提供理论支撑。