聚合物驱油井无因次流入动态方程及其应用

王 全, 康晓东, 陈冠中, 未志杰, 刘玉洋

(海洋石油高效开发国家重点实验室, 中海油研究总院有限责任公司,北京 100028)

聚合物驱已在中国大庆、胜利、渤海等几大油田得到广泛应用,取得了明显的降水增油效果,为油田的稳产上产做出了重要贡献[1-6]。针对聚合物驱油井产能规律的研究也在持续开展,取得了丰富成果[7-8]。油井的流入动态关系(inflow performance relationship，IPR)曲线是分析油井生产状态的基础,也是确定油井合理工作制度的依据,所以流入动态曲线研究的重要性不言而喻。在聚合物驱油过程中,含有聚合物的油井产出液表现出明显的非牛顿特性,且流变参数在渗流过程中会发生变化,因此常规的油井流入动态模型不能用于分析聚驱油井的流入动态关系。针对这个问题,专家学者们持续开展研究,建立了不同的聚合物驱油井流入动态模型[9-12]。李福军等将聚合物溶液看作幂律流体,建立了聚驱油井产能预测的数学模型[13]。岳湘安等考虑了聚合物溶液的流变参数在渗流过程中的变化,分析了流变参数对流入动态的影响[14]。夏慧芬等从修正达西运动方程和拟塑性流体的运动方程出发,建立了聚驱油井的流入动态模型[15]。韩光明等[16]则进一步考虑了聚合物溶液的黏弹性及渗透率变化等因素,推导了聚驱油藏的油井产能预测模型。模型研究虽取得了较大进展,但是伴随考虑因素的增多,模型的数学形式变的愈加复杂,使得这些模型的求解普遍较为困难,不便于现场应用,流入动态分析方法的简便适用性还需进一步提高。试图以聚驱油井的理论无因次流入动态方程为指导,以油藏数值模拟技术为手段,研究不同条件下的聚驱油藏的油井流入动态状况,仿照Vogel处理溶解气驱油藏无因次流入动态方程的研究思路,对数值模拟结果进行非线性拟合,回归得到统一形式的无因次流入动态方程,提高现场应用的简便性,现场工程师能够根据方程快速方便的得到油井的流入动态关系,从而为该类油藏油井的生产动态分析和合理工作制度制定提供一定参考。

1 聚驱油井无因次流入动态方程

基于已有聚驱油井产能预测模型[13-15],考虑到聚合物溶液的黏弹性以及近井地带渗透率的下降,不考虑岩石、流体的压缩性及重力影响,将状态方程、运动方程代入连续性方程,得到流体在多孔介质中稳定渗流的基本微分方程,结合内边界定产、外边界定压的定解条件,得到流体流入动态方程为

(1)

式(1)中：Pe为泄油边界压力,Pa；Pwf为井底流压,Pa；Q为油井产量,m3/d；h为油层有效厚度,m；μ有效为流体在地层中的有效黏度,Pa·s；Re为泄油半径,m；Rw为井眼半径,m；n为流性指数；kr为流体流动时的地层渗透率,mD。

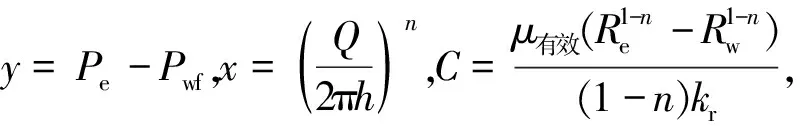
y=a(Cx)b

(2)

通过两次稳定试井资料即可求得参数a和b,流入动态方程就可表述为

(3)

Pe-Pwf=AQnb

(4)

当井底流压为0时,产量达到最大,即

(5)

式(5)中:Qmax为最大产量,m3/d。

则式(3)可无因次化表示为

(6)

式(6)即为聚驱油井的无因次流入动态方程,表明产量与流压之间存在该种形式的数学关系。无因次流入动态方程的建立为后续方程拟合工作奠定了理论形式上的基础,能够指导如何对流入动态数值模拟结果进行处理,以便发现其中存在的规律。

2 流入动态数值模拟研究

Vogel根据若干典型溶解气驱油藏油井流入动态的数值模拟结果,回归得到了适用于该类油藏油井的无因次流入动态方程,该方程可以很方便的应用于现场油井流入动态分析[17]。借鉴Vogel的研究思路,仿照其研究方法以求获得适用于聚驱油藏的无因次流入动态方程。为此,需首先针对聚驱油井的流入动态开展数值模拟研究。

2.1 基础模型的建立

首先建立聚驱数值模拟模型,基础模型采用41×41×10的网格系统,x、y方向的网格长度为6 m,z方向的网格长度为1 m。井网采用五点法布井,中间一口生产井,周围四口注水井,选择定压注入、定产量生产的生产制度。具体的油藏和流体参数如表1所示。模拟油井在不同聚驱开发阶段、不同产量条件下的井底流压变化情况,记录每个压力条件下对应的产量,即可得到不同开发阶段的流入动态曲线。

表1 油藏和流体参数Table 1 Reservoir and fluid parameters

2.2 模拟结果分析

利用建立的数值模拟模型,模拟了不同开发阶段不同产量下的压力状况,得到的聚驱油井的流入动态曲线如图1所示。结果表明,聚驱的流入动态曲线与常规水驱有明显不同的特点,众所周知,水驱流入动态曲线在直角坐标系下为一上凸的曲线,而聚驱流入动态曲线却表现为一上凹的曲线。原因在于,聚合物驱溶液在油藏中的渗流阻力更大,在相同的生产压差下,油井的产量相较于水驱就更低。随着含水率增大,流入动态曲线逐渐向外扩张,即在相同流压下,产量逐渐升高。原因在于,随着含水率增加,地层流体的黏度相对变低,流体流动性更强,相同流压下的产量就会增加。对比代表不同开发阶段的不同含水率条件下的流入动态曲线可以发现,曲线形态非常相似。结合建立的无因次流入动态方程[式(6)]的形式,以之为指导,将不同的流入动态曲线进行无因次化处理,得到的无因次曲线如图2所示,结果表明,三条无因次流入动态曲线几乎重合。通过进一步研究发现,不同油藏条件、不同流体性质、不同聚合物溶液性能条件下的无因次流入动态曲线具有相似的特征,这为采用类似Vogel的研究方法研究聚驱无因次流入动态方程提供了可能性。

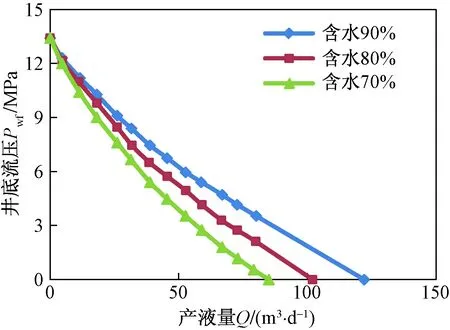
图1 基础油藏模型的IPR曲线Fig.1 The IPR curve of the basic reservoir model

图2 基础油藏模型的无因次IPR曲线Fig.2 Dimensionless IPR curve of the basic reservoir model

3 流入动态方程的拟合

实践表明,影响聚驱油藏油井流入动态的因素很多,为此分别针对不同油藏条件、不同流体性质、不同聚合物溶液性能对流入动态的影响开展研究,建立了数十个数值模拟模型,并进行了大量的数值模拟研究。通过分析不同模型油井的无因次流入动态曲线发现,曲线形状相似且彼此靠近,且与前面建立的无因次流入动态方程[式(6)]的曲线形状具有较好的一致性,故将所有模型的无因次流入动态曲线归集在一起,仿照Vogel的研究方法进行非线性拟合回归,以求得到适用于聚驱油藏的无因次流入动态方程。按照式(6)的形式,对不同模型模拟得到的1 890多个点进行拟合处理,结果如图3所示,拟合得到的无因次化流入动态方程为

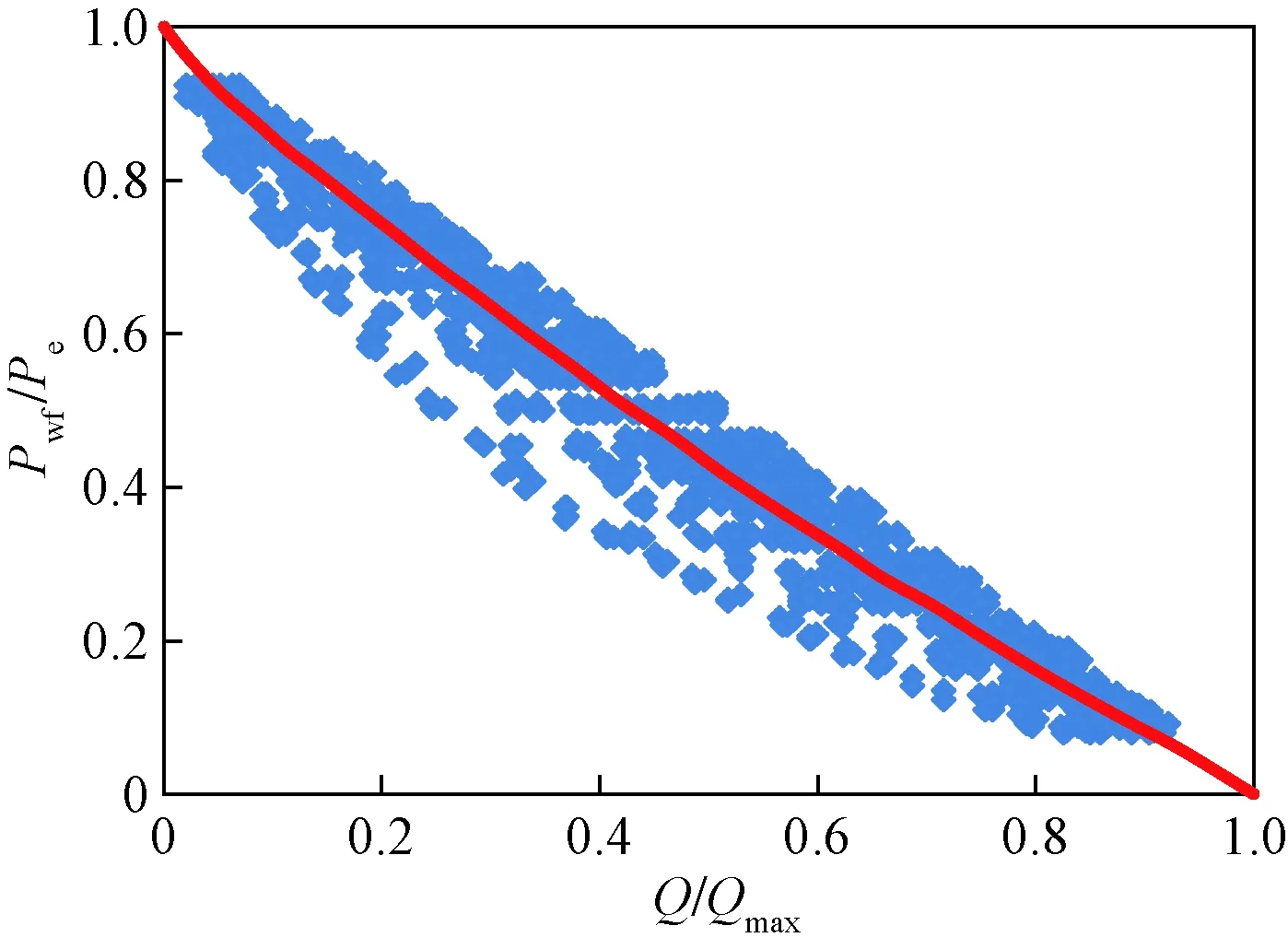
图3 无因次IPR曲线拟合结果Fig.3 The fitted curve of dimensionless IPR

(7)

拟合该方程的意义在于,可以在不涉及具体油藏参数及流体性质资料的情况下,只需要目标油井的一组流压和产量测试数据,就可以得到该井的流入动态曲线,进而预测不同井底流压条件下的油井产量,应用非常方便。通过对不同油藏条件、不同流体性质、不同聚合物溶液性能模型结果的进一步对比发现,含水率偏低、原油黏度偏高、孔隙度/渗透率偏大等几组模型的结果较为偏离拟合得到的无因次流入动态曲线,因此对于具有以上特点的油藏,聚驱无因次流入动态方程还需谨慎使用。

为了验证方程的合理性,建立一个全新的聚驱模型,开展数值模拟计算,分别绘制利用数值模拟和无因次流入动态方程得到的不同开发阶段的流入动态曲线,如图4所示。对比发现,这两种方法得到的曲线具有较好的一致性,最大误差出现在用小生产压差下的测试资料来预测最大产量,一般误差低于8%,随着开发程度的提高,误差有所增加,但仍在合理范围内。因此,利用该方程来计算聚驱油井的流入动态完全能够满足现场的工程需要。

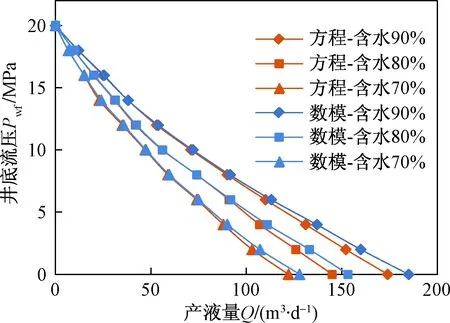
图4 不同方法计算的IPR曲线对比Fig.4 The comparison of IPR curves from different methods

4 实例计算与分析

大庆油田首开中国聚合物驱采油之先河,油藏管理模式先进,聚驱动态监测数据完备且严谨,故选取大庆油田一口聚驱油井的实际数据为例开展实例计算,以验证无因次流入动态方程的可靠性[14]。该油井油层有效厚度13.8 m,孔隙度26.7%,渗透率475 mD,油藏平均压力10.37 MPa,油井与注聚井之间的距离为212 m。测得的稳定试井资料见表2,测试时油井的工作状况正常,在录取每一个产量的同时,下入压力计测取流压,共获得了四组产量和流压数据。利用无因次流入动态方程分析该井的生产动态,采用井底流压为2.51 MPa条件下的一组产量和流压测试数据为基础,代入方程即可获得最大产量,得到该油井的流入动态曲线,进而就能够预测其他三个不同井底流压条件下的产量,产量计算结果以及计算值与实测值的对比如表2、图5所示。结果表明,流入动态曲线表现为一上凹的曲线,符合聚合物驱非牛顿流体的流动特征。三个产量计算值与实测值的最大差值为6.5 m3/d,最大相对误差为7.56%,平均误差为3.90%,计算结果与实测数据误差较小,具有较高的计算精度。从图5也可以看出,实测数据非常靠近计算得到的流入动态曲线,两者之间的吻合度较好,从而进一步验证了无因次流入动态方程的可靠性,可用来分析聚驱油井的流入动态,能够为油井合理工作制度的制定提供参考。

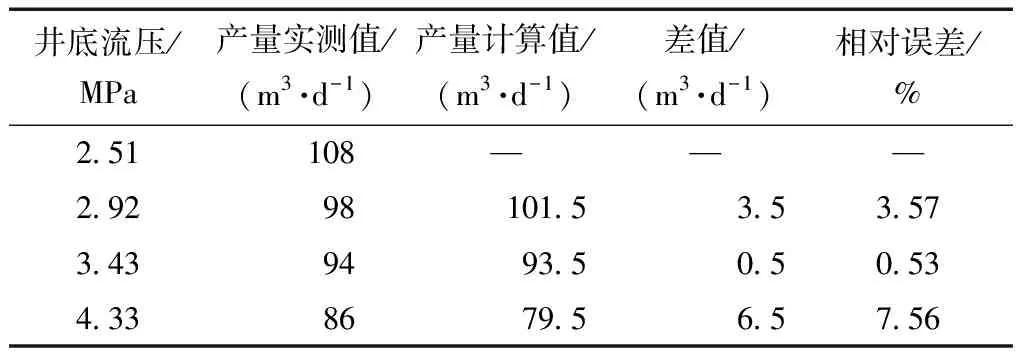
表2 油井流入动态计算值与实测值对比Table 2 Comparison of calculated oil well inflow performance values and measured value

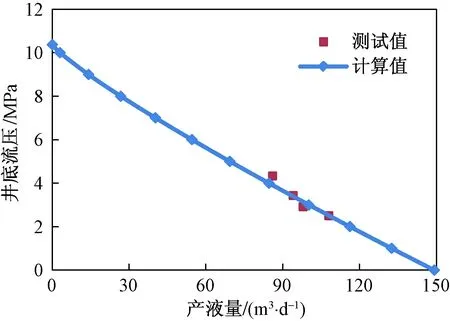
图5 油井流入动态计算值与实测值对比Fig.5 Comparison of calculated oil well inflow performance values and measured value

5 结论

(1)基于已有聚驱油井产能预测模型,考虑聚合物溶液黏弹性以及近井地带渗透率下降,结合内边界定产、外边界定压的定解条件,并经过无因次化处理得到无因次流入动态方程,该方程形式简单,便于处理。

(2)数值模拟研究表明,聚驱油井的流入动态曲线不同于常规水驱,为一上凹的曲线。不同条件下的流入动态曲线形态具有相似性,无因次化处理后各条无因次流入动态曲线几乎重合,可以借鉴Vogel的方法来研究流入动态。

(3)针对不同油藏条件、流体性质、聚合物溶液性能进行了大量的数值模拟计算,得到的无因次流入动态曲线形状相似且彼此靠近。将所有的数据点仿照Vogel的处理方法进行非线性拟合回归,得到了聚驱油井的无因次流入动态方程。

(4)实例计算结果表明,油井在不同井底流压条件下的产量计算结果与实测数据的平均误差为3.90%,具有较好的吻合度,验证了无因次流入动态方程的可靠性,可用来计算聚驱油井的流入动态,能够为油井的生产动态分析和合理工作制度制定提供参考。