基于集合经验模式分解和公共空间模式的脑电信号特征提取
2020-02-24张学军黄丽亚成谢锋
张学军, 霍 延, 黄丽亚, 成谢锋
(1.南京邮电大学电子与光学工程学院,南京 210023;2.南京邮电大学射频集成与微组装技术国家地方联合工程实验室, 南京 210023)
脑-计算机接口(brain-computer interface, BCI)与传统的神经-肌肉运动输出途径不同,它产生从大脑皮层到接收装置的信号,如轮椅、康复机器人或假肢,创建了一个新的通信通道[1]。该技术运用的方法主要是非侵入方法进而来反映出脑活动和精神状态,脑电(electroencephalography,EEG)是常见的建立BCI系统的方法。脑-计算机接口的发展解决了神经肌肉系统严重受损并与外界沟通的问题,它代替了传统的神经肌肉通道直接通过意念来与电脑程序交流并能够控制外部设备。近年来,由于神经学科、模式识别、信号处理和电子测量技术的推动,脑机接口技术引起了越来越多的关注。
BCI技术包含五个主要部分,其中,如何有效提取出脑电信号的特性并提升分类的正确率是BCI技术研究的重点。提取信号的特征最直接的方法是从频域和时域单独的研究EEG信号,常见的时域特征分析方法主要有:波形特征描述和自回归(auto-regressive,AR)模型;常见的频域特征分析有能量谱与功率谱等。近几年,公共空间模式(common spatial patterns,CSP)作为一种特征提取的方法得到了普遍的运用,公共空间模式算法成功的构造了一组用于检测事件相关去同步(event related desynchronization, ERD)/事件相关同步(event related synchronization, ERS)[2]效果的空间滤波器。Koles于1991年首次将CSP 方法来提取EEG信号中的非正常成分;文献[3]首次将CSP运用于运动想象脑电图的分类中;但是因为单独使用CSP缺乏频域信息性;杨帮华等提出了小波包分解 (wavelet packet decomposition, WPD)与CSP相结合的方法提取运动想象脑电信号特征[4]。
CSP特征提取算法的性能取决于工作频带,为了确定这样一组频带,已经提出了几种基于CSP的算法。一种方法是CSP算法在状态空间扩展:公共空间谱模式算法(common spatio-spectral pattern, CSSP)[5],采用了时间推迟算法,对每一个通道进行空间滤波与频率滤波,就分类精度而言,CSSP算法的性能优于CSP。然而,由于单次延迟的限制,CSSP方法的频率选择性很差。对CSSP做出进一步的改善,提出了公共稀疏光谱空间模式(common sparse spectral spatial pattern,CSSSP)的方法,然而,由于优化问题固有的性质,在很大程度上求解滤波器的系数依赖于初始点[6]。
上述基于CSP滤波器的方法不能找到与运动想象相关的脑活动的多个频率带,将会影响运动想象BCI系统的性能。为了解决这个问题,本文提出了集合经验模式分解(ensemble empirical mode decomposition,EEMD)结合FIR滤波器组与CSP的脑电信号特征提取的方法(ensemble empirical mode decomposition combines the finite impulse response filter and common spatial patterns,EE-FCSP),该方法在CSP的基础上结合了EEMD的频域信息,并且经过滤波器组过滤优化,用于从运动想象任务中提取特征并对其进行分类,以获得更高的准确性。
1 EE-FCSP算法
1.1 集合经验模式分解
EMD方法可以较好地处理非线性非稳定的信号,在信号处理中被广泛使用,但其得到的IMFs之间易产生模态混叠。EEMD通过向原始信号增加白噪声的方法解决了这一问题[7]。EEMD的具体步骤如下。
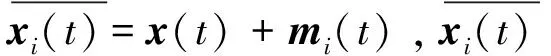
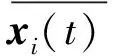
步骤3将得到的IMFs组成矩阵:
步骤4重复步骤1~3共M次。M由式(1)确定:

(1)
式(1)中:d为mi(t)的幅值系数;g为原始信号与分解得到的所有IMFs求和后计算的标准差;g越小,EEMD得到的分解结果越好。
步骤5计算所有IMFs的集合平均,即:
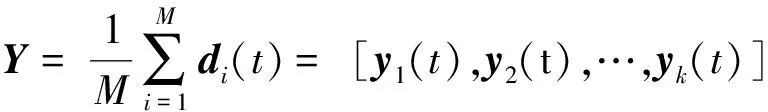
(2)
式(2)中:yi(t)是EEMD分解的第i阶IMF。
1.2 公共空间模式(CSP)
公共空间模式算法是基于对两个类别的协方差矩阵联合对角化的一种算法[8,9],算法步骤如下[10]:
步骤1两种不同类型的实验预处理后的EEG信号分别记为XH以及XF,其标准化空间协方差矩阵:

(3)
式(3)中:XH和XF为N×M的矩阵,N为导联数,M为采样点数。
步骤2求两类平均的协方差矩阵:

(4)
式(4)中:TH、TF分别为两类实验的个数;Yk={H,F}为第k次试验的类标签。
步骤3对角化复合协方差矩阵:
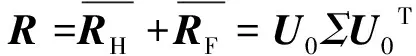
(5)
式(5)中:U0由R的特征向量组成;Σ为对应于特征向量的特征值形成的对角化矩阵。
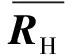

(6)
式(6)中:白化矩阵P为

(7)
步骤五对角化SH与SF:
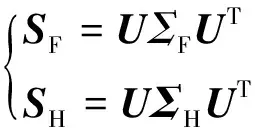
(8)
ΣH+ΣF=I
(9)
式中:I为单位向量。
步骤六得到投影矩阵W:
W=UTP
(10)
利用投影矩阵W将原始EEG信号进行转化:
Z0=WX
(11)

f=[f1,f2,…,f2m]T∈R2m×1
(12)
其中:
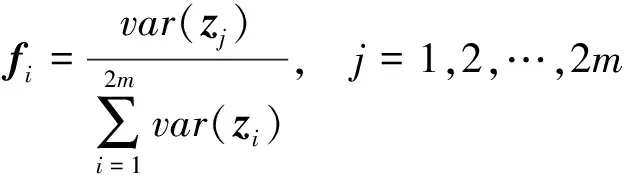
(13)
1.3 EE-FCSP算法思路
在做不同类的运动想象的任务时,与运动有关的大脑皮质部分能够产生包含μ节律(8~13 Hz)和β节律(13~30 Hz)的EEG信号,因此,研究8~32 Hz的信号可以提取与两种类型的运动想象任务相关的EEG特征。
所提算法的流程分为下述几个阶段,如图1所示。第一阶段,通过实验获得的EEG信号由8~32 Hz带通滤波器滤波;第二阶段,预处理后的结果经过EEMD得到多个模函数(intrinsic mode functions,IMFs),根据IMFs的频谱图可以看出IMFs的前三阶包含μ节律范围和β节律范围,且在5~30 Hz内,前三阶的能量也比较集中,IMF4~IMF8包含更多的低频信号,存在更多的伪迹以及噪声信号,所以选择前三阶的IMFs进行信号的重构;第三阶段,重构后得到的信号作为FIR滤波器组的输入。频率段分别为6 Hz的四个不同的带通滤波器s组成了FIR,每一个IMF经过一个滤波器组得到多个与运动想象相关的脑活动的子带信号,前三阶IMFs相同频段的信号组合成一个信号集,故重构后的信号被分解为四个子带信号集,因此获得的一组左右手的运动想象任务的原信号最终被分解为对应的四组频段信号;第四阶段, 提取每一组子带信号集的CSP特征,并将四组子带信号集的四个CSP特征进行组合形成新的特征矩阵;最后,将新特征矩阵输入到支持向量机(support vector machine,SVM)中来进行两种类型运动想象任务的分类。
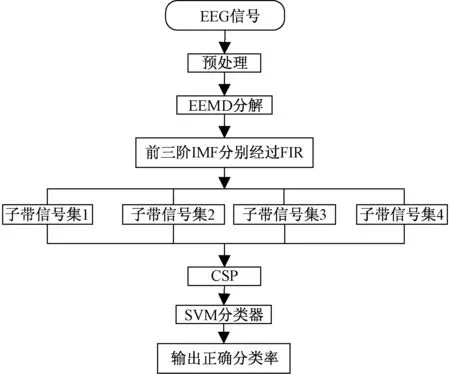
图1 EE-FCSP方法流程Fig.1 Flow chart of the EE-FCSP method
2 数据集描述
选择BCI Competition 2008 data sets 2b的数据集作为实验数据[11],9个受试者进行试验,每一个受试者的训练集由受试者执行运动想象单次试验时得到的三个电极的EEG信号组成。选择大脑皮层的C3、C2和C4的这三个电极记录产生的EEG信号,并设置采样的频率为250 Hz。脑电极分布如图2所示。

图2 脑电极分布Fig.2 The distribution of brain electrodes
9个受试者都是右利手,视力正常,受试者全身放松地坐在舒适的扶手椅上,注视着屏幕,屏幕距离眼部的距离为1 m[12]。收集到的EEG由0.5~100 Hz的带通与50 Hz的陷波滤波器处理来去除一些噪声。
实验分为两周内不同的两天进行,每一个受试者参加两个session的屏幕显示的测试,每一个session包含6组,其中一组分别包含10个左手、右手两类运动想象。因此,一组包含20次实验,一个session包含120次实验,总计可获得9个人分别对每一类运动想象的120次数据。
单次实验的过程如图3所示,屏幕显示的实验过程包括左右手两类运动想象,由图3可知,实验总共持续8~9 s的时间,在前两秒受试者处在放松的状况;第2 s时蜂鸣器响起,并且在屏幕上出现“+”标志,持续1 s的时间来提示受试者实验即将开始;在第3 s时,屏幕上的标志发生变化,出现了视觉提示箭头,该箭头随机产生,箭头指向左侧,表示被测试者需要执行左手动作想象,箭头指向右侧,表示被测试者需要执行右手动作想象,持续1.25 s的时间;在第4 s,根据屏幕所显示的标志,受试者开始进行相对应的运动想象的任务,持续3 s;在第7 s,运动想象任务停止,被试者开始休息。
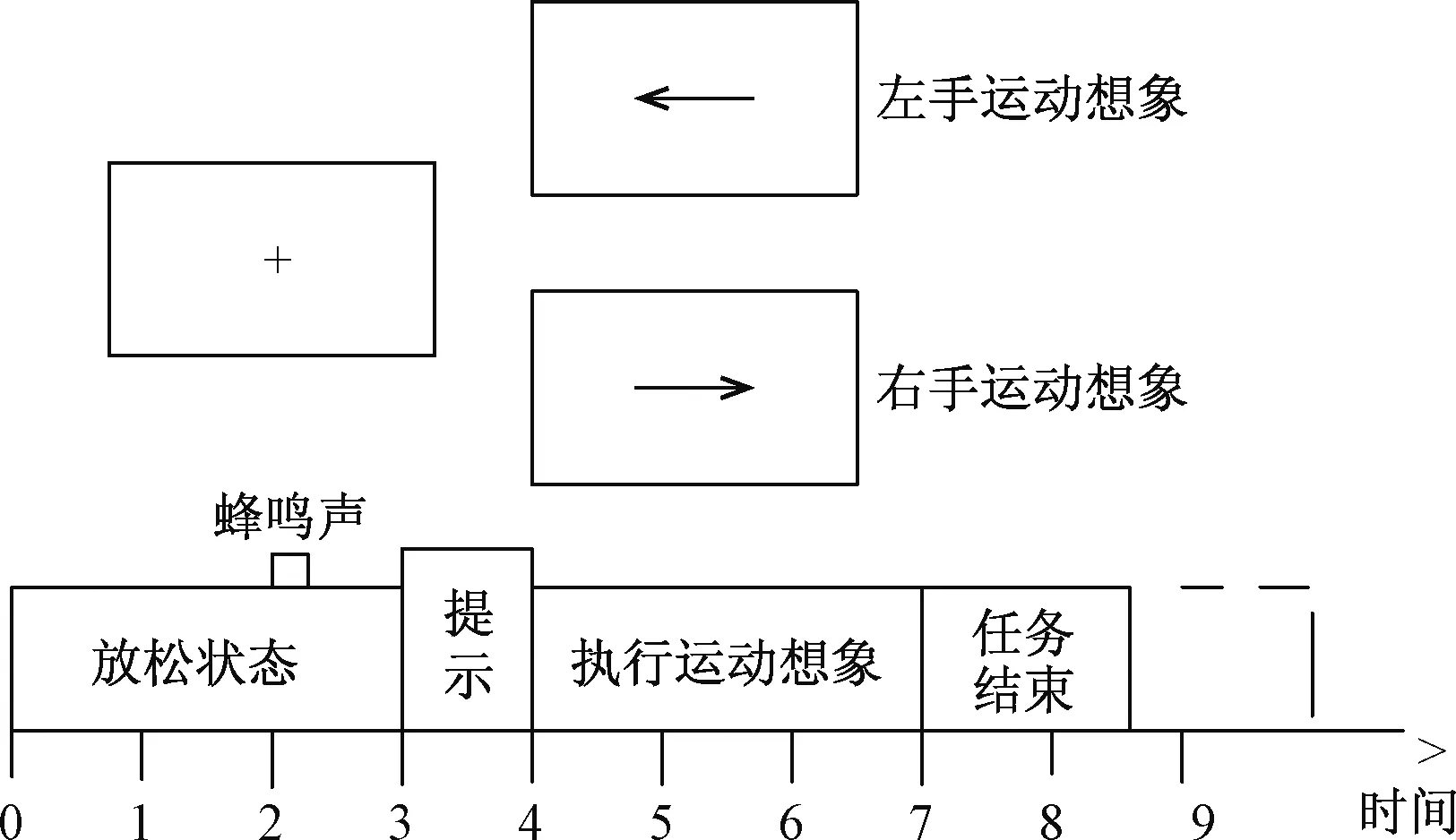
图3 运动想象时序图Fig.3 The diagram of motion imagination
3 特征提取
3.1 预处理
当受试者进行肢体运动想象的试验时,与大脑另一侧的运动感觉区域相关的μ节律与β节律伴随着能量的减少,称之为事件相关去同步(ERD);相对于同侧运动感觉区域的μ和β频率段随着能量的增多,称之为事件相关同步(ERS)[13-14]。
由上述现象可知,与不同的运动想象任务相关度最大的信号在8~32 Hz的频率段,其中5 Hz以下又多为伪迹,因此首先利用8~32 Hz的带通滤波器进行滤波预处理以便更好地去除信号中存在的伪迹。
选取被试者B01的一个trial两种类型的运动想象分别得到的C3与C4导联原始脑电波的信号,对其经过预处理后并获得预处理后的结果以及经过傅里叶变换后的频谱,如图4、图5所示,可看出滤波后的信号主要包含μ节律和β节律范围。
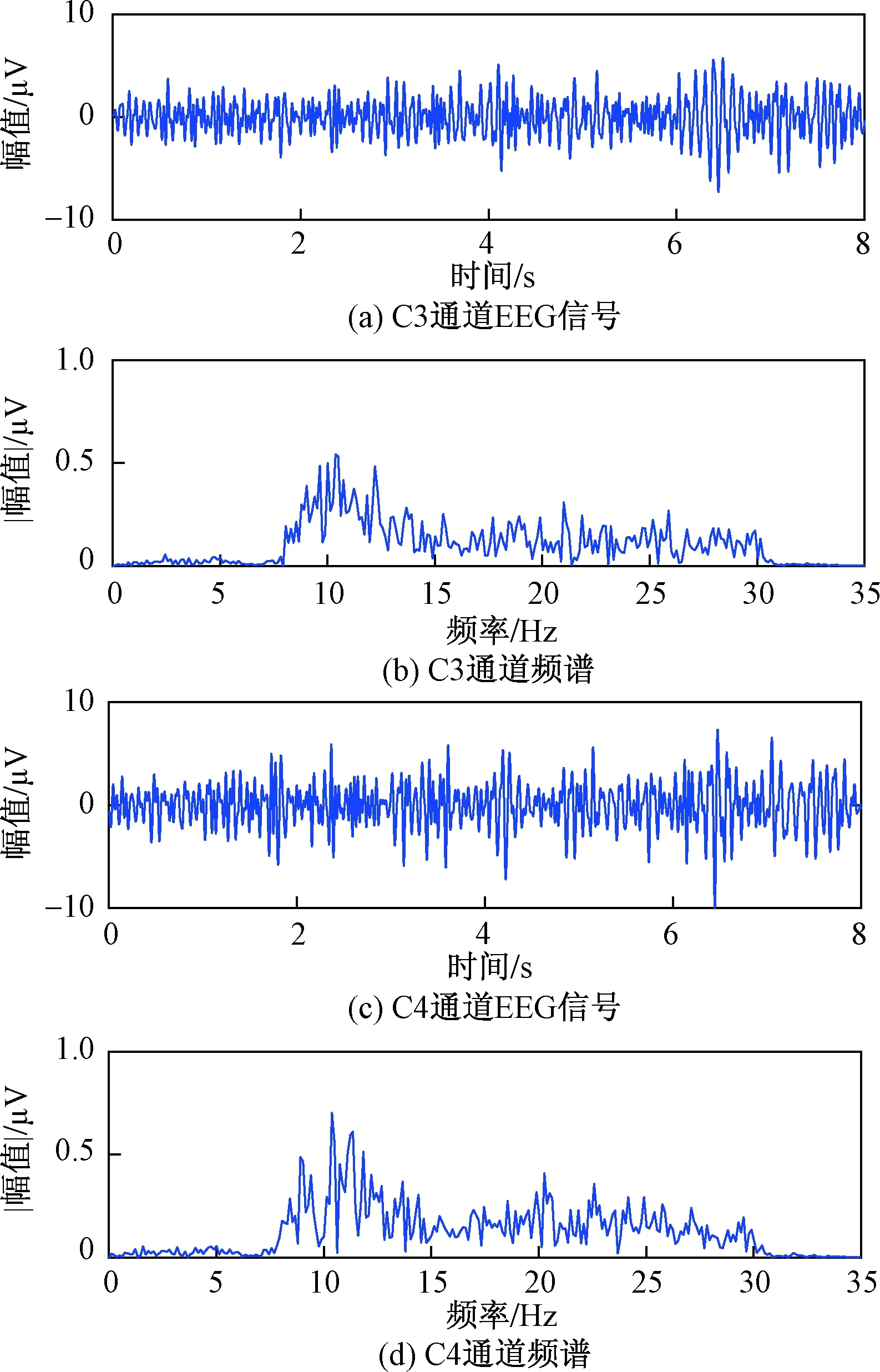
图4 左手想象运动预处理EEG信号和频谱Fig.4 EEG signal and spectrum of left-hand motor imagination

图5 右手想象运动预处理EEG信号和频谱Fig.5 EEG signal and spectrum of right-hand motor imagination
3.2 EEMD分解
上述预处理后得到的结果分别经过EEMD处理,选取C3通道对应的两类不同实验前8阶的IMFs分量并得到频谱,如图6、图7所示。

图6 左手想象运动C3通道IMFs波形和频谱Fig.6 IMFs and spectrum of C3 channel of left-hand motor imagination
3.3 IMF重构
根据EEMD处理后的频谱图可以得出,前三阶的IMF包含μ节律和β节律范围,剩余的IMF处于低频段,主要为噪声或伪迹信号,故选择前三阶的IMFs实现信号的重构,重构后的波形和频谱,如图8、图9所示。
3.4 FIR滤波器
FIR滤波器由频率段分别为6 Hz的四个带通滤波器构成,重构后的信号被分解为四个子带信号,因此一组左右手运动想象任务的原信号最终被分解为对应的四组频段信号。每一组作为CSP的输入进行特征提取。
在一组不同的运动想象任务实验中,重构后的左手运动想象C3与C4通道的信号分别为3×2 000的矩阵,组合为6×2 000的矩阵,其中6为IMF的个数,可以看作通道数,2 000为采样点数。经过FIR滤波器后得到四个6×2 000的矩阵,右手运动想象数据处理过程相同。一次左右手运动想象经过上述处理后的信号相同频段对应的矩阵作为CSP的输入进行特征提取得到一个特征向量,因此,一次实验可以获得四个特征向量构成的特征矩阵。一个session包括了120次试验,运动想象后得到60组向量,分为20组测试向量矩阵和40组训练向量矩阵,分别作为SVM分类器的输入得到分类的结果。

图7 右手想象运动C3通道IMFs波形和频谱Fig.7 IMFs and spectrum of C3 channel of right-hand motor imagination
图8 左手想象运动重构后的EEG波形及频谱Fig.8 EEG signal and spectrum of left-hand motor imagination after the reconstruction

图9 右手想象运动重构后的EEG波形及频谱Fig.9 EEG signal and spectrum of right-hand motor imagination after the reconstruction
4 实验结果与分析
4.1 实验结果
选择每一次实验的EEMD分解后的C3、C4信道的前三阶IMF重建以形成观测矢量,并且在FIR滤波器后通过CSP获得特征向量矩阵。 图10为当受试者B01执行两种类型想象运动任务时,单次试验的脑电图信号经过EEMD分解后的前三阶分量的脑地形图,从图形中可以看出,进行两种不同类型的想象运动时,C3与C4之间的能量差异相对较大;在左手想象运动实验中,C4电极比C3电极更活跃,并且C3电极在右手想象运动实验中比C4电极更活跃,该特性有效地表现出了“源”的位置,因此可以作为分类器输入的特征。

图10 想象运动前三阶IMFs特征能量脑地形 Fig.10 Brain maps of characteristic energy of motro magination of the first three order IMFs
将实验的原始信号进行EEMD 分解之后,选择出合适的IMFs进行重构,重构后的信号再经过FIR滤波器组进行滤波,每一个IMF被分成若干子带,子带信号经过CSP算法得到与EEG信号有关的特征矩阵,运用SVM对获得的特征矩阵实现两种类型想象运动的分类。图11(a)是B01~B04被试单次试验的分类精确度;图11(b)是B05~B09被试单次试验的分类精确度;由图11可见,除了个别的正确率比较低以外,分类正确率大体上是在88%~98%之间,并且92%~98%之间的比较多。可见该方法的分类性能较好并且有着较高的鲁棒性。

图11 9名被试的单次试验分类精确度Fig.11 The classification accuracy of 9 subjects in one trial
4.2 不同实验比较
下面运用相同的数据集,对不同的方法进行实验,并将每一种方法得到的特征向量作为SVM的输入进行分类。
(1)E-CSP: EMD与CSP结合,原脑电信号经过EMD得到一系列的IMFs,选择包含μ节律和β节律的IMFs重构,重构后的信号作为CSP的输入得到特征向量。
(2)E-FCSP1: EMD融合FIR滤波器结合CSP的特提取方法。滤波器组覆盖8~32 Hz的频率带,由三个频段为8 Hz的带通滤波器组成。
(3)E-FCSP2: EMD融合FIR滤波器结合CSP的特提取方法。滤波器组覆盖8~32 Hz的频率带,由四个频段为6 Hz的带通滤波器组成。
(4)EE-CSP:EEMD结合CSP提取脑电信号的特征。
(5)EE-FCSP1: EEMD融合FIR滤波器结合CSP的特提取方法。滤波器组覆盖8~32 Hz的频率带,由三个频段为8 Hz的带通滤波器组成。
(6)EE-FCSP2: EEMD融合FIR滤波器结合CSP的特提取方法。滤波器组覆盖8~32 Hz的频率带,由四个频段为6 Hz的带通滤波器组成。
利用以上方法对9个受试者分别进行实验,每个受试者得到一个session的平均分类精度及其与EE-CSP2的增量,如表1所示。
从表1中可以看出九位被试六种方案下的正确率数值以及EE-CSP2分别与E-CSP、E-CSP1、E-CSP2、EE-CSP、EE-CSP1的增量值,可以看出EE-CSP2相比其他五个方案正确率增量较为明显;除B08以外的所有受试者EE-CSP2得到了最高的分类精度;受试者B09采用E-FCSP2得到的分类精度高于EE-FCSP2,可能原因如下:一是因为EE-CSP2实验时所选取的SVM的最优参数并不是最优;二是因为采集数据不够准确。总之,从表1中可以看出,采用EEMD组合的方法得到的分类精度比对应的采用EMD组合的方法得到的分类精度有着明显的提高,尤其是EE-CSP2方法有更明显的优越性与鲁棒性。由图12可见,采用EE-FCSP2方法进行特征提取,9位受试者的所有试验的平均分类正确率在95%以上,被试者B04平均分类准确率可达到97.31%,被试B09的平均的分类准确率最低为95.55%。因此所提出的方法在特征提取上具有较好的性能。
另外,在EEMD结合CSP的基础上研究了不同FIR滤波器数对平均响应时间以及平均分类准确率的影响。通过增加滤波器的个数来处理数据,如表2所示。可以看出,随着滤波器个数的增加分类准确率增加,但同时响应时间随之增加。与较多滤波器个数相比,利用四个滤波器处理数据虽然平均分类准确率有小幅降低,但响应时间却缩短很多。EE-FCSP2以少量分类正确率为代价降低了复杂性,具有一定的实用价值。
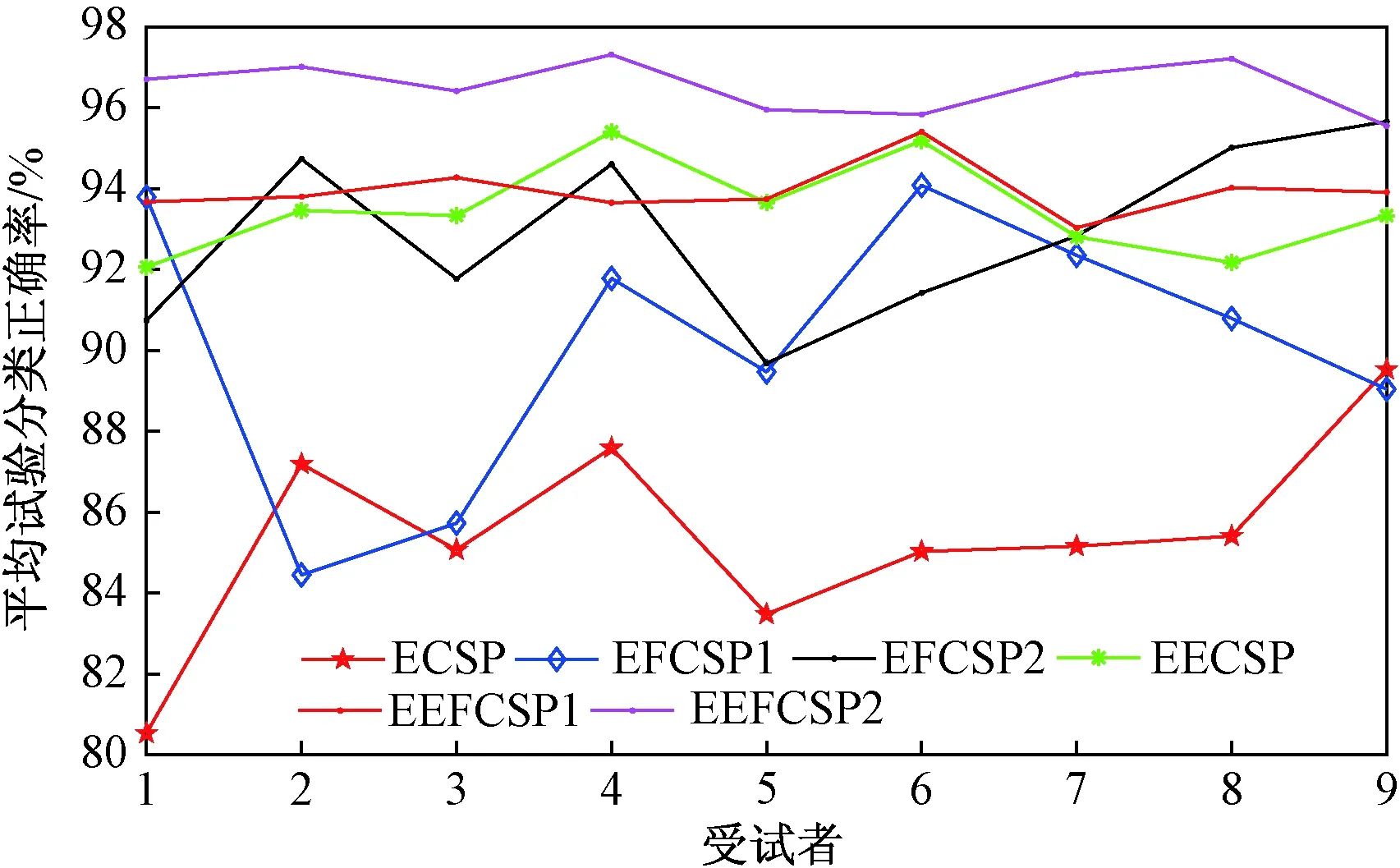
图12 六种特征提取方案中九名被试的平均分类准确度Fig.12 Average classification accuracy of 9 subjects with 6 different methods

表1 九个受试者的六种特征提取方案的分类准确率和增量对比Table 1 Average classification accuracy and increment of 9 subjects in all trials with 6 different methods

表2 不同滤波器数分类准确率比较Table 2 Comparison of the number of different filters

表3 与第三届BCI竞赛结果比较Table 3 Comparison of the results with the third BCI competition
4.3 与BCI竞赛成绩比较
将得到的结果与第三届BCI竞赛中的三组相比较,结果如表3所示。可以得出,本文方法得到分类的精度比其他三组的分类精度较高;仅选用了C3、C4两个通道进行试验,与其他试验相比,大大减少了通道数,同时也保证了分类精度。
5 结论
(1)针对CSP算法缺乏频域信息且需要较多的大量通道的信号,提出了一种EEMD融合FIR与CSP结合的算法,该方法减少了通道数目且产生了一组与运动想象有关的子带信号。
(2)利用竞赛的脑电数据集,对脑电信号进行预处理,然后采用本文方法进行处理,证明了该方法的有效性。
(3)EEMD处理或者EMD处理后,重构后的信号经过不同的FIR滤波器组取得的分类结果是不同的,当滤波器的数量增多时,分类精确度也提高;但同时复杂性随之提高。相同的FIR滤波器组的情况下,EEMD分类的精确度高于EMD的分类精确度。
(4)实验表明EE-CSP2算法有着较好的性能,其平均分类精度达到了96.53%,为基于EEG的BCI系统提供了可行的方法。然而在未来的工作中需要对该方法的复杂性以及自适应性做进一步的改善。
