输水隧洞建造过程中泵送混凝土管道的冲蚀机理

梁 爽, 南 轩, 陆金才, 丁红春, 黄剑峰*

(1.云南农业大学水利学院,昆明 650201； 2.云南农业大学建筑工程学院,昆明 650201,3.中国水利水电第十四工程局有限公司勘察设计研究院， 昆明 650051)

水利建设工程中冲蚀磨损问题是含两相流泵送混凝土工程中常遇到的大难题之一。在研究混凝土流动性方面,肖煜等[1]研究发现,由于水泥水化作用会产生大量的Ca(OH)2和 C—S—H等水化产物,会增加流动浆体体系黏度,从而使混凝土的坍落度经时损失增大,因此研究混凝土坍损的实质在于研究混凝土的流变性特征。田正宏等[2]在研究混凝土流变性过程中得出粉煤灰的掺入量对非连续级配混凝土影响较大。通过大量泵送混凝土实际工程,发现混凝土在管道内流动属于两相流,对管道的拐弯处有着严重的冲蚀破坏。在类似管道冲蚀数值模拟研究中,许留云等[3]指出工程上的冲蚀磨损是指材料表面受到粒子的反复冲击,实质上是材料在冲击过程中的动态损伤和破坏过程。目前中外的主要研究大多集中在油、气管道内多相流中的粒子对弯管处冲击导致磨损而发生破坏[4-5],主要的原因是材料颗粒在有压泵送过程中对弯管处的钢管冲蚀。白莉等[6]研究发现不同含砂量与砂子的种类对弯管冲蚀磨损情况各不同。曹辉祥等[7]发现气体与固体两相流管道处弯管是冲蚀破坏最严重的部位,且不与工况环境有关。金浩哲等[8]利用相似理论模拟出弯管冲蚀瞬态特性,也将剪应力作为表征冲蚀的重要指标。在两相流对管道冲蚀研究中,大多是气液、固液、气固等输油、气试验[9-10],鲜见有对泵送混凝土在管道内流动产生的冲蚀破坏进行数值模拟研究。通过龙开口水电站1号输水隧洞泵送混凝土过程中弯管处发生的磨损情况,用数值模拟方法研究管道的冲蚀磨损机理,发现混凝土泵送过程中粗骨料对管道的磨损是导致泵送混凝土摩擦阻力增加的原因,进而产生泵送速度、管内压强等方面的变化,因此分析其冲蚀机理找到管道磨损原因对工程施工的顺利完成是极为重要的。

1 数值模拟方法

1.1 流动控制方程

泵送混凝土的过程中水泥、减水剂、砂石等组成了多相流体,由于砂石颗粒的存在需要基于颗粒流动力学了解其在泵送过程中各相组分之间的相互作用的力学特性[11]。混凝土可以看作是一个粗骨料和水泥浆组成的固液两相流系统,满足流体连续性方程

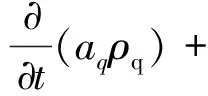
(1)

式(1)中:aq为q相的体积分数；ρq为q相的密度；vq为q相的速度；mpq是相p到相q的传质,mqp是相q到相p的传质；Sq为源项，常为常数，缺省值为0。

将多相流理论中体积分数引进到系统质量、动量守恒方程中,形成分析泵送混凝土的控制方程如式(2)～式(6)。

体积分数：

ρ=∑αqρq

(2)

ρ=α2ρ2+(1-α2)ρ1

(3)

第q相的有效密度为

(4)

第q相的动量方程为

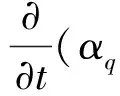
(Fq+Flift,q+Fvm,q)

(5)

式(5)中：g为重力加速度；Fq为外部体积力；Flift,q为升力；Fvm,q为虚质量力；Rpq为相间相互作用力；p为各相共享的相同压力；τq为第q相的应力-应变张量:

(6)

式(6)中：μq和λq分别为第q相的剪切黏性系数和体积黏性系数；vq为q相的速度。

1.2 湍流模型

采用标准k-ε方程模型,其湍流动能k和耗散率ε的方程如式(7)、式(8):

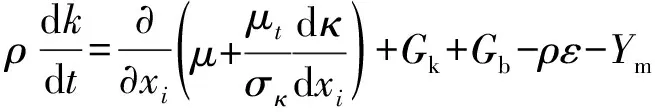
(7)

(8)

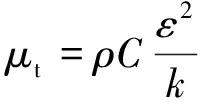
1.3 冲蚀模型

基于DPM离散相模型中的颗粒运动方程对时间的积分可以得到颗粒运动轨迹。根据不同速度、不同经验等各个因素的综合影响得出以下冲蚀模型：

(9)

式(9)中:f(θ)为冲击角度函数；v为颗粒冲击速率,m.s-1；Aface为粒子冲击壁面的单元表面积,m2；b(v)为速率指数函数常数,b(v)=2.6；C(dp)为颗粒直径函数,C(dp)=1.8×10-9;Rerosion为冲蚀磨损率,kg/m-2;mp为颗粒质量流率,kg/s。

2 计算模型

几何模型如图1所示,管道的直径d=150 mm, 壁厚h=8 mm,弯曲段半径R=1 000 mm,几何尺寸L1=395 000 mm,L2=2 960 mm。管道材料为碳钢,其弹性模量为 200 GPa,泊松比为 0.31,密度为7 850 kg/m3。弯管内部的流动介质为C25混凝土,其密度由组成各相确定,动力黏度由流动黏度和材料参数确定。

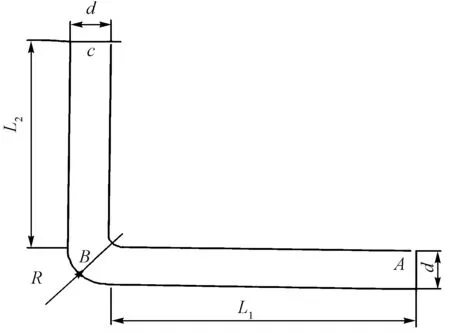
图1 泵送混凝土管道几何模型Fig.1 Model of concrete pumping pipe

施工时混凝土温度设置20 ℃,动力黏度为21 pa·s[12-13],流体设置按照龙开口输水隧洞泵送混凝土的配合比要求:水灰比0.493,砂率45%,粗骨料最大粒径为31.5 mm,密度为2 454 kg·m-3。此时每立方混凝土不添加外加剂。各相体积分数按照每立方米各材料所用质量除以密度,具体的颗粒体积分数如表1所示。

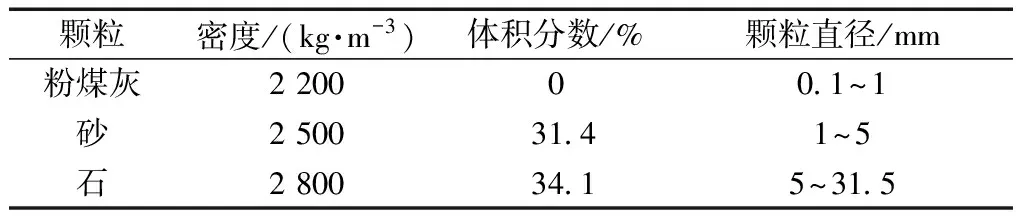
表1 泵送混凝土每立方骨料组成Table 1 Per cubic aggregate composition of pump concrete

用四面体单元划分几何模型网格。如图2所示,经网格无关性验证最终确定网格数量为156 321,在弯管处设置网格加密,将入口(A 端) 设置为速度入口,速度为10 m·s-1; 将出口(C 端) 设置为压力出口,压力为15 MPa; 对整个管道施加9.81 m·s-2重力加速度,在弯管A、C两端环形面上施加固定约束[14]。

图2 泵送管道的网格划分模型Fig.2 Grid partition model of pumping pipeline

3 结果分析

在模拟实际工况下泵送过程达到稳定时的质量流量为24.098 kg/s,与龙开口的实际的泵送量85 m3/h基本吻合,说明数值模拟方法基本正确。管道水泥、细砂、石子体积分数分布分别如图3所示。由图3可知， 颗粒直径在0～10 mm的砂子能快速通过弯管处不会沉积,10～31 mm的石子大量沉积在弯管处,造成弯管堵塞。由于固体颗粒在弯管处的冲击和碰撞导致其速度与压力位移增大,故模拟显示出混凝土各相体积分数在弯管处有所堆积。

图3 水泥、细砂、石子体积分数分布Fig.3 Distribution of the volume fraction of ement, fine sand and pebble

图4 出口处冲蚀磨损率分布Fig.4 Distribution of the erosion rate at outlet

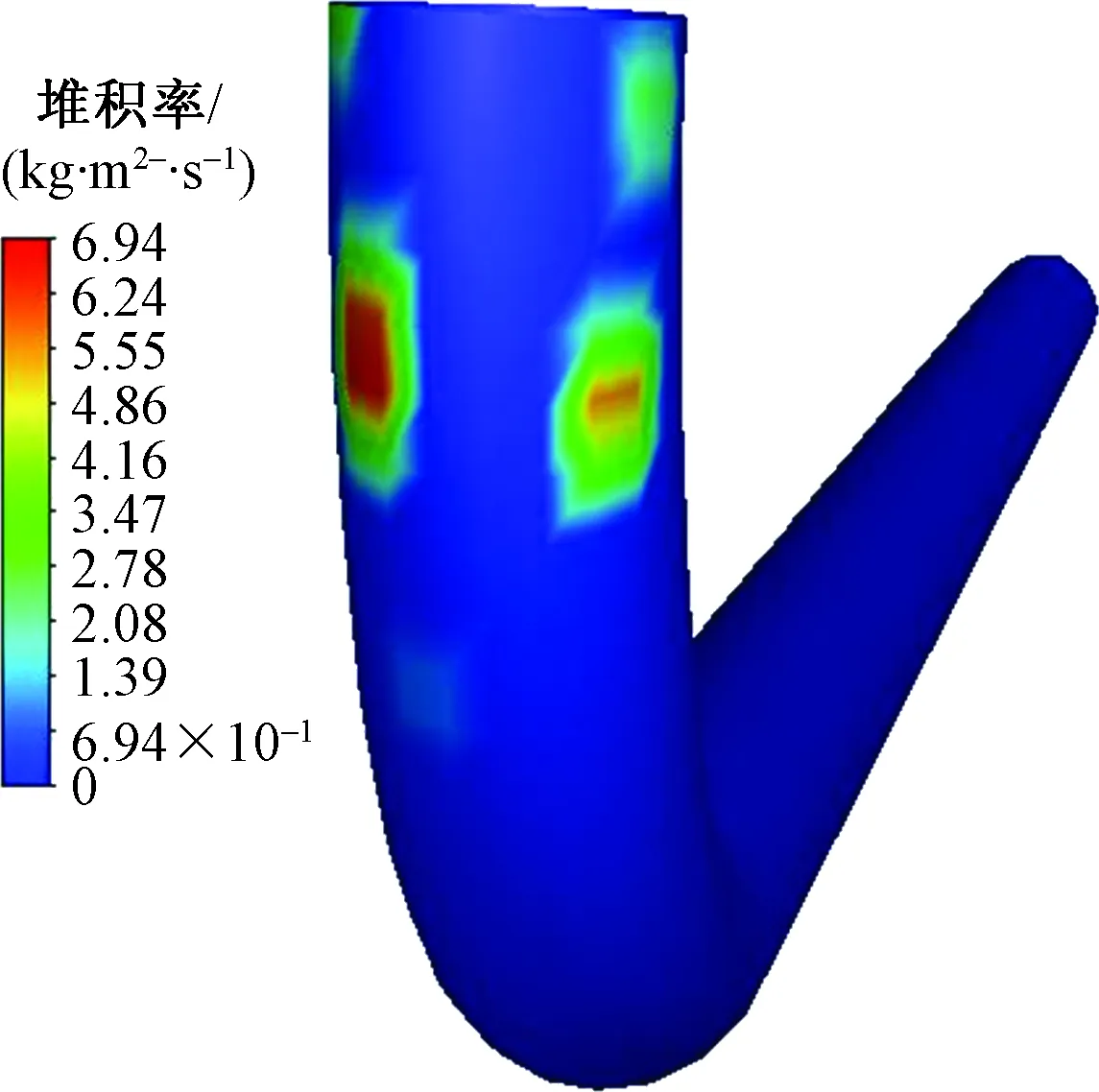
图5 出口处颗粒堆积率分布Fig.5 Distribution of accumulation rate at outlet

管道出口处冲蚀磨损率分布如图4所示,管道出口处颗粒堆积率分布如图5所示。磨损速率在弯管出口因颗粒堆积而变大,颗粒对管道产生作用力增大导致其磨损的可能性增大，且弯管内冲蚀磨损最严重的部位位于弯头外侧80°～90°之间。

管道内颗粒流速随时间变化曲线如图6所示,管壁压强随颗粒堆积位移曲线如图7所示。由图6可知，随着时间变化管道中混凝土输送速率变小,表明可能发生冲蚀磨损或堵管情况。由图7可知，从堵管颗粒堆积处0 m计算,此时弯管处压强最大,随着颗粒堆积位移增大压强变小,充分说明在弯管处冲蚀磨损最大。实际泵送混凝土输送管冲蚀磨损位置如图8所示,与模拟结果基本接近。

图6 管道内颗粒流速随时间变化曲线Fig.6 Temporal variation in granular flow rate inside the pipe

图7 管壁压强颗粒堆积随位移变化曲线Fig.7 Wall pressure versus displacement change

图8 实际弯管处冲蚀磨损位置Fig.8 Position of the actual erosion at the bend

4 结论

基于DPM离散相模型对混凝土泵送过程中的混合多相流问题进行研究,计算结果表明，在管道出口处颗粒对管壁冲蚀磨损最严重,且发生部位在弯头外侧80°～90°,与实际工程磨损情况较为吻合。说明该模型能较好地捕捉泵送混凝土中的颗粒流动的物理力学特征,能准确预测管道最大冲蚀磨损位置。可为类似的泵送混凝土施工中管道设计或混凝土配合设计预防冲蚀磨损提供一定的参考经验。