盾构始发端垂直冻结温度场数值分析与现场实测

李晓娜, 杨双锁, 鲍飞翔, 赵智辉

(太原理工大学矿业工程学院,太原 030024)

随着近年来中国国民经济的发展以及城市人口的日益增多,城市地下空间建设逐渐变成与人类生活息息相关的项目。盾构隧道端头土体自立性较差,如果加固不当,极易造成涌水涌沙等不良现象,影响盾构机的始发与接收,并且危及周围的建筑物。人工冻结技术是对软土地层进行临时加固的一种工程常用方法,该技术除可以有效地对软弱土体进行加固外还能达到降低土体中水渗流的效果,是一种不污染环境的“绿色”施工方法。掌握冻结温度场的分布规律对于准确判断冻结效果以及控制施工有着极其重要的现实意义,也是人工冻结法的一项最基本的理论研究。针对冻结温度场的发展状况以及规律研究,中外学者通过模型试验、数值模拟、现场实测等手段已经得出了许多重要的成果。胡向东等[1]回顾总结了冻结加固法中垂直、水平冻结温度场理论与设计计算方法,并且分析了目前研究存在的问题,指明了今后的主要研究方向。吉植强等[2]通过相似模拟试验研究了当渗流速度不同和冻结管间距不同时,冻结过程中的温度场分布特征以及冻结壁的厚度变化情况。周晓敏等[3]运用人工地层冻结模型研究了水平地层冻结温度场、位移场以及地层应力,发现其规律与工程实测一致。胡俊等[4]等建立了直管冻结和半圆环形冻结两种数值模型,研究了琼州海峡隧道盾构对接工程的冻土帷幕厚度与时间之间的关系。林斌等[5]在研究矿井多圈管冻结壁温度场时运用了数值模拟与现场实测对比的方法发现:交圈顺序依次为中圈孔、外圈孔、内圈孔。吴雨薇等[6]通过数值分析,采用单因素分析法得出:降低盐水温度会扩大冻结的范围,但是-1 ℃和-10 ℃等温线构成的范围不会增大。胡俊[7]通过数值模拟得出:冻结管直径与冻结壁交圈时间存在线性关系,直径每增加1 cm,交圈时间减少大约12 h。汪仁和等[8]利用ANSYS有限元软件对单、双排管冻结壁形成进行研究探讨了双排管冻结下冻结壁平均温度的简化计算方法。杨平等[9-11]运用数字测温系统监测了南京地铁集庆门站冻结加固地层温度发现:相对含水率而言,土质对于冻结温度有着更大的影响；冻结壁形成过程中土体中的空气和地下水流动会减缓甚至阻碍其形成。

目前，冻结法相关研究中,理论较为成熟的是传统煤矿立井冻结,在地铁施工项目中,城市小断面隧道水平冻结应用较为广泛,对垂直冻结施工进行数值模拟并且与实测数据结合方向的研究相对较少。冻结帷幕温度场的形成非常复杂,而冻结帷幕的平均温度、有效厚度是人工冻结技术成功的重要指标[12]。因此,研究其温度场的发展规律和特征具有重要现实意义。针对太原地区的特殊施工环境与土质,运用有限元软件模拟冻结帷幕在不同时间的温度发展情况,并实时监测冻结帷幕温度场和盐水温度变化,通过对比分析论证模拟的可行性,以此为依据可以更加准确地预测冻结帷幕温度,避免工程事故的发生,为今后太原地区的同类工程提供依据。

1 工程概况

太原地铁2号线双塔西街站～大南门站区间采用盾构法施工,区间全长1 098.933 m。区间隧道顶覆土厚度约10.8～24.2 m。地层剖面图如图1所示。区间采用一台太原重工生产制造的土压平衡盾构机施工,盾构刀盘开挖直径6.46 m,主机总长8.358 m。盾构隧道穿越地层为黏质粉土、粉细砂、局部含有中砂和砾砂。在工程风险中富水粉细砂位于工程地质风险第一位。综合现场地质特点以及具体施工条件最终决定采用垂直冻结法进行该盾构始发端加固。采用冻结法进行加固就是以盾构出洞方向为轴心,将土体临时加固为长12 m,宽3 m,高22 m的冻土墙,达到承受一定水土压力,保证盾构顺利通过洞门的作用。

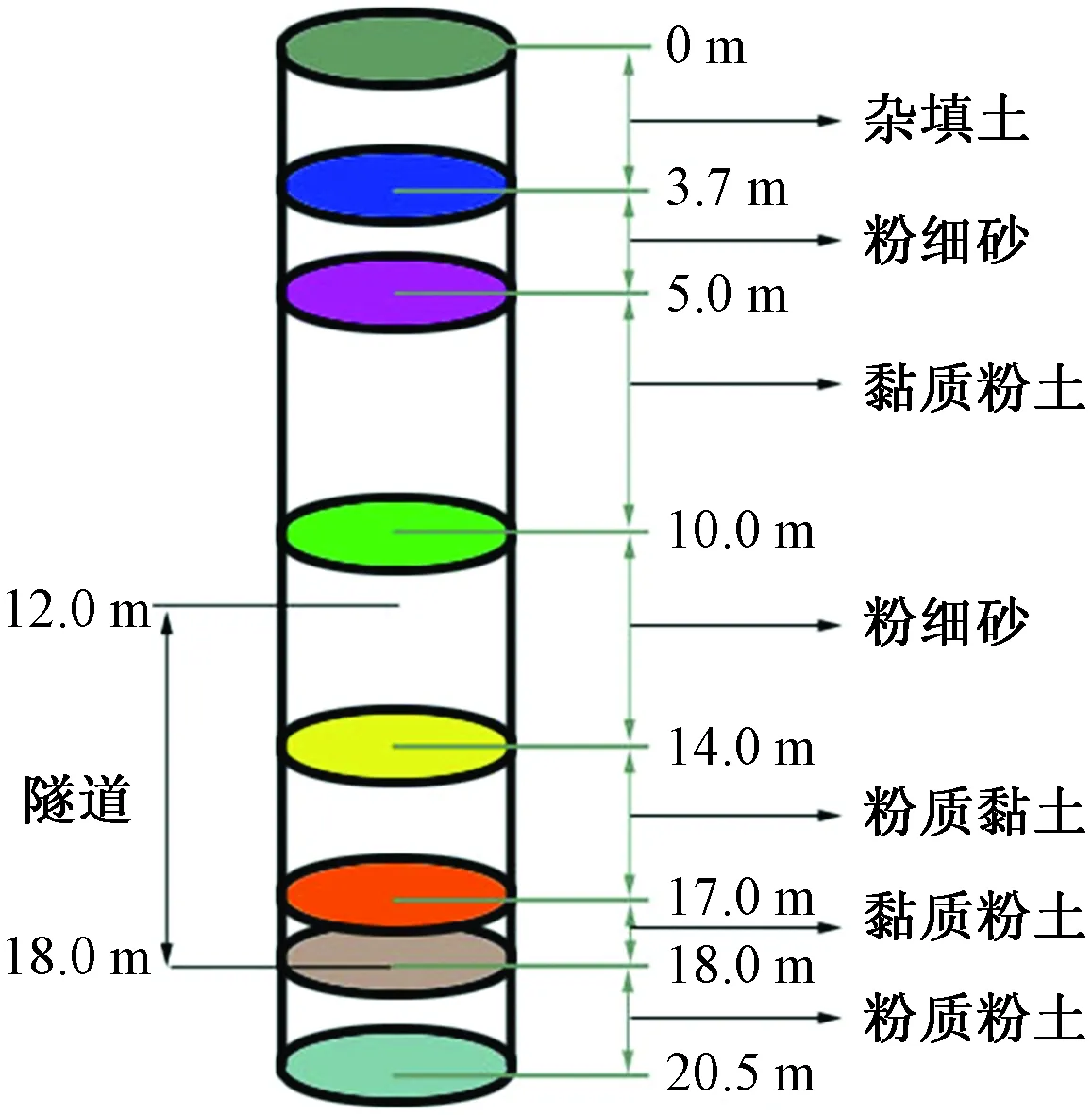
图1 土层分布柱状图Fig.1 Histogram of distribution of soil compositions

2 现场冻结方案设计

2.1 冻结施工方案

冻结施工能否取得较好的冻结效果取决于冻结孔的合理布置方案,其工作极为重要,考虑工程水文地质条件及盾构施工条件,采取三排垂直孔全断面冻结加固方式。洞门共布置45个冻结孔,梅花布置。第一排孔数16个,距槽壁0.4 m,孔间距0.8 m；第二排孔数15个,孔间距0.8 m,与第一排排距为0.8 m；第三排孔数14个,孔间距0.8 m,与第二排排距为0.8 m。冻结孔深度约为21.6 m。冻结管的实际位置如图2所示。

2.2 测温孔布置

为了很好地监测冻结帷幕在冻结过程中的发展情况,在垂直冻结区域内设置六个测温孔,其中测温孔C1和测温孔C4位于第一排冻结孔与地连墙之间,测温孔C2与测温孔C5位于第一排冻结孔与第二排冻结孔之间,测温孔C3与测温孔C6位于第二排冻结孔与第三排冻结孔之间,每个测温孔均设置6个测点,分别位于地表以下6.6、9.6、12.6、15.6、18.6、21.6 m,测温孔平面布置图如图2所示。

图2 冻结孔与测温孔平面位置图Fig.2 Location of frozen hole and temperature hole

2.3 制冷设计

南内环街站～双塔西街站盾构冻结帷幕交圈时间为15～20 d,积极冻结时间为21 d。积极冻结期内,需要通过测温管测得土体温度,以此为依据可以判断出冻结帷幕是否达到设计要求。这一过程的目的是为了提高土体的强度,只有形成一定厚度的冻结帷幕,才可以进行下一道工艺,以确保后期开挖的顺利进行,如果没有达到设计要求,则需要延长积极冻结的时间。

3 数值计算分析

3.1 建立温度场计算模型

室内模型试验作为一种有效的技术手段,国内外学者已经做了大量的研究,但是绝大多数的模型试验存在一定局限性:仅仅是针对某个局部进行的模拟,而对整体模型的试验研究较少,并且由于体积的缩小,所带来的误差对工程分析也是不利的。因此,进行数值模拟研究十分有必要,通过模拟和实测数据相比较的方法可以提高数值模拟的合理性和可靠性,为后期的工程施工提供一定的参考。

3.2 基本假定

建立模型的基本假定如下:①所要研究的地层为水平分布,且其材料为单一均质、热各向同性体；②土体的初始温度场均匀分布,地层初始温度为25 ℃；③忽略水分迁移的影响；④土体在温度低于-1 ℃时开始冻结,达到-10 ℃时形成稳定的冻结土；⑤为了方便计算以及考虑最不利的因素,所有土层采用传热最差的粉细砂层。

3.3 计算几何模型和参数选取

数值模拟模型采用摩尔-库仑弹塑性模型和均质热导模型,网格划分如图3所示。每米冻结管的吸热功率为-17 W/m,冻土的导热系数为1.5 W/(m·℃),冻胀率为-5×10-5/℃,冻土比热为500 J/(Kg·℃)。将盐水温度作为节点荷载考虑,即温度载荷直接施加在相对应的冻结轴面节点上,固定约束模型外边界,并在模型外边界设置为绝热条件。模拟过程设定冻结时间为37 d,冻结天数采用solve age命令给定具体值改变时间步数[13]。

图3 模型网格划分Fig.3 Gridding of the model

数值模拟首先应该确立一个合理的分析范围,随后建立相关的地质模型,通过施加初始地应力以及进行边界约束,计算达到一个平衡的状态,这一过程是为了建立与真实背景接近的地质稳态模型。对冻结管的模拟是通过温度模式下的点热源填充冻结管进行的,将其发热功率设定为负值,即吸热状态。按照设定的位置和角度准确定位冻结管,冻结时间也按照预计时间进行设定,温度计算步为主步,静力计算为从步,通俗来说,主步每计算一步,从步会计算若干步直至达到平衡状态。

3.4 计算结果与分析

冻结温度场的变化情况如图4所示,从模拟的结果来看,在冻结10 d时,冻结帷幕的最低温度已经降至-16 ℃,冻结20 d后,最低温度达到-23 ℃,冻结25 d时,最低温度降至-28 ℃。根据温度云图显示,随着冻结时间的增长,冻结管周围形成一个个冻结圆柱,相邻的冻结圆柱慢慢连接交圈形成具有一定厚度的冻结帷幕,随着冻结帷幕厚度的增加,强度也随之增强。由图4(b)可知,冻结20 d后冻结帷幕已经基本完成交圈,并且形成一定厚度的冻结帷幕以抵抗外界的水土压力。

图4 温度云图Fig.4 Temperature clouds

4 温度场现场实测分析

通过实测可以实时掌握冻结加固过程中加固体不同部位的温度变化情况,以及去回路盐水温度及温差变化,在这些数据的支撑下可以推算出冻结帷幕厚度及平均温度,继而反馈有效的信息来指导施工,帮助准确推断洞门槽壁凿除和盾构始发的时机,确保施工安全[14-15]。

4.1 干管盐水温度监测

冷冻机开机之后每日记录干管去回路盐水温度,直到冻结第37 d结束。干管去路和回路盐水温度随冻结天数变化曲线如图5所示。

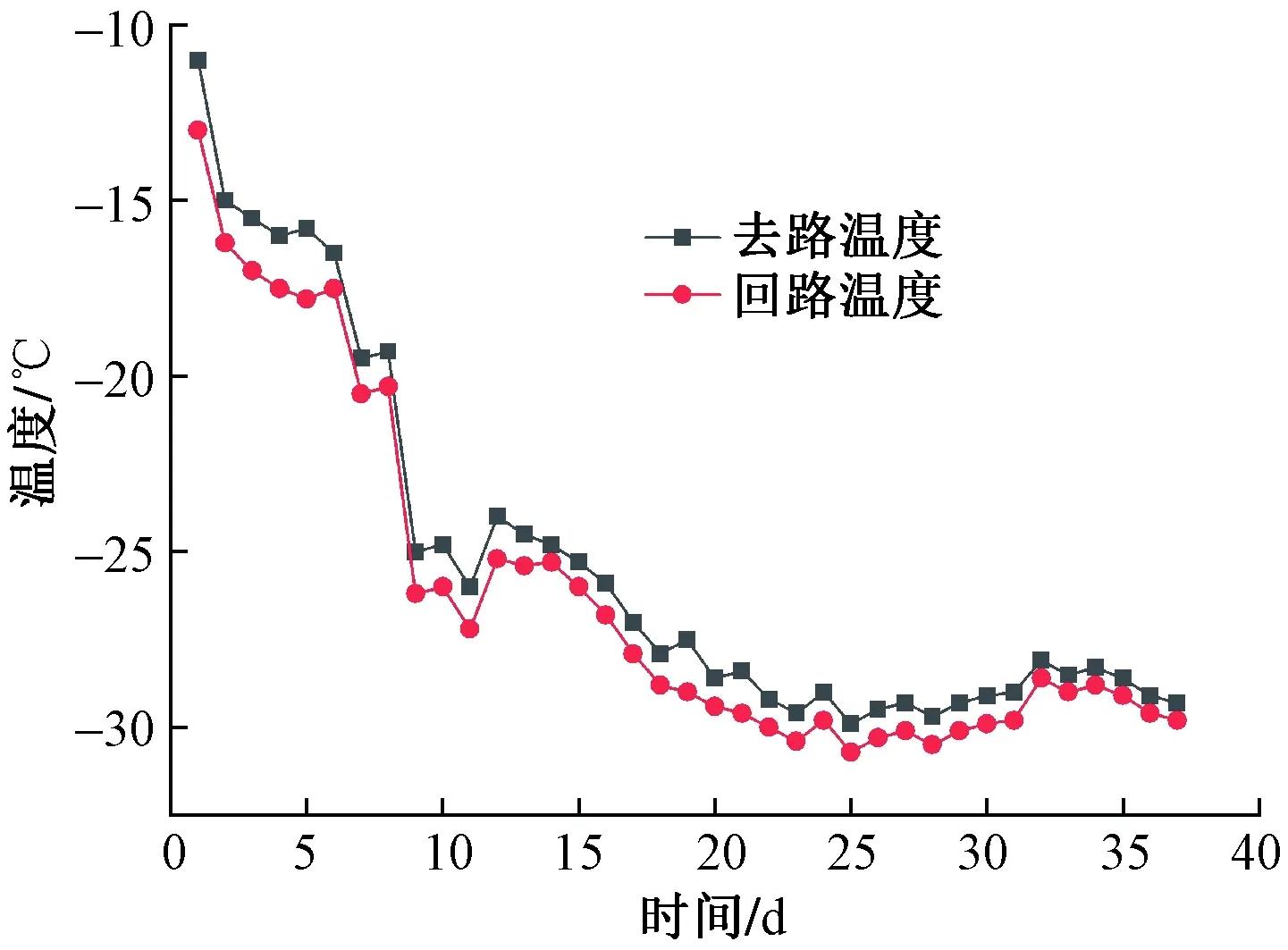
图5 干管盐水时间温度曲线Fig.5 Time-temperature curves of main pipes

由图可知:在积极冻结期后期冻结系统盐水温度基本稳定在-28 ℃以下,去回路的温差保持在0.8 ℃左右,差值符合冻结设计要求(≤1.5 ℃)。

4.2 测温孔监测分析

从冻结开机之日对土体温度进行监测,每日监测一次。将实测数据导入origin软件进行处理,得到各测温孔在不同深度处的温度变化规律(图6)。由图6可知各测温孔温度变化规律相似:在开始冻结之前,地层的初始温度是一个定值。冻结开始之后,土体的温度会在短时间内迅速的下降到0 ℃附近,这是由于在冻结最开始的时候土体的温度和冻结管内流动的低温盐水温差较大,因此产生剧烈的热交换,带走大量的热能,促使温度下降较为迅速。距离冻结管越近,土层的温度就越低。在此之后土中的水产生相变,其释放的潜热减慢了土体温度下降,致使温度下降变得平缓,而后随着相变潜热的减小,以及盐水不停给土体提供冷量,温度继续迅速下降,各冻结圆柱逐渐交圈形成了完整的垂直冻结帷幕,温度最终趋于稳定。

图7 各测温孔同一深度处时间-温度曲线Fig.7 Time-temperature curves at the same depth of each thermometer hole

提取六个测温孔3测点处的温度变化规律进行比较。由图7可知，在变化趋势上各测温孔表现基本一致,都是随着冻结天数的增加,温度也在逐渐降低。而在最低温度以及降温速度方面,各测温孔表现具有差异性,可分为两类讨论,第一类为靠近地连墙的部分(C1、C2、C4、C5),第二类为远离地连墙的部分(C3、C6),可以发现由于靠近地连墙一侧的混凝土导热系数要低于土层的导热系数,因此远离地连墙一侧的最终稳定温度(最低温度-13 ℃)明显高于靠近地连墙一侧的温度(最低温度-28 ℃),且第一类测点降温速度要明显高于第二类测点。

为验证冻结温度场计算模型的正确性,取冻结温度场计算模型中代表点1～6跟实测温度点C1～6的温度变化曲线进行对比,如图8所示。

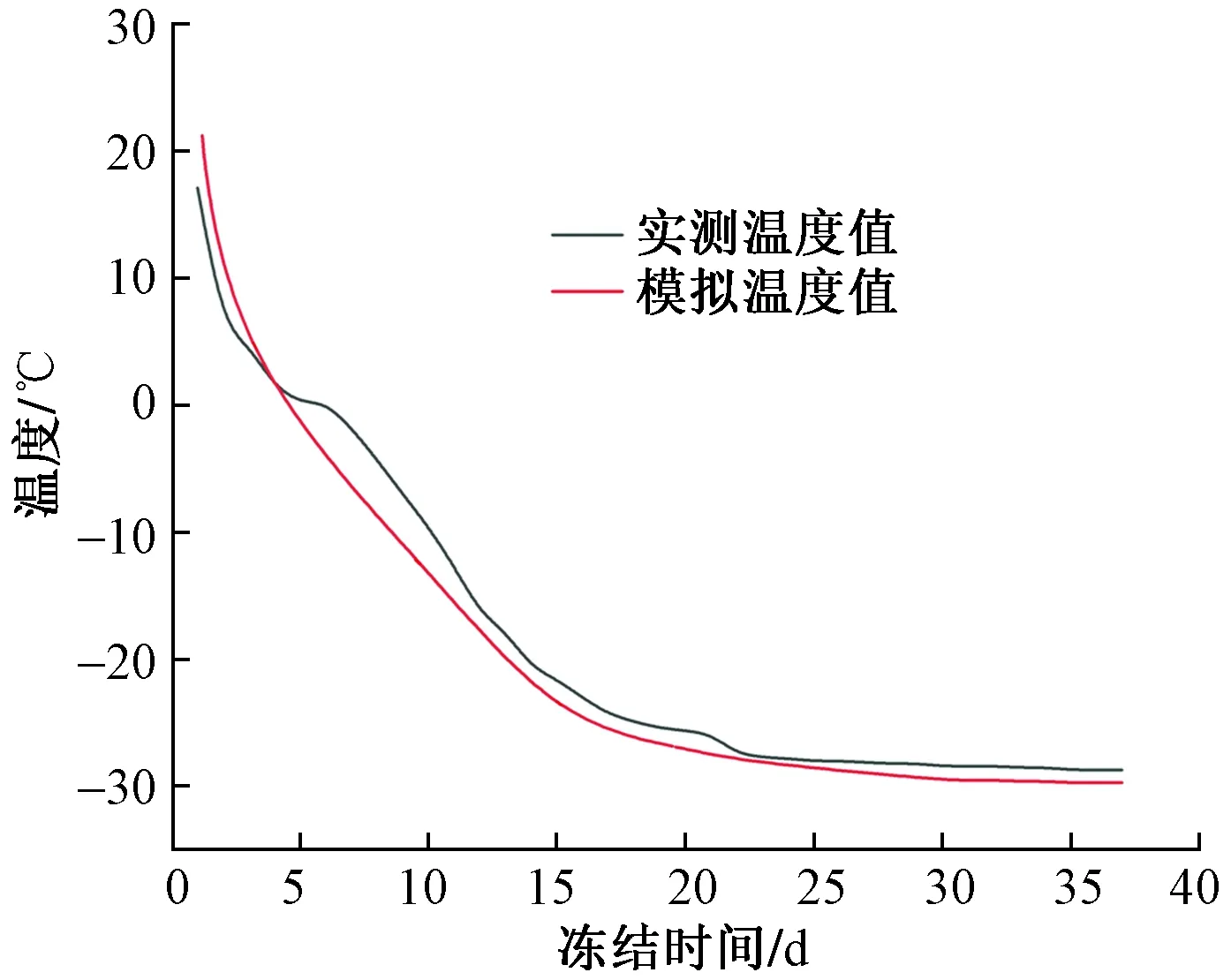
图8 实测数据和模拟数据对比Fig.8 Comparision of measured data and simulated data

由图8可知，两条曲线均呈现“阶梯”状,实测温度值比模拟温度值略高,实测的曲线有高低起伏现象,模拟的曲线则相对较为平滑,但是所呈现出的温度变化规律基本一致,数值比较接近。造成这种现象的原因可能是,忽略了测温孔与冻结管之间偏斜产生的影响,并且有限元分析过程中假设较为理想化,土体为各向同性的均质材料,未考虑土中水的存在,忽略了水分迁移的作用,实际冻结过程中土中会有空隙,阻碍冷量的传递,因此模拟值与实测值会出现一定的偏差。总起来说,数值模拟的模型以及各参数较为准确,利用有限元软件模拟温度场的发展情况是可行的,今后类似工程可采用有限元法对温度场发展进行预测并且对交圈时间进行准确的判断,提高工程效益。

4.3 冻结圆柱半径及冻结帷幕厚度计算

通过推算冻结圆柱的半径、冻结帷幕的厚度和冻结帷幕的平均温度,可以有助于掌握垂直冻结加固范围内的温度场分布,以此为依据判断洞门槽壁凿除以及盾构机始发的时间。冻结圆柱的半径由成冰公式[16]得出:

(1)

式(1)中：r2为冻结圆柱的半径,m；t1为盐水回路温度, ℃；r为测温孔与冻结管之间的距离,m；t为测温孔温度, ℃；r1为冻结管的内半径,m。

由于C3和C6测温孔温度下降异常,因此不宜作为判断冻结帷幕形成的依据。C1、C2、C4、C5测温孔温度下降正常,可以作为计算的依据。依据最不利原则,C1、C2、C4、C5中测温孔数据最高温度为C5测温孔测点深度为6.6 m处,第21天为-8.5 ℃,将该点的温度取值代入到式(1)中,可以求得,最小冻结圆柱的半径为0.938 m,如果不考虑冻结孔与测温孔之间的偏斜问题,在理想状态下冻结帷幕的交圈如图9所示,根据此示意图可以确定冻结帷幕的实际厚度为3.138 m(将地下连续墙的部分扣除后的实际厚度),大于设计冻结帷幕厚度3 m,证明满足设计要求。

图9 冻结帷幕交圈示意图Fig.9 Schematic of the freezing wall composed of intersecting circle

4.4 冻结帷幕的平均温度计算

在判别冻结帷幕是否具有足够强度的时候,冻结帷幕的平均温度是一项十分重要的指标,其正确与否会直接影响对冻结法施工进程的控制。陈文豹等[16]在对煤矿井筒进行多次温度实测的基础上,总结得出了单排管的冻结帷幕平均温度计算公式,目前在中国工程界多采用此公式进行计算:

(2)

tc=tcp+0.25tn

(3)

式中：tcp为按零度边界线计算的冻结帷幕的平均温度, ℃；th为冻结管的外壁温度, ℃；l为冻结管的间距,m；E为冻结帷幕的厚度,m；tc为冻结帷幕的平均温度, ℃；tn为测点温度, ℃。

计算得出冻结帷幕的平均温度为-11.79 ℃,小于设计冻结帷幕平均温度(-10 ℃),满足设计所需要求。

5 结论

(1)在验证冻结实测方案时,通过布设测温孔监测不同部位测点温度和全过程记录总去总回盐水温度这一方法是合理并且可行的。

(2)根据实时监测的数据,在第37 d时,总去路盐水温度为-29.8 ℃,总回路盐水温度为-29.3 ℃,温差为0.5 ℃,温差在设计要求范围之内(≤1.5 ℃)；通过计算得出冻结帷幕厚度为3.138 m,满足设计要求(≥3 m)；计算得冻结帷幕平均温度为-11.79 ℃,达到设计要求(≤-10 ℃)，证明在该工程采取冻结法施工冻结效果良好,已经达到设计要求的加固强度,可以进行下一步的洞门槽壁凿除以及盾构始发工作。

(3)本次工程案例采取的垂直冻结施工方案以及全面实时监测方案可以为太原地区其他盾构端头加固工程的设计与施工提供借鉴和参考。

(4)在进行冻结模拟时,仅仅采用温度场与应力场耦合的方法,在实际工程中土体中含有流动的地下水,会影响温度场的分布,因此在以后的研究中应该考虑水分场的作用。