基于灰色关联度-主成分法的高速公路雾灾评估模型——以沿海高速江苏段为例

周林义, 钱 玮, 崔海蓉， 王宏斌

(1.中国气象局交通气象重点开放实验室, 江苏省气象科学研究所,南京 210008；2.南京信息工程大学管理工程学院, 南京 210044)

伴随着中国道路通车里程、机动车和驾驶人员数量、道路交通运营量的大幅增长,公路交通安全已成为政府和公众最关心的重要问题之一。气象条件是影响公路交通运输安全的重要因素[1]。大雾、雨雪冰冻、暴雨等恶劣天气不仅会造成交通拥堵、瘫痪,而且极易引发交通事故,造成社会经济损失甚至人员伤亡[2]。近年来,由气象灾害引发的交通事故具有明显增大的趋势,然而,有关交通气象灾害评估的研究却鲜有人涉及。虽然公众经常从媒体报道或官方统计数字中了解到交通气象灾害造成的直接经济损失和人员伤亡数字,但是,这些数字仅仅部分反映了灾害影响,人们缺乏对灾害等级的划分以及对灾害损失程度的精确认识。因此,气象灾害灾情评估和风险管理逐步成为研究的重点和热点问题[3]。

近年来,江苏省高速公路建设可谓日新月异,自从1996年沪宁高速公路建成通车以来,江苏省高速公路建设投入不断加大,通车里程和密度不断提高,截至2018年底,江苏省高速公路总里程已经突破4 000 km。在江苏省高速公路大发展阶段,高速公路事故频发以及事故造成的严重程度与日俱增,其中恶劣天气是造成事故的重要原因之一,尤其以雾灾为最,每年第一和第四季度更是雾情高发季节。大雾对江苏省高速公路安全管理构成了严峻挑战。

在此将对高速公路雾灾灾情评估模型展开研究,并以沿海高速江苏路段进行实例分析,所以给出的模型及方法不仅限于沿海高速江苏路段,对于其他大雾灾情高发的高速公路段同样适用。

有关高速公路气象灾害方面的研究近年来逐渐增多,但基本都是针对高速公路气象灾害风险评估或预警的,例如柳艳香等[4]对各种高速公路气象灾害风险评估方法进行了比较和分析。顾婷婷等[5]考虑高速公路的自然地理环境特征,从危险性、暴露度、脆弱性3个方面出发,建立了高速公路暴雨灾害风险评估指标集。张金满等[6]构建了雾天高速公路风险预警指标体系,并针对京沪、黄石高速河北段进行实证检验。而专门针对高速公路气象灾害灾情评估的文献目前仅有李岚等[7]运用灰色关联度分析法对辽宁高速公路雾灾进行了评估。

关于灰色关联度分析法(grey relational analysis,GRA)近年来在各领域评估方面也是得到了众多学者的青睐,例如张娜等[8]基于GRA评价了引种郁金的质量。崔祥民[9]运用改进的GRA从价值链的角度构建了众创空间核心竞争力评价指标体系。在气象灾害评估方面,应用趋势也在逐渐加强。周伟灿等[10]将GRA应用于长江三角洲雾灾灾情的评估,认为GRA对雾灾灾情损失评估具有可行性,评估结果符合实际情况。李亚滨等[11]采用GRA进行灾害等级划分,研究暴雨灾害与气象因子之间的关系,建立了反映暴雨灾害程度的5项单指标及综合评估指数,并在此基础上建立了评估和预评估模型。

尽管灰色关联度分析法得到了非常广泛的应用,但是该方法在最后计算关联系数综合指标时,通常假设各指标的关联系数具有相等权重,从而对各指标取算数平均值,与实际存在偏差。因此,针对此现象,将灰色关联度分析法与主成分分析法(principal component analysis,PCA)巧妙结合,即在灰色关联度分析法基础上,首次采用大量历史数据,运用主成分分析法计算各指标的关联系数权重,通过各指标的加权平均值获得更加符合实际的关联系数评价值。

1 高速公路雾灾评估模型

1.1 高速公路雾灾评估指标及数据资料说明

1.1.1 高速公路雾灾评估指标

通过对现有文献的研究和梳理,并结合高速公路大雾灾害实际,选取以下5个指标作为高速公路雾灾评估指标:X1为大雾持续时间min；X2为大雾出现时最低能见度m；X3为高速公路发生交通事故数量；X4为高速公路交通事故受伤人数；X5为高速公路交通事故死亡人数。

1.1.2 数据资料说明

选取江苏省沿海高速作为实例分析对象,即沈阳至海口高速公路江苏段,路线全长403.28 km。研究所涉及的气象资料来源于江苏省气象局,高速公路交通事故资料来源于江苏沿海高速公路管理有限公司,数据的时间跨度为2010年1月1日～2014年12月31日。

由于主要研究内容为高速公路雾灾评估,所以需要将数据资料中的非雾天气排除掉。数据中存在对天气现象描述模糊的情况,如“雨雪”,“雨雾”、“烟雾”等,根据文献[2]的处理方法,再结合高速公路段的气温、相对湿度等当时采集的实况数据,将“雨雪”纳入雪、 “雨雾”纳入雾、“烟雾”纳入烟幕等。此外,在数据整理时还发现,由于沿海高速江苏段路线较长,不同路段大雾持续时间及出现时的最低能见度有显著差异,所以考虑对高速公路分路段采集数据。因大雾出现时最低能见度数据缺失,这里采用高速公路分路段交通管制等级作为大雾出现时最低能见度的替代数据,具体路段划分根据江苏省高速公路管理局实际桩号划分为依据。

关于高速路分段管制,通常是一条管制记录代表某一路段的一次管制。交通管制等级一般分为特级、一级、二级、三级及其他(临时管制) 。针对雾来说,主要根据大雾出现时的最低能见度来指定管制等级,所以用交通管制等级来代替大雾最低能见度是合理的,并且高速路分段采集数据也解决了因高速路程过长所产生的差异性,从而使分析更有针对性。

以上处理完毕后,得到的数据总量为1 458组。

1.2 高速公路雾灾评估模型构建

1.2.1 基于GRA的雾灾评估模型

灰色关联度分析法是一种多因素统计分析的方法。它以各因素的样本数据为依据, 用灰色关联度来描述因素间关系的强弱、大小和次序, 若样本数据反映出的两因素之间的变化趋势(方向、大小和速度等)基本一致, 则它们之间的关联度较大, 反之关联度较小。与传统多因素分析方法相比较, 灰色关联度分析法对数据的要求较低且计算量较小[12], 因此该方法被广泛应用到社会和自然科学的各个领域, 尤其在灾情评估和经济领域均取得了很好的应用效果。

首先对所有评估指标进行无量纲化处理,以使不同标准的雾灾等级划分标准取得统一[13]。为方便后续运用灰色关联度分析法,其中交通管制等级这一指标采用如表1所示的转换方法。

表1 大雾出现时交通管制等级无量纲转换

其余四个指标则采用各指标除以其在所选时间跨度中(2010年1月1日—2014年12月31日)单次案例出现的最大值所得的商作为最终无量纲化处理结果,例如2012年6月6日在沿海高速江苏路段(G15),桩号为K851-K1088发生的一次雾灾,相关指标对应的数据为:大雾持续时间系数=实际大雾持续时间/单次案例大雾持续最长时间=153 min/1 610 min≈0.095 0；高速公路交通管制等级系数为0.4；高速公路交通事故发生数量系数=实际发生数量/单次案例发生最多数量=1/7≈0.142 9；高速公路交通事故受伤人数=实际受伤人数/单次案例受伤最多人数=1/35≈0.028 6；高速公路交通事故死亡人数=实际死亡人数/单次案例死亡最多人数=0/12=0。

根据GRA原理,需要确定参考序列(母序列)和比较序列(子序列)。这里以各指标出现的最大值所组成的序列为参考序列,即X0(tk)={1,1,1,1,1},表示出现的最严重的灾情。以实际单次大雾灾害中出现的数据序列作为比较序列,即待评估序列,例如2012年6月6日发生的这次雾灾,比较序列为Xj(tk)={0.095 0,0.4,0.142 9,0.028 6,0}。

计算灰色关联系数:

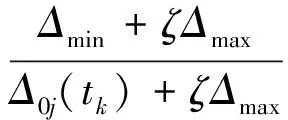
{0.782 9,1,0.736 9,0.747 6,0.733 3}

(1)

式(1)中,Δmin为X0与Xj各指标的最小绝对差值,此例中取值为0.6；Δmax为X0与Xj各指标的最大绝对差值,此例中取值为1；Δ0j(tk)(k=1,2,…,n)=|X0(tk)-Xj(tk)|；ζ为分辨系数,一般事先给定,这里借鉴大多数文献的做法,取ζ=0.5。

关联系数ξ0j(tk)反映了参考序列与比较序列之间的远近程度,通常关联系数各指标数值越大,说明与最严重的灾情越接近,灾情也越严重。反之亦然。但关联系数只是反映了各指标之间的分散关联程度,而实际通常根据总体评估一次大雾的灾情情况,所以一般的灰色关联度假设各指标的权重相等,对各指标取算数平均值,即

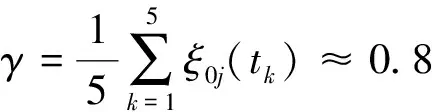
(2)

根据文献[14]给出的关联度取值与灾害等级划分之间的关系(表2),可以确定,2012年6月6日沿海高速江苏路段(G15),桩号为K851-K1088的此次雾灾灾害等级为Ⅰ特别重大。很明显各指标取算术平均值高估了此次雾灾的评级。

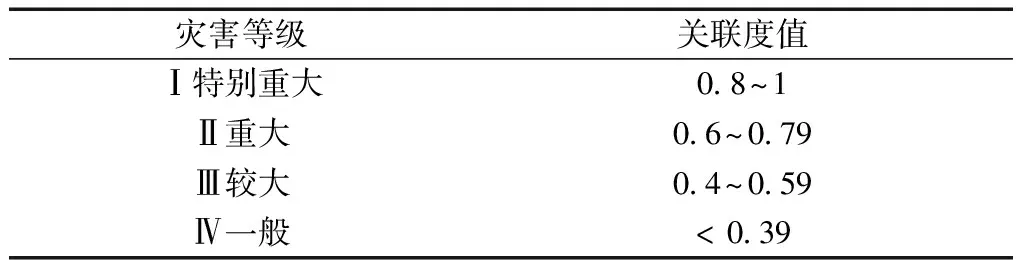
表2 灰色关联度取值与大雾灾害等级对应关系

1.2.2 基于GRA-PCA的雾灾评估模型

主成分分析法(principal component analysis,PCA)的主要作用是降维,减少分析的指标数。原始指标之间通常具有一定的共线性,信息的重叠度很高,所以可以通过线性组合的方式提取绝大部分信息,在只损耗少量信息的前提下实现降维的目的。在此,除了上述目的以外,还为了能够客观给出各个指标的权重,以规避后续建模过程中,因指标权重过于均衡和主观所造成的评估偏差。

在此之前,首先需要利用KMO和Bartlett球检验确定主成分分析法是否适用于所选取的指标。

如表3所示,KMO(Kaiser-Meyer-Olkin)用于检验样本的偏相关性,其值等于0.803 0,大于0.7,说明适合做主成分分析。Bartlett球检验用于表示因子是否独立提供一些信息,P=0.000<0.05,拒绝原假设,说明各指标之间有一定相关性,主成分分析是有效的。综上所述,KMO和Bartlett球检验通过,可以进行主成分分析。

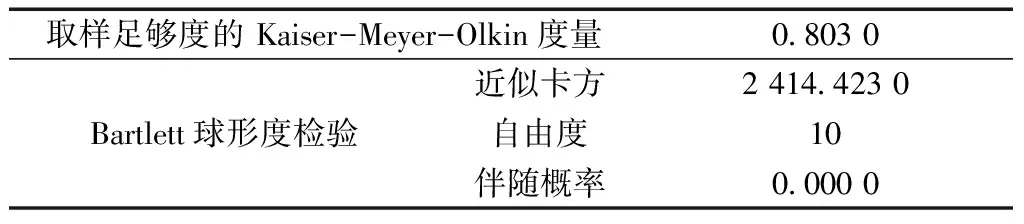
表3 KMO和Bartlett球检验

每个主成分对所有因素的解释能力可以通过其对应的解释总方差占比来衡量。由解释的总方差(表4)可知,旋转平方和载入中累积方差贡献率高达81.988%,即提取出的3个主成分能够概括原来80%以上的信息,主成分分析效果较好。

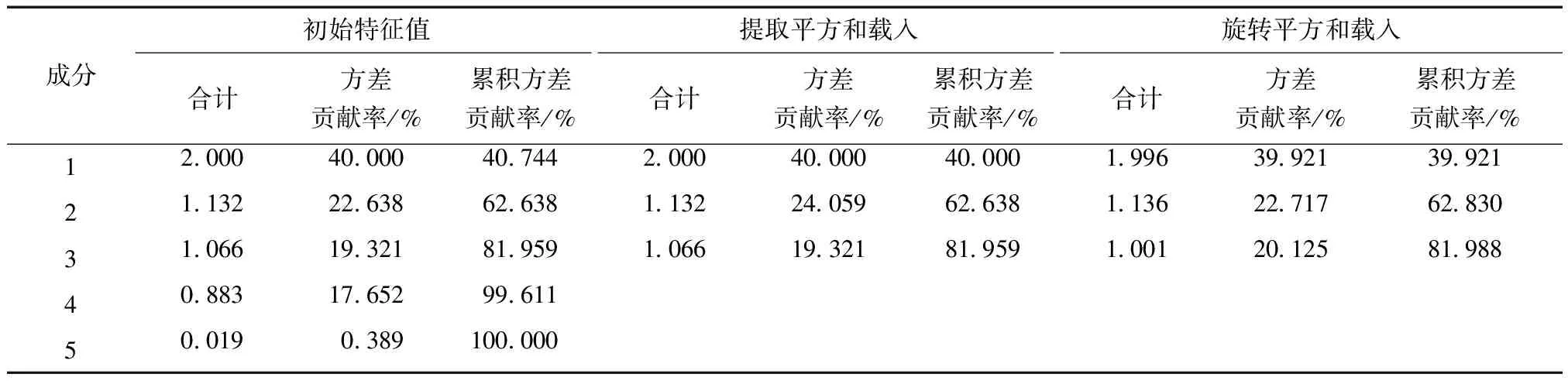
表4 方差和累积方差贡献率

运用软件SPSS 20.0计算输出3个主成分的得分公式为

F1=-0.053ξ0j(t1)+0.075ξ0j(t2)+0.336ξ0j(t3)+

0.496ξ0j(t4)-0.034ξ0j(t5)

(3)

F2=0.441ξ0j(t1)+0.325ξ0j(t2)+0.011ξ0j(t3)-

0.102ξ0j(t4)-0.204ξ0j(t5)

(4)

F3=-0.068ξ0j(t1)+0.242ξ0j(t2)+0.003ξ0j(t3)+

0.083ξ0j(t4)+0.004ξ0j(t5)

(5)

将2012年6月6日所计算的灰色关联系数值ξ0j(tk)={0.782 9,1,0.736 9,0.747 6,0.733 3}分别代入式(3)～式(5),得出F1=0.628 8,F2=0.452 5,F3=0.256 0,再将各个特征根除以3个特征根之和得到各主成分的权重,主成分总得分F等于各主成分的权重乘以得分之和,公式如下:

γ=(39.921/81.988)F1+(22.717/81.988)F2+(20.125/81.988)F3

(6)

由此得出2012年6月6日的灾害评级总得分γ=0.431 6。根据表2判断,此次雾灾的评级为Ⅲ较大,与式(2)计算的结果相比,显然更加合理。

2 沿海高速江苏段雾灾评估实证分析

根据以上陈述的高速公路雾灾评估方法,现对沿海高速江苏路段1 458组数据进行雾灾评估,首先分别对相关数据进行无量纲化处理,然后运用GRA-PCA模型对各路段和时间段的雾灾进行评估,评估结果详见表5。表6给出16例部分桩号的评估结果。

根据表5、表6,总体来看,沿海高速江苏路段雾灾损失程度得到了很好的控制,其中大部分情况下处于Ⅳ一般等级,占比95.47%,少部分为Ⅰ特别重大和Ⅱ重大,分别占比0.14%和0.75%。说明近几年,江苏省交通厅在雾灾预警和应急方面所作的大量工作起到了较为显著的成效,但仍有可改进的空间,以杜绝Ⅰ特别重大和Ⅱ重大情况的发生。

表5 沿海高速江苏路段雾灾评估结果

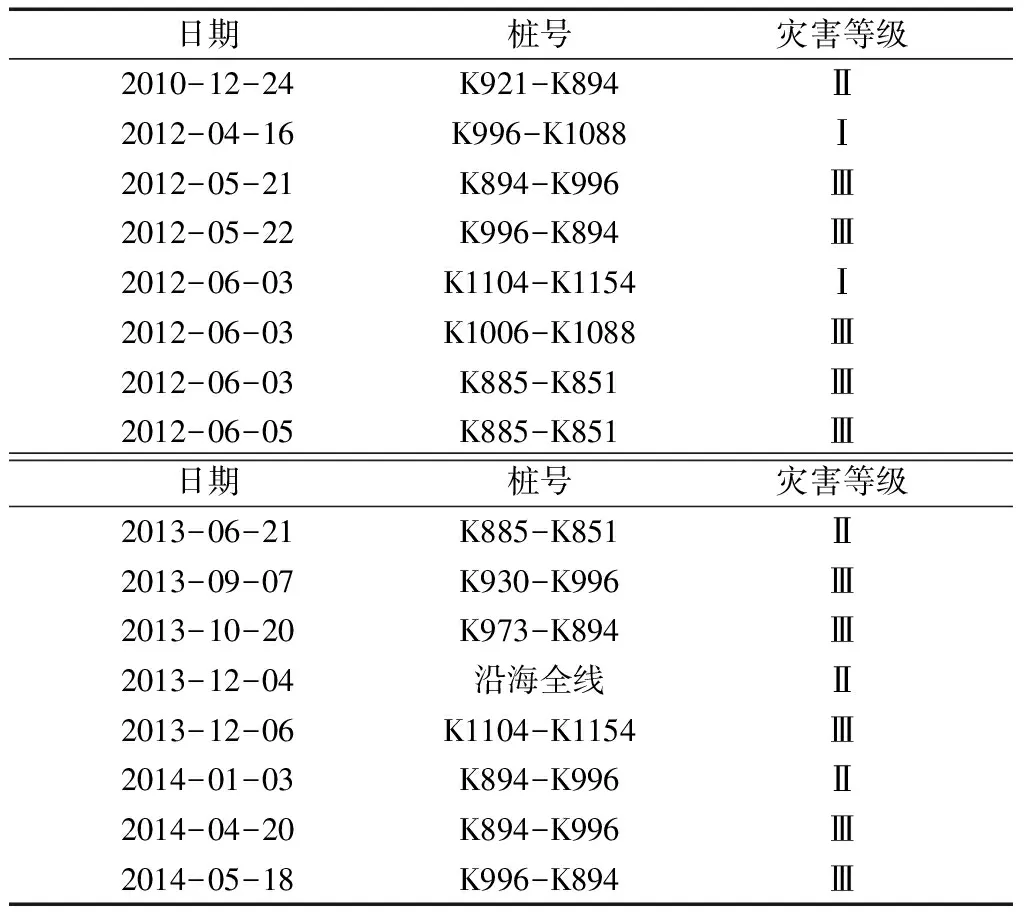
表6 部分桩号雾灾评估结果

3 结论

有效的雾灾灾情评估不仅为人们提供对灾害损失程度的精确认识,也为相关管理部门提供可参考的依据。据交通及气象部门统计,大雾是影响高速公路安全行使最常见的气象灾害之一。然而,现有文献中较多是对高速公路大雾天气的成因、大雾的预报及预警方面的研究,对雾灾灾情评估的研究少之又少。在此不仅建立了高速公路雾灾评估指标体系,同时还构建了GRA-PCA高速公路雾灾灾情评估模型,将灰色关联度与主成分分析法巧妙地结合在一起,并以沿海高速江苏路段为例,详细阐述了模型的运作过程,同时对沿海高速江苏路段雾灾灾情情况进行实证分析,验证了模型的有效性和合理性。

后续研究将集中在采用更多省份的数据进一步检验模型的有效性,同时结合高速公路雾灾预警,研究预警对降低雾灾灾情程度的作用机制。