基于最小体积封闭椭球算法的多段水力压裂改造体积估算
2020-02-24王旭林桂志先易娟子
王旭林, 桂志先, 王 鹏*, 易娟子
(1.长江大学非常规油气湖北省协同创新中心, 油气资源与勘探技术教育部重点实验室,武汉 430100;2.中国石油天然气股份有限公司西南油气田分公司重庆气矿,重庆 400021)
页岩油气作为一种新型能源,因其资源十分丰富,越来越被人们所重视。页岩油气储层具有低孔隙度、低连通性、低渗透率的物性特性,通常需要采取增产措施来改善其岩石物理特性[1]。由于页岩油气藏的特殊性,在勘探开发中影响页岩油气井产能的因素有很多。研究表明,储层压裂改造体积是影响页岩油气藏生产效果的关键因素之一[2-3]。前人研究发现被压裂改造油气藏的生产力与被压裂改造体积正相关,改造的体积越大,其相应的增产效果越明显[4-5]。因此对压裂改造体积(stimulated reservior volume,SRV)的准确估算已经成为页岩压裂研究领域的重难点问题。前人分别采用通道长度与通道宽度来表征裂缝扩展的长度和宽度,水平井长度表征SRV[6]。上述理论模型方法均采用立方体来拟合SRV,但包括较多的无效范围,所以拟合效果较为粗略[7]。温庆志等[8]结合压裂缝网络形态,通过研究均质地下储层中主裂缝周边的应力场发现,地应力场方向改变的区域形成缝网,缝网区域大致为椭球体,因此可以近似地认为压裂形成的缝网为椭球体。同时,微震事件的空间展布特征也被用来估算SRV[9]。因此,可将压裂形成的微震事件的空间展布近似处理为椭球体,来估算储层压裂改造体积。邵媛媛等[7]基于地震事件震源点将压裂改造体积拟合成椭球体,建立了储层改造体积最小椭球模型,通过对比其他方法得出最小体积椭球模型获得了更为详细的SRV几何结构。但上述改进方法只能得出储层改造体积的近似形状与各种参数对改造体积估算的影响,尚未给出比较完整的椭球体积估算方法。在实际生产过程中,多段压裂施工作业会出现各段压裂裂缝网络存在交错叠合的情况,并且由于多种因素的影响,单段压裂裂缝可能会呈现出较为复杂的网络形态,即表现为微震事件的空间展布形态复杂。因此,使用单一的模型很难解决上述复杂的压裂裂缝网络的压裂改造体积的估算。
本文针对实际压裂改造过程中存在的多段压裂改造体积存在重叠和单段压裂形成的复杂裂缝网络两类情况进行分析,估算对应的压裂改造体积。对多段压裂体积重叠的情况,首先利用DBSCAN(density based spatial clustering of application with noise)算法对各段微震事件分别进行处理,消除异常的微震事件,再利用MVEE算法估算出各段微震事件对应的最小体积封闭椭球体,并获得椭球体的相关参数(椭球体中心点、特征值和特征向量等),然后对压裂作业区进行网格化,结合各个椭球体参数,使用仿射变换判断各个网格点与每个椭球体的归属关系,进而统计出各段压裂改造体积间的重叠部分;针对单段压裂形成的复杂裂缝网络形态的情况,采用DBSCAN算法对微震事件进行分组,将复杂的微震事件展布转化为多个展布相对简单的分组,以各个分组的微震事件为基础,计算对应的最小体积椭球体,并消除各个椭球体间的重叠部分,进而估算出单段压裂的整体改造体积。本文还利用两组实际微震监测数据,对上述两类情况进行分析与估算,以验证本文方法的可行性与准确性。
1 方法原理
1.1 最小体积封闭椭球
最小体积封闭椭球算法(MVEE)[10]是通过寻找一个n维最小封闭椭球以包含给定的所有点集合,并获取相应椭球的信息,如椭球轴半径、椭球中心、椭球体积等。MVEE问题在数据挖掘、模式识别等领域应用十分广泛。
任意一个椭球可表示为
E(a,A)={x∈R3|(x-a)TA(x-a)≤1}
(1)
式(1)中,a∈R3为该椭球体的中心点;A∈R3×3为对称正定矩阵,该矩阵实现椭球体向单位球体的仿射变换,矩阵A的特征值(λ1、λ2、λ3)平方根倒数分别为椭球体半轴长,即实现仿射变换的缩放处理;特征向量实现仿射变换的旋转处理。式(1)也可表示为
E=Mtranslation×Mrotation×Mscaling×C
(2)
式(2)中,Mtranslation、Mrotation和Mscaling分别为平移、旋转和缩放三种仿射变换;C为单位球体;E表示最终的椭球体。Mrotation与矩阵A的特征向量矩阵互为逆矩阵;Mtranslation由中心点a控制。
以微震事件的展布特征为基础获得的最小体积封闭椭球体的体积可表示为

(3)
求解最小体积封闭椭球问题转可化为最优化问题:
minA[-(ΔA)1/2], (x-a)TA(x-a)≤1
(4)
由于-(ΔA)1/2不是一个凸函数,所以式(4)的优化模型不是一个凸优化模型,不具备凸优化的性质。利用KY算法[11]对之进行凸优化处理,并最终实现对最小体积封闭椭球的求解,获得椭球体的中心点a与矩阵A。
1.2 DBSCAN算法
实际微震监测数据处理会受到各种因素的影响,例如速构建度模型的误差、微震事件初至信息无法准确拾取等,这些因素都会影响到最终的微震事件定位精度。同时,由于页岩储层的非均质性、天然裂缝的发育程度等因素的影响,压裂形成的裂缝结构更为复杂。因此,需要对微震事件进行适当的预处理,消除定位异常的影响,并对复杂压裂裂缝的分组处理。
DBSCAN是一种基于密度的空间聚类分析算法,能将具有足够密度的区域划分为簇,在具有噪声的空间数据中发现任意形状的簇[12]。该算法被广泛应用于各个领域的数据处理与分析,例如提高雷电定位算法的抗干扰能力[13]、数据挖掘[14]、分析电力工程数据的完整性[15]和岩石物理实验数据的处理[16]。其中,Eps和MinPts是整个算法最为关键的参数,其含义分别为单簇内样点间的最大距离(又称聚类半径)和单簇包含的最小样点数。并由此引申出核心点、直接密度可达、密度可达和密度相连等相关概念。若某个样点的Eps临域内,临近样点数大于或等于Minpts,则该样点就是核心点;若某样点到达核心点的距离小于Eps,就说明从该样点到核心点直接密度可达;对于一个样点序列,样点间依次满足直接密度可达,即直接密度可达满足传递性,则这些样点是密度可达;若两个样点对于同一样点密度可达,就认为这两个样点是密度相连[17]。
DBSCAN的处理流程可描述为:①在整个样点数据集中随机挑选出一个样点,并确保该样点为核心点;②以该样点为起点,寻找到所有密度相连的数据点,并将寻找结果建立新簇;③重新扫描样点数据集(不包括之前已有簇中的任何样点)寻找新的核心点,再重复步骤②,直到没有新的核心点为止[18]。原始样点数据集中没有被包含在任何簇中的样点就构成异常点。
对于微震事件空间展布为简单形态的情况,使用DBSCAN算法可以得到微震事件的核心区域,排除异常微震事件定位点对后续处理的影响;对于微震事件空间展布为复杂形态的情况,可结合其他信息,使用DBSCAN算法对微震事件进行分组处理,再基于这些分组数据使用MVEE算法,计算出各个分组对应的椭球体,从而估算出复杂裂缝网络对应的压裂改造体积。
1.3 重叠区域的处理
对于多段压裂改造,每段压裂形成的裂缝网络往往存在重叠,对应的各段压裂形成的微震事件在空间展布也存在彼此重叠。利用椭球体模型对单段的压裂改造范围进行描述时,可以获得该椭球体的中心点a和矩阵A;对于多段压裂的处理,可以得到一系列的中心点(a1,a2,…,an)和矩阵(A1,A2,…,An)。由于各段压裂形成的微震事件在空间中可能会彼此重叠,以微震事件空间展布特征为基础求得的椭球体也会出现重叠。为消除椭球体重叠区域对多段压裂整体压裂改造体积估算的影响,处理流程如下。
(1)对矩阵(A1,A2,…,An)进行处理,获得每个矩阵的特征值矩阵Mi_λ和特征向量矩阵Mi_v(i=1,2,…,n)。由上述分析可知,矩阵A的特征值的平方根倒数是对应椭球体的各个半轴长。将所有特征值转化为半轴长,寻找到最大半轴长Lmax。
(2)以每个椭球体中心点为中心,以Lmax为半径建立网络,并令Lstep为单个网格大小。判断各个网格点g与所有椭球体之间的归属关系:

(5)
若该网格点位于椭球体的表面,经过逆向处理后,正好位于单位球体的表面,即D到坐标原点的距离为1;若该网格点位于椭球体的内部,经过逆向处理后,也位于单位球体的内部,即D到坐标原点的距离小于1;若该网格点位于椭球体的外部,经过逆向处理后,也位于单位球体的外部,即D到坐标原点的距离大于1。将所有椭球体的相关参数均代入式(5)中,就可以判断出该网格点与所有椭球体间的归属关系:该网格点可能只归属于当前椭球体,或归属于多个椭球体,或不归属于任何椭球体。
(3)当以第一个椭球体为被分析对象时,统计只归属于第一个椭球体的网格点;再对下一个椭球体进行分析,此前已被分析处理的椭球体不再参与计算,统计出只归属于当前椭球体的网格点数;依次对所有椭球体进行处理,对每步统计出的网格点数进行累加,并换算成体积。此时获得数值就为消除重叠区域后的整体压裂改造体积。
2 实例分析
2.1 多段简单微震事件展布形态
实例数据来自重庆涪陵地区的页岩气田,为某页岩气储层的水平井压裂改造的微震监测项目。由于页岩气大规模开发的需要,对该页岩气储层实施了水平井多段水力压裂处理。该水平井井轨迹为南北向,并采用临井井中观测方式对压裂过程实施微震监测。提取三个紧邻压裂段的微震监测结果进行分析,各段微震事件数量分别为50、150和130,相应空间分布图像如图1所示。在图1中,X轴正向指向正东,Y轴正向指向正北。由各段微震事件的分布特征可见,微震事件的分布整体呈现东西向分布,与压裂井井轨迹走向(南北向)近似正交。各段的微震事件分布形态相对简单,但在各段微震事件之间存在较大程度的重叠。
首先,对这些微震事件进行分段处理,用 DBSCAN算法寻找到各段微震事件分布的核心区域,排除掉异常点。DBSCAN算法中的Eps和MinPts两个参数分别被设置为50和3,其物理意义是簇内两个临近微震事件间的最大距离是50 m和簇内的至少应包含3个微震事件。再由核心区域的微震事件结合MVEE算法,获得最小体积封闭椭球体及其相关参数,例如椭球体的中心,各个半轴长和椭球体的旋转矩阵等。各段处理结果如图2所示,以第2段为例,该段对应的椭球体主轴方向与微震事件的分布特征相一致,椭球体积大小可近似描述微震事件所占据的范围。将各段分析结果进行综合分析(图3),各个椭球体之间也存在明显重叠现象,各段计算获得的压裂改造体积之和显然不能作为整体的压裂改造体积,需对重叠区域进行剔除。
分别以各个椭球体为中心,以椭球体的最大半轴为半径建立网格,结合各个椭球体的参数,判断各个网格点的归属情况。逐个处理完所有椭球体后,就可获得重叠区域大小和整体压裂改造体积大小。如表1所示,各段压裂改造体积分别为255×104、406×104和317×104m3,直接对各段压裂改造体积求和为978×104m3,但消除重叠区域208×104m3,整体的压裂改造体积为770×104m3。若对多段压裂形成微震事件直接进行整体处理,计算获得的椭球体会包含更多的区域,造成压裂改造体积估值过大,并且椭球体主轴方向可能与压裂裂缝分布形态不一致。

表1 各段压裂改造体积及整体压裂改造体积
2.2 单段复杂微震事件展布形态
由于多种因素的影响,单段压裂可能会形成较为复杂的裂缝网络结构。与此相对应的微震事件的空间分布形态就无法由单一的椭球体来加以描述。进而应将复杂的分布形态分解为多个子区域进行处理。被分析的实测数据来另一页岩气储层的压裂改造项目,提取该项目的一个压裂井段的微震监测结果进行分析。该微震监测结果包含297个微震事件,其空间分布如图4所示。

图2 各段压裂的微震事件及其压裂有效体积Fig.2 Microseismic event distributions and stimulated reservoir volume for each hydraulic fracturing stage

图3 三段压裂微震事件及各段压裂有效体积Fig.3 Microseismic event distributions and stimulated reservoir volume of three stages
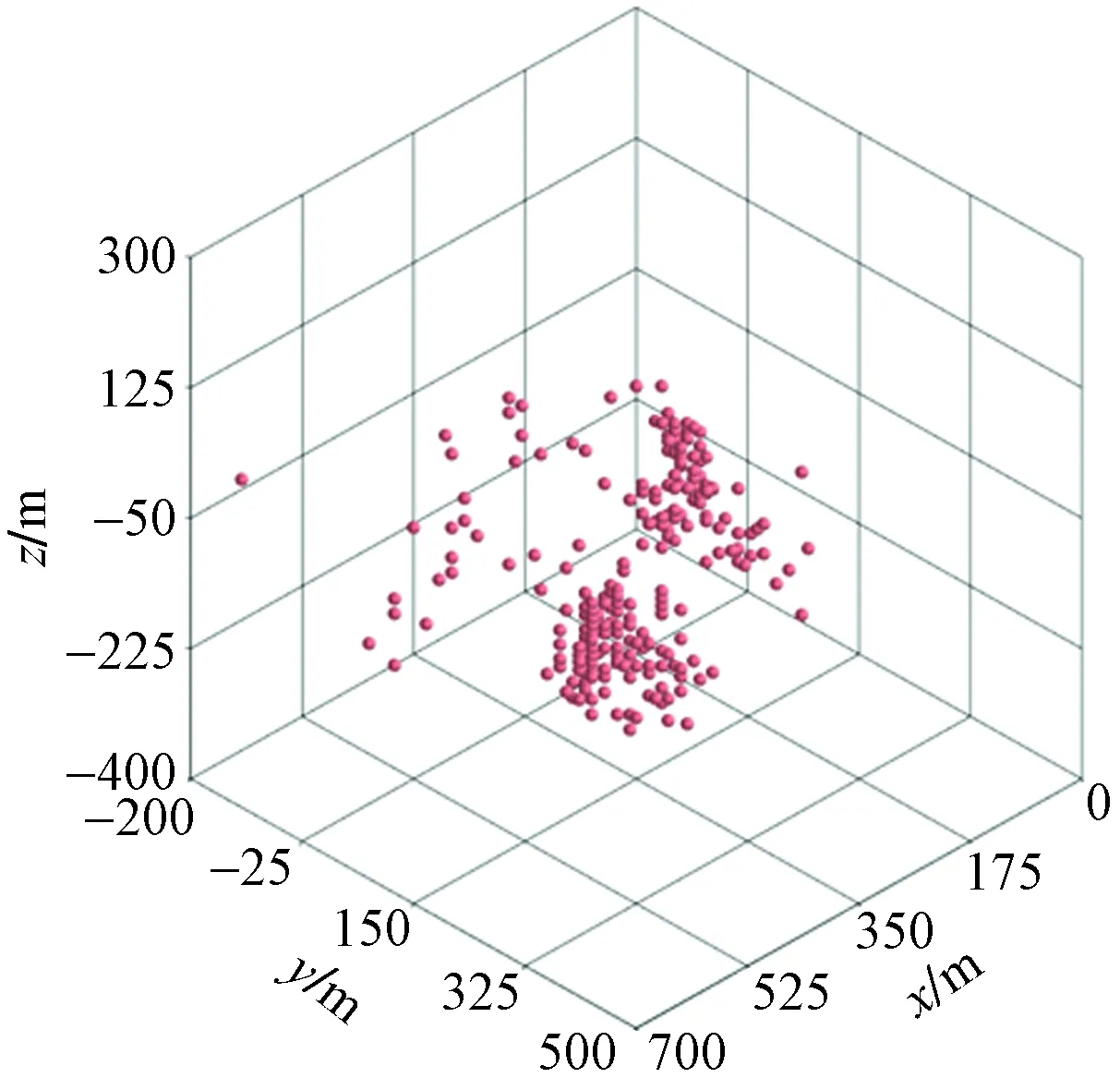
图4 单段压裂微震事件空间分布Fig.4 Microseismic event distributions in the single stage
基于微震事件的空间展布形态,结合DBSCAN算法,Eps和MinPts两个参数也被设置为50和3,对该段微震事件进行分组处理,共划分为四组。对各组微震事件分别采用MVEE算法估算出各自对应的最小体积封闭椭球体(图5)。由图5可知,各椭球体之间不存在重叠,整体压裂改造体积可表示为各椭球体体积之和1 101×104m3(表2)。本文方法也可自动计算出该段整体压裂体积为1 079×104m3,该结果与直接求和结果略有差异。产生该差异的主要原因是所选取的网格大小不同。对微震事件进行分组处理时,可结合其他信息来提高分组的合理性和准确性,例如微震事件的相对能量强弱、微震事件的发震时刻前后关系等。
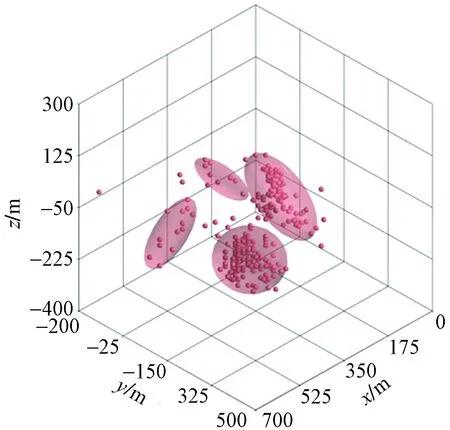
图5 单段压裂微震事件及各组有效压裂体积空间分布Fig.5 Microseismic event distributions and stimulated reservoir volume for each group in the single stage

第1组/m3第2组/m3第3组/m3第4组/m3整体m3593×10498×104363×10447×1041 079×104
3 结论
页岩储层的压裂改造体积估算对评价压裂改造效果和预测压裂后的产能具有重要的意义。结合前人成果,针对两种微震事件分布形态下的压裂改造体积估算展开研究,得到以下结论。
(1)对于单段微震事件分布形态单一的情况,使用椭球体可近似描述压裂裂缝的缝网形态,并使用MVEE算法来计算出相应椭球体的各项参数,估算出相应的压裂改造体积。考虑到实际监测数据会受到各种噪声干扰,使用DBSCAN算法消除异常点的干扰。
(2)对于单段微震事件分布形态复杂的情况,首先结合其他信息对微震事件进行划分,将复杂的分布特征拆分为多个分布特征相对简单的分组;再对各分组采用MVEE算法估算出其压裂改造体积,并消除各组对应椭球体间存在的重叠区域;最终获得该压裂段的整体压裂改造体积。
(3)选择合适处理参数有助于对压裂改造体积进行准确估计,例如聚类半径和簇内样点数的选择会影响聚类分析结果,进而影响最小体积封闭椭球的形态。因此,相关参数的选择应根据被分析数据的特征进行优化选择。
