防止3D打印模型特征偏移的自适应分层方法

2020-02-24王德鹏田晓青

合肥工业大学学报（自然科学版） 2020年1期

韩江, 王德鹏, 夏链, 田晓青

(合肥工业大学机械工程学院,安徽合肥 230009)

增材制造也称快速成型(rapid prototyping,RP)或3D打印,是用CAD设计并将材料逐层累加制造实体零件的技术[1]。先用CAD设计或反向工程获取三维模型,并转为格式简单、通用性好的STL格式;然后在选定的分层方向上,用不同高度的平面与模型相交,获得一系列的轮廓信息;再根据轮廓信息,确定打印路径及其他工艺参数,控制打印机将材料从低到高逐层堆积粘结,最后形成三维实体。3D打印加工过程以每层截面形状为底,以切片厚度为高的柱体累加形成,因此在加工倾斜表面时会产生阶梯效应,与实际模型轮廓有一定误差,分层处理作为3D打印的核心步骤会直接影响加工件表面质量及加工效率[2]。

基于STL格式的分层方法主要有等厚分层和自适应分层[3]。等厚分层层厚固定,较小层厚可获得高表面质量,但也会降低加工效率[4];自适应分层层厚不固定,而由模型几何形状和机器能力决定[5],因此自适应分层能提高工件精度。对简单模型自适应分层比等厚分层得到的层数少,加工效率更高,因此在3D打印分层中被广泛应用[5-9]。文献[5]提出了一种改进的、鲁棒的等高线结构切片算法;文献[6-7]采用一种基于自适应层厚法向图像的高效算法,以平衡复杂构造实体模型切片精度和时间;文献[8]将STL模型转换为改进边界八叉树数据结构,再计算分层厚度;文献[9]对于具有轻微曲面形状特征部位采用曲面分层,普通部位采用平面分层。这些算法主要研究层高和阶梯误差之间的关系,协调打印成型的精度和效率。除阶梯误差外,打印件还有模型特征偏移和丢失问题,而关于此问题的研究不多。在目前了解到的范围内,仅有文献[10]先用顶尖高度法对模型进行自适应分层,再找出可能存在特征的2个相邻分层面,并在这2个分层面间进行最小厚度的等厚分层。文献[11]通过计算实际打印件与原模型的体积比确定每层的分层高度,并对未被切割的三角面2个相邻分层面间进行最小厚度的等厚分层。但两者都只能保留模型特征,无法解决模型特征偏移问题。因此,本文探究了已有算法无法解决模型特征偏移的原因,并给出一种有效防止模型特征偏移问题的方法。

1 模型特征偏移分析及解决方案

1.1 模型基本特征的定义

本文讨论的模型特征是指三维模型上可表征模型形状特点且非平滑过渡的部分,即特征点、特征线和特征面[10],3种基本特征如图1所示。

图1 模型的3种基本特征

特征点在分层方向上,此点的高度为局部最高或最低,如图1中7;特征线为2个夹角大于规定阈值且均不为特征面的面交线,且此交线垂直于分层方向,如图1中1、2、5、6;特征面为垂直于分层方向的平面,如图1中3、4。

1.2 特征丢失和偏移原因分析

模型特征的丢失和偏移是指打印实体与原三维模型相比,特征未被打印出或特征所在高度发生了偏移[10],如图2所示。在图2a中,实线表示图1模型经过特征7的横截面轮廓,虚线表示分层平面;图2b中,实线为打印实体相同位置的横截面轮廓,虚线为原始模型的横截面轮廓。从图2a和图2b的对比可以看出,由于分层平面没有经过模型特征所在高度,特征6在打印实体上直接丢失,其余特征均发生了不同程度的偏移。

图2 模型特征的偏移和丢失

以往基于STL格式的分层算法中,等厚分层对模型高度均分;自适应分层对已确定的上一层分层面结合定义的特定阈值来确定下一层分层平面的高度。这2类方法都无法确保分层平面经过模型特征。文献[10-11]虽然考虑了模型特征,但仅在存在特征的地方进行等厚细分,分层平面不保证经过模型特征,导致偏移。因此打印件除特殊情况外(如模型特征比较少且高度正好与分层面高度重合),其特征会发生一定程度的偏移。由上述分析可知,保证分层平面经过模型特征所在高度,才能防止特征发生偏移或丢失。因此,针对以STL格式存储的三维模型,本文提出一种有效防止型特征偏移和丢失的自适应分层方法。

1.3 特征偏移解决方案

首先识别模型特征所在的高度,得到一组有序的高度数据作为层高;对这组层高进行调节,保证每2个相邻特征高度的间距不小于最小分层厚度;之后在每2个相邻特征高度间采用基于顶尖高度法的自适应分层方法确定层高;然后在所有层高处进行切片,得到模型切片后的所有轮廓信息;最后调整所有轮廓信息所在高度。

1.3.1 模型特征高度识别方法

(1) 特征面。平行于分层平面的三角面片即特征面,当三角面片3个顶点Z坐标相同时,判定此三角面为特征面,特征高度为顶点Z坐标。

(2) 特征线。2个相邻三角面片有且仅有两者共同的2个顶点Z坐标相同,并且这2个三角面片的二面角大于一定的阈值,特征高度为特征边上某一顶点的Z坐标。

(3) 特征点。点P为经过某一顶点的所有三角面的公共点,若点P的Z坐标高于或低于所有过该点的三角面中另外2个顶点的Z坐标,则顶点P为特征点,特征高度为顶点P的Z坐标。

1.3.2 间距调节方法

3D打印机有最大和最小可打印厚度,也称最大和最小分层厚度。若模型在某一高度区间内特征较为密集,则在对特征进行识别定位后得到的一组有序的高度数据中,就可能出现相邻2个高度的高度差d小于最小分层厚度hmin。由于打印是从低到高堆积而成的,较高的分层平面上的轮廓信息就无法打印,此时,特征偏移无法避免,需要对这2个高度进行调节。因此本文将在最大程度降低偏移量的原则下对高度进行调节。

首先,为了保证打印出的模型高度不变,且第1层和最后一层可以打印,需要对有序的特征高度序列Hlist进行预处理。方法如下:在Hlist的首部和尾部分别插入高度为0和模型最大高度的层高数据(称这2个层高为边界层高);分别检测这2个边界层高与其相邻层高的间距是否小于最小层厚,若小于,则调节相邻层高,使间距等于最小层厚;重新升序排序Hlist,检测调节后的层高与对应边界层高之间是否存在层高,若有,则删去这些层高。需要说明的是,最小层厚为打印机的最小打印厚度,调节带来的误差不会超过打印机本身的最小加工误差,因此偏差可以忽略不计。

然后,对边界层高之间的特征高度采用逐个遍历的方法进行检查,查找是否存在间距小于最小层厚的2个相邻高度,并对这2个高度进行调节。调节方法如图3所示,具体步骤如下:

图3 特征高度调节

(1) 向内合并。高度差d≤hmin/2时,将两切片层都向内偏移d/2,即合并2个层面。

(2) 向外扩张。高度差d>hmin/2时,将两切片层分别向外偏移|d-hmin|/2。

这2个被调节的高度上、下可能仍有其他相邻的特征高度,可能对相邻的2个特征高度产生影响。调节后的情况如图4所示,具体步骤如下:

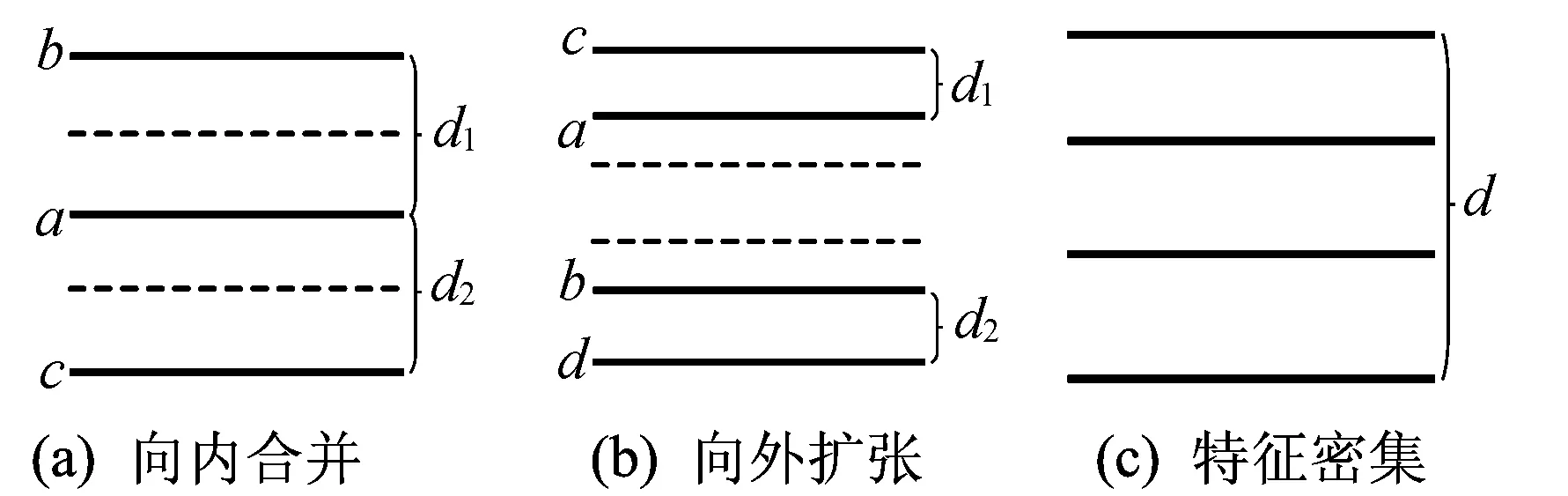
图4 特征高度调节后存在的问题

(1) 向内合并。合并后的层高a与其相邻的2个层高b、c的层高差d1、d2中至少1个仍小于最小分层厚度。

(2) 向外扩张。偏移后的2个层高与各自相邻层高c、d的层高差d1、d2中至少1个仍小于最小分层厚度。

(3) 特征高度过于密集。3个或4个连续相邻的高度中,最高的层高与最低的层高的高度差d仍小于最小分层厚度。

为方便讨论,本文以存在上述3个问题的4个相邻的层高(层高差小于最小层厚的2个层高以及这2个层高各自的另外1个相邻层高)为例说明,如图5所示,再根据问题进行相应调整。

图5 调节后存在的问题的解决方案

(1) 对于向内合并问题,若hmin≤dmax≤2hmin,则在合并中间2层层高b、c后,d1、d2均小于hmin,为了不影响其他特征高度,直接删除合并后的层高e;若dmax≥2hmin,则在合并中间2层层高b、c后,d1、d2中只有1个小于hmin,假设为d1,调节合并后的层高,使得d1=hmin。

(2) 对于向外扩张问题,若dmax<3hmin,则在向外扩张2层层高b、c后,d1、d2均小于hmin,为了不影响其他特征高度,需要调节的层高只能合并,此时,向外扩张问题转变为向内合并问题,按照向内合并问题处理方法进行处理;若dmax≥3hmin,则在向外扩张2层层高b、c后,d1、d2中只有1个小于hmin,假设为d1,调节扩张后的层高b,在保持其间距为hmin的同时,使得d1=hmin。

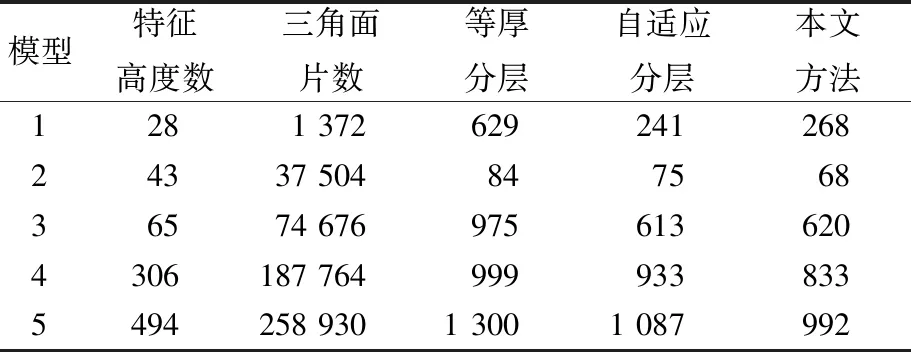
(3) 对于特征高度过于密集问题,此时dmax

1.3.3 自适应分层方法

为了兼顾加工件表面精度和加工效率,且在特征高度之间的模型不用考虑特征问题,对此部分模型直接采用顶尖高度法[12]进行自适应分层。

顶尖高度是指实际制造零件表面与CAD模型表面的最大距离,如图6所示。其中,BC为STL模型的三角面片;AB为打印件某一层的表面;AC为上一分层平面;h为当前层的分层厚度;N为三角面片的法向量;Z为分层方向矢量;θ为N方向和Z方向的夹角,范围为0～π;d为顶尖高度。对应层高计算方法如下:

(1)

cosθ=N·Z/(|N||Z|)

(2)

图6 顶尖高度

遍历与分层面BC相交的所有三角面片找到最小的h,若h低于或高于可打印范围,则将h改为最小层厚或最大层厚。再将h与分层面BC高度l相加得到当前层分层平面高度l′=h+l。循环此步骤得到对模型自适应分层的一系列层高。

在2个相邻特征高度a、b间(假设b-a=d>0)自适应分层时,需注意调节间距d。当d<2hmin时,间距过小,无法进行分层,结束对a、b间的自适应分层。当d≥2hmin时,可以对a、b间进行自适应分层,但每确定一次分层平面高度时,需计算当前分层平面距b的距离d′,若小于最小分层厚度,则调节此分层平面层高,使得d′=hmin;若调节后此分层平面距上一个相邻的分层平面的距离小于最小分层厚度,则删除此分层平面。

2 算法整体描述

本文默认分层方向与模型三角面片顶点所在的直角坐标系Z轴正方向相同。若分层方向不同于本文默认方向,则只需将模型所有三角面片顶点的三维坐标转换到以分层方向为Z轴正方向的直角坐标系中,即可使用本文提出的方法。本文算法流程如图7所示。

图7 本文分层算法流程图

2.1 读取STL文件

根据STL格式读入模型数据,三角面片的顶点存到Point类型中,包含了顶点的三维坐标；三角面片存到Face类中,包含了顶点和相邻三角面的信息。用Mesh类表示一个STL模型,包含了所有的顶点信息(vector〈Point〉points)和三角面信息(vector〈Face〉faces)。

2.2 调节顶点Z坐标

因为模型上所有顶点Z坐标中的最小值Zmin可能不为0,而本文方法的前提是Zmin=0,所以为了保证方法的正确性,需遍历模型的所有顶点,若Zmin≠0,则进行调节。调节方法如下:找到模型的Zmin,计算出偏移量Δ=0-Zmin,然后对模型所有顶点的Z坐标都加上Δ。

2.3 三角面片排序

顶尖高度法需要遍历所有与上一分层平面相交的三角平面,为了减少搜索三角面片的时间,将Mesh中的faces进行排序,按照三角面顶点中最小的Z坐标值对faces进行升序排列,当最小Z坐标相同时,则按照最大Z坐标降序排列。此时只需找到faces中第1个顶点最小Z坐标值小于等于给定高度,且最大Z坐标值大于给定高度的三角面的下标a,另外,第1个顶点最小Z坐标值大于给定高度的三角面的下标b,则faces中角标在范围[a,b)内的三角面即为要找的三角面。

2.4 确定特征高度

通过遍历一次Mesh中的faces完成对模型中所有三角面、边、顶点的判定。当遍历到某个三角面时,用1.3.1节给出的特征判定方法,对三角面、边和顶点依次进行特征面、特征线、特征点的判定,若其中一个判定为真,则不进行后续的判定;若得到的特征高度不在特征高度序列Hlist中,则将其存入Hlist中。循环此过程,直到遍历结束。最后,对序列Hlist进行升序排序。

2.5 特征高度间距调节

首先按1.3.2节的方法对有序特征高度序列Hlist进行预处理;然后开始遍历Hlist,依次找出间距小于最小分层厚度的2个相邻高度及其各自另外相邻的2个高度,计算出dmax,并判定是需要进行向内合并还是向外扩张操作;根据判定结果和dmax,判断这2个相邻的特征高度再进行向内合并或向外扩张后,是否会对各自相邻高度产生影响,若有影响,则按照1.3.2节方法进行调节。

2.6 自适应分层

在调节后的序列Hlist中依次取出2个相邻高度,并对这2个高度间的模型采用1.3.3节方法进行自适应分层。将所有自适应分层得到的高度和序列Hlist存入新的序列H并对其升序排序。

2.7 切片

按顺序从高度序列H中取出一个高度值,在Mesh中的faces里找出与此高度分层平面相交的所有三角面,计算每个三角面与此分层面的交线段,将这些线段首尾相连,即得到此层的轮廓信息。重复此过程,直到高度序列H中的高度全部被取出,则获得此模型切片后的所有轮廓信息。

2.8 调整轮廓信息高度

在实际打印时,打印出的实际层高会存在高度误差,因此需对每层轮廓的高度增加偏移量以降低误差。每层的偏移量为Δh=Δhc+ΔhZ,其中,Δhc为3D打印工艺和材料特性造成的高度偏差;ΔhZ为3D打印机Z轴精度造成的高度偏差。

3 实验与分析

使用C++语言在Visual Studio 2017开发环境下实现本文所述方法的仿真实验,因为是仿真实验,所以未进行算法的最后一步。最大和最小分层厚度根据实际机器的精度给定,顶尖高度和特征线的阈值根据用户需求给定。选取5个模型,分别用等厚分层、顶尖高度法的自适应分层和本文改进的自适应分层方法进行分层,最大和最小分层厚度分别为0.1、0.5 mm,顶尖高度设定为0.1 mm,特征线阈值取30°。为了使等厚分层产生的模型特征偏移量达到最小,等厚分层的厚度为0.1 mm。仿真分层结果见表1所列。

表1 3种分层方法的分层数结果

模型1分别用3种分层方法得到了切片仿真结果。分别将3种分层方法得到的轮廓信息存入SLC格式文件中;再分别将这3个文件与原始模型的STL文件一同导入Materialise Magics软件中,并使模型的坐标系与轮廓的坐标系完全重合;最后,测量得到模型特征的偏移量。选取模型1左下角处的特征进行比较,特征偏移量见表2所列。模型1的3种分层法切片结果如图8所示，左下角处特征偏移比较如图9所示。

表2 3种分层方法的偏移量 mm

从图8和表1可以看出,自适应分层和本文方法得到的层数相近,且均少于等厚分层层数;而特征高度数较多时,本文方法得到的层数比自适应分层少。这时由于本文方法为保证打印特征处的轮廓而使用1.3.3节中的自适应分层算法及高度调节法,可能会删除低于特征高度的相邻分层面,但只会删除1个,且删除后特征高度与较低的相邻分层面的高度差不会超过2倍的最小分层厚度,误差可以忽略不计。

图8 模型1的3种分层方法比较

从图9和表2可以看出,等厚分层和自适应分层在这5个特征处均产生一定偏移,而本文方法只在特征4处发生了细微偏移。这是由于特征4为特征线,其相邻三角面的夹角小于给定的阈值30°而没有被识别出,因而可以根据精度需求,减小阈值,提高识别率。因此,本文方法能有效防止模型偏移和丢失,保证加工精度的同时减少分层层数,提高加工效率。