全柔性空间机器人运动振动一体化输入受限重复学习控制1)

付晓东 陈力

(福州大学机械工程及自动化学院,福州 350116)

引言

空间探索进程中,为减少太空作业风险,需借助空间机器人代替宇航员完成舱外任务.空间机器人是由航天器与机械臂构成的无根多体系统,其动力学与控制的研究受到众多航天工作者重视[1-7].机械臂安装于航天器桁架导轨上,在极端恶劣的太空环境中,机械臂易受到宇宙射线,太阳风等的影响,加之执行空间任务,尤其在目标卫星的抓捕阶段,由于碰撞极易造成基座轨道安装处振动[8-9];另外,为减少发射载重以降低发射成本,构成机械臂的各杆多选用轻质细长杆,所以工作中臂杆易发生柔性变形;而且,空间机器人关节处多采用谐波减速器以驱动杆的运动,具有轻质、大承载力与大减速比等显著优点,但由于其本身的结构特性,导致关节处电机的驱动转角与被驱动杆的实际转角不同步,相当于在电机与杆之间设置了一个力矩滤波器,引入了关节柔性[10-12].因此,空间机器人系统是一个刚性运动与基座、臂、关节柔性振动高度耦合的刚柔复合系统,其各部件柔性严重影响机器人工作精度与性能.为减少柔性对机器人控制精度的影响,往往采用“低速,缓动”操作模式,这种模式下,柔性振动影响不突出,整个系统可看作刚性系统.迄今为止,刚性模型假设下的空间机器人动力学响应分析及运动控制相对成熟[13-17].然而,由于太空环境的特殊性,对空间机器人可靠性要求非常高.面对未知的太空环境与复杂的空间任务,系统柔性很容易被激振,一旦基座、臂、关节某部件柔性振动被激发,可能导致系统所有柔性部件的振动,在无阻尼的太空环境中衰减缓慢,如果不对其进行有效抑制,会使执行器发生剧烈振动甚至失效,严重影响机器人工作可靠性.因此,考虑空间机器人基座、臂、关节的柔性效应并主动抑制其振动值得人们关注.

近些年,柔性空间机器人的研究取得一定进展.针对臂杆柔性,Kumar 等[18]讨论了单柔性杆空间机器人的动力学模拟与控制问题;Wang 等[19]用假设模态法处理单柔性杆,讨论了其动力学建模,刚性控制与柔性振动抑振问题;于潇雁等[20]考虑两杆均存在柔性的情况下空间机器人动力学响应分析与振动主动抑制问题.针对关节柔性,Nanos 等[21]讨论了双柔性关节空间机器人的动力学模拟与控制问题;Chu等[22]针对高精度柔性关节伺服系统的位置控制问题,提出了反推控制方案.针对存在两类柔性部件系统,谢立敏等[23]讨论了单柔性杆、双柔性关节空间机器人的动力学建模与控制问题;陈志勇等[24]讨论了弹性基座、双柔性关节空间机器人的动力学模拟与双重振动抑振问题.

值得一提的是,上述研究仅考虑空间机器人基座、臂、关节某一类或两类部件柔性的影响,属于部分柔性空间机器人系统.基座、臂、关节全柔性空间机器人系统是刚性运动与三重柔性振动高度耦合、高度非线性的时变系统,其动力学模拟非常繁杂,控制器设计面临着实现刚性轨迹跟踪,抑制基座、臂、关节柔性振动四重功能共存的突出难点[25].这使得全柔性空间机器人动力学模拟与控制问题较难分析,相关研究鲜有报道.针对这些问题,本文提出了柔性基座、两柔性杆、两柔性关节空间机器人的动力学建模方法,以及系统刚性运动与三重柔性振动的解耦方案.

另外,考虑到太空任务复杂,搭建空间站,维护航天设备,回收失效卫星,清理轨道垃圾等任务中周期重复工作都占有很大比重[26-28].而传统的控制器,执行周期性任务,可以实现渐进跟踪,但对于周期重复出现的误差,系统响应无法改善,导致控制精度不高.重复项的引入,能补偿周期性误差,提高控制精度[29].最近,地面机器人重复学习控制研究相对成熟,Califano 等[30]提出指数稳定的重复学习算法,Verrelli 等[31]论证最小相位非线性系统的重复控制方法,Sun 等[32]提出了跟踪误差收敛于有限时间内的重复学习算法,Verrelli 等[33]提出不确定周期的重复控制算法.然而,作为高精度运动的有效控制策略,其在全柔性空间机器人系统中的应用比较少见.而且,载人航天成本高昂,机器人控制液宝贵,由于驱动能量的有限与机械构造的限制,其关节输入力矩是有饱和值的,限制力矩输入就变得很有必要.所以,在运动控制方面,设计了输入受限重复学习控制算法,满足力矩受限要求的同时,实现对周期信号的高精度追踪.

基于上述两方面的分析,本文提出基座、臂、关节全柔性空间机器人运动振动一体化输入受限重复学习控制器.利用假设模态法与拉格朗日方程建立模型,采用奇异摄动法分解模型,将基座与关节的柔性等效在快变时标下分析,刚性运动与臂的柔性等效在慢变时标下讨论.而为了抑制慢变子系统中臂的柔性振动,运用虚拟力的概念,设计能实现刚性轨迹跟踪与臂柔性抑振的基于虚拟力的输入受限重复学习控制器.对于快变子系统,利用线性二次最优控制方案同时抑制基座与关节双重柔性振动.最后仿真分析,校验了算法的可行性.

1 全柔性空间机器人系统动力学模型

1.1 系统动力学简化模型

漂浮柔性基、柔性臂、柔性关节空间机器人结构模型如图1 所示,由漂浮载体B0,近载体端的柔性杆B1,远载体端柔性杆B2组成.OC0为载体B0的质心,OC为系统的总质心,Oi为连接Bi−1与Bi关节铰的几何中心(i=1,2).建立惯性坐标系OXY与各分体的连体坐标系Oixiyi,令xi轴的轴向单位向量为ei(i=0,1,2),柔性杆Bi主轴坐标系xi轴的径向单位向量为O0与OC0重合.假设系统在OXYZ平面内做平面运动.r0与rC分别表示载体质心与系统总质心在惯性坐标系下的位置矢量,ri表示柔性杆Bi上任意一点相对于O的矢径(i=1,2).qb为载体与杆B1铰接处载体柔性变形量,q0为惯性坐标系下基座相对于Y轴的转角,qi为杆Bi的相对转角,qmi为关节电机转子转角(i=1,2).xi为柔性杆Bi主轴坐标系xi上任意轴向距离,vi(xi,t)为t时刻柔性杆Bi在xi处径向柔性位移(i=1,2).基座无弹性变形时,OC0与O1的距离为l0,载体质量为m0,转动惯量为J0.杆Bi初始长度为li,密度为ρi(i=1,2).电机转子质量忽略不计,转动惯量为Jmi.

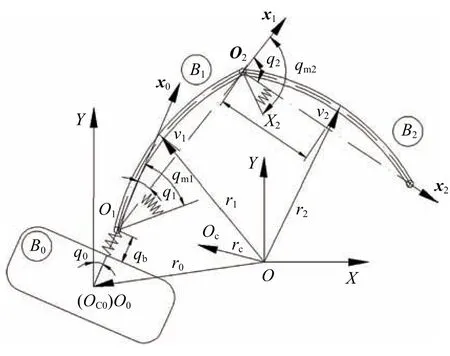
图1 基座、臂、关节全柔性空间机器人系统Fig.1 Space robot system with flexible base,flexible links and flexible joints

本文将柔性基座与柔性关节分别等效为无质量的线性伸缩弹簧和线性扭转弹簧,假设基座与关节的柔性系数均为定值,分别用kb和kmi表示.将两杆均等效为简支梁,取其抗弯刚度EIi为定值,杆径向变形表达式为其中ϕij,δij分别表示杆Bi的第j阶模态函数与模态坐标,ϕij(xi)=sin[(jπ/li)xi],i,j=1,2,n为保留模态数,本文取n=2.经计算,杆Bi的等效刚度系数为

1.2 系统动力学建模

根据系统在惯性坐标系中的位置关系得

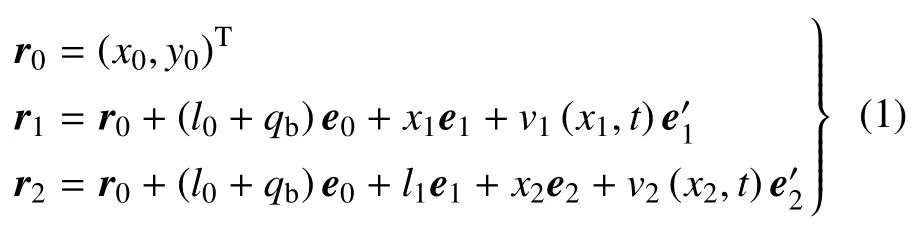
其中,x0,y0为载体质心坐标.

系统总质量为

根据质心定理,得

由式(1)∼式(3)得,各分体矢径表达式

式中,Γ00∼Γ26为惯性参数组合函数.

本文全柔性空间机器人系统的动能主要考虑基座、两杆及两电机转子的动能,设系统初始动量为0,即对式(4)求导,得系统各分体动能为

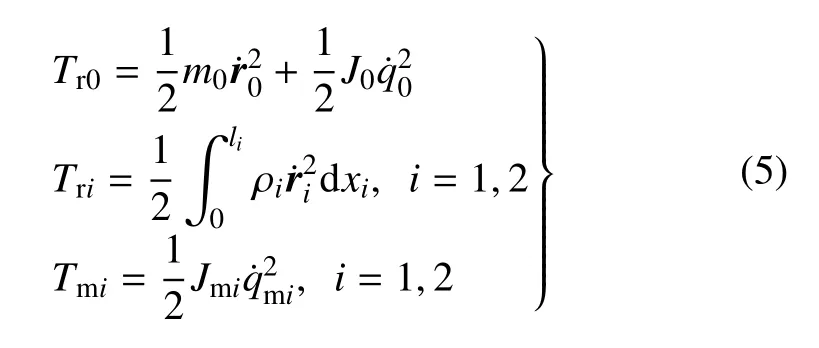
其中,Tr0表示基座的动能,Tri表示杆Bi的动能,Tmi表示关节铰Oi处电机转子的动能(i=1,2).

系统总动能为

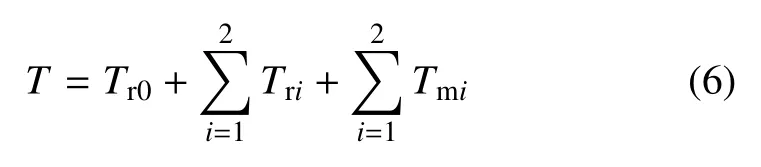
忽略重力,全柔性空间机器人系统的势能主要由基座、杆及关节的振动引起,各部分势能如下

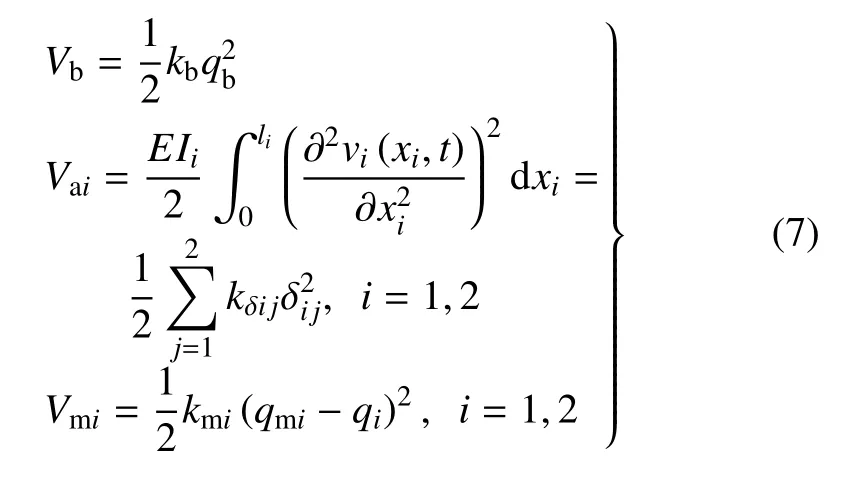
其中,Vb表示柔性基座的势能,Vai表示杆Bi的势能,Vmi表示Oi处柔性关节的势能(i=1,2).

系统总势能为

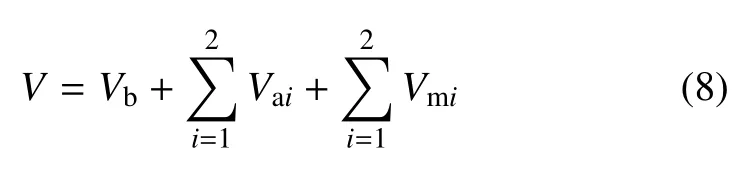
令L=T-V为拉格朗日函数,将式(6)、式(8)代入拉格朗日方程,得载体姿态受控全柔性空间机器人动力学模型为

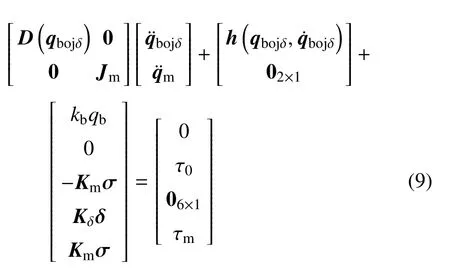
为便于后文分析,式(9)重新写为

2 全柔性空间机器人模型分解及其特性

基座、臂、关节全柔性空间机器人运动振动主动控制问题中,突出难点在于存在三重柔性,主动抑制其中一类柔性会造成另一类的激振,控制难度大.为解决上述问题,利用奇异摄动法,将系统柔性等效在不同时标下考虑.

2.1 模型奇异摄动分解

设计带关节柔性补偿的总控制器为

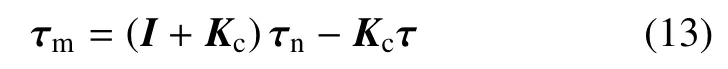
式中,I∈R2×2为单位矩阵,Kc∈R2×2为对称正定柔性补偿矩阵,τn∈R2×1为待设计的控制器,表达式为

式中,τns∈R2×1为慢变子系统控制器,τnf∈R2×1为快变子系统控制器.

将式(13)代入式(11),有

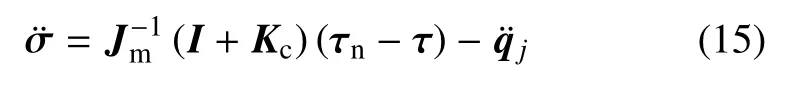
为方便后文计算,式(10)重新写为

式中,Dbb,Hbb∈R1×1,Dba,Hba∈R1×7,Dab,Hab∈R7×1,Daa,Haa∈R7×7.

定义

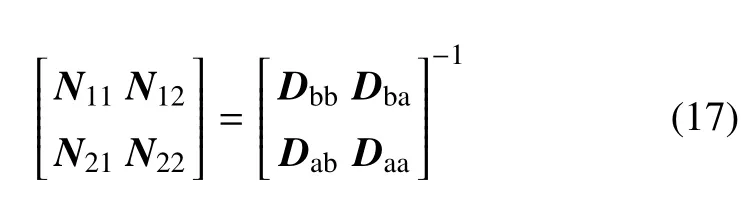
令qojδ为慢变子变量,qb和σ 为快变子变量,µ=1/min(kb,km1,km2)为奇异摄动因子.kbf=µkb,Kmf=µKm,qbf=qb/µ,σf=σ/µ.将式(17)代入式(16)进行慢、快变子系统刚柔性解耦,再将kbf,qbf,Kmf,σf表达式与µ=0,τnf=0 分别代入式(15)与解耦结果式得

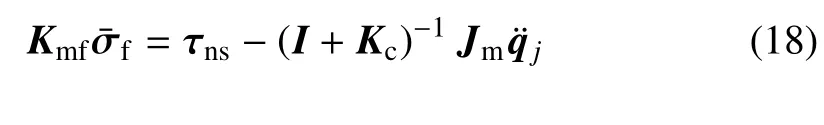
已知存在如下关系式

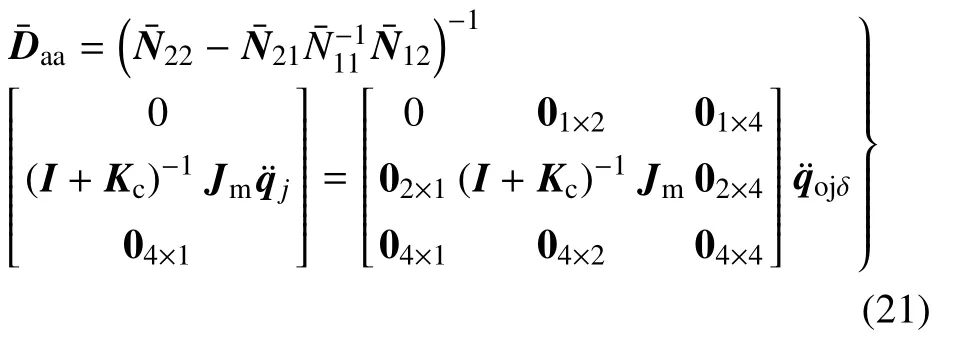
将式(18)、式(19)代入式(20),再将式(21)代入结果式,得慢变子系统动力学方程

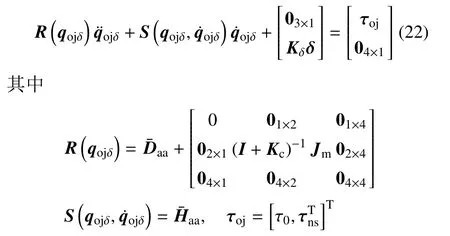
为便于基于虚拟力概念的控制器设计,式(22)重新写为

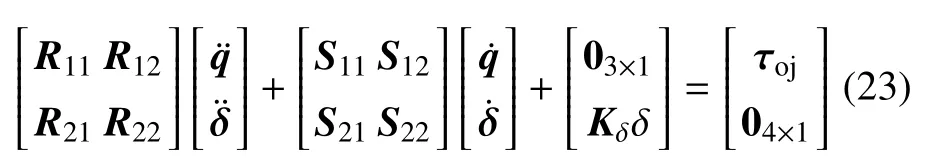
其中,R11,S11∈R3×3,R12,S12∈R3×4,R21,S21∈R4×3,R22,S22∈R4×4.

式(23)刚柔性分解得

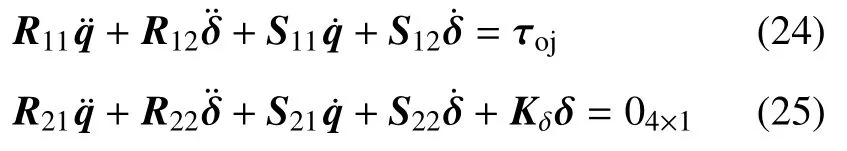
将式(25)代入式(24)得刚性系统动力学模型

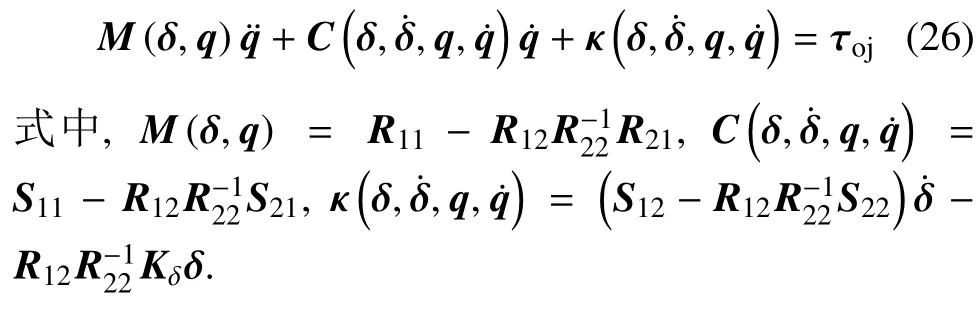
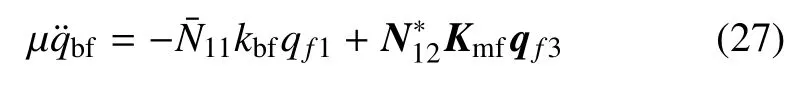
将qf3与式(14)、式(18)代入式(15)得

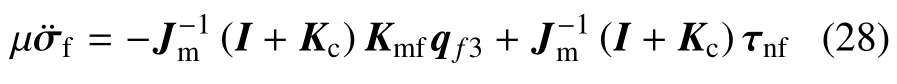
qf在快变时标下求微分,并代入式(27)、式(28)得快变子系统动力学方程

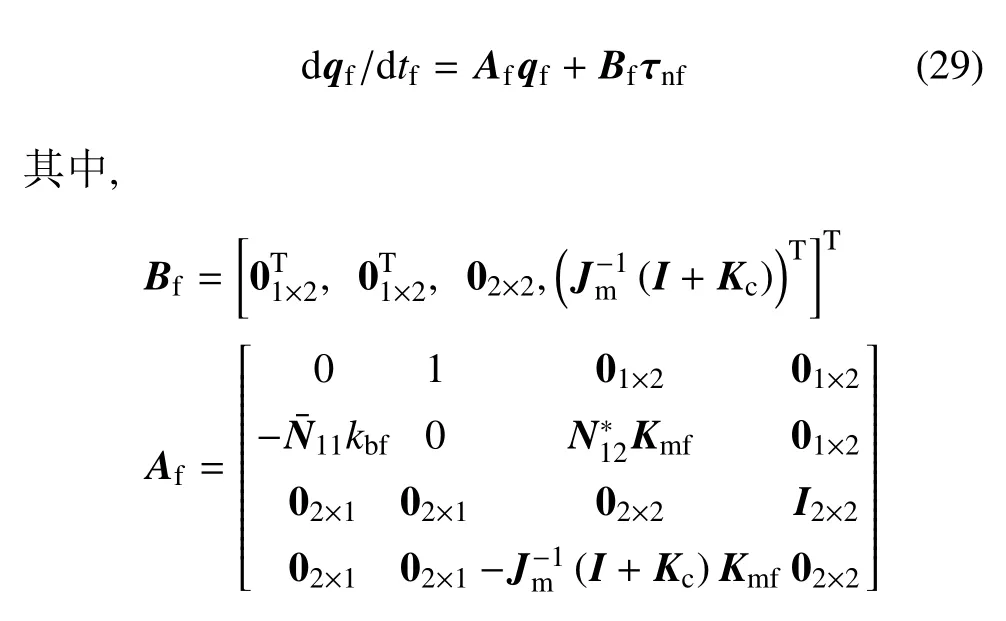
2.2 动力学模型特性

注意到式(26)是全驱动的动力学模型,形式与刚性机械臂相似,具有如下结构特性[34-35]:

特性1惯性矩阵M(x)对称正定有界,即

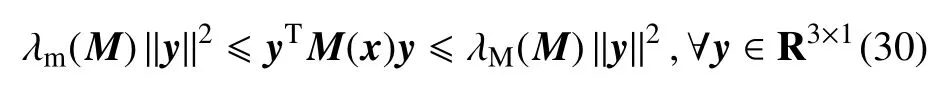
其中,λm(·)和λM(·)分别表示矩阵的最小和最大特征值,‖·‖表示二范数.

特性2科氏力、离心力矩阵C(x,y)∈R3×3满足

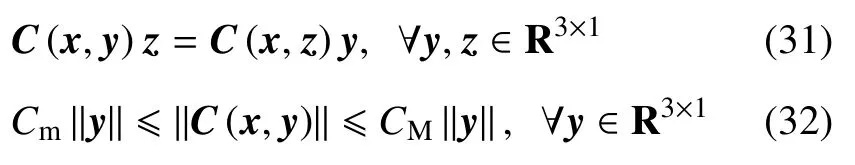
式中,Cm,CM是已知正常数.

特性3为交错矩阵,满足

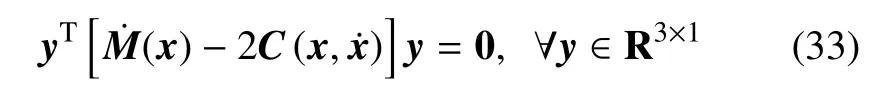
特性4存在正常数kM,kC1,kC2对于任意矢量x,y,z,x1,y1,x2,y2∈R3×1满足关系式

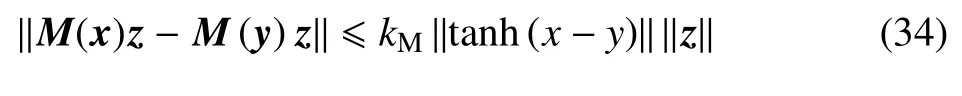
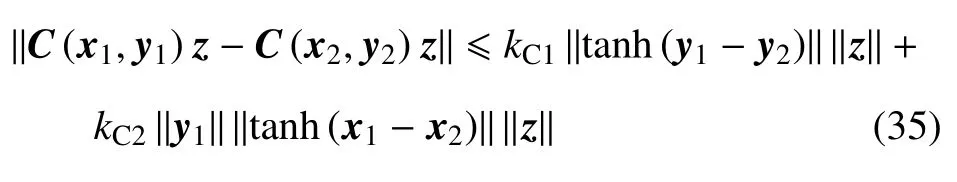
其中,kM,kC1,kC2的取值参考文献[34],tanh(·)如式(43)所定义.

特性5 κ(x,y)满足关系式

其中,kC3,kC4的取值参考Kelly 等[34].

3 控制器设计

3.1 慢变子系统输入受限重复学习控制器设计

连续可微周期期望轨迹qd(t)满足条件

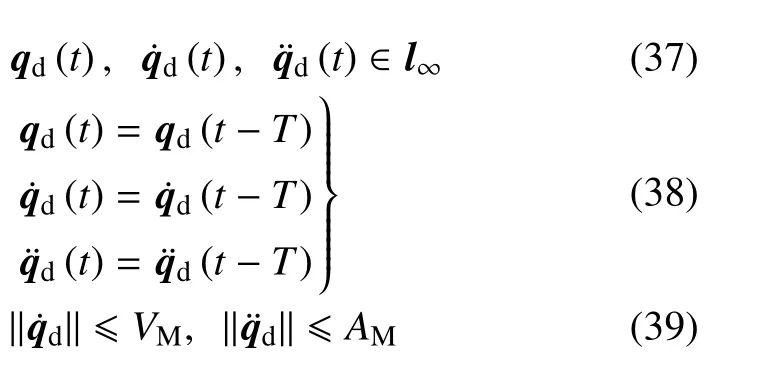
其中,T为已知周期,VM,AM为期望速度与加速度范数的上界.

结合式(26),机器人期望输入力矩τd为

其中,τd(t)是以T为周期的周期函数,用傅里叶级数展开为

式中,ω=2π/T为角频率为未知常矢量.

结合式(30)、式(32)、式(36)、式(37)、式(39)与式(40)得,τd(t)是有界函数,满足

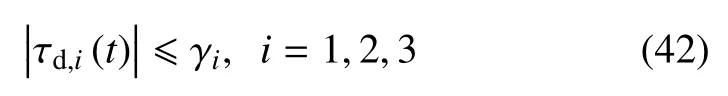
其中,τd,i(t)表示τd(t)的第i个元素,γ=是已知的正常数矢量.

定义矢量sgn(·)∈R3×1,tanh(·)∈R3×1,sat(·)∈R3×1 为

其中η∈R3×1,令输出误差e,为

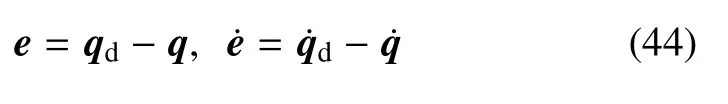
引入滑模变量s∈R3×1为

设计有限维输入受限重复学习控制器为

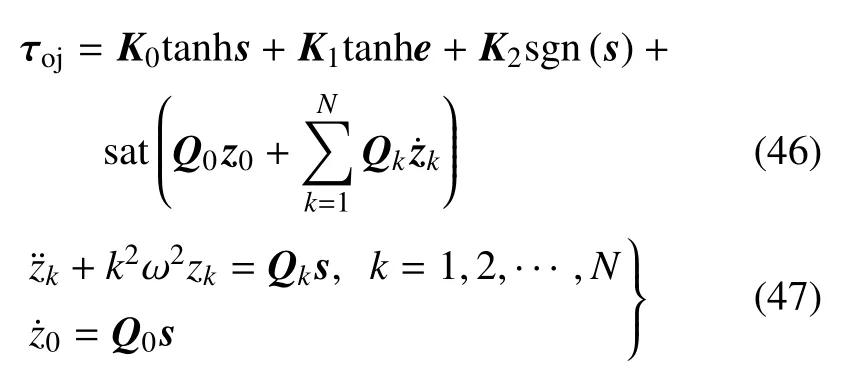
其中,K0,K1,K2,Q0和Qk(k=1,2,···,N)是3×3的常正定对角矩阵,N为谐振子数量.为重复学习控制器(repetitive learning controller,RC),sat(·)为重复项饱和函数,其元素为

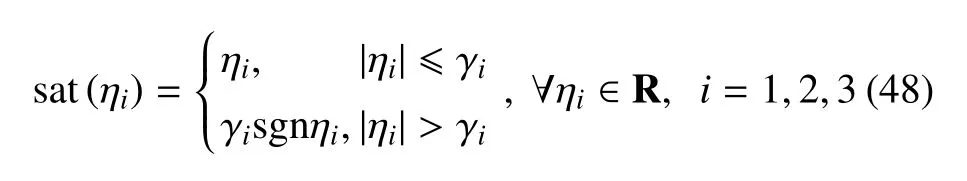
考虑双曲正切函数,符号函数,饱和函数的性质,由式(46)得输入力矩满足关系式

其中,τoj,i表示τoj的第i个元素,k0,i,k1,i,k2,i分别为K0,K1,K2对角线上第i个元素.假设τoj,i,max为空间机器人基座或关节最大控制力矩,合理选择控制器参数,可使系统满足输入受限条件,即k0,i+k1,i+k2,i+γiτoj,i,max.

现求闭环系统方程,式(45)对时间求导,结果式两边同乘M(δ,q),并代入式(26)得

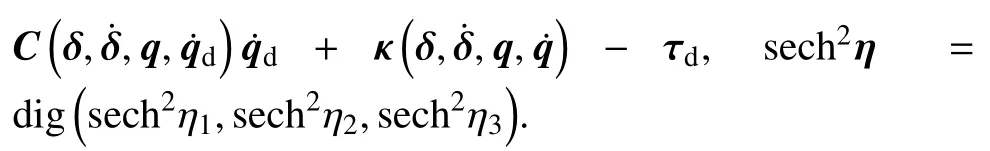
将式(31)、式(44)、式(45)代入X表达式得

对式(51)求范数,并利用特性1 与2 得

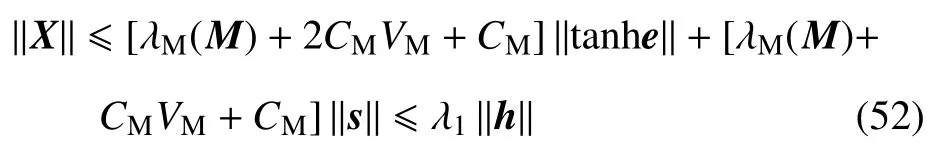
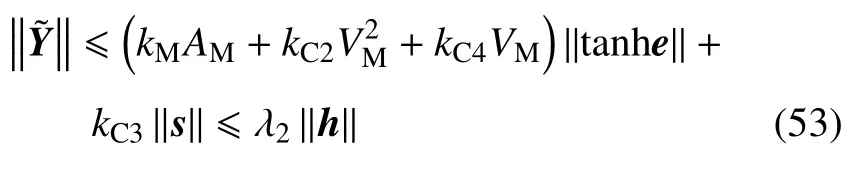
其中,h=[tanhTe,sT]T.

定理1对于刚性子系统式(26),在满足如式k0,i+k1,i+k2,i+γiτoj,i,max所示的输入受限条件下,若控制器增益满足如下条件

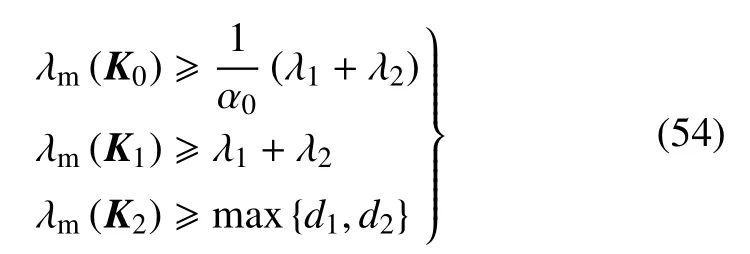
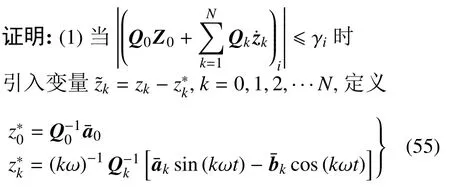
将式(41)、式(46)、式(55)代入式(50),得闭环系统误差方程,为

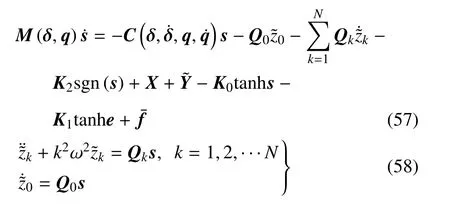
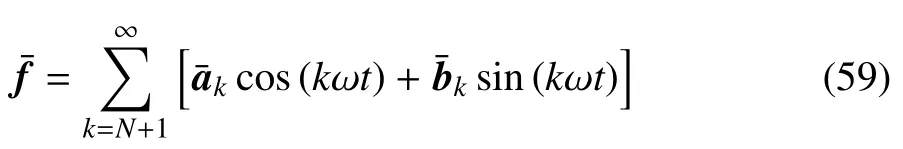
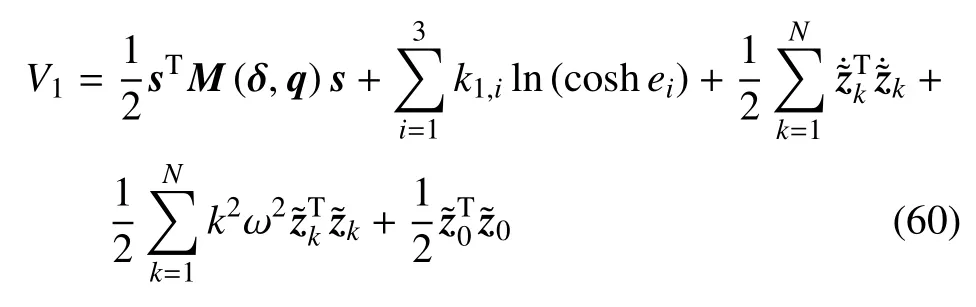
合理选择α0,使满足以下关系式

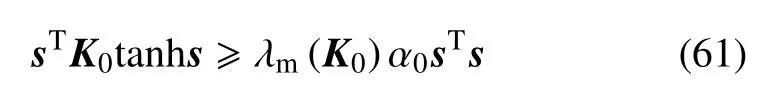
式(60)沿闭环轨迹式(57)∼式(59)求微分,并代入特性3 与式(45)得

将式(52)、式(53)、式(61)代入式(62),并在结果式中代入式得

将式(46)代入式(50)得闭环系统误差方程为

其中,Γ=diag(γ1,γ2,γ3).

构造李雅普诺夫函数V2为

式(65)沿闭环轨迹式(64)求微分得

由于τd∈l∞,结合范数性质得

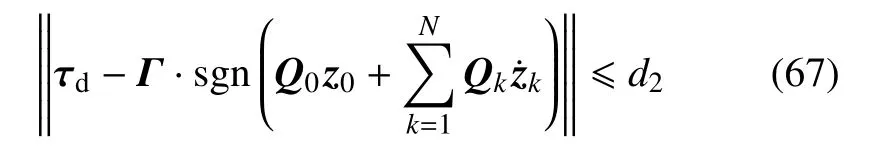
将式(52)、式(53)、式(61)、式(67)代入式(66)得

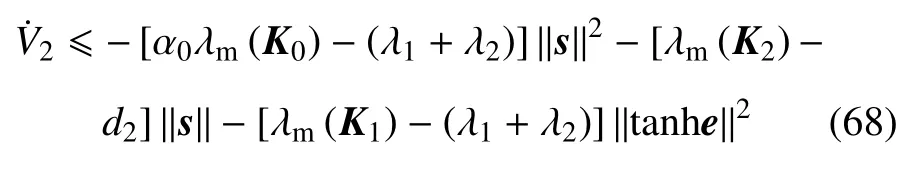
3.2 慢变子系统控制器设计

由于上节设计的输入受限重复学习控制器仅能保证慢变系统中刚性运动对期望轨迹的渐进跟踪,而不能对两杆柔性振动主动抑制,因此,本节使用虚拟控制力原理,对原有的期望轨迹进行修正,生成同时反映臂柔性振动和刚性期望轨迹的混合轨迹qh.然后设计基于虚拟力概念的输入受限重复学习控制器,实现运动跟踪与两杆振动主动抑制双重功能.引入虚拟力F∈R3×1,期望轨迹与混合轨迹误差为eh=qd−qh,由如下二阶指令发生器生成

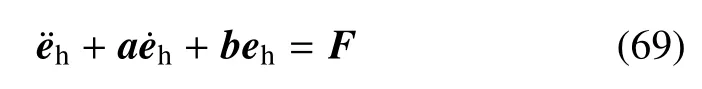
其中,a,b∈R3×3为正定常值对角矩阵.

定义混合误差er=qh−q,混合滑模变量为sr=+tanher,将控制器式(46),式(47)中qd,e分别替换为qh与er,得基于虚拟力的输入受限重复学习控制器为

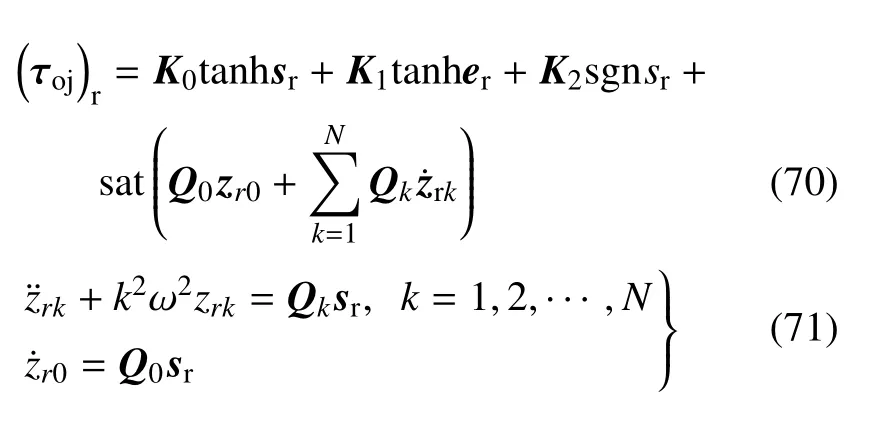
将控制器式(70),式(71)代入刚性系统式(26)得

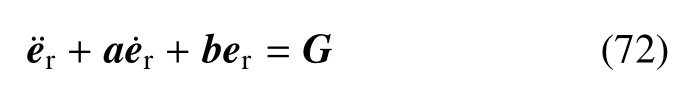
式(69)与式(72)相加得

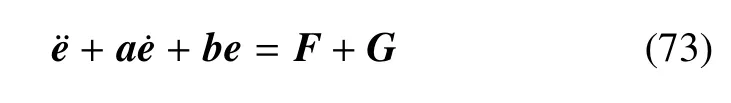
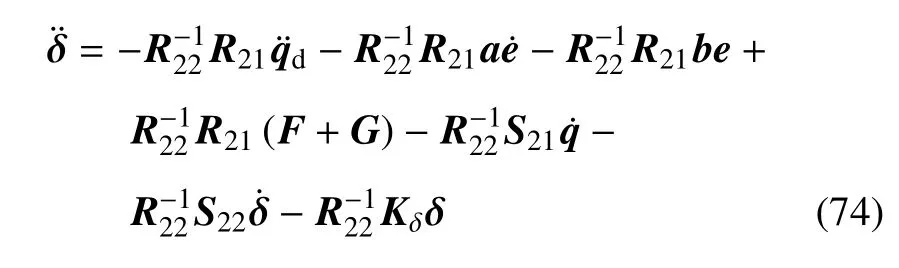
定理2对于状态方程当Ls=014×1或满足以下条件式(76),取F=则系统稳定.

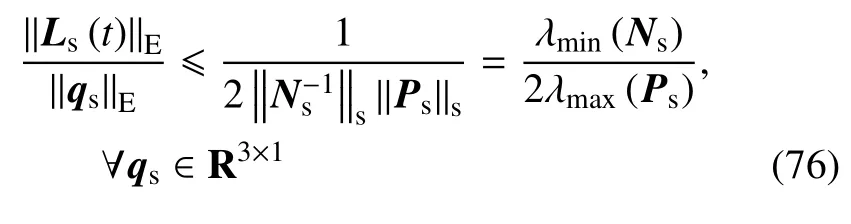
证明:当Ls=014×1时,对于系统构造性能指标函数为

其中,对称权阵Qs0,Rs>0,于任意矩阵ℜs,有若如下黎卡提方程式(78)的解Ps对称正定,则阵对完全可观.

又因为阵对{As,Bs}完全可控,所以系统存在最优控制

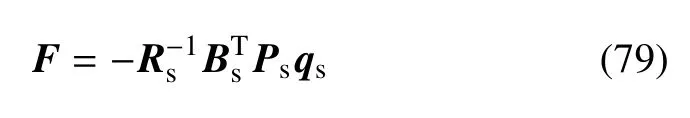
当Ls014×1时,将式(79)代入式(75)得

构造李雅普诺夫函数V(qs)=V(qs)对时间求导,并代入式(80)及Ns得

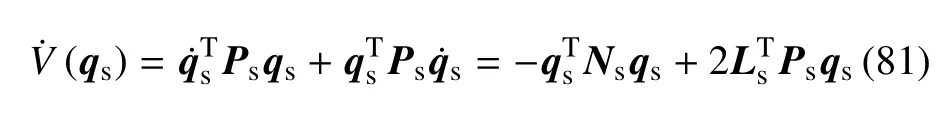
根据条件式(76)得

将式(82)代入式(81)得

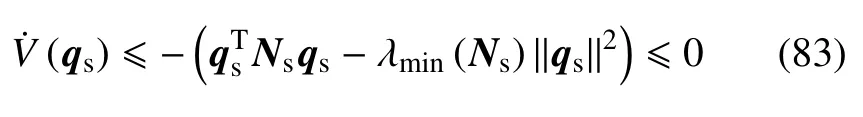
所以系统是稳定的,证毕.

3.3 快变子系统控制器设计

同上文分析,快变子系统中,qf在快变时标tf下的状态方程如式(29).构造性能指标函数

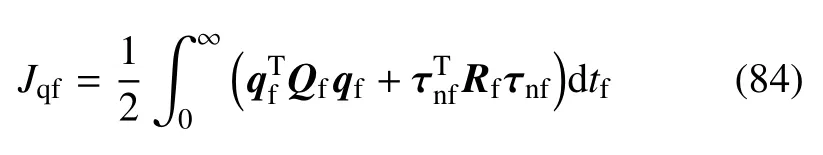
其中,对称权阵Qf0,Rf>0.

则快变子系统最优控制为

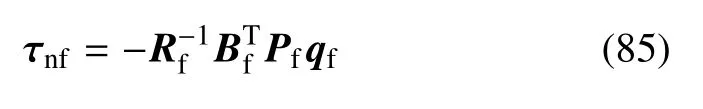
其中Pf为如下黎卡提方程的解

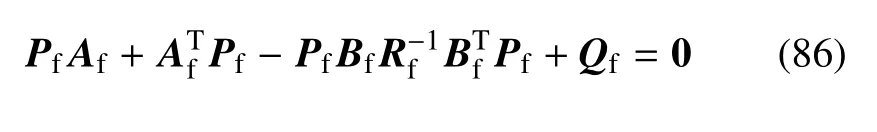
4 仿真算例分析

为了验证式(13)、式(14)、式(70)、式(71)、式(85)构成的运动振动一体化输入受限重复学习控制器(an input limited repetitive learning controller with integration of motion and vibration,ILRCI)的有效性,对图1 所示的系统进行仿真分析.全柔性空间机器人参数选取为:m0=40 kg,l0=l1=l2=1.5 m,J0=30 kg·m2,ρ1=3.5 kg·m,ρ2=1.1 kg·m,Jm1=Jm2=0.1 kg·m2,EI1=EI2=100 N/m2,km1=km2=50 N·m/rad,kb=500 N/m.取控制参数:K0=dig(200,40,20),K1=dig(10,5,1),K2=dig(10,10,2),KC=dig(104,88),Q0=dig(15,40,25),Qk=dig(20,20,20),k=1,2,···,N,N=3,a=b=dig(5,5,5).

广义坐标初值为qbojδ(0)=[0 m,1.9 rad,0.7 rad,0.5 rad,0 m,0 m,0 m,0 m]T,qm(0)=[0.7 rad,0.5 rad]T,

图2 ILRCI 控制下基座姿态与关节角的轨迹追踪曲线Fig.2 Trajectory tracking curve of base attitude and joint angle under ILRCI

周期性期望轨迹为qd=[1 rad,0.8 rad,1.2 rad]T,仿真步长取0.01 s.图2 给出了全柔性空间机器人基座姿态、关节在ILRCI 控制下的轨迹追踪曲线.图3 为开启或关闭ILRCI 控制中RC 时,基座姿态、关节的跟踪误差收敛曲线.图4 为开启或关闭ILRCI控制中τnf时基座与关节的柔性抑振曲线.为了对比验证虚拟力对杆的抑振效果,采用式(13)、式(14)、式(46)、式(47)、式(85)构成的关闭虚拟力的ILRCI控制重新仿真.图5 为ILRCI 控制中虚拟力对柔性杆Bi的抑振效果图.

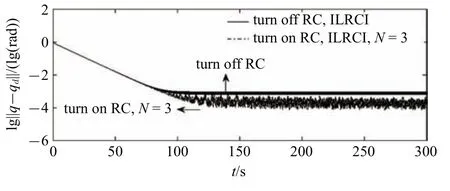
图3 ILRCI 控制与关闭RC 后ILRCI 控制的误差收敛曲线(单位:rad 以10 为底取对数)Fig.3 Error convergence curve of ILRCI and ILRCI without RC

图3 表明,RC 可以提高系统的轨迹跟踪精度.图4 表明,快变子系统控制器τnf能实现对系统基座、关节柔性振动的有效抑制.图2、图5 表明,所提的ILRCI 能确保轨迹精确追踪的同时,实现对柔性杆振动的有效抑制.本文机器人关节柔性大,所以采用关节柔性补偿间接增大其等效刚度.关闭柔性补偿,重新对系统进行仿真运算,图6 为前1 s 的仿真结果,系统发散,可见奇异摄动法仅适用于弱柔性非线性系统.而本文设计的关节柔性补偿器,可实现对一般柔性非线性系统的奇异摄动分解与有效控制.

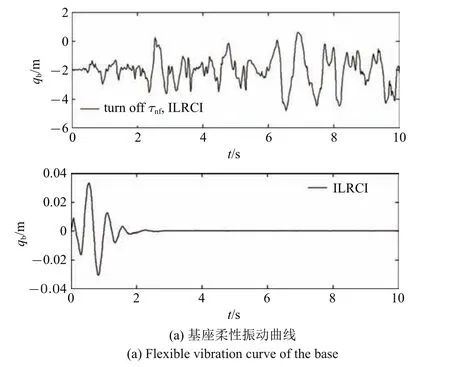
图4 ILRCI 控制与关闭τnf后ILRCI 控制的仿真结果Fig.4 Simulation results of ILRCI and ILRCI without τnf

图5 ILRCI 控制与关闭虚拟力F 后ILRCI 控制的仿真结果Fig.5 Simulation results of ILRCI and ILRCI without virtual force F

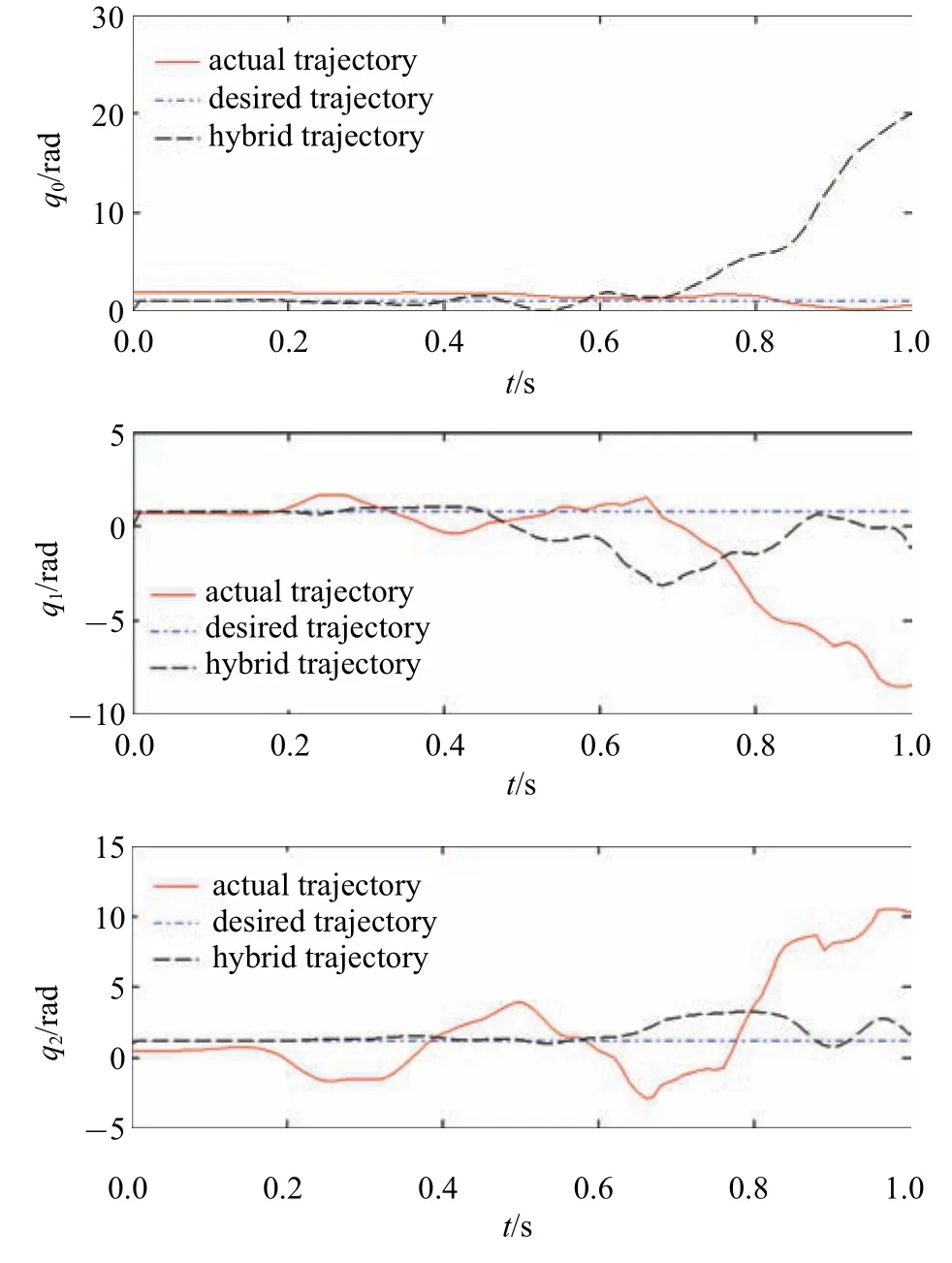
图6 关闭关节柔性补偿后ILRCI 控制的仿真结果Fig.6 Simulation results of ILRCI after closing joint flexible compensation controller

更进一步,为了验证所提算法的力矩受限情况,分析ILRCI 控制所需的驱动力矩,仿真结果如图7 所示.可以看出,实时力矩的最大上界[150,40,23]T,根据式k0,i+k1,i+k2,i+γiτoj,i,max得,仿真运算中式中,是矢量对应的元素,i=1,2,3,所以力矩受限.

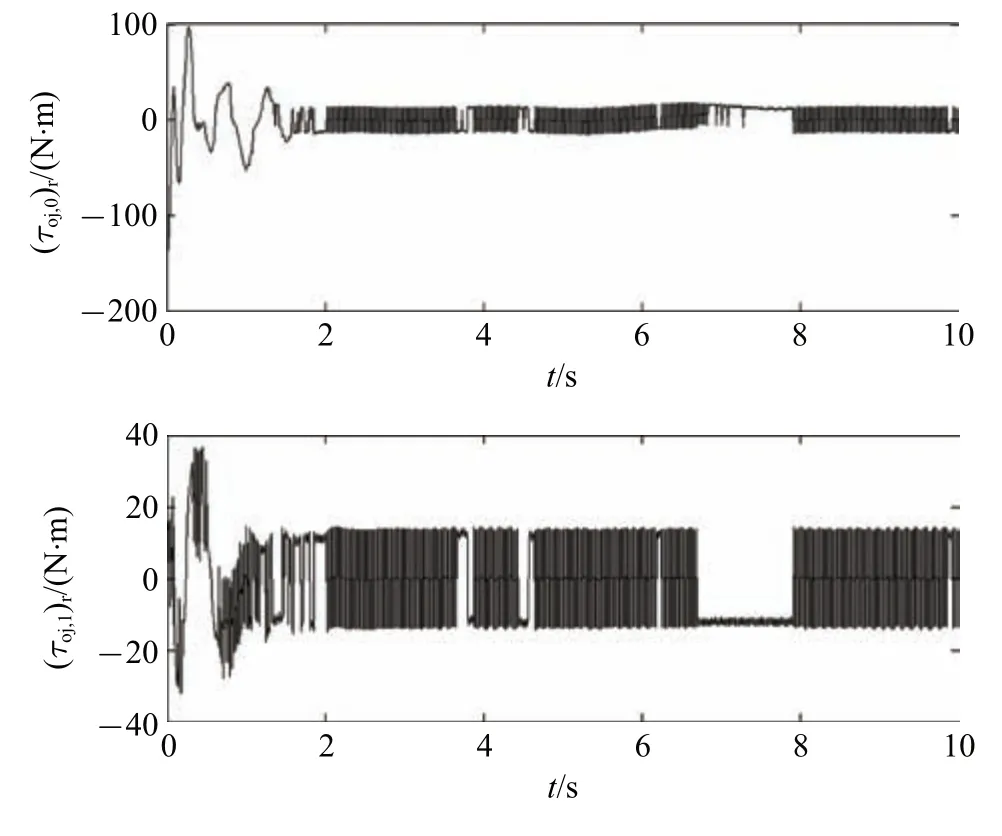
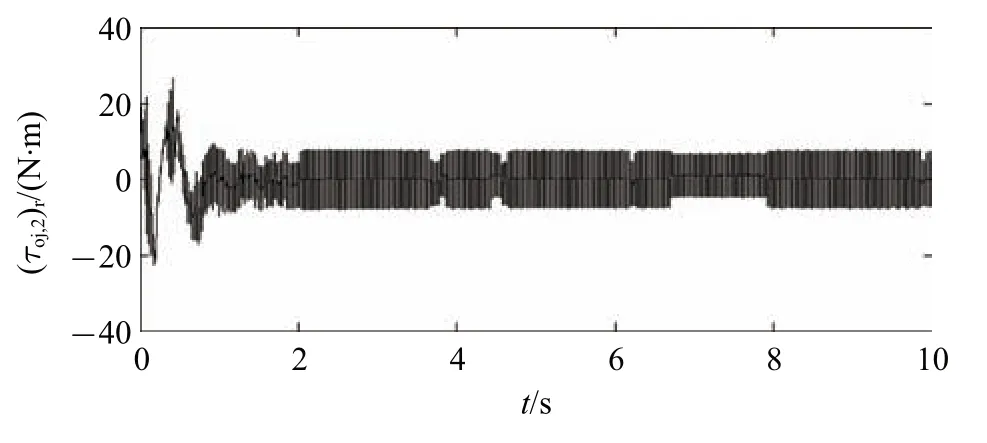
图7 ILRCI 控制的驱动力矩Fig.7 Torques of ILRCI

5 结论

利用假设模态法与拉格朗日第二类方程,建立基座、臂、关节同时存在柔性的空间机器人动力学模型.根据奇异摄动法,将模型解耦为双时标下的慢变子系统与快变子系统.对子系统分别设计控制器.提出基于虚拟力概念的慢变子控制器,具有如下优点:第一,控制器不基于模型信息设计;第二,适用于驱动力矩饱和情况;第三,能补偿周期重复出现的误差,精确追踪周期信号;第四,可以有效抑制臂杆的柔性振动.基于线性最优控制设计的快变子控制器,可同时抑制基座与关节的柔性振动.上述两种算法组成的一体化控制器中引入关节柔性补偿,使系统动力学模拟与控制适用于一般柔性非线性系统.仿真算例,验证了算法的有效性.