基于联系观的高考试题共性研究视角

湖北省恩施州教育科学研究院(445000) 周 威

2018年3月，教育部考试中心主任姜刚在《牢记立德树人使命写好教育考试奋进之笔》一文中说道，高考应积极“引导教学”，树好“一面旗”，大力助推素质教育.这就意味着对高考试题的研究不仅仅是备考，更是我们平时教学中的导向！若能基于联系的观点对同类型高考题进行共性研究，更能总结解题思路、方法，便于在关联的情境中进行解题教学，在新情境中帮助学生学会选择和运用数学方法解决问题.

一道试题通常包括显性要素和隐性内涵，而显性要素就是我们能看到情境与设问形式，隐性内涵包括试题立意、问题本质、核心素养的体现等.联系观是唯物辩证法的总特征之一，其强调事物与事物之间、事物内部诸要素之间是普遍联系的，本文以2019年高考数学解析几何题为研究对象，基于联系的观点从试题的显性与隐性方面阐述共性研究的几个视角.

一、试题立意中的共性研究

问题形式中的共性，往往能体现出试题立意.试题立意一般包括知识立意、能力立意、素养导向.知识立意包括基础知识、基本方法等，是“四基”的一种体现.通过联系的观点，对不同省份高考试题的立意进行共性研究可以发现，它往往具有共同的问题形式或基于某一共同的性质或定理.

例1(2019年高考北京卷文科第19 题)已知椭圆的右焦点F，且经过A(0,1).

(1)求椭圆C的方程;

(2)设O为原点，直线l:y=kx+t(t±1))与椭圆C交于两个不同的点P,Q，直线AP与x轴交于点M,直线AQ与x轴交于点N，若|OM||ON|=2，求证直线l经过定点.

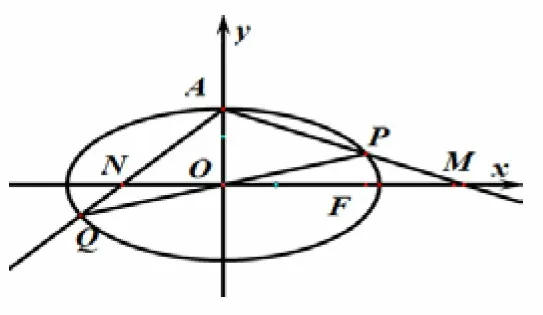
图1

解析(1)

(2)如图1，设P(x1,y1),Q(x2,y2)，将l:y=kx+t代入椭圆方程得，(2k2+1)x2+4ktx+2t2-2=0，则

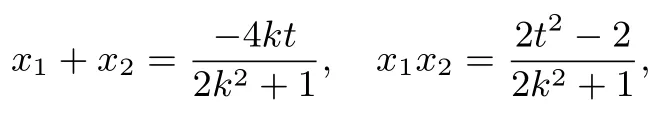
直线AP的方程为所以同理可得故

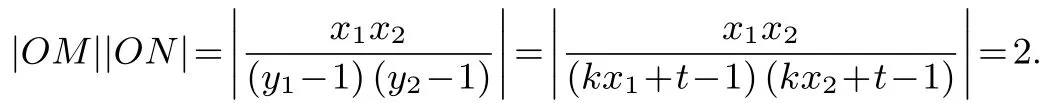
可得t=0，即直线l经过原点.

例2(2019年高考全国ⅠⅠ卷理科第21 题)已知点A(-2,0),B(2,0)，动 点M(x,y)满足直线AM与BM的斜率之积为记M的轨迹为曲线C.

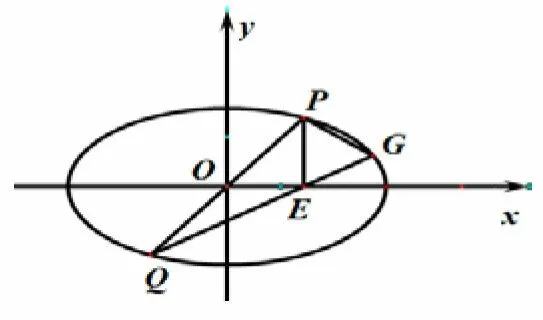
图2

(1)求C的方程，并说明C是什么曲线;

(2)过坐标原点的直线交C于P,Q两点，点P在第一象限，PE ⊥x轴，垂足为E，连结QE并延长交C于点G.(i)证明： ∆PQG是直角三角形;(ii)求∆PQG面积的最大值.

解析(1)

共性分析这两个例题情境都是直线过椭圆的中心，问题形式中都满足a2= 2b2.事实上，这都基于椭圆的一条性质： 若过椭圆中心O的直线与椭圆相交于A,B两点，C为椭圆上异于A,B的任一点，则直线CA与CB的斜率之积为

从例2 证明过程可以看到，kP Q= 2kQG，只有椭圆= 1 (a ＞ b ＞0)满足a2= 2b2时，才有PQ ⊥PG，这就是为什么例2中要设定椭圆方程为同 样 在 图1中，由且|OA|=b= 1，所以|OM||ON|= 2，这恰是例1 中之所以要设定椭圆方程为的原因.

二、试题解法中的共性研究

研究高考题肯定避免不了研究其解法，把高考题作为例题进行选讲，要充分发挥它解法的基础性、示范性、典型性.因此很有必要从不同的高考题中提炼解法的典型性和共性，甚至有时候一道试题的命制就是基于这种解法的共性，比如例1 与2019年高考数学北京卷理18 题.

例3(2019年高考北京卷理科第18 题)已知抛物线x2=-2py经过点(2,-1).

(1)求抛物线C的的方程及其准线方程.

(2)设O为原点，过抛物线C的焦点作斜率不为0 的直线l交抛物线C于两点M,N，直线y=-1 分别交直线OM,ON于点A和B.求证以AB为直径的圆经过y轴上的两个定点.

解析(1)x2=-4y,y=1.

(2)设直线l的方程为y=kx-1，0，代入抛物线方程可得x2+4kx-4 = 0.设M(x1,y1),N(x2,y2)，则x1+x2=-4k,x1x2=-4.直线OM,ON的方程分别为所以以AB为直径的圆的方程为+(y+1)(y+1)=0，化简为

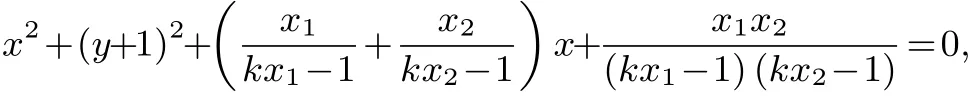
共性分析例1 与例3 解法中都基于直线l:y=kx+t与圆锥曲线交于两点(x1,y1),(x2,y2)，再连接这两点和圆锥曲线某顶点的连线与另一条固定直线相交于新的两点.因此，例3 中的“圆过定点”与例1 中的“直线过定点”的关键原因就是： 例3 中两点和横坐标满足为定值;例1 中两点M,N横坐标在条件“|OM||ON|= 2”下也满足为定值.所以这两题就是“在为定值的条件下求解”的问题(其中λ为与圆锥曲线某顶点坐标相关的实数)，这也是这两道高考题的解法共性所在.

三、试题变式中的共性联系

著名数学教育家波利亚说过，好问题同种蘑菇类似，它们都成堆生长，找到一个以后，你应当在周围再找一找，很可能附近就有几个.那么基于试题共性的基础上，你会发现对试题进行变式，就是最好的一种“找蘑菇”的方式.这种方式可以根据事物内部的联系，交换或改变条件，就会产生另外一种结论.比如，例1 与例3 之间基于共性分析在题干不变情况下，变化“为定值”的关键条件，例1 与例3 就能基于共性构建相关联系.

例4(例3 变式)已知抛物线C:x2=-2py经过点(2,-1).

(1)求抛物线C的方程及其准线方程.

(2)设O为原点，作斜率不为0 的直线l交抛物线C于两点M,N，直线y=-1 分别交直线OM,ON，x轴于点A,B,H.若|HA|·|HB|=2，直线l是否经过定点?

解析(1)x2=-4y,y=1.

(2)设直线l的方程为y=kx+t,(k0)，代入抛物线方程可得x2+4kx+4t= 0.设M(x1,y1),N(x2.y2)，则x1+x2=-4k,x1x2=4t.所以H(0,-1)，所以|HA||HB|=2，解得t=±2，即直线l是经过定点(0,2)或(0,-2).

例5(例1 变式)已知椭圆的右焦点F(1,0)，且经过A(0,1).

(1)求椭圆C的方程;

(2)O为原点，直线l:y=kc+t(1)与椭圆C交于两个不同的点P,Q，直线AP与x轴交于点M，直线AQ与x轴交于点N，那么以MN为直径的圆是否过y轴上定点?

解析(1)

(2)设P(x1,y1),Q(x2,y2)，则以MN为直径的圆方程为将l:y=kx+t代入椭圆方程得(2k2+1)x2+4ktx+2t2-2=0，则

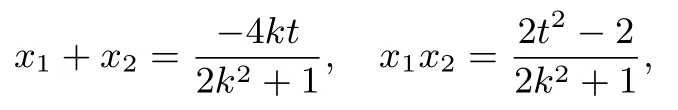
评注上述变式中，例4 中加入条件“|HA||HB|= 2”即保证了“为定值2”可得到具体的t值; 例5 中虽然去掉了条件“若|OM||ON|= 2”，但依然为关于t的定值.所以通过这种内部联系改变条件使得例1 与例3 的结论相互转化.

四、试题设问中的共性研究

有时候两道解析几何高考题之间的问题情境和问题设问的形式上没有直接关联，但如果抓住交互的知识点，通过数学抽象对高考题的设问进行共性研究，就能抓住数学问题的本质，形成解决问题的思路，比如浙沪卷的解析几何题.

例6(2019年高考浙江卷第21 题)如图3，已知F(1,0)是抛物线y2= 2px(p ＞0)的焦点，过点F的直线交抛物线于A,B两点，点C在抛物线上，使得∆ABC的重心G在x轴上，直线AC交x轴于点Q，点Q在点F的右侧，记∆AFG，∆CQG的面积分别为S1,S2.

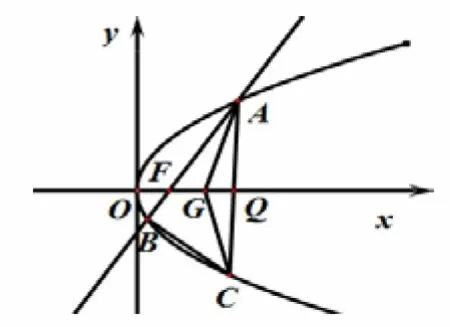
图3

(1)求p的值及抛物线的准线方程;

解析(1)p=2,x=-1;

(2)设A(t2,2t)(t0)，直线AB方程为1 代入抛物线方程为所 以联立重心坐标公式得

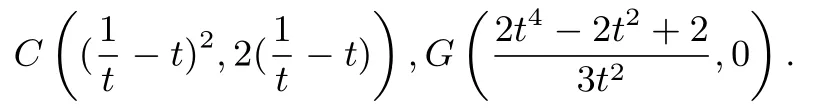
所以AC方程为y-2t=2t(x-t2)，得Q(t2-1,0)，由于Q在点F的右侧，则t2＞2.则

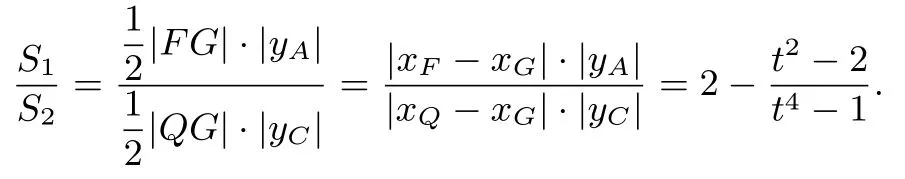
令m=t2-2，则

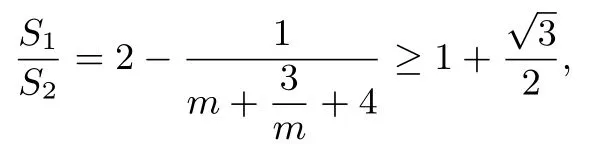
此时G(2,0).

例7(2019年高考上海卷第20 题)如图4，已知椭圆，F1,F2为其左、右焦点，直线l过F2且与椭圆交于A,B两点.

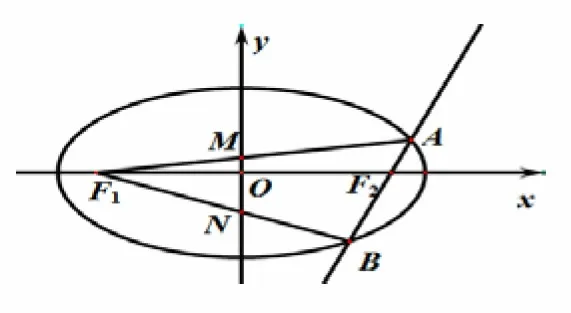
图4

(1)AB垂直于x轴时，求

(2)若∠F1AB= 90°，且A在x轴上方，求A,B两点的坐标;

(3)直线AF1交y轴于M,BF1交y轴于N，问： 是否存在直线l使得S∆F1AB=S∆F1MN，若存在求出直线l的方程;若不存在，请说明理由.

解析(1)

(2)A(0,2),

(3)设直线AB的方程为x=my+c，A(x1,y1),B(x2,y2)，将直线方程代入椭圆方程得(m2+2)y2+4my-4=0，所以

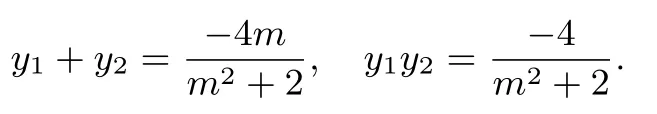
直线AF1为所以同理

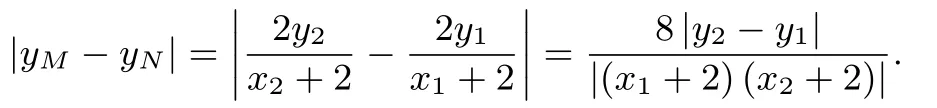
由S∆F1AB=S∆F1MN得|yM - yN|= 2|y2- y1|解得故存在

共性分析若从面积比值的这个交互点来看，两道高考题的设问本质是一样的.如果例6 第(2)问中记则此时就是时，求G点坐标; 例7 第(3)问中若记S∆F1AB=S1,S∆F1MN=S2，令则此时就是λ= 1 时，求直线l的方程.因此，例4 与例5 设问本质上就是圆锥曲线中关于三角形面积比值的问题.因此，在解题思路上也是大同小异! 例6 第(2)问中，由最终转化为A点纵坐标、Q点坐标及G点坐标计算上面来;例7第(3)问中由S∆F1AB=S∆F1MN转化为利用韦达定理对点M,N,A,B，的纵坐标进行运算.只是例6 在计算时需从设“A点”坐标开始较为方便，而例7 可直接设直线方程代入椭圆方程计算.

五、结语

唯物辩证法认为，联系具有多样性，有直接联系和间接联系，内部联系和外部联系，本质联系和非本质联系，必然联系和偶然联系、整体与部分的联系等，我们在高考备考中研究高考试题时，可以根据联系的多样性，对各地高考试卷考点进行归纳与分类，寻找联系之间的共性.美国数学家Halmos 说过，“数学研究主要就是发现问题和解决问题”，实践表明，在发现问题和解决问题过程中，很多高考题都能通过归纳与分类的方式和基于联系观，在情境与问题、在问题立意和问题本质上中找到共性.对这些共性研究更能抓住问题的本质，更有利于基于共同的情境、分析数学问题的变式和拓展，引发学生思考与交流，形成和发展数学学科核心素养.