一道几何赛题的若干证法
2020-02-20广东省深圳中学518001邱际春
广东省深圳中学(518001) 邱际春
广东省深圳市桂园中学(518008) 罗 芳
2019年广东省中学生数学夏令营高中联赛模拟试题二试中有如下一道几何题:
题目如图1,在凸四边形ABCD的边BC,AD上分别取点E,F,满足以E为圆心过点B的圆与直线CD相切,以F为圆心过点A的圆与直线CD相切,证明: 直线AB,EF,CD平行或交于一点的充要条件是∠A=∠B.
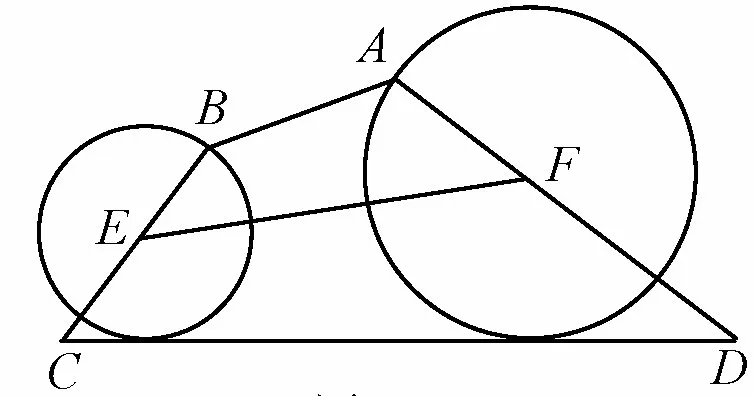
图1
本题以四边形、圆为背景,考查三线共点与三点共线之间的转化能力,是一道方法多样、综合性较强的试题.下面是广东省数学会给出的参考解答:
证明如图2,设直线BC与直线AD交于点G,直线AB与直线FE交于点H(若平行时视为交于无穷远点),则
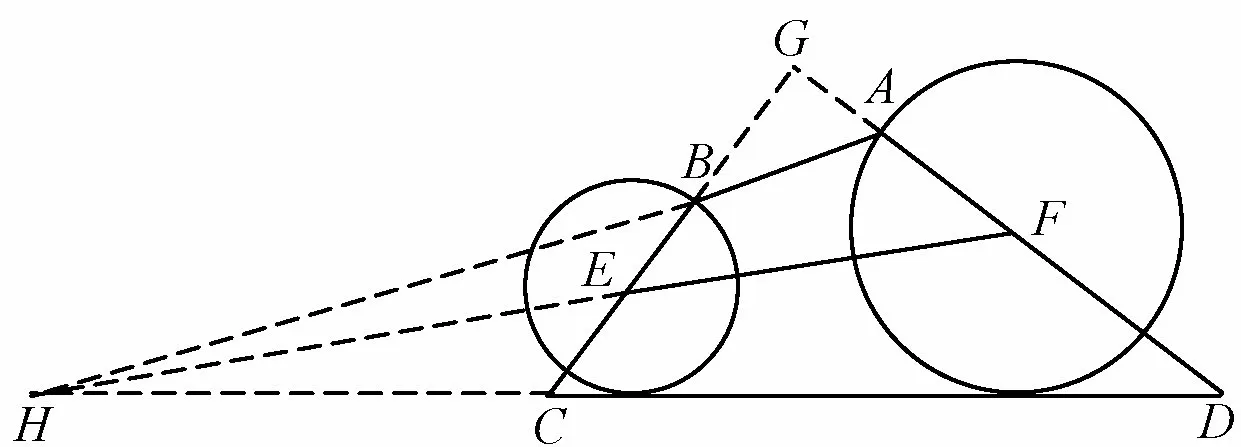
图2
根据梅涅劳斯定理及其逆定理可知,直线AB,EF,CD平行或交于一点⇔H,C,D三点共线又直线HA截∆GEF,于是由梅涅劳斯定理知比较上述两式可得
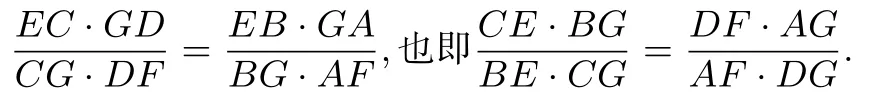
设直线CD与⊙E,⊙F的切点分别为M,N,连接EM,FN,则BE=EM=CE ·sin ∠C,AF=FN=DF ·sin ∠D.将此两式代入上式,得所以从而
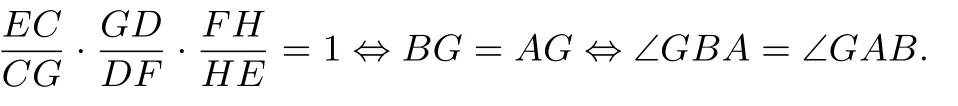
因此,直线AB,EF,CD平行或交于一点的充要条件是∠A=∠B.
评注若从题目中包含的基本图形来看,此题似乎由《近代欧氏几何学》中第13 页的定理[1]演变而来,将两圆看成位似形还可进一步推出一些好的结论.
接下来,笔者拟从相似、面积、位似、根轴等角度进行探究,给出下面几种证明方法.
另证一如图3,不妨设直线AB与直线EF相交于H(若平行时视为交于无穷远点),与⊙E交于一点L,直线CD分别与⊙E,⊙F切于点M,N,则直线AB,EF,CD交于一点⇔H,C,D三点共线.
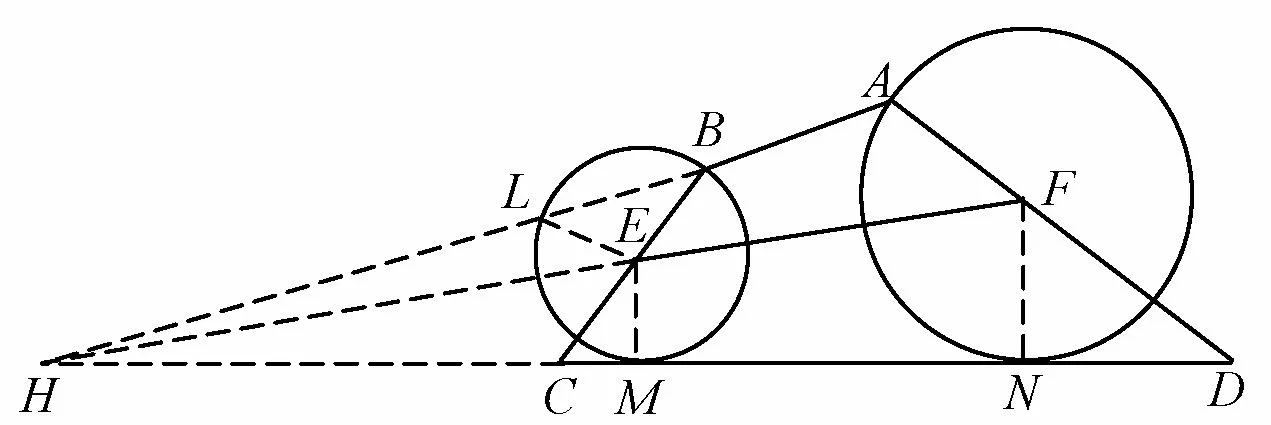
图3
注意到H,C,D三点共线⇔ H,M,N三点共线⇔∠FHM= ∠FHN.下面只需证明∠ABC= ∠BAD ⇔∠FHM=∠FHN.
因为EL=EB,所以∠BLE=∠LBE.又因为
∠LBE+∠ABC=180°,∠BLE+∠HLE=180°.
所以∠ABC=∠HLE,所以
∠ABC=∠BAD ⇔∠BAD=∠HLE ⇔∆LHE∽∆AHF.
因为EM ⊥ CD,FN ⊥ CD,所以EM ‖ FN,所以∠HEM=∠HFN.又注意到LE=EM,AF=FN,于是
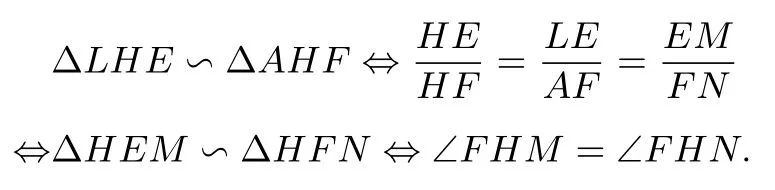
故∠ABC=∠BAD ⇔∠FHM=∠FHN.
综上所述,直线AB,EF,CD平行或交于一点的充要条件是∠A=∠B
另证二如图4,不妨设直线AB与直线EF相交于H(若平行时视为交于无穷远点),连接AE,BF,直线CD分别与⊙E,⊙F切于点M,N,过点E作EG ⊥AB于点G,过点F作FK ⊥AB于点K,则直线AB,EF,CD交于一点⇔H,C,D三点共线.

图4
注意到H,C,D三点共线⇔ H,M,N三点共线⇔∠FHM= ∠FHN.下面只需证明∠ABC= ∠BAD ⇔∠FHM=∠FHN.
因为EM ⊥ CD,FN ⊥ CD,所以EM ‖ FN,所以∠HEM= ∠HFN.从而H,M,N三点共线⇔∆HEM∽∆HFN ⇔又因为∠HGE=∠HKF,∠GHE= ∠KHF,所以∆GHE∽∆KHF,所以因为
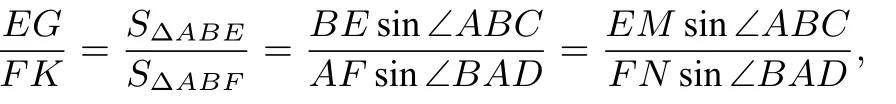
H,M,N三点共线
综上所述,直线AB,EF,CD平行或交于一点的充要条件是∠A=∠B.
另证三如图5,设直线AB与直线FE交于点H(若平行时视为交于无穷远点),连接HC和HD,则直线AB,EF,CD平行或交于一点⇔H,C,D三点共线.
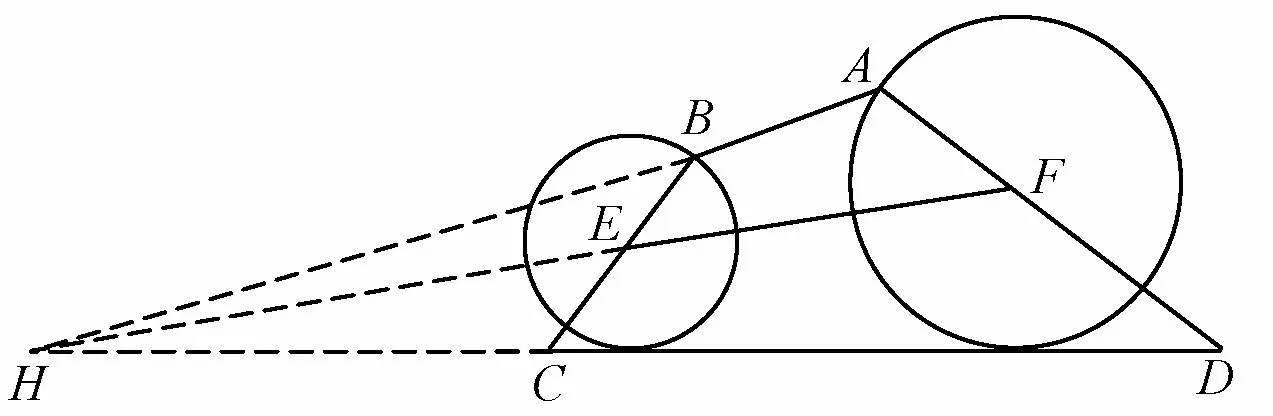
图5
注意到
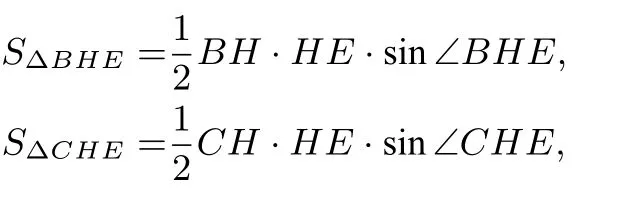
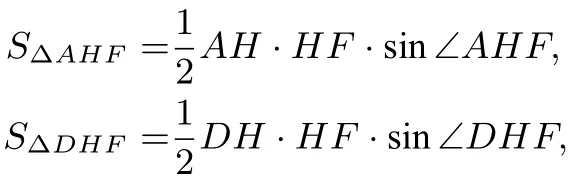
分别代入上述等式可得
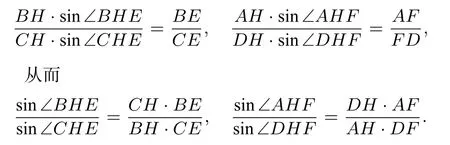
由正弦定理可知
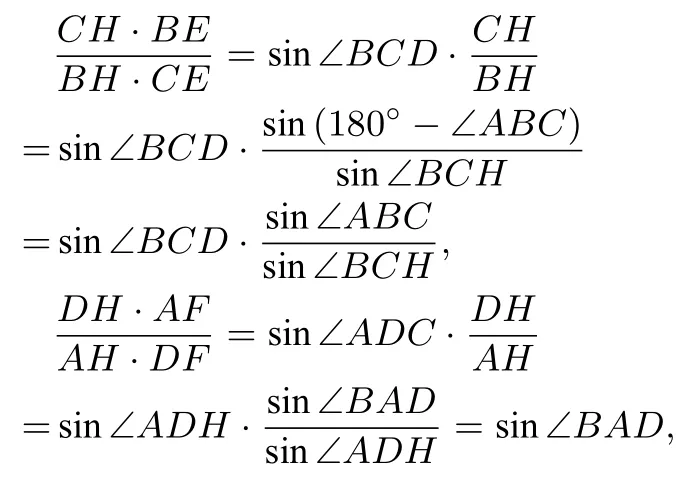
又由于
H,C,D三点共线⇔sin ∠BCD=sin ∠BCH
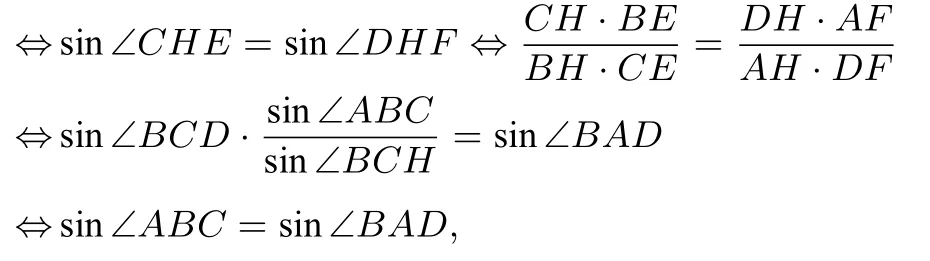
故∠ABC=∠BAD.
因此,直线AB,EF,CD平行或交于一点的充要条件是∠A=∠B.
另证四如图6,设直线EF与直线CD交于点H(若平行时视为交于无穷远点),连接AH分别交⊙E于点L,B′,连接B′E,直线CD分别与⊙E,⊙F切于点M,N,则EM ⊥CD,FN ⊥CD.
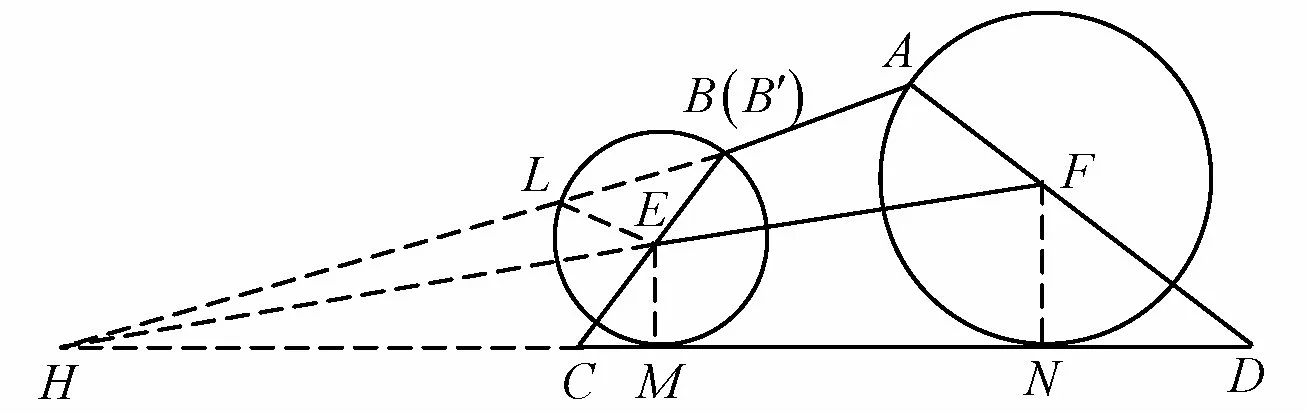
图6
因为∠EHM= ∠FHM,所以∆EHM∽∆FHN.记⊙E的半径为r,⊙F的半径为R,则设是以H为位似中心,为位似比的位似变换.则在的变换下,M → N,E → F,L →
A,∆HEM →∆HFN,∆HLE →∆HAF.
先证充分性:根据位似的性质,有LE ‖ AF,故∠HLE=∠HAF.又因为∠ELB′=∠LB′E,所以
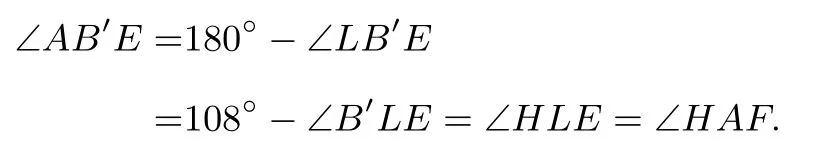
因为∠ABE=∠BAF,所以点B′与点B重合.故三条直线AB,CD,EF平行或交于一点.
再证必要性: 由于三条直线AB,CD,EF交于一点H(若平行时视为交于无穷远点),根据位似的性质,有∠HLE=∠HAF,又因为∠ELB=∠LBE,所以
∠ABE=180°-∠LBE=180°-∠BLE=∠HLE.故∠ABC=∠BAD.
因此,直线AB,EF,CD平行或交于一点的充要条件是∠A=∠B.
另证五如图7,设直线CD分别与⊙E,⊙F切于点M,N,直线EF分别与⊙E,⊙F交于点P,Q,分别连接EM,FN,BM,BP,PM,AN,AQ,QN,则有

图7
∠EMN= ∠FNM= 90°,∠EPM= ∠EMP,∠FQN=∠FNQ,∠EBP= ∠EPB,∠FAQ= ∠FQA.因 为∠MEF+∠EFN=180°,即

所以∠EPM+∠FNQ=90°,所以

所以P,Q,M,N四点共圆.
先证充分性: 在四边形ABEF中,有∠ABE+∠BEF+∠AFE+∠BAF=360°,又由于
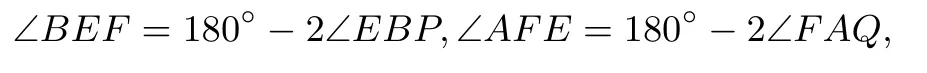
代入上式整理可得
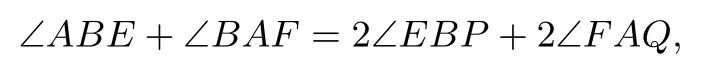
因为∠ABC=∠BAD,所以
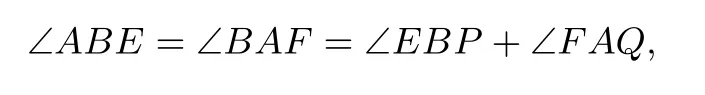
所以∠ABP= ∠ANF,所以A,B,P,Q四点共圆.因为∠FAN=∠FNA,所以

所以
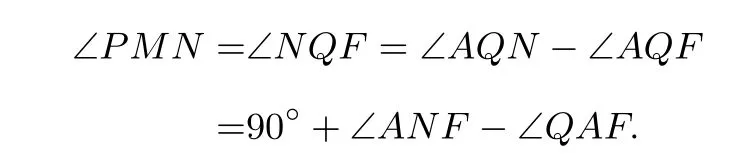
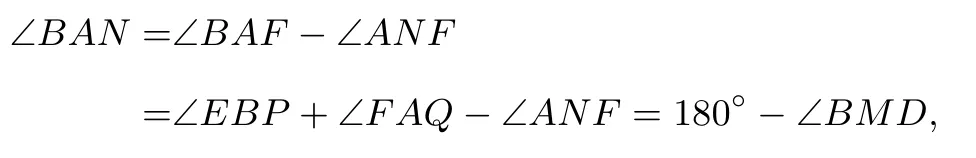
所以A,B,M,N四点共圆.考虑四边形ABPQ,四边形ABMN,四边形PQMN的外接圆,其两两的根轴分别为直线AB,CD,EF.故由根心定理知,这三条直线AB,CE,EF交于这三个圆的根心H或平行.
再证必要性: 设三条直线AB,CD,EF交于点H(若平行时视为交于无穷远点),∆BMN的外接圆交直线AB于点A′,则A′,B,M,N四点共圆.由圆幂定理得HA′ ·HB=HM ·HN,又因为P,Q,M,N四点共圆,有HP ·HQ=HM ·HN,所以

由圆幂定理的逆定理可知A′,B,P,Q四点共圆,所以∠BA′Q=∠BPE.
因为∠BMN=180°+∠FAN-∠BAQ-∠QAF,所以∠BA′N=∠BA′Q+∠QAF-∠FAN=∠BA′Q+∠QAN,所以∠QA′N=∠QAN,所以A,A′,Q,N四点共圆.
因为∠BAN= 180° -∠BMN >90°,所以点A′与A重合.因为A,B,P,Q四点共圆,所以∠EPB=∠BAQ,∠ABP=∠AQF,两式相加得∠ABP+∠EPB=∠BAQ+∠AQF,即∠ABP+∠EBP=∠BAQ+∠QAF,所以∠ABC=∠BAD.
