外包环境下格上可撤销的属性基加密方案*

于金霞，杨超超，张棋超，闫玺玺

河南理工大学 计算机科学与技术学院，河南 焦作 454000

1 引言

2005年，Sahai和Waters[1]在欧洲密码学会上提出了属性基加密（attribute-based encryption，ABE）的概念，它用一系列属性来表示用户的身份，并在选择身份安全模型下完成了对方案的证明。2006年，Goyal等人[2]根据加密策略的不同将ABE体制分为密钥策略属性基加密（key-policy attribute based encryption，KP-ABE）和密文策略属性基加密（ciphertext-policy attribute based encryption，CP-ABE）。与传统的公钥加密机制相比，属性基加密具有用户的动态性、访问策略的灵活性以及用户身份的隐私性等优点。这些特点使属性基加密机制满足当前大数据时代的需求。为了更好地存储数据、管理数据和共享数据，数据拥有者可以将大量的密文数据给外包服务提供商，由外包服务提供商来存储和管理外包的数据，并为数据使用者提供服务。而属性基加密系统应用中，用户或用户的属性会发生改变，因此属性撤销或更新是一个值得深入研究的问题。

针对上述问题，许多可撤销的属性基加密被提出。何倩等人[3]将属性分为动态和静态属性，提出支持动静态属性撤销的CP-ABE方案。Nomura等人[4]提出一种可撤销的多机构CP-ABE方案，不需要为撤销属性的用户更新密钥。闫玺玺等人[5]提出一种支持用户撤销的CP-ABE方案，同时采用半策略隐藏方式实现隐私保护。Xu等人[6]提出一种云环境下支持细粒度访问控制的可撤销KP-ABE方案，为云中动态用户组提供数据共享。王光波等人[7]利用云存储中心实现属性撤销，提出云存储环境下支持撤销的CPABE方案。Liu等人[8]提出一种支持解密外包和属性撤销的CP-ABE方案，将一些解密计算任务外包给云服务器。赵等人[9]设计出一种无密钥托管支持撤销的CP-ABE方案，使用属性版本密钥来实现属性撤销。Liu等人[10]提出支持解密外包、属性撤销和策略更新的CP-ABE方案，通过实验证明了方法的有效性和实用性。闫玺玺等人[11]设计了数据外包环境下一种支持撤销的属性基加密方案。上述方案大多是建立在双线性对基础上的，加解密过程中需要多次双线性对运算，存在计算复杂度较高且无法抵抗量子攻击等问题。基于格的密码体制被认为是可以抵抗量子攻击的，因此近年来基于格论构造的加密方案受到广泛关注。Boyen[12]提出格上第一个属性基加密方案，基于线性秘密共享技术（linear secret sharing schemes，LSSS）提出KP-ABE方案，由于该方案采用了通过矩阵级联方式构造的大维数虚拟加密矩阵，使得效率不高。Wang[13]提出了格上支持多值属性的属性基加密方案，方案采用陷门生成算法及抽样算法构造，通过“与”操作实现访问控制。针对属性撤销问题，张欣威等人[14]提出采用二叉树实现格上属性撤销的CP-ABE方案，但是该方案仅支持门限访问结构，不支持属性的即时撤销。Wang等人[15]也利用二叉树设计了格上支持撤销且具有灵活访问结构的CP-ABE方案，但不支持属性的即时撤销。

本文针对已有的格上可撤销的属性基加密方案的不足，结合闫玺玺等人[11]提出的CP-ABE方案，设计出一种外包环境下格上可撤销的密文策略属性基加密方案，借助数据外包管理服务器，实现属性的即时撤销。同时，方案采用访问树结构，实现细粒度的访问策略，表达方式更加灵活。

2 相关知识

2.1 格和格上困难问题

定义1（格）Rm上n个线性无关的向量b1,b2,…,bn由这些向量线性组合构成的向量集合定义为格Λ，即格其中向量组b1,b2,…,bn构成格Λ的一组格基B。

定义2（q-元格）设q是素数，定义q-元格：

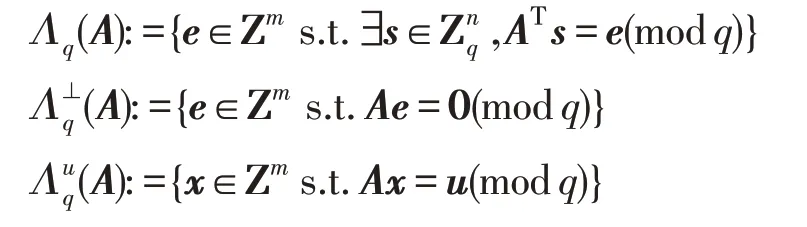
定义3（高斯参数）对任意s＞0，以向量c为中心，s为参数的格Λ上的离散高斯分布为，其中ρs,c(x)=exp(-π||x-c||2/s2)本文中||∙||表示欧几里德范数，即二范数。

定义4（判定性误差学习问题（decisional learning with error，D-LWE））令q为一素数，n为正整数，对于任意α＞0，定义Ψα是一正态分布，其中心为O方差为为Ψα在Zq上的离散分布LWE问题实例是指：对于，判断挑战模型O是随机采样机还是伪随机采样机Os。Os和有如下特征：

Os：输出带噪声的伪随机样本，其中是密钥，是均匀向量，xi是离散分布χ上的噪声。

(Zq,n,)-LWE问题允许重复询问挑战模型O，挑战模型O随机利用Os和为敌手生成若干采样样品(ωi,vi)，如果对于任意，敌手可以区分样品来自Os或的优势是可忽略的，则敌手可以解决判定性(Zq,n,)-LWE问题。

2.2 重要算法

引理1TrapGen(q,n)：对于q=poly(n)，n为正整数，m≥5nlbq存在概率多项式时间算法TrapGen(q,n)生产均匀随机矩阵，其中ΤA是格的陷门基，且。

引理2SampleLeft(A,B,ΤA,u,σ)：

输入：秩为n的矩阵，矩阵，格的陷门基，向量和高斯参数。

输出：令F=A|B，则算法输出向量，满足F∙e=umodq。

引理3SampleRight(A,B,R,u,σ)：

输出：令F=A|AR+B则算法输出向量满足F∙e=umodq。

3 方案定义和安全模型

3.1 数据外包系统架构

传统的数据外包系统如图1所示，包括可信属性授权机构、数据管理服务器、数据服务器、数据拥有者和数据使用者五部分。

Fig.1 Data outsourcing system architecture图1 数据外包系统架构

（1）可信属性授权机构：生成系统的主公钥和主私钥，以及根据用户的属性为用户生成私钥。同时负责属性的更新和撤销。

（2）数据管理服务器：统一管理外包的数据，对请求访问的用户实现访问控制。

（3）数据服务器：存储外包的数据。

（4）数据拥有者：对数据进行加密，设置密文的访问策略，将密文上传到数据服务器，由数据管理服务器对数据密文进行管理。

（5）数据使用者：对数据服务器上的数据进行申请和正常的访问。

3.2 算法定义

本方案包括如下7个步骤：

系统初始化Setup(1λ)：输入安全参数λ、属性域R，输出公钥PK、主私钥MSK。

密钥生成KGen(PK,MSK,ω,U) 输入公共参数PK主私钥MSK、属性集合ω、用户集合U，得到用户的属性私钥SKω。

密钥加密密钥生成KEKGen(U)：输入用户集合U，输出用户的二叉树KEK。

数据加密Enc(PK,M,T)：输入公共参数PK、消息M、访问树T，输出密文C。

数据重加密ReEnc(C,U)：输入密文C、属性用户集合U，输出重加密后的密文C'和头部信息Hdr。

属性群密钥解密UkDec(Hdr.KEK)：输入头部信息Hdr用户的二叉树KEK输出属性用户群密钥Ki

数据解密Dec(C',SK,PK) 输入重加密后的密文C'用户的私钥SKω、公共参数PK输出明文消息M

3.3 安全模型

格上属性基加密方案的安全性需满足选择属性及选择明文攻击下的不可区分性。本方案采用Agrawal等人[16]提出的格上ABE方案的安全模型进行安全性证明，文献[13]也是基于该安全模型证明的。安全模型由一个模拟器和一个敌手组成，具体游戏过程如下。

初始化：敌手选择将要挑战的访问树T∗，然后交给模拟器。

系统设置：模拟器用Setup(1λ)算法，得到公共参数PP和系统的主私钥MSK然后将PP发送给敌手。

阶段1敌手询问任何不满足访问树T∗的属性集合的私钥。依据敌手提交的询问，模拟生成属性集合私钥SK，并运行KEKGen(U)算法计算用户的二叉树KEK，将它们传给敌手。

挑战：敌手选择明文M0,M1∈{0,1}，并将其发给挑战者B模拟器挑战者随机选取b∈{0,1} 通过Enc(PK,Mb,T)算法和ReEnc(C,U)算法计算出挑战密文C'和头信息Hdr返给攻击者D并将其发送给敌手。

阶段2同阶段1。

猜测：敌手提交对b的猜想b'。

若无攻击者在概率多项式时间内以不可忽略的优势赢得此游戏，则方案支持选择属性和选择明文攻击下不可区分性的安全性。

4 方案构造

4.1 系统初始化

Setup(1λ)：输入安全参数λ，属性域R，生产公钥PK和主私钥MSK。

（1）授权机构利用陷门生成算法TrapGen(1λ)，生成一个均匀随机矩阵和格的满秩短基

（2）为每个属性i∈R，随机生成矩阵；

4.2 密钥生成

KGen(PK,MSK,ω,U)：输入公共参数PK、主私钥MSK、属性集合ω、用户集合U，输出用户属性私钥SKω。

用户请求获得密钥，认证机构为其生成用户属性私钥。

（1）对于每个属性i∈ϖ，令计算

（2）输出用户私钥SKω=(ei)i∈ω。

记录每个属性i∈R相应的属性用户群为Ui，并将其交给数据管理服务器。

4.3 密钥加密密钥生成

KEKGen(U)：输入属性用户群U，输出用户的二叉树KEK。

（1）数据管理服务器根据用户数量生成二叉树，树中每个叶子节点表示一个用户。为树中的每个节点Vj随机生成一个密钥KEKj。Path(ut)表示从二叉树的代表用户ut的节点到根节点所经过的路径节点集合，记为用户ut的路径密钥。

（2）存在一个最小集合可以包含属性用户群Ui，记为KEK(Ui) 如图2，假设存在4个用户{u1,u2,u3,u4}属性用户群Uj={u1,u2,u3} 则KEK(Uj)={KEK2,KEK6}。

Fig.2 KEK binary tree图2 KEK二叉树

4.4 加密

数据拥有者获取公共参数PK，根据访问树T，通过Enc(PK,M,T)算法加密消息M。

（1）随机选择s←，再选择一个高斯误差分布χ并从中选择误差参数x0并计算

（2）访问树的根节点的值设为s，标记为已分配，其他所有节点标记为未分配。访问树的叶子节点代表属性。从上到下对树中未标记的非叶子节点运行如下递归算法。

若该节点为∧操作，并且该节点的子节点未赋值，则为其孩子节点赋值一个随机数sk，满足，并标记为已分配。若该节点为∨操作，且其孩子节点为未分配，则其孩子节点赋值为s，并标记为已分配。若叶子节点对应的属性为i，则记其对应的值为si。从高斯误差分布χ中选择x1,x2∈随机选取R1,i,R2,i∈{-1,1}m×m计算

4.5 数据重加密

数据重加密ReEnc(C,U)输入密文C，属性用户集合U，输出重加密后的密文C'和头部信息Hdr。

（1）数据管理服务器接受密文后，对密文进行重加密处理。随机选择一对互逆向量Fi和，计算，则密文

（2）选择对称加密算法Ek(x)，其中k为密钥，x为明文。生成头信息

当用户向数据管理服务器发送使用请求时，数据管理服务器将(Hdr,C')发送给用户。

4.6 数据解密

数据解密阶段，先进行属性群密钥解密，再进行数据解密。

用户先进行属性群密钥解密UkDec(Hdr.KEK)：输入头部信息Hdr，用户的二叉树KEK，解密头信息得到，并更新用户自己的私钥

然后进行数据解密Dec(C',SK,PK)。选择满足访问树的最小属性集合记为ω'，计算：

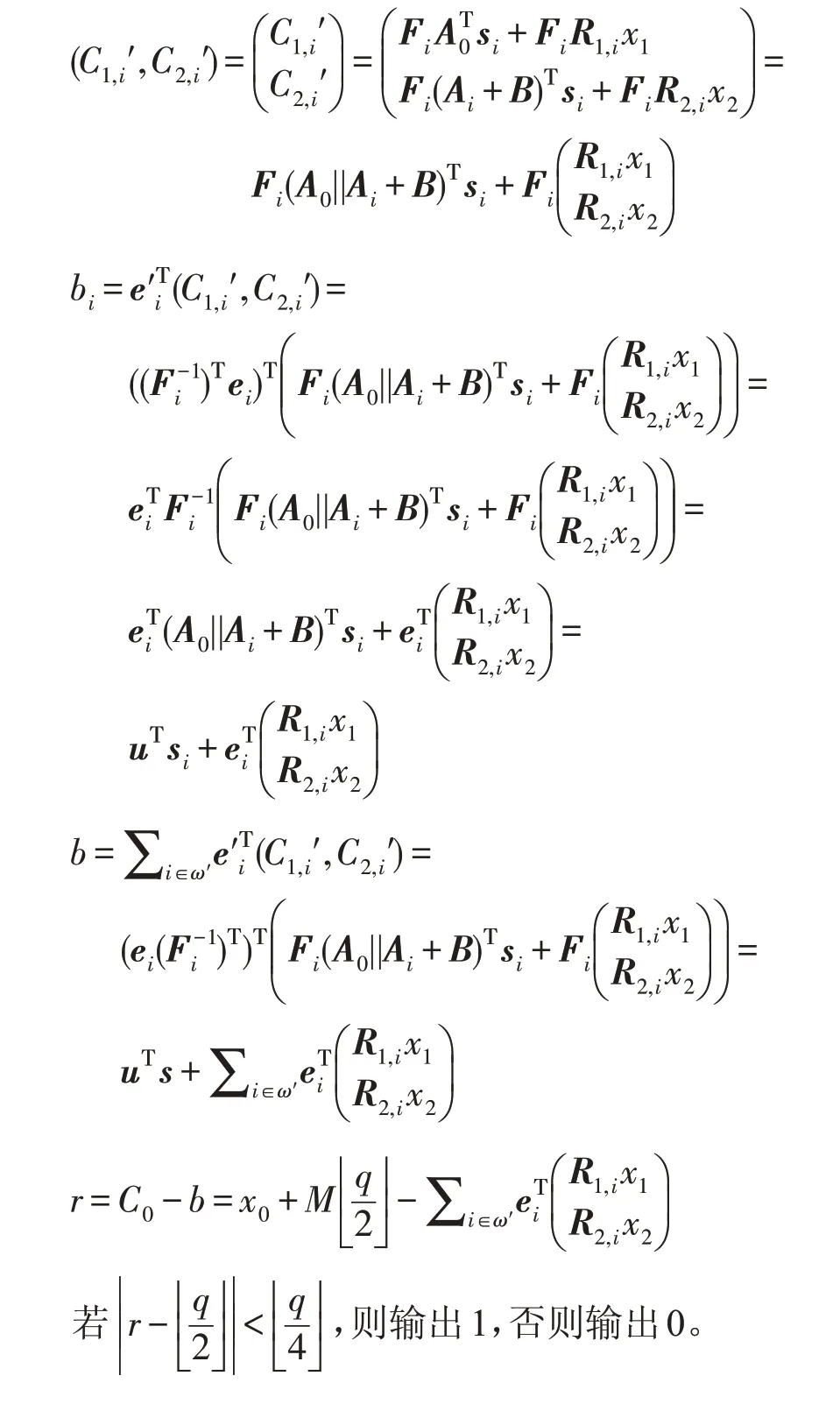
5 方案分析

5.1 正确性分析

用户的属性发生改变后，数据管理服务器对属性群密钥进行更新。用户收到数据管理服务器发送更新后的(Hdr',C″) 并更新自己的私钥，然后对密文进行解密，对于i∈f，有：

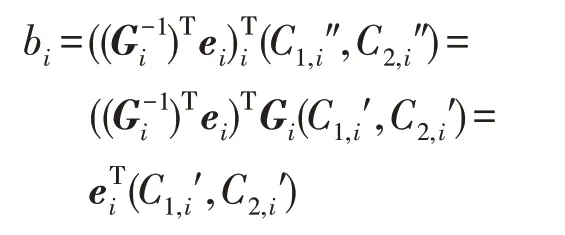
对于i∉f，因此对于i∈ω bi=。在解密时，更新的密钥和未更新的密钥运算方式相同，解密算法能够正常解密。

5.2 安全性证明

初始化：敌手D选择要攻击的访问树T，把其交给挑战者B。

设置：挑战者B收到T后：

（1）挑战者访问LWE采样预言机O获得样本

（2）使用陷门生成算法TrapGen(n,q)生成(B,ΤB)。

（3）对于i∈T随机选择Ri∈{-1,1}m×m，计算Ai=ARi-B；对于i∉T，随机选择Ri∈{-1,1}m×m，计算Ai=ARi。

最终，挑战者B给敌手D返回公共参数PK=(A,B,{Ai}i∈T,u)，保留(ΤB,{Ri}i∈T,v0,vu)。

阶段1敌手D可以询问不满足访问树T的属性集ω。挑战者B接收敌手D的询问，然后运行算法SampleRight(A,B,Ri,ΤB,σ,u)→ei，得到敌手属性私钥SKω=(ei)i∈ω。用KEKGen(U)算法计算出用户的二叉树KEK。挑战者B把属性私钥SKω和KEK交给敌手D。

挑战：敌手D选择明文M0,M1∈{0,1}发给挑战者B。挑战者随机选取b∈(0,1)，对Mb进行加密，计算，得到密文C=(C0,{C1,i,C2,i}i∈ω)。随机选择一对互逆向量Fi和，计算，对密文进行重加密处理，得到。选择对称加密算法Ek(x)，其中k为密钥，x为明文，生成头信息Hdr=。挑战者B将密文C'和头信息Hdr返给攻击者D。

阶段2同阶段1。

猜测：敌手提交对b的猜想b'。模拟器根据敌手对b的猜想b'挑战定义4中的LWE问题，如果b'=b，则输出O=Os此时敌手的优势Pr[b'=b|O=Os]=1/2+ε如果b'≠b则输出O=Os' 此时敌手的优势Pr[b'≠b|O=Os']=1/2因此敌手能以可忽略的优势区分密文C'和Zq上的均匀随机分布，也就是说敌手若能以不可忽略的概率猜出b则可以以相同的优势解决(Zq,n,)-LWE问题。

5.3 性能分析

将本文方案从访问结构、公钥长度、私钥长度、密文长度、是否支持属性撤销以及是否支持属性即时撤销等方面与相关方案进行对比，如表1。其中q、n、m为格上的相关参数（根据引理1中定义规定，m≥5nlbq），s代表系统属性总数量，Au代表用户属性的数量，Ac代表加密时使用的属性数量。t表示解密时所需的最小属性集合中属性的个数，O表示计算复杂度。

从表1可以看出，本文方案比文献[13-14]少了nmlbq，比文献[15]少了4snmlbq+(2s-2m-1)nlbq，由于s代表系统属性总数量，值较大，因此本文方案公钥长度有了明显的缩短。用户私钥长度方面，本文方案和文献[13]保持一样，是文献[14-15]私钥长度的50%。密文长度方面，文献[13]仅和m相关，和加密访问策略属性无关，达到了最优的长度，但其功能方面并未考虑属性撤销。和文献[15]相比，本文方案密文长度具有明显的优势，缩短了(Ac+1)lbq。与文献[14]具有相同的密文长度，但本文方案支持属性的即时撤销。因此，结合公钥长度、私钥长度、密文长度等参数，本文方案在通信代价方面具有优势。

Table 1 Comparison of related papers表1 相关方案对比

功能方面，文献[13]不支持属性撤销，文献[14-15]和本文方案支持属性撤销，但是文献[14-15]不支持属性的即时撤销，本文方案支持属性的即时撤销。访问结构上，文献[13-14]都采用门限访问结构，访问结构表达不够灵活。文献[15]采用析取范式访问结构，本文方案采用访问树结构，都支持更为灵活的访问策略。

综上，本文所提出的方案在性能方面得到了很大的提升，在功能方面更加完善，支持属性的即时撤销，更加满足外包环境中的应用需求。

6 结束语

本文提出一种外包环境下格上可撤销的密文策略属性基加密方案。方案采用访问树结构，访问策略更灵活。同时，方案实现了属性即时撤销，满足社交网络平台等云环境的应用需求。方案被证明满足选择属性及选择明文攻击下安全。基于理想格的加密方案具有更高的加解密效率，下一步将对构造基于理想格的高效可撤销属性基加密方案进行研究。