基于Kriging方法和Pettitt检验的数据冲突判别

李建勋，唐子豪，张永进，王小江

西安理工大学，西安710054

1 引言

随着大数据时代的来临，数据价值与数据质量获得了人们的广泛关注，然而由于人员疏忽、自然灾害、设备故障、采集环境条件限制、数据录入违反规则等原因，数据缺失、数据冗余、数据延时、数据错误、数据冲突等现象时有发生。在这一系列数据问题中，数据冲突是标示同一实体对象的多个数据间明显差异所形成的不可调和矛盾，它包括数据结构冲突、数据模型冲突、数据整合冲突[1]，严重地影响了后续的数据关联、数据挖掘、数据展现工作。时空数据冲突分析，作为探索具备时间维度和空间维度的属性值之间关联、约束和协调性问题的重要手段，在改善和提升地理信息、位置信息、商业信息、气象信息等数据资源质量与价值领域有广阔的应用前景，更是数据冲突研究的一个重要方向，但受限于研究方法、分析角度和关注程度，相关研究较为匮乏，目前研究主要集中在符合结构化、关系型或面向对象特征的一般性数据资源方向。

在数据结构冲突方面，张斌[2]较早探讨了面向对象数据结构中的对象标识冲突、模式冲突、语义冲突以及数据冲突，分析了数据不兼容和数据表示差异等问题。其后，唐新余[3]针对数据清理过程存在的数据冲突，提出一种基于简单一致性和概率分布的判别方法。刘万增[4]则综合考虑空间数据精度、目标类型、时态语义等因素，利用元数据结构、专家经验等形成了空间数据冲突的甄别方案。考虑到数据被水平或垂直划分时面临的冲突判别困难，仲志平[5]提出了一个分布式数据结构下的冲突检测算法，从而获得了违背条件函数依赖集的数据项。满靖[6]还研究了异构数据结构中数据交换的结构冲突和语义冲突。Wang[7]则以大规模数据中心为背景，使用博弈理论实施资源冲突的量化分析，有效地解决了同一数据集所引起的不同决策间的冲突问题。在数据模型冲突方面，被广泛探讨的是贝叶斯模型先验数据的冲突判别问题[8]，其逐渐被Al-Labadi[9]推广到鲁棒性和先验数据冲突之间的关系上，并在认识到共轭先验模型对先验数据冲突不敏感的基础上，由Walter[10]提出了一种基于威布尔分布的生存期模型，形成了先验数据冲突的分析方法。而针对分布式模型，从实践角度出发，封明玉[11]讨论了系统运行中数据冲突问题并提出了解决方案，Zhu[12]则依靠扩展关联和相似性理论，建立了扩展数据挖掘模型中的冲突分析和处理机制。在充分认识大信号处理模型的复杂性后，张德丰[13]、苏卫星[14]、宋巧红[15]则分别提出了基于小波变换的信号冲突判别算法，避免了传统检验统计量随着数据增多而无限增大的缺点。而在证据模型方面，Jiang[16]则基于修正的余弦相似度，提出了一种基本概率赋值（BPAs）方法来实现证据体间冲突程度的测度。另外，通过对多元数据间的一致性分析，李楚淮[17]还利用多边形间相似度、语义分类对比建立了多元数据模型中几何冲突和属性冲突的判别方法。在数据整合冲突方面，文静[18]研究了模式层次和语义层次上因数据细致程度、空间位置、结构差异等导致的数据冲突问题[19]。有鉴于不同冲突程度之间的相互影响，张永新[20]则提出了一种基于Markov逻辑网的两阶段数据冲突解决方法，Ichinokawa[21]更是建立了面向数据整合过程中的多数据集中的数据冲突分析方案。随着研究的深入，为了解决多数据源冲突[22]的主数据真值发现问题，王继奎[23]提出了一种非对称的数据值支持度计算算法，Khazalah[24]则提出了依靠反馈环节的冲突解决方法，并通过和解操作处理不同组之间的任何数据冲突。除此而外，Maunder[25]还在统计推断中实现了来自多个不同数据集的数据冲突的分析，为大规模数据集成数据质量提升奠定了基础。

综上所述，经过多年的研究，人们已经充分认识了数据冲突产生的根源和机理，基于概率分布模型、语义分析模型、变换域模型等开展了数据冲突判别，为来自不同数据源、结构迥异的数据冲突探索提供了解决方案。但仍存在一些不足：（1）现有研究重点是解决不同数据源、不同属性值、不同数据模型间的冲突问题，缺乏对具有多维特征的时空数据结构的探讨。（2）大多直接将时间维度、空间维度和属性值进行集成分析，忽略了空间位置、时间序列与属性值之间的冲突，仅有Jiang[26]和王巧燕[27]等少数学者分析了时空特征的数据资源冲突，探索了时空拓扑关系、实体属性变化等方面冲突问题。（3）依靠概率分布、先验模型的分析手段，通常假设时空数据符合某个特定分布，而抹杀了数据资源本身所具有的自然规律，降低了冲突分析的适用性和精度。为了进一步判别单个属性值与时空数据规律性之间的冲突，本文构建了一个基于Kriging方法和Pettitt检验的时空数据冲突判别方法：（1）将时空数据抽象为一个由时间、空间位置、观测值构成的元组，并通过紧致周边点集的构建为密切相关空间点位的确定提供解决方案；（2）给出周边点集Kriging转化方法，按照空间维度数据规律将属性值等效到判别点位上，为紧致周边点集属性值与判别点位属性值之间趋势规律的比较提供依据；（3）通过建立统计量来刻画Kriging转化获得的估计值与属性值间的差异，并借助Pettitt检验对差异曲线幅度突变的强识别能力，形成了一个时间维度和空间维度相融合的时空数据冲突判别方法，对时空数据是否违背时间、空间维度规律性进行了有效评判，支撑了时空数据质量与价值的提升。

2 时空数据特征与冲突分析

时空数据是处于时间维度和空间维度连续变化环境中所采集到的客观实体对象的属性值（观测值），它依赖于时空信息而存在，并常常呈现出动态的变化特征，具有明显的连续性和趋势性。这里的连续性体现为属性值沿着时间轴不间断的变化，且无论观测间隔何等微小总可以测得一个数据值。趋势性则是观测值受到内在机制和自然条件的影响，按地理位置呈现一种趋向性变化，因此时空数据的属性值通常不孤立存在，而沿着特定的时间演进过程或者地理空间路径存在一定的规律性。若定义l为位置、t为时间，则时空数据的属性值可以表示为Z(l,t)，也即是说t时刻在l位置测站所采集到的属性值为Z(l,t)，其中Z(l,t)依赖于时刻t呈现出连续性，而依赖于位置l呈现出趋势性。

目前，传统的时空数据冲突判别主要研究多个测站对应于同一个观测对象的情况，此时观测时间t一致，但可以获得l位置的多个属性值Zi(l,t)。如图1（a）所示，在t0时刻l1,l2,l3位置对l0位置实体对象的观测值Z1(l0,t0),Z2(l0,t0),Z3(l0,t0)之间存在冲突，此时冲突一方面来自Zi(l0,t0)之间数据结构，也可来自Zi(l0,t0)的计算模型。然而，对于另一类与历史信息和周边状况密切相关的时空数据来说（如气温、人口、降雨、水质等），受限于观测技术、仪器设备和实施环境，各测站只能观测其所在位置实体对象的属性值，因此上述冲突并不存在，但却引发了另外两种数据冲突，如图1（b）所示：（1）违背属性值的空间维度规律，Z(l0,t0)与同一时刻周边位置的属性值Z(lj,t0),lj∈Ω构成空间维度冲突，其中Ω为l0的周边位置；（2）违背属性值的时间维度规律，Z(l0,t0)与l0位置t0前后时刻的属性值Z(l0,tk),tk＜t⋃tk＞t构成的时间维度冲突，甚至与前后时刻l0周边位置的属性值Z(lj,tk)构成时空冲突，如气温数据脱离周边数据的陡然升高，或者相较前后时刻数据毫无迹象的突然降低。由于这两类冲突形成原因的特殊性，倘若仅仅依靠单个测站位置的观测值及其相似度分析来判别数据冲突实际上抹杀了空间维度，而将时空数据简化为空间数据进行探讨却又势必降低时间维度的信息量，因此需要一种能够融合判别点位l0周边信息以及判别时间t0的前后时刻信息的时空维度汇集方案，从而充分地利用时空数据资源形成数据冲突判别方法。

3 时空数据冲突判别

时空数据冲突判别是对来自不同时刻面状时空信息的一种数据分析工作，它要求以与判别点位密切相关的周边空间数据为背景，通过数据分析检测判别点位l0、判别时刻t0的属性值是否与周边位置及前后时刻数据存在冲突，亦即是否违反了时空数据时间维度和空间维度的规律性。为此，本文首先依靠空间位置关系确定出与判别点位l0密切相关的紧致周边点集，以避免仅仅依靠判别点位进行分析的片面性和将全体数据纳入判别过程而对算法精度的影响；然后借助Kriging方法将该点集上不同时刻的属性数据等效转化到判别点位上，实现空间维度和时间维度数据规律的汇集，摒除依靠相似度、语义分析时的无标度融合对时空信息和属性信息不同表征的忽视；最后利用t0前后时刻的数据以及等效转化后数据之间差异构造曲线，采用非参数检验方法，通过Pettitt突变检验在假定分布未知的情况下判断出判别点位l0、判别时刻t0的属性值是否存在冲突。

3.1 紧致周边点集确定

判别点位信息是时空数据冲突判别的关键依据，其周边点位的时空信息和属性信息也起着重要的支撑作用，然而传统方法对此类信息的忽视，导致冲突判别被简化为一个与空间分布规律、时间序列效应相无关的问题，从而时空数据的时空维度与属性值被割裂开来，降低了判别精度。为了能够把与判别点位紧密相关的空间点位信息纳入到判别分析过程，根据时空数据特征的分析，本文设n+1个测站的空间位置集合为L，li∈L,i=0,1,…,n为测站标号，并考虑到冲突检验对两端数据的迟钝性，定义时间窗口宽度为2wθ，时间跨度为判别时刻t0两端连续的2w+1个时间点tm,m=-w,-w+1,…,0,…,w-1,w分别表示时刻-wθ,-(w-1)θ,…,0,…,(w-1)θ,wθ，其中θ为数据采集的时间间隔，冲突判别则是给定(n+1)×(2w+1)个空间数据Z(li,tm),i=0,1,…,n,m=-w,-w+1,…,0,…,w-1,w，来判断t0时刻在判别点l0位置的属性值Z(l0,t0)是否与Z(li,tm),i≠0⋃m≠0存在冲突。此处要求i≠0⋃m≠0的目的是确保空间数据冲突的判别不仅仅依赖于l0位置的时间维度属性数据Z(l0,tm),m≠0并且依赖于周边位置的空间维度属性数据Z(li,tm),i≠0。但对于一个判别点l0来说，其周边测站或采集点众多，如果将其全部纳入到与判别信息相关的范畴，将使得部分无关数据被引入到评判中而降低精度，但如果仅仅依靠距离最近的若干采集点判断，则又丧失了数据分析的全面性，因此需要确定一个与判别点密切相关的紧致周边点集Θl0,Θl0⊂L。

图1 不同类型时空数据冲突

紧致周边点集由直接紧致周边点集和间接紧致周边点集构成。直接紧致周边点集记为Ωl0，它要求Ωl0内任意两采集点与判别点位所构成的三角形外接圆范围内不存在其他采集点（即每个采集点拥有强代表性），且在紧致周边点集中增加一个采集点，则必然使得原点集内中至少一个采集点不满足该相关性条件，该要求使得所选中的周边点集与判别点位密切关联并不可替代。紧致周边点集Ωl0的生成是一个类似局部TIN网形成过程，可参考文献[28]构建，或者如图2所示的简便方法：首先连接判别点位l0与各采集点，然后剔除共线但距离判别点位较远的点，最后以最短距离所构成的边按逆时针顺序寻找符合直接紧致要求的采集点，如果不满足则将其剔除重新寻找，找到后则以新采集点所构成的边为基础继续寻找直到所有采集点均被检索。对于间接紧致周边点集来说，则是考虑到Ωl0中任意一个采集点l∈Ωl0的直接紧致周边点集Ωl也与判别点位间接的紧密相关，由于Ωl中必然包括了l0，因此属于l的间接紧致周边点集可记为Ωl⋂{l′|l′∈L,l′≠l0}，进而将直接紧致周边点集和所有间接紧致周边点集合并起来即可构成l0的紧致周边点集Θl0：

3.2 紧致周边点集Kriging转化

紧致周边点集给出了判别冲突时可以使用的测站或采集点的位置，虽然这些测站的一系列属性值与判别点位的属性值有着密切的联系，但空间位置不同而规律不同，并不能代表判别点位的属性值，也无法直接根据这些数据做出是否存在冲突的判断，因此需要把这些空间维度数据规律聚集起来，如图3所示，按照一种转化方式将属性值等效到判别点位上，从而支持紧致周边点集属性值与判别点位属性值之间的趋势规律比较。该转化相当于探寻一个函数关系，使得其能在假定判别点位属性值未知的情况下由已知的紧致周边点集数据推求出一个判别点位的属性值，这恰恰等价于空间插值过程。插值时，由于在空间范围内连续性变化的时空数据属性值极其不规则，仅适合于用随机表面进行刻画，而Kriging方法作为地理空间领域所采用的核心统计方法，能够在考虑数据的空间变异性特征的同时融合数据的空间位置和相关程度，对时空数据的随机表面插值具有良好的适用性，因此本文采用Kriging方法并扩展至离散时间序列中，借助空间自协方差的最佳插值、探索性统计分析和变异函数建模，使得内插函数提供最佳线性无偏估计，依据协方差函数和回归算法对时空数据随机场进行空间估计，将紧致周边点集数据转化到判别点位，得到tm时刻l0位置Θl0点集转化值：

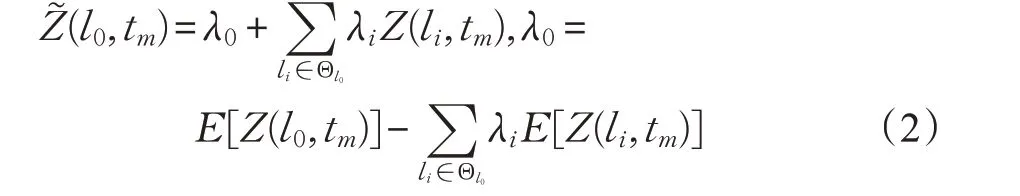
式（2）中λi为线性方程的系数。对来自不同空间位置li∈Θl0的属性值的线性组合正是对紧致周边点集空间维度规律的汇集，若令n=|Θl0|为Θl0中元素个数，根据无偏估计和方差最小条件可得到λi满足：

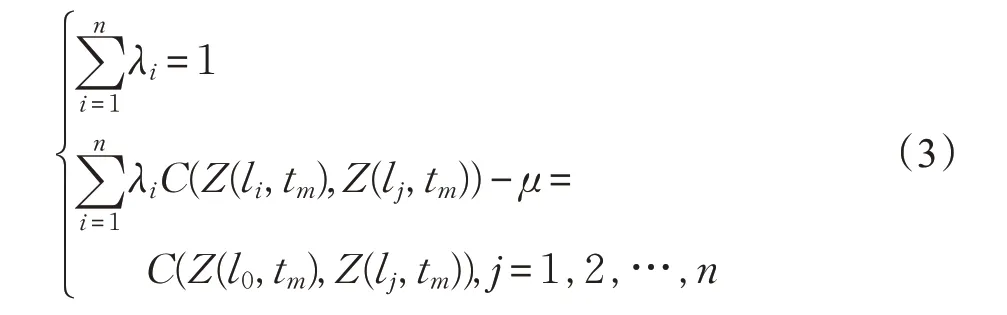
其中μ为拉格朗日乘数，C(Z(li,tm),Z(lj,tm))为Z(li,tm),Z(lj,tm)的协方差。为了获取λi的数值解，设l⊕h表示距离l为h的空间位置，N(h)为被h分割的空间点位的数据点个数，引入变异函数γ(h)及其估计量γ~(h)：

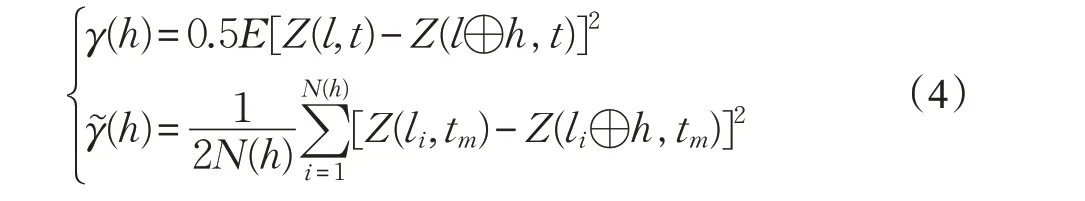
图2 直接紧致周边点集确定方法

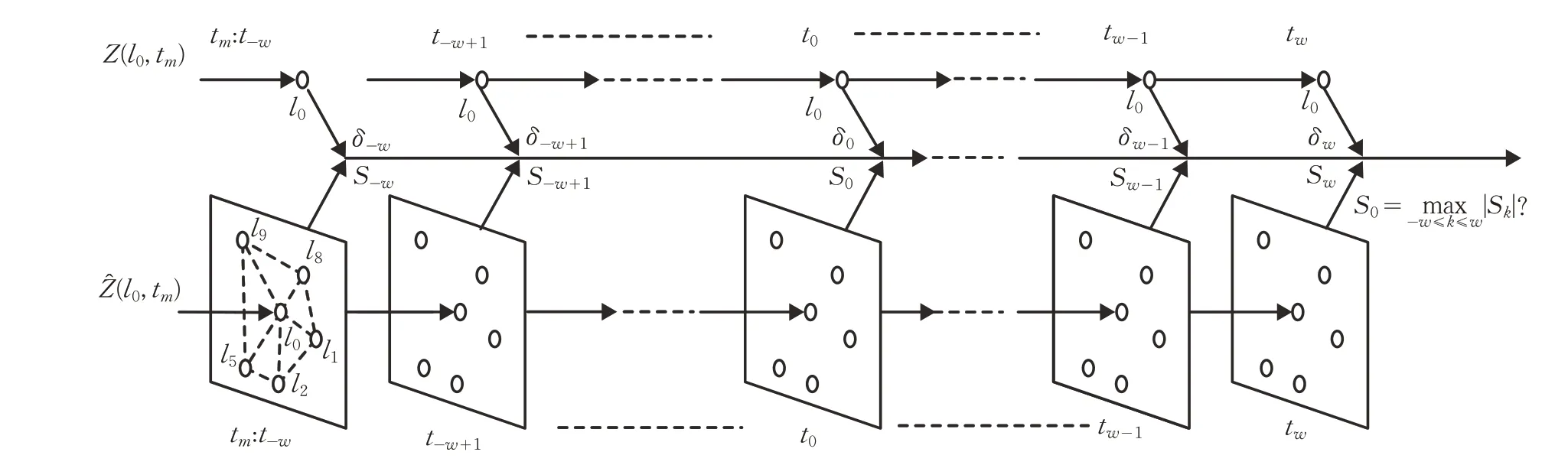
图3 时空数据冲突判别过程

基于式（4），考虑到在一个均匀的自然过程中，Z(l,t)与Z(l⊕h,t)之间的相关性常常依赖于它们之间位置，符合二阶平稳假设，其满足研究时段内区域化变量Z(l,t)期望等于常数(E[Z(l,t)]=m)，且区域化变量的空间协方差函数平稳（C[Z(l,t),Z(l⊕h,t)]=E[Z(l,t)Z(l⊕h,t)]-m2=C(h)），故而依据协方差函数与变异函数的关系C(h)=C(0)-γ(h)，则可以得到利用变异函数表示的Kriging方程组：

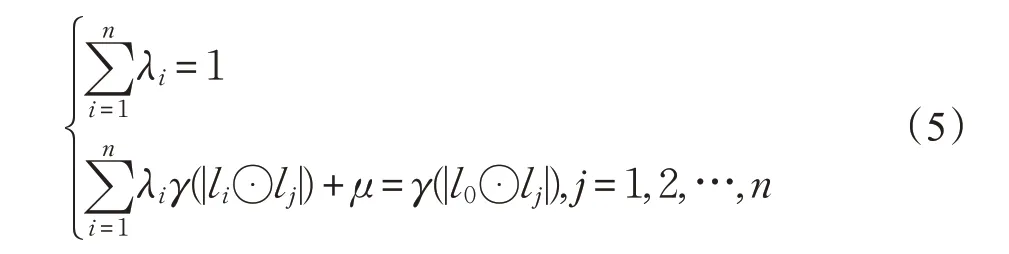
式中li⊙lj表示li与lj之间的空间距离。从中求解出λi并代入到式（2）中即可获得紧致周边点集转化值。满足Kriging方程组式（5）的转化值其期望为常数、方差最小，并体现了区域化变量的空间结构性变化和随机性变化，因此是最佳的线性无偏估计。

3.3 差异曲线突变检验

由于时空数据种类繁多且内在规律复杂多样，传统依靠参数检验的分析方法只能主观地假定时空数据服从某种概率分布然后加以判别，因而限定了时空数据的判别范围也为分析结论带了较大的不确定性。为了便于在分布未知的情况下采用非参数检验方法进行冲突数据的探索，强化时空数据规律在冲突分析中的重要地位，本文将冲突分析转化为差异曲线的突变检验，通过构造Pettitt统计量，以判别点位属性值与周边点集估计值的差异变化趋势来衡量数据违背时空规律性的程度。通过紧致周边点集的Kriging转化，将与判别点位密切相关的|Θl0|(2w+1)个属性值按照时间顺序依次转化到判别点位上，从而获得了按照空间维度汇集的2w+1个属性值Z~(l0,tm)，这些属性值可以看作是根据时空数据规律对tm时刻判别点位l0属性值Z(l0,tm)的估计，且在适度的时间窗口范围内Z~(l0,tm)与Z(l0,tm)沿着时间维度方向应具有相类似的连续性，之间差异变化的幅度不大，因此只需要检验这个差异值是否存在突变点，且如果突变正好发生在判别时刻t0，则说明Z(l0,t0)违背了时空数据的时间维度和空间维度的规律性，故而呈现为时空数据冲突。藉此，在给定时间窗口宽度2wθ下，抽取不同时间tm下的时空数据Z(l0,tm)以及通过Kriging转化获到的估计值Z~(l0,tm)，求其差值δm=|Z(l0,tm)-，如图3所示，按照时间顺序得到一个δm代表的属性值差异曲线，对该曲线判断其是否在t0时刻存在突变，如果存在则说明其统计特征发生急剧变化，故而Z(l0,t0)存在时空数据冲突。判断时，考虑到Pettitt方法是一种非参数检验方法，更适应于仅有单个突变点的检验，因此，对于样本容量为2w+1的时间序列δm,m=-w,-w+1,…,0,…,w-1,w，构建统计量Sk如式（6）所示：

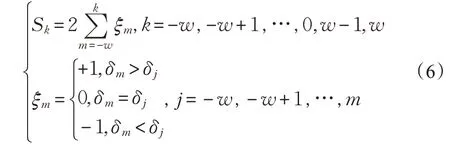
这里的秩序列Sk是第tm时刻大于或小于tj时刻数值个数的累计数。根据样本容量修改显著性条件为p=2exp(-/(w3+4w2+5w+1))≤0.5后，那么依照Pettitt方法，如果t0时刻对应的统计量S0符合该条件并满足则认为在t0时刻l0位置出现了时空数据冲突，且所判别出的冲突在统计意义上是显著的。

4 实验与分析

为了验证本文提出的时空数据冲突判别方法的有效性，使用陕西省宝鸡地区的降雨数据作为研究对象。地理空间信息来自1∶10 000的SHP矢量地图，涵盖29个重点测站，如图4（a）中图钉状图标所示，测站间最大距离155.6 km，最小距离8.7 km，每个测站在半径为40.0 km的范围内至少有2个临近测站。降雨数据中，时空位置对应于测站所在经纬度位置，采集时间间隔则为θ=2h，如表1所示，共计从2012年1月1日至2016年12月31日提取降雨量时空数据635 796个。

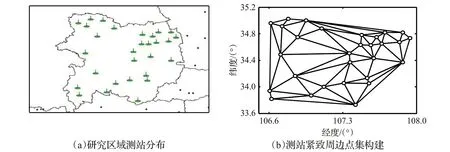
图4 研究区域测站分布及紧致周边点集

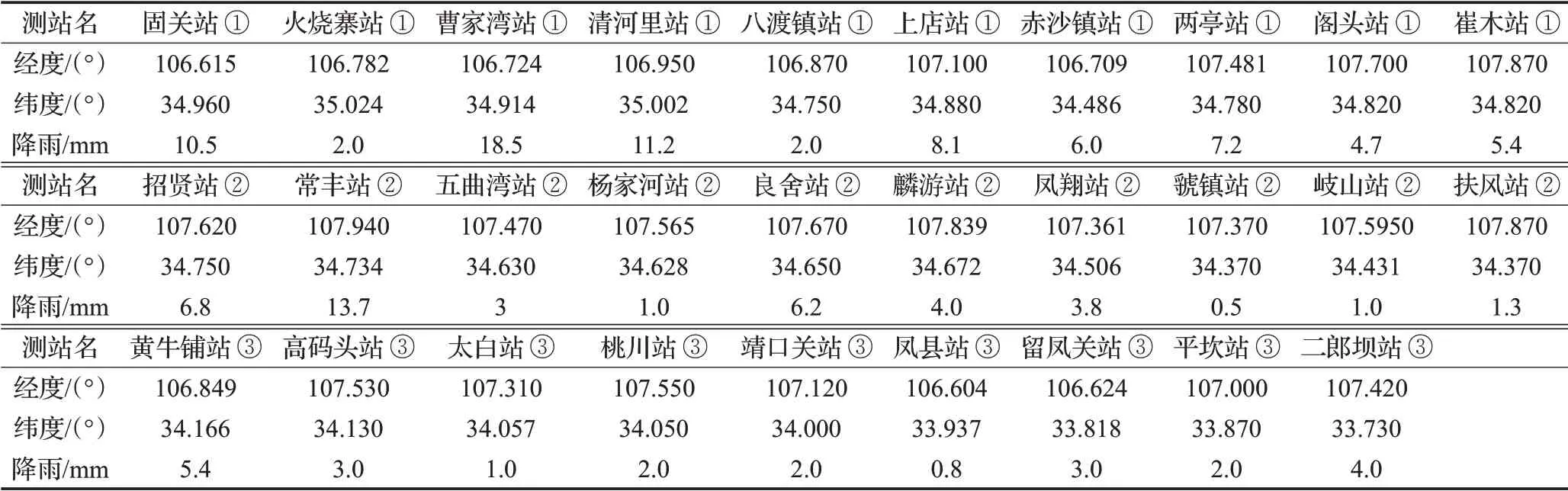
表1 测站空间位置及部分降雨数据

为了便于数据分析，对于降雨数据缺失的时刻使用“0”值进行填补，同时考虑季节变化以及地势形态对降雨状况的影响，时空数据冲突判别重点判断由于计量仪器设备故障所导致降雨数据明显违背自然降水规律，而与周边以及历史数据不协调的冲突。在进行网状图生成后，进行临近周边点集分析，逐步建立29个测站的紧致周边点集，如图4（b）所示，各测站的直接紧致周边点均大于3个、间接紧致周边点均不少于5个，而部分测站的紧致周边点总数则高达20个，为冲突判别提供了充分的周边时空数据资源。考虑到强降雨一般持续不超过2天，故选取时间窗口宽度为48 h(w=24)，共计2w+1=49个时间点开展实验如下：

（1）以岐山站为判别点位，按照直接紧致周边探索方法，从正东方向开始依次获得良舍站、杨家河站、五曲湾站、凤翔站、虢镇站、高码头站、扶风站等7个直接临近站，其距离岐山站在[21.6，34.1]km范围内。进而得到间接紧致周边点集由麟游站等13个测站构成，处于岐山站[35.5，81.4]km范围内，总计紧致周边点n=20个。限于篇幅，对于从0时至6时的连续四个时刻，使用式（5）计算得到用于周边点集转化的线性组合参数λi,i=1,2,…,20，分别如表2所示，将各参数应用到式（2）逐个把紧致周边点集的降雨数据使用Kriging方法转化到岐山站，为了清晰地表示数据结果及其与周边数据情况，此处综合其他各测站位置降雨数据，在经度[106.5，108.0]、纬度[33.6，35.2]研究区域内，构造一个175×140像素的图像，将各时刻降雨信息按地理位置映射到该二维图像中，如图5所示，可见存在一个降雨中心。单独抽取岐山站的时间序列计算差值δm，并绘制δm与采用Pettitt方法构造出的秩序列Sk曲线，如图6所示，可以看出在判别时刻t0秩序列曲线恰为最大值，计算得p=0.47＜0.5，这表明此时岐山站降雨数据存在冲突，分析其实际原因发现岐山站周边28 km范围内杨家河站等测站普遍降雨，超过了20.0 mm，形成降雨中心，而其他位置则为0 mm，违背了降雨分布自然规律，产生冲突，这是由于强降雨引起自然灾害导致数据传输丢失。另外，考虑到紧致周边点集Kriging转化实际上是根据周边情况估计出判别点位的属性值，因此可以使用转化值来替换判别点位的属性值，以消除时空数据冲突。

表2 线性组合系数演算结果

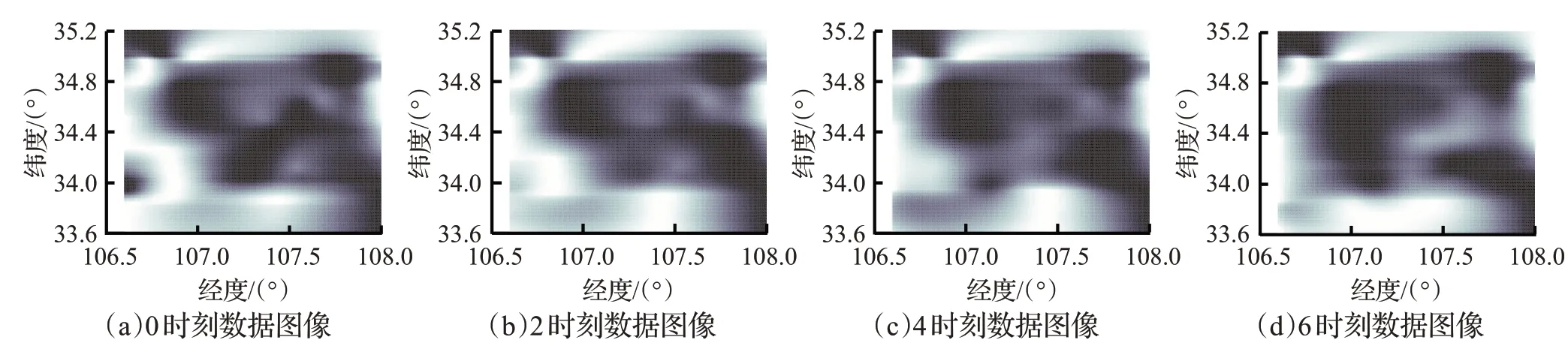
图5 不同时刻空间数据图像

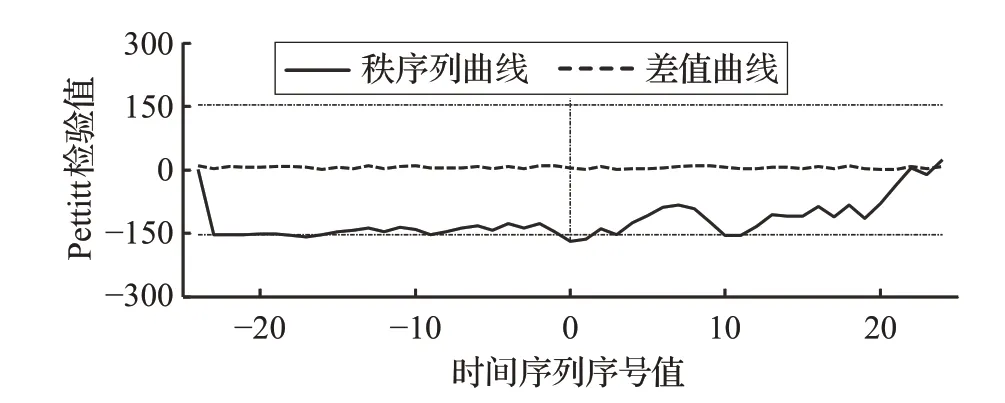
图6 时空数据冲突判别差值曲线及秩序列曲线

（2）考虑到数据冲突均是偶尔发生，因此为了通过批量数据验证方法的合理性，以时间窗宽度48 h为间隔将降雨数据库进行修改，形成一个人工样本。如表3所示，将第①组测站中数据中随机的50个降雨数据修改为0，假定其为数据丢失，而将第②组测站中非零值的50个降雨数据修改为原值的1/3，将第③组测站中50个降雨数据修改为原值的3倍。针对这150个时空数据判断是否存在冲突。从第①组中判别得到31个数据冲突，正确率为70%，而未被判别出的时空数据冲突为19个，其主要是因周边测站及前后时刻均只有零星降雨且不超过3 mm，因此0值被认定为无降雨，符合降雨分布规律，故而造成误判。从第②和③组中正确判断出85个冲突数据，正确率分别为88%和82%，有良好的冲突判别能力，但仍有15处误判。分析这误判点位发现其均发生在降雨范围小、短期强降雨情况下，此时降雨过程短促，在不到采集间隔θ=2小时内降雨从峰值降低到20%以下，且又由于周边测站相距较远而不能准确获取小范围雨量信息，因此将降雨起始时刻急剧增长的属性值或降雨结束时刻急剧下降的属性值修改为普通值，并不能从周边测站或前后时刻信息中所感知，此时降低至1/3或提升3倍被看作符合降雨量变化规律，从而导致误判。显然，在这种情况下，增加测站的分布密度、缩短采集时间则能够有效应对短期、小范围数据变化，从而提升时空数据冲突判别的正确率。

表3 不同时空数据样本冲突判别正确率

（3）为了与传统方法比较，选取参数检验方法和相似度方法开展对比分析，其中参数检验方法假定日降雨数据服从正态分布，以时间窗宽度48 h内24个数据作为样本采用拉依达准则作为数据冲突判别条件；相似度方法将空间维度和属性值分别使用Min-Max方法进行归一化，然后进行无权值汇集，在时间维度利用向量夹角余弦分析当前数据与历史数据的相似度，时间窗宽度仍取48 h，以引入判别点位数据使相似度降低超过阈值0.1作为判别冲突的条件。经过对3组数据判别可以发现：因干旱或强降雨数据影响，参数检验方法对赋“0”数据和超大数据冲突仅具有一定的识别能力，而对于离均值相对较近的冲突判别则精度极低；而相似度方法因采用了与分布无关的数据向量分析，几乎不受冲突样本的影响，但这种时空融合方案损失了时空维度信息，判别率均未超过70%；本文方法由于在判别过程中综合了周边数据以及时空规律因而获得更高的检验精度，相对传统方法在不同冲突样本下精度分别提升6%、22%、20%，进一步提升了冲突判别的实用性。

5 总结

数据冲突的识别与处置一直以来是提升信息资源质量的重要环节，并随着大数据技术的不断发展，逐渐成为了众多学者研究的热点。为了实现地理位置分散固定的时空数据采集系统中数据冲突的判别，本文在分析时空数据冲突特征的基础上，构建了一个以属性值为核心并融合时间维度和空间维度信息的时空数据判别方法，该方法通过确定紧致周边点集来获取与判别点位密切相关的测站分布，并经过Kriging方法开展周边位置、前后时刻的属性值的转化，继而通过Pettitt检验对差异值跳跃性转变的识别，为时空数据冲突的判别提供了一个解决方案，并经过实验验证了方法的有效性和实用性，不同冲突样本下可分别获得70%、88%、82%的判别正确率。考虑到紧致周边点集建立时以构建三角外接圆为条件，这势必在边界处将距判别点甚远的测站纳入到点集中（如边界处崔木站与其直接紧致周边清河里站相距竟达86.2 km），影响了时空数据判别精度，因此下一步的工作主要是尝试不同要求下紧致周边点集的建立方法，并综合时空数据的趋势性构建与判别点位更为密切的紧致周边点集，进一步提升时空数据判别能力。