基于地理空间大数据的高效索引与检索算法
2020-02-19赵慧慧陈仁海冯志勇
赵慧慧 赵 凡 陈仁海 冯志勇
1(天津大学智能与计算学部 天津 300350)2(天津大学深圳研究院 广东深圳 518000)3(天津大学国际工程师学院 天津 300350)
近年来,国家城市化进程不断加快,2维地理空间信息数据更新迅速,其中道路网络数据不仅是路径规划、城市建设、位置服务及智能交通的基石,更为数字城市、智慧城市的发展奠定了基础[1].在城市信息化浪潮与数据科学崛起的共同推动下,智慧城市的发展不仅需要庞大的地理空间数据作为载体,更加需要高效的空间检索技术推动智慧城市的发展[2].地理空间大数据作为大数据的一个分支,正在全球范围内迅速崛起[3],空间大数据的时代已经来临.
空间大数据无疑将重构很多行业的商业思维和商业模式,其价值不言而喻[4].与此同时,随着定位技术的发展,空间大数据的位置标签越发精确.例如,有了WiFi、卫星定位、移动通信蜂窝定位技术及其变速器、微陀螺、速度传感器等多种多样的微小传感器的支持,才使得虚拟社交网络系统(social network system, SNS)发展到真实世界与虚拟世界相融合的基于位置的社交网络(location based social network, LBSN),并成为互联网企业的必争之地.在人工智能领域,无人驾驶作为其行业最受关注的应用之一,在其应用中道路网络数据是其必不可少的实现基础.例如,高精地图需要个性化驾驶支持,包括各种驾驶行为建议,如最佳加速点及刹车点、最佳过弯速度等,以提高无人驾驶的舒适度[5].并且无人驾驶汽车可以通过本地计算来实时地对当前路况做出反应,而不用连接到高延迟的远程控制中心[6].在智能交通系统领域,信息采集设备的普及,每天都会采集海量的2维地理空间信息数据,这些数据极为宝贵[7].例如,通过对某个时间段某个路口采集到的车辆情况对该路口的车流量进行分析,可以获悉该路口的路况,向司机及时提醒道路的拥堵状况等.在遥感领域,地理信息系统和定位导航等技术逐渐商业化公众化之后,遥感数据观测与服务也正在从政府主导的公益应用向公众与商业机构主导的商业与公众应用扩展[8].在日常生活中,人类所产生的数据有80%和空间位置有关[9],具有互动、非专业、实时、泛在、按需服务、SOA特征的新地理信息时代[10]必将是空间大数据(big geo-data)备受瞩目的时代.
大数据时代科学研究是一个大科学、大需求、大数据、大计算、大发现的过程[11].而空间大数据是在城市基础地理信息基础上,将各个曾经孤立的、服务内容单一的,但具有城市管理功能的空间信息、动态信息和公共信息等城市及信息聚合而成面向大众的、跨领域的、跨系统的社会化服务信息[12].空间大数据作为大数据与地理信息数据的融合体,在信息时代扮演着重要的角色,已经逐渐发展成为当今社会最基本的信息服务之一.然而,面对海量的数据检索时,单单依靠传统的空间索引技术,频繁的插入和删除操作会增大2维地理空间信息数据地重叠率,数据存储中存在许多彼此相似的数据块[13],从而导致查找路径不唯一的情况增多,查询效率变低.
如何在分布式存储的模式下设计空间索引、提高检索效率,是空间索引技术未来重要的发展方向.本文以空间索引技术为主线,总结空间大数据下空间索引技术的背景、研究现状,分析不同索引类型的优劣;重点讨论每个时期空间索引技术的变化与技术创新;然后提出多层切片递归空间索引算法(multi-layer slice recursive, MSR),并与当前主流的空间索引技术基于R树的批量加载算法(sort tile recursive, STR)、STR-网格混合算法(str-grid)及高效几何范围查询算法(efficient geometric range query, EGRQ)进行实验对比.实验结果表明,MSR算法不仅减少了道路网络空间数据的重叠度,提高了检索效率,而且可以很好地利用内存空间,减少存储空间的浪费.最后结合其面临的机遇与挑战,对2维地理空间信息数据做出展望.本文提供了实验数据以及实验代码的GitHub链接[14],以供其他研究人员研究.
1 相关工作
2维地理空间信息数据是地理空间信息的重要组成部分.2维地理空间信息数据除了具有一般大数据体量(volume)大、类型多样(variety)、处理速度(velocity)快、价值密度(value)低、真实性(veracity)高等特点外[15],还具有其自身鲜明的特点,主要体现在:1)全样本持续更新,数据呈现的是全样本的、客观的、过程的以及连续性的数据类型特点,数据资源更加全面、丰富、时效性更强;2)多维度,道路网络数据不仅局限于点、线、面,向着更高维空间发展;3)多粒度多层次,道路网络数据中碎片化、零散化、低效率的数据查询和分析普遍存在.面对如此规模庞大并且复杂的2维地理空间信息数据,传统的空间索引技术无法满足大规模数据快速检索和查询等需求,此时,需要查询效率高效的空间索引技术.
空间索引结构是一种辅助性数据结构,它基于空间数据的位置、形状以及对象之间的空间关系来组织空间数据结构,目的是提高数据检索及其他空间操作的效率.传统的空间索引技术主要分为三大类,分别为基于网格的空间索引、基于树结构的空间索引、混合空间索引.
1) 基于网格的空间索引.基于网格的空间索引技术通过横竖线条把空间区域划分为若干个大小相同的网格,每个网格中包含空间对象,当用户查询时,首先检索出用户查询的空间对象所在网格,再从网格中定位到目标空间对象的位置.网格空间索引的方式很简单,当数据分布均匀时,其空间查询效率很高.但是网格的大小会影响到索引表的大小,如果网格太小,索引就会膨胀,不但查询效率低,而且对索引表的维护费用也会增加.目前有很多学者对此做出的分析和研究,提出了不同的解决方案.分别为基于规则网格划分的空间索引、基于多级空间网格划分的空间索引、自适应层级网格化分空间索引.
2) 基于树结构的空间索引.在基于树结构的空间索引技术中,具有代表性的树结构分别是R树与四叉树空间索引.国内典型的地理信息软件如MapGIS与SuperMap,其空间索引技术采用的是四叉树索引;国外比较著名的地理信息软件如MapInfo公司的MapInfo,其空间索引技术采用的是R树索引;以及国外Oracle公司的Oracle_Spatial组件采用四叉树与R树混合的空间索引技术.
R树是一种高度平衡树,它是在B树基础上扩展了多维空间.R树索引技术的本质是面向对象的分割索引技术,分割后的区域与每个结点相对应,每个结点又与1个磁盘页对应,尽管磁盘存储系统有效地提升了带宽,但访问延迟难以得到有效解决[16].R树不但能控制树的深度,而且还能采用最小外包矩形[17]表示空间实体,是最早支持多维空间存取的方法之一.该算法提高了空间数据检索和空间操作的效率.
四叉树是另一种常见的树状索引结构,可分为点四叉树和区域四叉树,适用于点数据、区域数据以及高维空间数据的索引结构建立.在四叉树结构中,空间要素标识都记录在外包络矩形覆盖的每个叶结点中,所以在内存中的层次树状结构的查询效率较高.
3) 混合结构空间索引.混合索引结构汲取了各个索引结构的长处,多种空间索引的融合也是空间索引技术发展的方向,其大致可以分为3类:基于网格与树结构的混合索引、基于多个树结构的混合索引以及图与树结构的混合索引.
网格与树混合索引的典型是基于固定网格与四叉树结合的空间索引机制.这种混合索引机制通过使用索引结点表和Hash技术管理类对象结点表,达到节省存储空间的目的,因此有效地减少了磁盘读取次数,显著提高了空间查询速度.空间对象与叶子结点出现了多对多的情况,但是相比之下,基于固定网格与四叉树结合的空间索引机制,能够使大面积空间对象重复减少;其不足之处在于算法的空间复杂度比较高,维护比较困难.
多个树结构的混合索引有很多,具代表性的是QR树,首先利用四叉树将数据库的研究区域分割为多级子索引空间,然后将R树索引应用到各级中的每个子空间.这种混合索引机制的优点是利用缩小的空间范围提高了查询效率,数据量越大索引效果越好.但是该方法没有考虑到大空间对象对数据的影响,在检索大范围空间对象时,其检索效率往往不高;索引占用的空间也比R树大.
图与树的混合索引机制,一般将图论的思想应用在空间索引范畴上.基于MR-Tree空间索引的Voronoi图改进及其并行空间查询方法,在MR-Tree索引基础上,引进了邻近关系判断,以替代范围查询中的冗余计算,有效地提高了分布式环境下的空间操作的效率.
国外研究空间索引的成果最早可追溯到20世纪70年代文献[18]提出的四叉树索引,这是一种树状数据结构,在每个结点上会有4个子区块,将数据空间均匀的划分为4个象限,数据范围可以是矩形或其他任意形状.文献[19]提出了KD树(多维二叉搜索树),KD树是每个点都为K维点的二叉树,其在点的查找上有着与二叉树一样良好的性能.文献[20]提出了KD树的改进——非同构KD树,降低了删除的代价.文献[21]介绍了R树这种处理高维空间存储问题的数据结构.文献[22]提出了网格的思想,通过网格划分数据空间,再利用网格地址检索相应磁盘页.这一方法主要用于多维点,对于其他目标并不适用.文献[17]提出了最佳动态R树的变种——R*树,R*树和R树一样允许矩形的重叠,但在构造算法上R*树不仅考虑了索引空间的“面积”,而且还考虑了索引空间的重叠.文献[23]利用Hilbert分形曲线,对N维空间数据进行1维排序,进而对树结点进行排序,为获得较高的存储利用率对排序后得到的结点集实施滞后分裂算法,这也形成了Hilbert R树算法的核心.文献[24]提出了R树的变形树STR树.文献[25]提出了一种连续K最近邻查询算法,将当前参考点进行迭代操作,使当前参考点移动到最近的分割点.
国内研究的空间索引技术起步于20世纪90年代,文献[26]提出一种G树的空间模型和动态网格的操作算法.借鉴Windows NT等操作系统采用页面来管理虚拟内存的方式,设计实现了基于页面的新的空间索引机制,有效地解决了N维空间数据的索引问题.但其结点的空间利用率相比其他索引树而言偏低.文献[27]提出了基于Hilbert空间排列的点特征二叉平衡排序树动态索引结构和基于角点回溯的线特征索引结构,为动态内存索引与磁盘索引提供了新的思路,并满足GIS数据模型的要求.文献[28]针对现有R树索引不支持空间数据多尺度表达的问题,提出了一种用于空间数据多尺度表达的树变形索引结构,该算法在检索多分辨率形式组织的空间数据时效果显著.文献[29]提出了基于线性四叉树结构的Voronoi图反向膨胀生成算法.文献[30]提出了基于MR-Tree空间索引的Voronoi图改进及其并行空间查询方法.
以上描述的空间索引技术及其变体,是针对不同应用、不同类型及不同需求的空间数据对象,在某些领域有其自身的优势,但换另一种数据结构也许在查询效率上就稍逊一筹了.
本文提出的MSR算法首先对地图数据划分切片,然后在单一切片内聚类对比,在相邻切片内进行聚类以此保证数据间拥有最大程度的空间邻接性;其次,按照一定范围构建叶子结点类并处理离散值;最后自下而上递归生成MSR树.MSR算法能够很好地处理数据密度高畸变的空间区域并且不会出现磁盘浪费的情况.这是因为MSR算法减少了矩形框的重叠率,查找路径不唯一的情况很大程度减少,所以其查询效率较高.通过与当前主流的空间索引技术STR算法、STR-网格混合算法(STR_GRID) 及EGRQ算法进行实验对比,验证了本文提出的算法的良好性能.
2 MSR算法相关知识
在本节中,首先介绍基于2维地理空间信息数据的空间索引机制在构建过程中涉及的概念,然后介绍一种基于R树的批量加载算法——STR算法、一种混合空间索引机制STR-网格算法及EGRQ算法.
2.1 基本定义
基于地图数据的空间索引机制主要是针对优化道路网络数据查询而建立的空间索引结构,其中2维空间道路网络数据查询主要包括2个方式:点查询和区域查询.点查询就是在索引结构中找到距离目标点最近的空间对象,而区域查询是找到给定区域中的所有空间对象,所以区域查询更加复杂.
定义1.空间数据.空间数据是用来表示空间对象的位置、大小、形状及其分布特征诸多方面信息的数据.它可以是点、线、面以及高维的多面体等,比如地图上常见的建筑物、道路、城市.
定义2.最小外包矩形[31].最小外包矩形(mini-mum bounding rectangle, MBR)是指以2维坐标表示的若干2维形状(例如点、直线、多边形)的最大范围,即以给定的2维形状各顶点中的最大横坐标、最小横坐标、最大纵坐标、最小纵坐标定下边界的矩形.最小外包矩形是最小外接框(minimum bounding box, MBB)的2维形式.
定义3.R树[32].R树是用来做空间数据存储的树状结构.例如给地理位置、矩形和多边形这类多维数据创建索引.
其核心思想是聚合距离相近的结点并在树结构的上一层将其表示为这些结点的最小外包矩形,这个最小外包矩形就成为上一层的一个结点.叶子结点上的每个矩形都代表一个对象[33],结点都是对象的聚合,并且越往上层聚合的对象就越多.也可以把每一层看作是对数据集的近似,叶子结点层是最细粒度的近似,与数据集相似度100%,越往上层越粗糙.
定义4.聚类[34].聚类是将数据集中的数据根据各自的特征分成不同的簇,簇间尽可能相异,簇内尽可能相似.
聚类是数据挖掘中的一种无先验条件的无监督分析方法.早期传统的聚类查询算法主要关注于获得精确的聚集统计值[35].
2.2 STR算法的构建过程
STR算法主要是应用于区域查询而构建的树型索引结构算法,它基于排序思想构建的R树可以达到近乎100%的空间利用率.STR算法中假设2维空间有N个对象的最小外包矩形(MBR),每个R树结点的最大容量为M,STR算法的基本思想为:按MBR中心点的X坐标对其排序,等分为S组,并使每一组中包含M×S个空间对象,在每一组中用MBR中心点的y坐标进行排序,每M个MBR形成1个新的结点,并将新结点的MBR作为下一次递归的输入,自下而上生成整棵R树.
2.3 STR-网格混合算法
STR-网格混合算法首先通过对空间区域进行划分,缩小研究范围,达到提高检索效率的目的.基本思想是通过横竖线条把空间区域划分为若干个相同大小的网格,每个网格代表1个存储桶,将落在该网格中的空间对象放入对应的存储桶中.之后根据桶中的空间对象的多少,继续划分网格,直至每个子网格中的空间对象个数满足阈值,最后对每个子网格中的空间对象按照STR算法再进行组织索引.当用户进行查询操作时,首先检索出用户查询的空间对象所在网格,然后再通过STR算法从网格中定位到所需空间对象的位置.
2.4 EGRQ算法
高效几何范围查询算法EGRQ,采用安全KNN计算、多项式拟合技术以及R树索引,来提高空间对象的查询效率.
STR算法、STR-网格混合算法和EGRQ算法都有其固定的缺陷.STR算法不能很好地处理数据高畸变的空间区域,其查询性能低效.STR-网格混合算法首先通过网格对空间区域进行划分,然后再在每个网格中构造STR树.当网格对空间区域进行划分时,将空间区域划分为多个子空间,这种划分方式全凭经验.如果对空间区域划分时出现网格划分过细的情况,则会导致耗费磁盘存储空间和搜索时间过长,磁盘存储冗余大,造成磁盘浪费,内存利用率低;如果网格划分过大,则该方法不能很好地处理数据密度高畸变的空间区域,导致其查询效率降低.本文提出的MSR算法能够很好地处理以上问题.
3 MSR算法的设计与实现
在对2维地理空间信息数据研究过程中发现,随着空间对象的增多,空间对象的MBR之间的重叠现象会不断加大.目前针对2维空间对象(点、线、面)的查找方式多以相交、距离等判定方法,这种方法导致空间对象之间的MBR重叠数量加大,使查询过程中无用路径的数量变多,从而影响查询效率.本文提出的MSR算法从优化空间对象之间的MBR重叠数量这一角度出发,根据空间邻接性法则交叉搜索相邻切片中的空间对象,同时使用空间聚类方法修正单维度排序所造成位置分布过于稀疏的问题,以自下而上的方式生成空间索引树型结构.
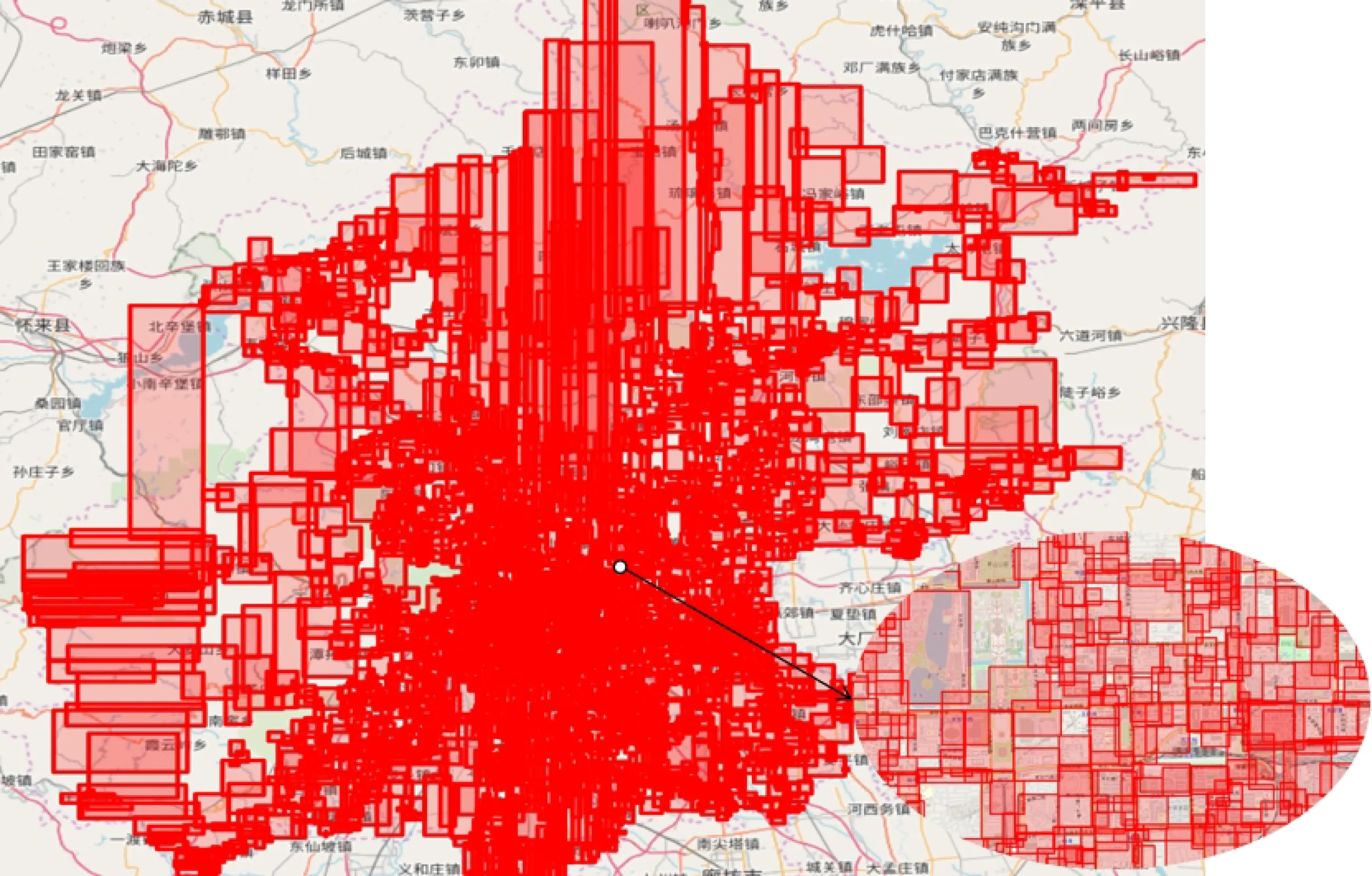
本文采用的空间对象是全国道路网络数据,图1是北京市道路网络数据的MBR的效果展示图.可以看出,空间区域中MBR重叠现象严重.如果在数据量庞大的、复杂的、形状多种多样的全国道路网络数据中查询目标数据,合理、高效的空间存储索引结构是简化检索路径、缩短检索时间最有效的方法.
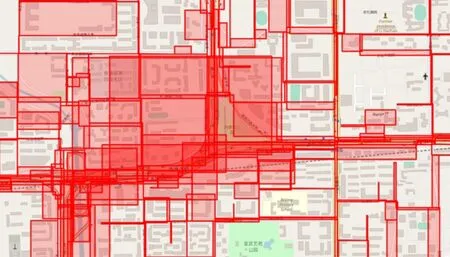
Fig. 1 Road network MBR renderings图1 道路网络MBR效果图
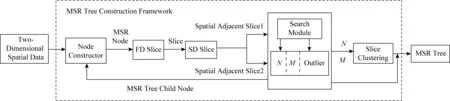
Fig. 2 MSR algorithm framework图2 MSR算法框架
3.1 MSR算法概述
MSR结构一共包含3种结点:根结点、子结点和叶子结点.根结点和子结点主要存储孩子结点的位置,叶子结点主要存储空间经纬度信息.MSR算法构造的空间索引树框架图如图2所示,其中2维地理空间数据在第1维度排序且切分后形成的数据集表示为FD(first division)切片,SD(second division)切片表示2维地理空间数据在第2维度排序后形成的数据集.经过FD切片和SD切片操作形成数据集.至此,MSR构建完成.
下面介绍MSR算法的整体流程:
输入:2维地理空间信息数据中的r个空间对象,每个结点的最大容量为N;
输出:包含r个空间对象的MSR空间索引树.
1) 计算所有2维地理空间信息数据的MBR,对树结点的各项信息做初始化操作;

3) 对每个切片中空间对象按照第2维度进行排序;
4) 按照排序后的结果寻找一个未聚类的对象作为初始化类C;
5) 考虑到空间对象的邻接性和空间对象的分布情况,根据初始类的MBR中心点位置向四周一定的范围内设定搜索框S;
6) 计算搜索框S包含的当前切片和相邻切片中所有的空间对象,得出命中对象列表H,其长度为L;
7) 如果命中个数L≥N-1,在命中列表中寻找距离类中心最近的空间对象,将结果归到类中,更新类大小和类中心,知道满足结点容量;
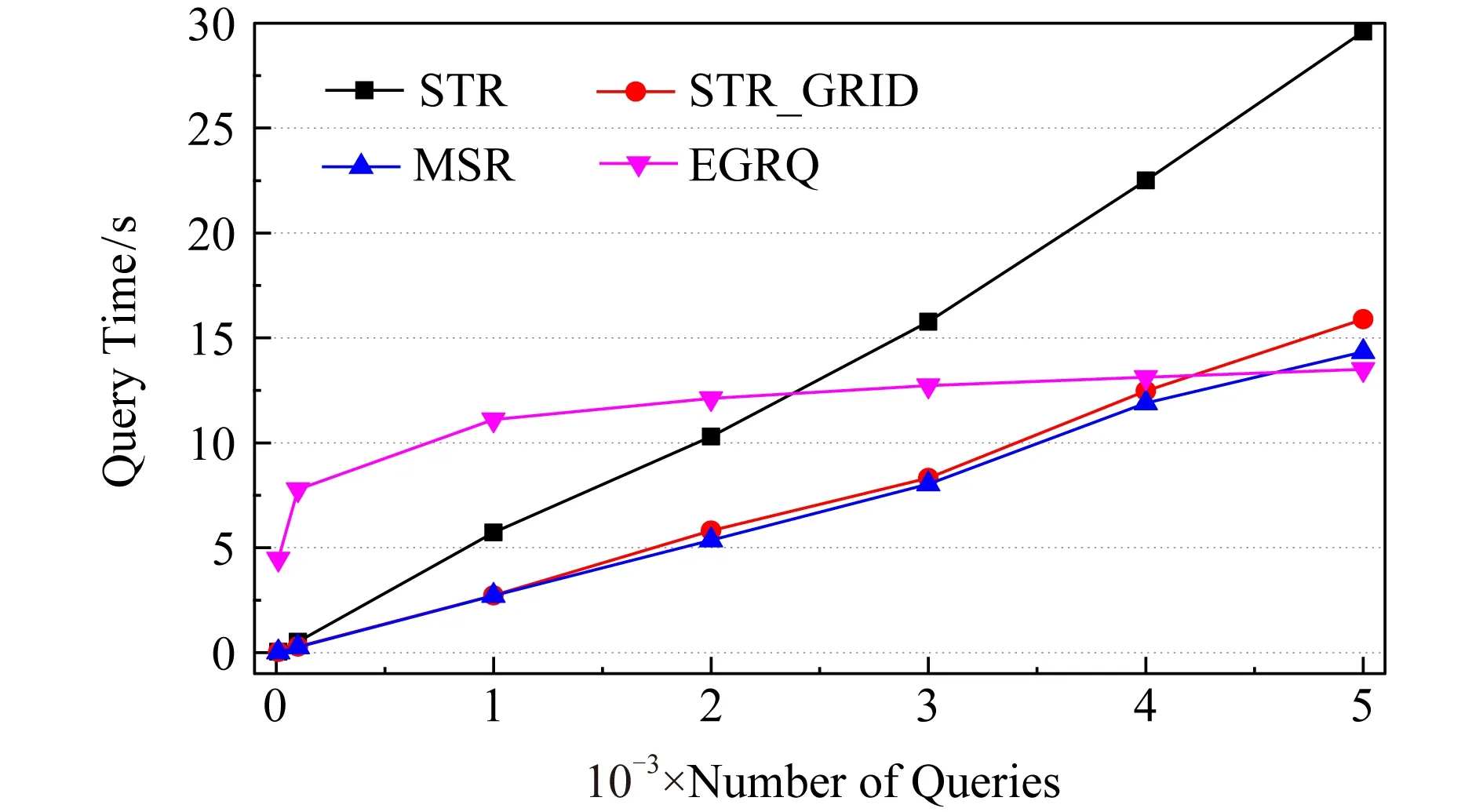
8) 如果命中个数L 9) 按照步骤4)~8),每2个切片为1组,遍历全部切片,最后1个切片也按照上述原则构造; 10) 按照步骤1)~9),自下至上,递归构建,最终生成根结点.至此,整棵MSR树构造完成. 图3展示了MSR树的生成过程实例,对空间区域中编号为1~10的空间对象求出其MBR.然后进行第1维数据排序和切分操作,其结果为:1,4,2,6,7,5和8,9,3,10,再对每个切片进行第2维排序操作,其结果为:1,2,5,4,7,6和3,9,8,10.最后按照MSR算法取2个切片中的数据聚类为矩形框11,12,13,14和15,16,这样第1层叶子结点就生成了,接下来就是不断地执行递归操作,直到生成根结点. Fig. 3 MSR tree generation process图3 MSR树生成过程 在本节中,我们给出MSR构造算法生成的伪代码,MSR构造算法的算法描述如下所示: 算法1.多层切片递归算法. 输入:当前切片Tilec和相邻切片Tilea,搜索框B; 输出:MSR空间索引树; 过程:MSR(Tilec,Tilea,B)→MSR空间索引树. ①GET_search_List(Tilec,Tilea,B)→Hlist; ② Letcluster←C;*将当前切片的首个未聚类的数据初始化为新的类* ③ ifHlist.length≥N-1*根据命中数据的大小分别处理* GET_clustering(Hlist,C); else ifN2-1≤Hlist.length≤N-1 Cluster←Hlist; elseOutlierlistappendHlist; ④ End if ⑤MSRinsert(Nodelist,Outlierlist)→Nodelist; ⑥TreeNodeConstructor(Nodelist)→Nodelist; ⑦ ifNodelist.length>1*执行递归操作,直到生成根结点* LetTilec←Tilea; LetTilea←Tilea.next; MSR(Tilec,Tilea,B)→MSRTree; ⑧ End if ⑨ Output(Nodelist).*输出整棵树* 在MSR构造算法中,搜索框是以类的矩形框向四周以一定距离为半径进行搜索的空间范围,同时每次聚类操作结束后都要把已完成聚类的空间对象进行标记,以免重复利用.在聚类过程内部,要注意每次添加数据后需要实时更新类的大小和中心点,对于命中空间对象个数的使用规则是参考了R树结点容量的性质,即每个结点包含[m,N]个数据,其中一般m=N2. MSR树的查找和STR类似,自下而上逐渐将下层的数据矩形抽象到高层的正方形,即对下层数据矩形有正方形化的趋势.检索算法从树的根结点开始,它将所有与查询区域存在交叠的结点的子结点查出,然后将这些子结点作为当前结点检查它们与查询区域是否存在交叠,直到找到叶子结点的空间对象.MSR算法通过判断MBR与查询窗口是否相交,如果相交则遍历所有孩子结点继续判断,直至获取到叶子结点的空间对象信息. MSR树的更新和R树类似,对于搜索路径上的每个结点,遍历其中的最小外包矩形(MBR),如果搜索到1个叶子结点,则比较搜索框与它的最小外包矩形和数据,如果该叶子结点在搜索框中,则把叶子结点加入搜索结果.添加操作如果遇到结点溢出则分裂,分裂的方法和R树相同,都是更新相关的一条路径上的信息,并且为了尽可能少出现结点溢出的现象,在进行实验时,会为每个结点设置多余空间作为缓冲区. 在本节中,通过使用本文构建的一种针对 2维地理空间信息数据进行多层切片递归的空间索引树构造算法MSR,然后再利用不同量级以及不同城市的地图数据测试MSR算法性能,并且与传统的STR算法[36]、STR-网格混合索引(STR_GRID)算法[12]以及EGRQ算法[37]进行实验对比.在硬件方面,实验设备为联想Y700-15ISK电脑,搭载的是Windows10操作系统,基本配置为i7-6700HQ 4核处理器,处理速度为主频2.6 GHz超频至3.2 GHz,256 GB固态硬盘+1TB机械硬盘,RAM的容量为16 GB. 本文分别使用北京市道路网数据、天津市道路网数据和全国道路网数据构造MSR算法、STR算法、STR-网格混合索引算法(STR_GRID)以及EGRQ算法这4种算法的空间索引结构,以区域查询耗时作为衡量算法优劣的指标,详细的道路网络数据信息如表1所示: Table 1 The Data of Experiment表1 实验数据 通过表1可以得到,北京市的道路数量为84 543条,全国路网数据量为2 668 904条,其数据量非常巨大,天津市的道路数量最小.图4展示了北京市的道路网络图.城市道路具有鲜明的特点,其形状多种多样,数据由2维的经纬度坐标组成.图4以北京市的城市交通路网数据为例,绘制北京市道路网络图,其中颜色较深(蓝色)的道路为双向路,颜色较浅(红色)的为单向路,效果如图4所示: Fig. 4 Beijing road network renderings图4 北京市道路网络效果图 在本节中,首先通过使用MSR空间索引结构,对生成树的过程中叶结点的矩形框进行效果展示.如图5所示,道路网络数据为北京市道路网络数据,图5中展示了2种算法的差异,MSR算法构造的矩形框多为正方形,而不是STR算法构造的长方形. Fig. 5 Effect of MSR on the lower node of Beijing road network data图5 MSR算法在北京市道路网数据下叶结点效果展示 其次,通过实现传统的STR算法、STR-网格混合算法(STR_GRID)以及EGRQ算法作为对比实验用来验证MSR算法的优越性能,其中EGRQ算法的结果是以2为底取对数后的实验结果.本文分别从查询窗口大小、树的层次以及查询个数来测试3种算法的性能,其中树的层次即为树的层数,指的是每层结点中MBR的重叠数量.本实验中,在市级规模的道路网路数据中以0.1的差值作为经纬度网格单元的划分标准,在全国道路网络数据中以1的差值作为划分标准. 图6所示实验数据为北京市道路网络数据,当查询数目为5 000时,EGRQ算法查询性能最差,查询时间取对数后的结果为11 s;STR_GRID的查询时间为10.3 s;其次是传统的STR算法,其查询时间为10 s;MSR算法性能最优,其查询时间为9.4 s. Fig. 6 Comparison of query results under Beijing road network data图6 北京市道路网数据下的查询结果比较 图7所示实验数据是天津市道路网络数据,虽然STR_GRID的查询性能略优于MSR算法,但是2种算法的查询性能差异并不是很明显.出现这种现象的原因如下:STR_GRID是将所有的空间对象划分到各个网格中,每次构建STR树时,只是构建每个网格中包含的空间对象,所以其查询时间相对较低.MSR算法并没有进行划分网格的操作,在构建STR树时,面向的是所有的空间对象,所以其查询时间相对较高,但这种现象是很少出现的,尤其是面对大量的空间对象时,MSR算法性能优于STR_GRID.并且STR-网格算法有着固有的缺陷,该算法首先通过网格对空间区域进行划分,然后再在每个网格中构造STR树.当网格对空间区域进行划分时,将空间区域划分为多个子空间,这种划分方式全凭经验.如果对空间区域划分时,出现网格划分过细的情况,则会导致耗费磁盘存储空间和搜索时间过长,磁盘存储冗余大,造成磁盘浪费,内存利用率低;如果网格划分过细,则该方法不能很好地处理数据密度高畸变的空间区域.而MSR算法能够很好地处理数据密度高畸变的空间区域并且不会出现磁盘浪费的情况.并且MSR算法的查询性能优于传统的STR算法和EGRQ算法.所以,综上所述,MSR算法具有最优的查询及存储性能. Fig. 7 Comparison of query results under Tianjin road network data图7 天津市道路网数据下的查询结果比较 通过图6和图7可知,除了EGRQ算法的查询性能差异明显以外,其他3种算法在地市级的道路网络数据中的查询效率相差不大,3种算法的折线图走势差异很平缓,尤其是当查询数目为1 000时,3种算法的查询时间基本相当,所以猜想是道路数据量导致查询算法性能差异不明显的现象. 将4种算法运用到全国道路网络数据中,通过增加构造空间索引结构的数据量,得到的索引结构的查询结果图如图8所示: Fig. 8 Comparsion of query results under national road network data图8 全国道路网数据下的查询结果比较 图8所示的查询结果验证了猜想的正确性,空间对象数据量的增大对空间索引的性能要求更加苛刻.从图8中可以看到同为纯树型结构的STR算法和MSR算法查询效果差距较大.当查询数目为5 000时,EGRQ算法通过以2为底取对数后的查询时间为13 s;STR算法的查询时间为29.9 s,STR_GRID算法的查询时间为16.2 s,MSR算法的查询时间为14 s.在这4种算法中,MSR算法的查询时间最小,EGRQ算法查询时间最大.图8展示的实验结果再次验证了本文所提出的MSR算法在查询性能及存储性能的优越性. 图8的实验结果中,STR_GRID查询效果比STR算法效果好很多.为了找到这种现象出现的原因,本文分别统计了北京市、天津市及全国的道路网络数据在STR算法中每层树结点中的最小外包矩形框重叠个数,如图9所示. 从图9中可以很明显地发现,地市级的道路网络数据和全国道路网络数据在STR树型空间索引结构的构造过程中矩形框的重叠量存在巨大差异,尤其是在树的第1层,STR算法的MBR重叠量为108137E6,但是本文提出的MSR算法的MBR重叠量为700 123,这种差异几乎是指数级别的差距.这种现象出现的原因归结于数据结构的构建原理,这是不可避免的现象,这也是学术界在数据结构的构建问题上,体现出的一种技术瓶颈.这是2种数据的查询时间相差很大的根本原因. Fig. 9 STR algorithm overlay map图9 STR算法的重叠量展示图 最后在实验的基础上,又分别统计STR算法和MSR算法在全国道路网数据下,树型空间索引结构在树构造过程中每层树结点中的最小外包矩形框重叠个数,结果如图10所示: Fig. 10 STR tree and MSR tree layer overlay display图10 STR树和MSR树各层重叠量展示图 如图10所示,全国道路网络数据量巨大,通过对全国道路网络数据构建空间索引结构时,树结构每一层中,STR算法和MSR算法首先都根据空间对象的最小外包矩形构建树型结构.很明显地看出,树结构第1层的最小外包矩形重叠数据差距巨大,如图10所示MSR算法的最小外接矩形框重叠数量比STR算法少了近30多万个.当进行检索操作时,由于检索过程中存在检索路径不唯一的情况,从而导致检索效率很低.本文提出的MSR算法能够很大程度上减少最小外包矩形的重叠数量,而最小外包矩形的重叠数量,严重影响查询时间,MSR算法能够很好地解决这种现象,这是算法执行性能优越性的体现. 然而由于STR_GRID和EGRQ算法并不是纯树型的索引结构,所以图10展示了STR算法和MSR算法的MBR的重叠数量.STR_GRID在划分网格这一步骤中,由于其算法在空间区域内对道路网络数据进行切分,通过网格拆分庞大的道路网络数据,这种方法减少了每个网格中道路的数据量,因此STR_GRID也比STR算法的查询效率高.但是由于网格索引固有的弊端,比如网格的大小会影响到索引表的大小,如果网格太小,索引就会膨胀.网格过小不能很好地处理数据高畸变的空间区域,不但查询效率低,而且浪费内存空间.本文提出的MSR算法能够很好地处理数据密度高畸变的空间区域并且不会出现磁盘浪费的情况. 本节在这3种不同的影响因素即数据规模、构建树的层数以及查询数目的前提下,通过对这4种算法即STR算法、STR_GRID、EGRQ算法以及MSR算法进行实验对比,结果均显示MSR算法不仅减少了最小外包矩形框的重叠数量,提高了查询效率,而且又可以很好地利用内存空间,减少存储空间的浪费. 本文提出了一种对2维地理空间信息数据进行多层切片递归的空间索引树构造算法MSR.首先对地图数据划分切片,然后在单一切片内聚类对比,在相邻切片内进行聚类以此保证数据间拥有最大程度的空间邻接性;其次,按照一定范围构建叶子结点类并处理离散值;最后自下而上递归生成MSR树.实验结果表明,MSR算法不仅减少了最小外包矩形框的重叠数量,提高了查询效率,而且又可以很好地利用内存空间,减少存储空间的浪费,优于目前主流的空间索引算法STR算法、STR_GRID及EGRQ算法.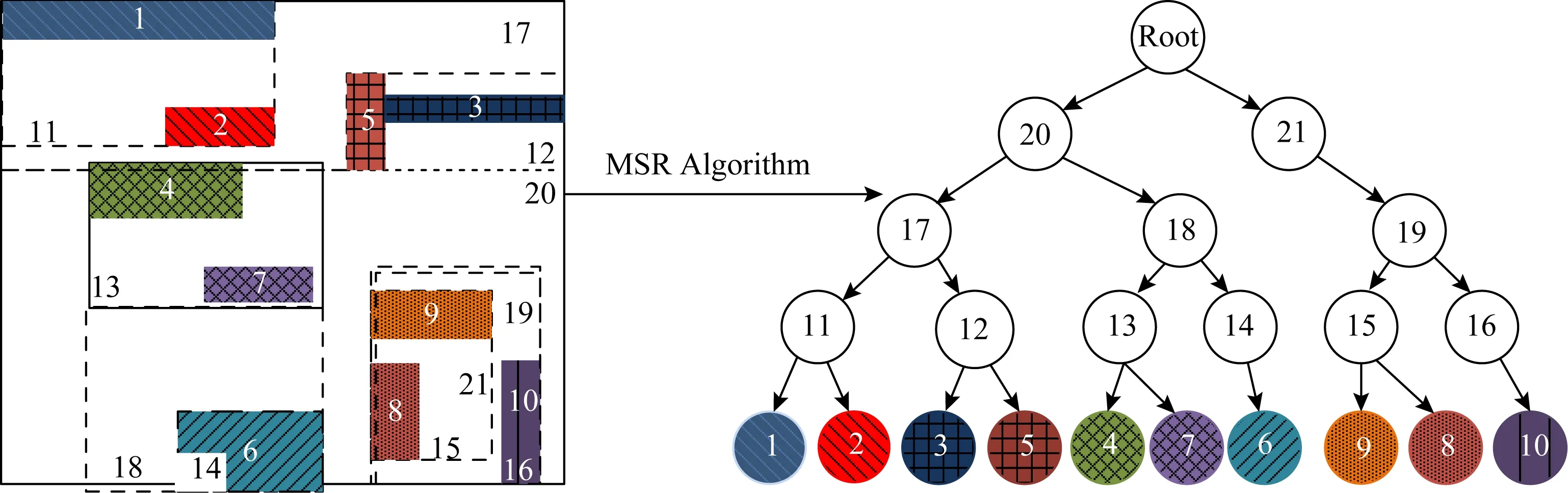
3.2 MSR算法描述
3.3 MSR树的更新和检索
4 实验与结果
4.1 数据集和算法性能度量

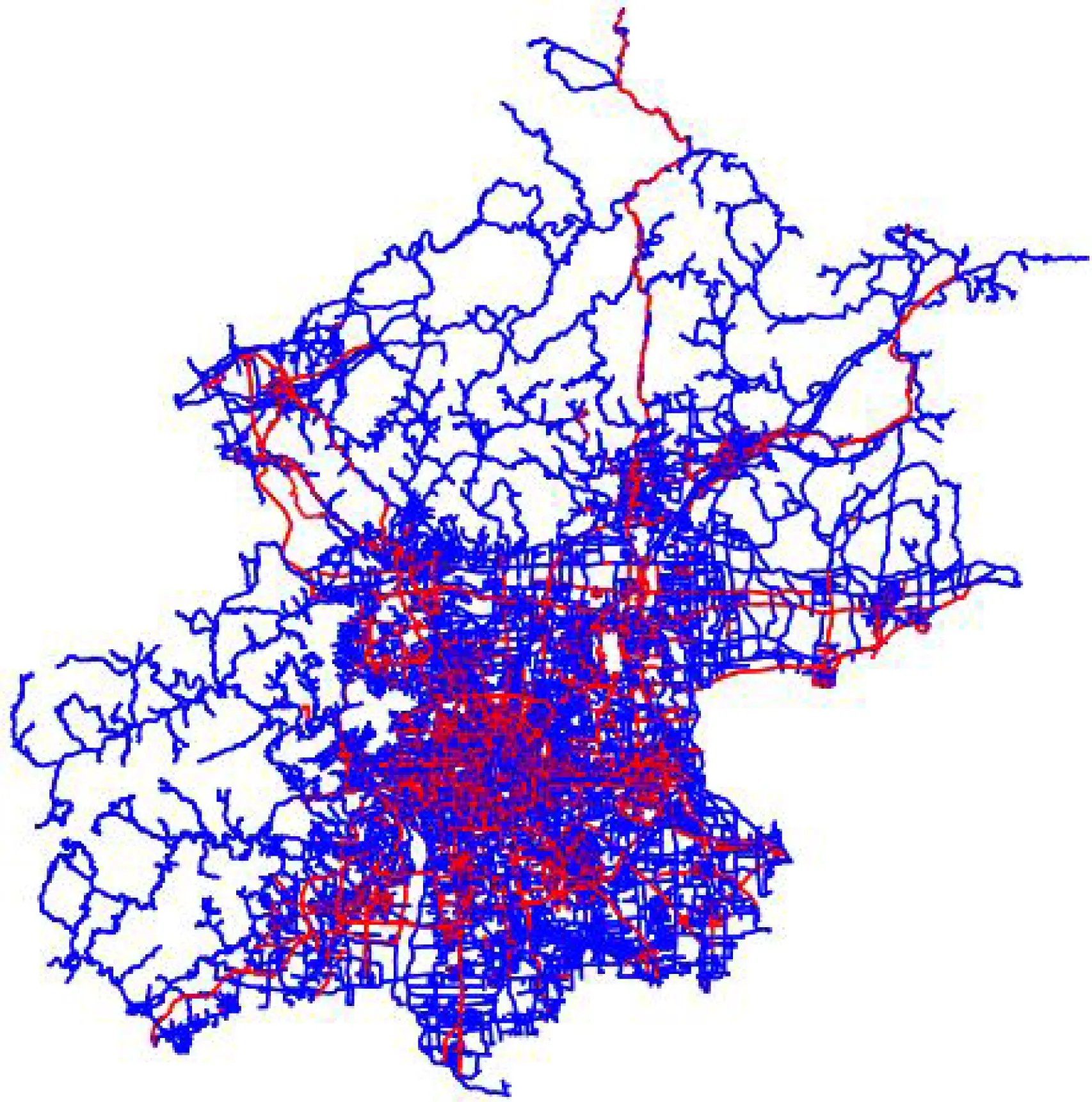
4.2 实验和结果




5 总 结
