基于多物理效应的双伸缩立柱动态特性建模仿真

2020-02-18

液压与气动 2020年2期

(1.北京天地玛珂电液控制系统有限公司，北京 100013；2.西门子工业软件(北京)有限公司，北京 100102)

引言

液压支架立柱动静态特性对其相关控制阀有直接影响。在冲击地压作用下，立柱内乳化液瞬间受压，会产生极高的冲击压力及瞬时流量，造成诸如立柱胀缸、安全阀损坏等问题[1-2]。此外，降柱阶段的高压能量释放还会引起液控单向阀卸载冲击[3]等问题。

对于立柱动态特性的理论研究，主要有直接求解数学模型[4]、基于流固耦合的有限元仿真[5-7]以及液压仿真软件建模分析等方法。前两种方法模型细致、求解精度高，但不易开展与液压阀的联合仿真；基于液压仿真软件的现有研究[8]则存在诸多简化，与实际物理过程存在一定差异。本研究在考虑立柱结构刚度、流体介质容性及惯性等因素的基础上，建立常见的双伸缩立柱仿真模型，除分析立柱压力冲击特性外，也为立柱控制阀的设计提供支持。

1 双伸缩立柱模型

拟研究的双伸缩立柱模型如图1所示，由外缸、中缸及活塞杆构成两级伸缩缸；外缸活塞腔与中缸活塞腔通过单向阀相连，活塞腔内封闭高压工作介质，形成高度分别为H1和H2的液柱。单向阀的存在保证了液压支架维持恒定支撑力，但同时将两段液柱相隔离，阻断能量传递和交换；落锤用于模拟立柱承受的冲击载荷，质量为m0。活塞杆等效为2个质量块(质量m1/2)及刚度为K1的弹簧；中缸等效质量为m2；两段液柱表示为T1和T2，初始伸出高度各为H1和H2；不考虑外缸与底座的接触刚度，视为固定端约束。

图1 双伸缩立柱的物理参数及模型

2 双伸缩立柱承受冲击载荷数学模型

2.1 落锤与活塞杆碰撞模型

落锤与活塞杆冲击作用时间短，且伴随着复杂的弹塑性变形及能量损失，机理和过程非常复杂[9]，此处利用非线性阻尼模型进行模拟[10]：

(1)

Δx=x1-x0

(2)

式中，F—— 落锤与活塞杆碰撞过程中的接触力

K0—— 反映动态接触刚度

C(Δx,δ0) —— 等效接触阻尼函数，表征碰撞过程中的能量损耗过程，由最大法向渗透深度δ0和相对位移Δx确定

x0—— 落锤的高度

x1—— 活塞杆顶部位移

2.2 中缸和外缸液柱模型

落锤冲击过程给液柱施加了阶跃输入，液柱内压力和流量剧烈变化，采用分布参数模型[11]，将液柱视作单端封闭管道，自顶向下划分为n个单元，考虑液柱的液阻、液容和液感[12]，完整反映其动态过程，如图2、图3所示。

图2 内缸和外缸液柱单元划分

图3 液柱的传输线理论模型

按传输线理论，液柱动态过程可描述为：

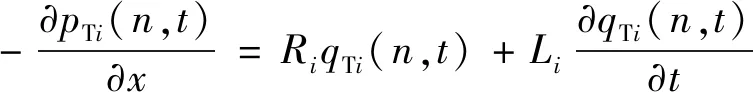
(3)

(4)

(5)

(6)

式中，pTi(n,t),qTi(n,t) —— 分别为中缸和外缸液柱内各单元处的瞬态压力和输入流量

Ri，Li，Ci—— 单位长度等效液阻、液感和液容

ρi—— 流体密度

Ai—— 流体截面积

A1—— 等效体积模量

Vi—— 液柱内单元体积

A1—— 中缸面积

A2—— 外缸面积

qT1(1,t) —— 中缸顶部1#单元的输入流量

qT2(1,t) —— 外缸顶部1#单元的输入流量

双伸缩缸的表观模量计入流体和缸体体积变形，由流体体积模量和缸体体积模量确定：

(7)

βT可根据体积模量定义，由立柱参数得出：

(8)

(9)

式中，Di—— 中缸体和外缸的外径

di—— 中缸和外缸的内径

μ—— 材料泊松比，取0.3

E—— 材料的弹性模量，取206 GPa

p—— 缸体内压力值

2.3 落锤动力学方程

(10)

式中，m0为落锤的质量，用于控制所需的冲击载荷。

2.4 活塞杆动力学方程

(11)

(12)

(13)

式中，m1—— 活塞杆等效质量，取为质量的1/3

K1—— 活塞杆的等效刚度

L1—— 活塞杆的长度

A0—— 活塞杆的截面积

B1—— 活塞杆与中缸之间的黏性阻尼系数

pT1(1,t) —— 中缸顶部1#单元压力

2.5 中缸动力学方程

(14)

式中，m2—— 中缸质量

B2—— 中缸与外缸的黏性阻尼系数

pT1(n,t) —— 中缸底部单元压力

pT2(1,t) —— 外缸顶部单元压力

3 双伸缩立柱液压仿真模型

3.1 系统建模

基于前述数学模型，采用流体仿真软件对双伸缩立柱进行建模和求解：采用线弹性接触模型LSTP00A来模拟落锤对活柱的冲击作用；采用相对运动模型MAS30完成双伸缩缸模型；考虑结构刚度、流体惯性的油缸组件，通过可变容腔组件(BRP17、BAP12)与管路(HL042)组合来完成。中缸和外缸自顶部向下，各划分为5个单元如图4所示。

双伸缩立柱采用ZF2800/16/32液压支架参数，一、二级缸径为200/160 mm，一、二级柱径为190/130 mm，外缸壁厚40 mm；活塞杆直径100 mm，长度1000 mm；支架初撑力989100 N(31.5 MPa)。活塞杆和中缸初始伸出量各为0.7 m；落锤质量5000 kg，落锤与活塞杆距离为2 m。流体介质密度为1000 kg/m3，体积弹性模量1400 MPa。

3.2 模型验证及结果分析

1) 立柱初撑压力及下沉量

对双伸缩立柱模型施加斜坡载荷信号，外力在10 s内增加至989100 N，模拟立柱在初撑力作用下的压力及下沉量。如图5所示，在模拟力作用下，立柱内液柱受压，产生支撑压力，外缸达到31.55 MPa，中缸为49.19 MPa，与支架参数相符。

图4 双伸缩立柱液压模型

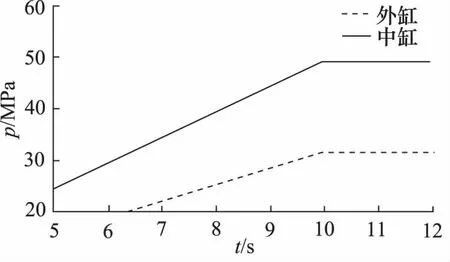
图5 内缸和外缸液柱压力曲线

在模拟力作用下，立柱内液体体积压缩，外缸和内缸结构膨胀，立柱产生一定下沉量。表1中的对比数值显示，计及中缸及外缸结构刚度后，立柱下沉量有所增加，表观弹性模量βe减小。

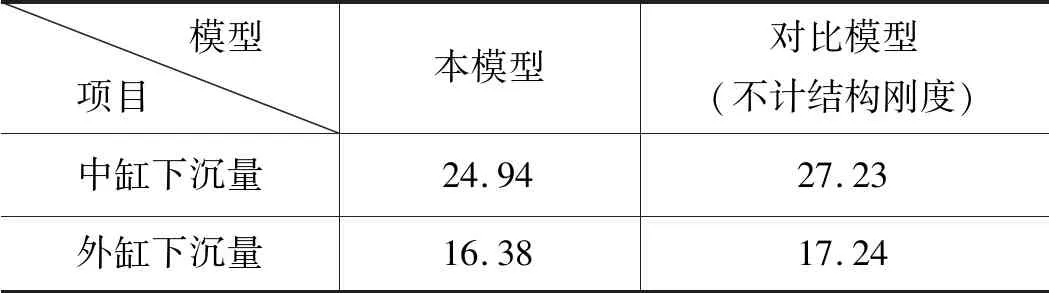
表1 不同模型下中缸与外缸下沉量 mm

2) 冲击载荷作用下立柱内压力动态过程

在模拟力作用下，立柱压力基本达到稳态后，释放落锤，对冲击载荷作用下立柱内的压力动态过程进行计算，结果如图6～图9所示。

图6 内缸和外缸液柱冲击压力曲线

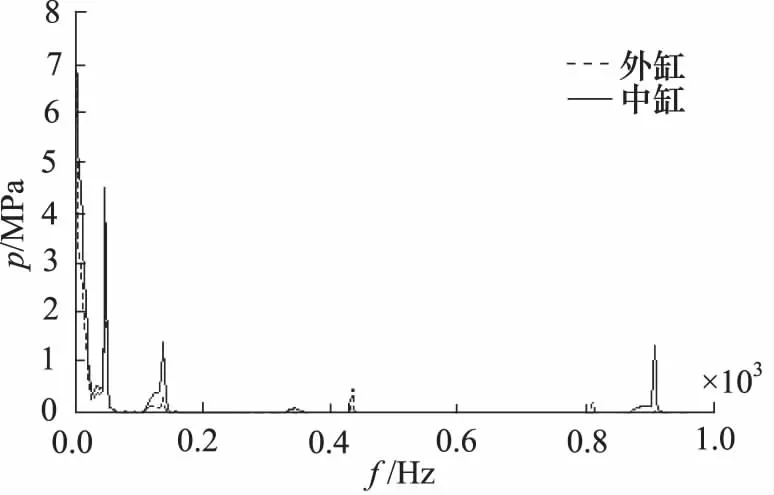
图7 内缸和外缸液柱冲击压力FFT频谱

图8 外缸液柱顶部和底部压力曲线

图9 外缸液柱顶部和底部压力曲线(冲击起始)

图6中，外缸和内缸在冲击载荷作用下，以压缩性为主，压力短时间急剧升高，远超工作阻力，外缸最大压力达到100 MPa，内缸最高压力可达165 MPa，冲击压力半周期约49 ms，此后迅速振荡衰减(61.5 Hz)，动态过程与文献[13]中试验数据相符(冲击压力峰值则受碰撞模型参数影响较大)。

由图7和图8可以看出，冲击过程引起的压力波沿缸内传递和反射，附加了约845.3 Hz(内缸)、916.7 Hz(外缸)的谐波，峰-峰值3 MPa；图9中，由于流体惯性的作用，冲击初始瞬间，外缸底部压力落后于顶部约0.5 ms，形成1 MPa压差。该时间延迟及压差主要由表观弹性模量、液体密度及液柱高度决定，对于大采高液压支架，此效应将更为显著。