钢卷仓库中多吊机调度问题的模型与算法
2020-02-18郑勇跃
谢 谢, 周 莉, 郑勇跃
(1. 沈阳大学 装备制造综合自动化重点实验室, 辽宁 沈阳 110044;2. 中国标准化研究院 社会信用研究室, 北京 100191;3. 辽宁省检验检测认证中心 事业发展中心, 辽宁 沈阳 110032)
在传统的制造过程中,人们往往只注重生产设备的加工及流程优化.对于国民经济具有支柱性的钢铁工业具有生产周期长,资源和能源消耗大,生产成本高的特点.钢铁工业生产的各个工序之间都存在着各类运输问题:钢铁工业中炼铁前原料场需要吊机运输各类原料物资;炼铁与炼钢之间需要吊机、鱼雷车、台车等进行运输;炼钢环节需要吊机运输铁水和废钢;炼钢到连铸之间的钢水需要用吊机和台车衔接进行运输;热轧阶段板坯和冷轧工序中的板卷都需要吊机和台车、汽车进行联合运输等,如图1.在各类生产环节中,吊机是一类大型、重要的衔接设备,它启动成本高,运输只能在特定的轨道上,由于钢铁工业中的被运件多数都具有温度高、单价大、各工序的送达时间由于连续运作而要求苛刻的特点,因此,钢铁工业通过吊机进行运输及装卸操作是最重要的环节.有效地对吊机进行协调,将有助于降低能耗、提高生产设备和其他各类运输工具的效率、保障实时性要求和生产的顺利进行.

图1 钢铁工业物流的总体结构Fig.1 Structure of logistic in steel industry
本文从钢铁工业冷轧后库提炼出一类多吊机调度问题,轧制后(冷轧或热轧)的板卷由卡车运输,再由吊机根据客户或订单的需求将板卷放在仓库内的指定位置.图2给出了多个吊机同时操作一台卡车的图示.每台吊机架设在仓库区域上方的轨道上,吊机可以沿轨道方向、沿轨道之间的跨间来回移动,同时吊钩可以在垂直地面的方向上下移动.在仓库内吊机或者从卡车将板卷放置在仓库指定区域内,或者根据客户订单的需求从仓库区域装载到卡车上.吊机完成指定部分的工作量后,会接着等待下一个任务.如果没有进一步的作业,吊机将等待在它们现在的位置.当卡车上的板卷装卸完,卡车就离开仓库.我们的目的是决策每个吊机的调度路线以卸载卡车上的所有板卷.
吊机调度问题是近年来的热点研究方向,相关研究的背景主要集中在港口集装箱码头、电镀生产线以及钢铁企业中.不同背景下的吊机运行方式类似,即这类大型贵重设备都架设在轨道上,同一轨道上的相邻两吊机必须保证安全距离,彼此之间不能交叉跨越.Daganzo[1]首次研究了港口码头的吊机调度问题,建立了数学模型,然而并没有考虑吊机间的不碰撞.Bierwirth等[2-3]研究了有关港口集装箱码头吊机调度问题的分类.此外,一些学者研究了吊机与其他运输工具联合作业的集成调度问题,Zhen[4]等针对两类吊机的集成调度问题建立了数学模型和启发式算法.在钢铁企业中对吊机调度问题的研究相对较少.谢谢等[5]研究了板坯仓库中的单吊机调度问题,并对该问题提出一个混合亚启发式算法求解.有关多吊机调度问题,谢谢等研究了双吊机[6]和多吊机[7]调度问题.尽管研究了多吊机调度问题,求解的算法也仅对算法的性能从理论分析的角度给出评价,很少对多吊机调度问题建模并求解,也很少提出基于分散搜索的智能优化算法.
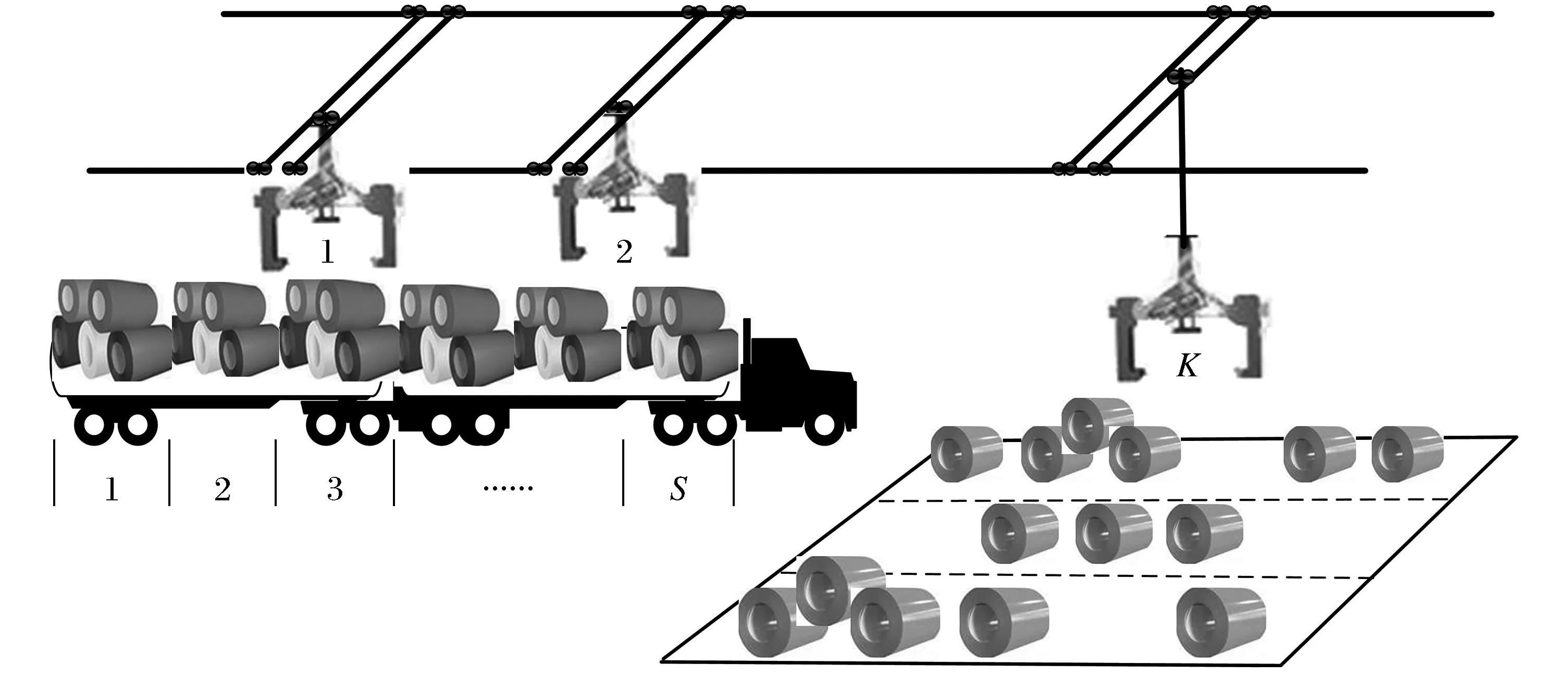
图2 钢卷仓库吊机调度示意图Fig.2 Diagram of crane scheduling in steel coil warehouse
本文建立了求解钢卷仓库多吊机调度问题的一个数学模型,模型中考虑了吊机间不碰撞的约束,证明了问题的复杂性,进一步分析了问题的性质,并提出一个基于分散搜索的启发式算法,并给出了数值计算结果,数值计算实例证明所提出的模型和算法可以应用于实际.
1 问题定义和描述
给定K个吊机和一台卡车,并假设吊机的服务时长为T.根据吊机间的安全距离,将卡车划分为S个区域,每个区域包含一组被吊板卷.每一个区域的工作量为wj,j=1,2,…,S.这里区域的工作量定义为需要从每个区域吊到仓库目标位置的板卷数目.每一区域在同一时间只能有一个吊机在作业,任意两吊机之间不可发生碰撞或交叉.即两个吊机不能在同一时间同一区域操作.当一台吊机开始在某一区域作业,直到它卸载完全部的板卷才能停下来.在本文中,由于任意两点之间的距离已知,根据吊机的行驶速度,为了方便表达,定义吊机从卡车上一个区域移动到另一个区域的行驶时间是一个常数v.各吊机具有相同的服务效率μ,即吊机单位时间内的装卸工作量(很容易扩展为各吊机服务效率不同的情况).目标函数为最小化服务卡车的最大完工时间Cmax.此外,如果吊机在区域j可用,使用二元变量bj表示吊机所处的原始位置.即
令二元决策变量xjt表示在t时刻的开始区域j仍然有工作量剩余,
令二元决策变量wjt表示在t时刻的开始区域j的剩余工作量,
MinimizeCmax
(1)
Subject to
txjt≤Cmax,1≤j≤S, 1≤t≤T.
(2)
wjt-Mxjt≤0,1≤j≤S, 1≤t≤T.
(3)

(4)
(5)
1≤j≤S, 2≤t≤T-1.
(6)
(7)
(8)
1≤j≤S, 2≤t≤T.
(9)
(10)
(11)

1≤j≤S, 2≤t≤T-1.
(12)
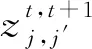
(13)
xjt∈{0, 1},1≤j≤S, 1≤t≤T.
(14)
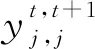
(15)
wj,t≥0,1≤j≤S, 1≤t≤T.
(16)
式(3)中M是一个足够大的数.目标函数(1)是完成所有工作量的极小化时间表长,即最后一个吊机装卸完成的时间.约束(2)表示吊机工作区域的最后完成时间,即时间表长.约束(3)表明t时刻是否有剩余板卷留在区域j.约束(4)表示工作量流平衡约束.对每一区域j,初始工作量满足wj,1=wj,接下来的每个时间段,如果在某时间内某一区域有一个吊机在工作的话,剩余的工作量将减少μ个单位,直到达到零为止.约束(5)~(8)是网络流守恒约束.约束(9)表示在某一时间内某一区域至多只有一个吊机在操作.约束(10)表示吊机间不能彼此交叉碰撞.约束(11)表示在t时段内可有一个吊机在区域j空闲.约束(12)表示吊机无中断的约束.约束(13)~(16)保证了决策变量的二元性和非负性.

2 问题性质和启发式算法及最坏性能分析
1) 问题性质.
性质1 本文所研究的问题是强NP-难的.
如果不考虑相邻区域间的移动时间,即我们所研究问题的特例,该问题为旅行商问题,明显本文的问题也是NP-难的,因此,很难在短时间内找到一个大规模实例的最优算法.
本节提出了保证吊机操作的可行解性质.吊机调度不可行通常发生在如下2种情况下:①当前吊机繁忙,板卷等待操作,此时没有可利用的吊机;②一台吊机结束当前操作后与另一台正操作的吊机发生冲突.为了简化表达,令sj表示吊机开始运输区域j内任务的时间;ej表示吊机结束运输区域j内任务的时间.
性质2 同一个吊机对两区域内板卷操作满足如下条件时,吊机调度可行.
证明 情况①,如果si>sj,那么si>ej;情况②,如果si 性质3 相邻两吊机对同一区域内板卷操作满足如下条件时,吊机调度可行. (sj-si)(ej-si)(sj-ei)(ej-ei)≥0. 证明 情况①,sj>si、ej>si、sj>ei、ej>ei,表明只有当区域i的操作完成时,区域j才开始;情况②,sj>si、ej>si、sj 2) 基于分散搜索的启发式算法.基于以上可行性质,提出基于分散搜索(scatter search)的启发式算法. 分散搜索算法是一种基于种群的智能优化算法,它的基本思想是对参考集中解的质量和分散性进行控制,进一步对解进行组合,为了提高解的质量,该算法可以利用局部改进搜索策略,通过多种搜索方式,从而提高求解质量.分散搜索算法由Glover[8]于1977年首次提出,但直到1998年,Glover[9]才将整个算法过程系统地进行了总结.图3给出分散搜索算法基本流程图.图中PSize为预先给定的初始种群,b为预先给定的参考集RefSet,MaxIter表示迭代的最大次数,MaxSubset表示选定的子集总数,NewElements表示参考集是否被更新. Step 1 初始化.设置PSize,MaxIter,b,设置NewElements=FALSE,Iter=0;将吊机按从小到大的顺序编号. Step 3 在集合Refset中检验如下条件:①(sj-si)(ej-si)≥0;②(si-sj)(ei-sj)≥0;③(sj-si)(ej-si)(sj-ei)(ej-ei)≥0,从而构造子集NewSubsets. Step 4 置Iter=Iter+1.若Iter>MaxIter,则算法停止;否则,在NewSubsets中选择可行解子集s,采用解组合方法对s里的解进行组合,产生新解x. Step 5 采用如下方式进行搜索:①当吊机完成各自区域内任务时,依次计算相邻吊机当前剩余任务量,选择剩余任务量大的区域分配给当前吊机;②如果相邻区域吊机未完成工作,则等待直到该吊机空闲;利用此方式搜索改进当前解并得到新解x′. Step 6 如果当前解优于参考集中质量最差的解时,则将该改进解放入候选集合中,以备更新参考集. Step 7 将子集s从NewSubsets中删除.若NewSubsets为空,则转入Step 8;否则,执行Step 5. Step 8 更新参考集.从候选集中选择质量优的解并替换当前参考集中质量差的解,然后执行Step 4;若候选集为空,则算法停止. For (Iter=1到MaxIter) 步骤1: 生成初始种群P, |P|=PSize. 步骤2: 从P中选择b个具有代表性的解, 产生参考集合RefSet. While (NewElements=TRUE) do 步骤3: 从参考集中选定子集, 置NewElements=FALSE. For (SubsetCounter=1, …, MaxSubset) 步骤4: 置NewElements=FALSE 步骤5: 取出第SubsetCounter个子集s. 步骤6: 对子集s应用解的组合策略获得一个或更多的新解xs. 步骤7: 对解xs应用解的改进策略获得改进解x's. 步骤8: 更新参考集. 若参考集被更新, NewElements=TRUE, 跳出循环. End For End WhileEnd For (17) (18) 即 因此该算法的最坏性能比是2,而最坏情况分析只表示算法在极端情况时的性能.因此,在下一节中将通过计算实验验证算法的平均计算性能. 针对以上启发式算法,使用C++语言开发了算法程序,为了验证所提出算法的有效性,通过模拟实际数据,随机产生了一系列的实验数据进行验证.实验环境如下. 1) 硬件环境:Dell Optiplex (CPU:Pentium Ⅳ 3.0 GHz,内存:1 GB). 2) 软件开发环境:微软VC++6.0开发平台. 3) CPLEX 11.0优化软件. 算例的各参数产生方式如下:根据实际问题背景,吊机的数目K分别取2,3,5,8,10;针对每次吊机个数的不同取值,卡车的分区S分别取4种对应数值;区域的工作量wj在[10,20]之间根据均匀分布随机产生.吊机的行驶时间v和服务效率μ根据均匀分布分别在[5,10]和[4,8]之间产生.根据每类数值的组合,共有20个实例,每个实例随机产生10组数据来验证MILP模型和启发式算法的有效性.表1中列出的结果是每个实例的平均值.其中“—”表示使用CPLEX软件在预先设定的7 200 s内没能求出问题的最优解.为了验证算法的性能,用最优偏差Opt.gap进行度量,如果MILP模型求出了问题的最优解,Opt.gap=(CA-C*)/C*·100%;如果MILP模型在预先设定时间内没能求出问题的解,则通过松弛所建立数学模型的约束(12)获得问题的下界.此时Opt.gap=(CA-CL)/CL·100%表示问题最优解与下界的相对间隙. 表1 混合整数线性规划(MILP)模型和启发式算法的计算结果 依据表1的结果,可以得出如下结论. 1) 当吊机数目不超过5,卡车分区不超过8的小规模计算实例,基于分散搜索的启发式算法与MILP的平均偏差小于1%,即使全部算例中的最大计算偏差也小于0.50%.此外,从所消耗的计算时间来看,启发式算法与MILP的性能是可以比较的.然而,对于MILP中稍微大一些的实例来说,所消耗的时间逐渐增大. 2) 当吊机数目不超过5,卡车分区超过8的中等规模计算实例,MILP模型可以求出问题的最优解,但是所消耗平均计算时间却很大,而所提出的基于分散搜索的启发式算法所消耗的时间相对较小,最长的不超过30 s. 3) 当吊机数目超过8,卡车分区超过8的大规模计算实例,虽然CPLEX软件不能在7 200 s内求得所有问题的最优解,但是它却可以提供接近最优解的下界.随着问题规模的增大,所提出的启发式算法所消耗的时间不超过60 s.计算结果显示启发式算法和MILP模型相比所获得的最大偏差不超过0.40%. 本文研究了钢卷仓库内的多吊机调度问题,针对该问题,建立了多吊机协调调度的模型,考虑了避免吊机碰撞的实际约束,为了求解大规模的实际问题,进一步提出了一个基于分散搜索算法的启发式算法,该算法可以求得问题的近优解.未来的研究将进一步考虑具有更多实际约束的该类问题,如考虑将吊机调度与钢卷位置的选择集成考虑,这是因为钢卷位置的选择将影响到吊机的调度,反之也成立.



3 计算实验结果

4 结 论
5 结 语
