基于新息异常检测的改进抗差自适应卡尔曼滤波算法
2020-02-18葛宝爽唐志坤
葛宝爽,张 海,唐志坤
(1.北京航空航天大学自动化科学与电气工程学院,北京 100191;2.国家空域管理中心,北京 100094)
0 引言
卡尔曼滤波作为一线性最优估计,被广泛地应用到导航系统与目标跟踪系统中。在状态空间模型是线性且噪声统计特性完全已知并为相互独立的高斯白噪声时,卡尔曼滤波可以得到在最小均方意义下的最优解。然而在工程实践中,由于外界环境的干扰,量测噪声统计特性通常是未知或时变的,在此情况下将无法直接使用标准卡尔曼滤波(Standard Kalman Filter, SKF);另外,量测中不免会含有异常值,由于SKF自身不具有抵抗异常值的能力,这就导致尽管很少的量测异常便会引起滤波振荡,致使滤波精度下降[1]。
针对工程实践中面临的量测不稳定问题,SKF有不同的改进方案,如:适用于模型参数或噪声统计特性未知的自适应卡尔曼滤波(Adaptive Kalman Filter, AKF)[2-3];结合抗差估计理论的抗差滤波[4-5]等。在卡尔曼滤波中,新息作为滤波中的关键量,含有量测的全部信息,并且对异常量测值极为敏感。因此,无论是在AKF还是抗差滤波中,经常利用新息的特性估计量测噪声方差或异常检测,以期在保证滤波精度的前提下提高算法的鲁棒性与容错性。
文献[6-7]利用新息正交特性对量测中的异常值进行辨识,然后利用抗差估计理论中的Huber方案构造等价权函数(活化函数),并引入到卡尔曼滤波算法中,该活化函数通过降低量测异常值的权重提高了组合导航系统的抗差性能。文献[8-9]依据新息服从多维正态分布的特性,采用3σ准则对量测异常值进行辨识,随后通过调节滤波增益阵减弱异常值对滤波结果的影响。文献[10-11]依据概率统计知识,构造新息的卡方统计量,并成功地应用到目标跟踪与组合导航的异常值检测中。虽然文献[10]从理论上证明了所构造的等价权函数能够保持新息的特性不变,但在实际应用中因其需要计算矩阵平方根的逆,存在数值稳定性问题;文献[11]将Huber方案构造的等价权因子与卡方检验的临界值相结合构造了新的方差膨胀因子,当量测异常发生时,通过方差膨胀因子放大量测噪声方差阵降低了异常量测权重,因此增强了滤波的抗差性能。文献[12]将AKF与抗差估计理论相结合,利用抗差估计理论构造等价权因子的方法构造了AKF中的自适应调节因子,并利用新息构成的统计量实时检测调节量测等价权矩阵,以平衡状态预测与量测间的权重。文献[13]在保留移动开窗法估计量测噪声方差阵的同时,引入了自适应因子来调节量测异常值对整个滤波系统的影响,较SKF提高了滤波精度且增强了滤波稳定性。
以上有关卡尔曼滤波改进算法的研究具有一定的理论意义和工程实践应用价值,并且能够较好地应对量测噪声统计特性未知及量测中的孤立型异常值。但是,量测中连续型异常值的出现严重制约了上述算法的应用范围与滤波效果。为此,本文首先从新息的角度分析了量测异常对滤波结果的影响;随后,针对工程实践中量测噪声统计特性未知且含有连续型异常值的情形,构造了鲁棒性更强的自适应Sage-Husa滤波算法;通过仿真实验比较了改进算法与常规抗差自适应滤波算法的性能,验证了改进算法抑制量测异常的有效性。
1 卡尔曼滤波量测异常影响分析
考虑量测中含有异常值的离散状态方程为
Xk=Φk,k-1Xk-1+Wk-1
Zk=HkXk+bk+Vk
(1)
式中,Xk为状态量,Φk,k-1为状态转移矩阵,Zk为量测量,Hk为量测矩阵,bk为异常量测,Wk-1与Vk为相互独立的高斯白噪声。

(2)

当bk=0时,式(2)便退化为SKF;当bk≠0时,即量测中含有异常值时,由式(2)中的新息定义可知,量测中的异常值必然引起新息的异常,受异常值污染的新息不仅会使当前时刻的滤波精度下降,同时还将会通过一步预测值向后续时刻传递,引起滤波振荡。对于连续型异常值,若不采取必要的检测和修复算法则很可能导致滤波最终发散,不能满足导航或目标跟踪的定位要求。另一方面,由式(1)中受异常污染的量测方程可以直接看出,若异常bk表现为连续型随机噪声的形式则可看作为量测量新增加性噪声,因此会引起量测噪声统计特性的变化。
2 改进抗差自适应卡尔曼滤波
2.1 改进Sage-Husa自适应量测噪声方差估计
Sage-Husa自适应滤波算法通过对新息序列或残差序列进行开窗估计出当前时刻的量测噪声方差阵[14]。在基于新息与残差的开窗估计算法中,基于残差的自适应估计(Residual-based Adaptive Estimation, RAE)算法避免了基于新息的自适应估计算法估计量测方差阵时可能出现的负定现象。但RAE在估计量测噪声方差阵Rk时需要用到当前时刻的状态估计方差阵Pk,而计算Pk又需要已知Rk。为了避免上述矛盾,常规做法是采用上一时刻的状态估计方差阵Pk-1来代替Pk,如式(3)所示
(3)

考虑量测异常的影响,本文采用模值更大的预测方差阵Pk/k-1来代替原算法中的Pk-1阵,对Rk估计时起到放大作用,以降低异常量测权重。改进后的估计算法如式(4)所示
(4)
2.2 改进自适应滤波稳定性分析
改进后的Sage-Husa自适应滤波在估计量测噪声方差时采用了当前时刻的预测方差阵Pk/k-1。为了证明改进后的自适应滤波算法仍然是滤波稳定的,首先给定如下假设条件:原系统可控、可观且对任意时刻k>0有

(5)


(6)
2.3 改进抗差估计策略
尽管Sage-Husa自适应滤波算法可以对时变噪声方差进行在线估计,但其对量测中的异常并无抵制能力。为此可将抗差估计的思想引入到Sage-Husa滤波中以构造具有抗差能力的自适应滤波算法。
由多元正态分布的基本性质可知p元正态分布是p个相互独立的一维正态变量的联合分布,据此可依据新息服从多元正态分布的特性对量测异常进行逐维检测判别。另受IGG函数与Huber函数的启发,构造如下权函数
(7)
式中,c0可取(0.8~1.5)σi,c1可取(3.0~5.0)σi,σi为第i维新息标准差。K(:,i)=0表示将卡尔曼增益阵的第i列元素置零。
由式(7)可知,抗差权函数的降权区采用了较为简洁的Huber函数降权形式。拒绝区则不同于原IGG函数直接将新息置零,而是将加权异常新息的滤波增益置零,由此可在抑制新息异常的同时调谐状态估计方差阵。改进的拒绝区避免了连续异常出现时新息持续置零,但未相应调节状态估计方差阵致使其不能反映当前时刻受异常影响滤波估值的可信度,最终导致滤波发散的情况。
2.4 改进抗差自适应滤波方案
改进抗差自适应卡尔曼滤波(Improved Robust Adaptive Kalman Filter, IRAKF)算法流程如图1所示。

图1 改进抗差自适应滤波方案Fig.1 Improved robust adaptive filter scheme
图1中,C为阈值因子。由图1可知,改进的抗差自适应滤波算法分为两部分。第一部分为抗差Sage-Husa自适应滤波,在开窗估计量测噪声方差的同时,利用所构造的三段权函数依据新息的不同幅值对其施加权重以控制量测异常的影响;另外,为了避免因开窗估计调节量测噪声方差引起漏检率升高,第二部分采用SKF中的新息辅助量测异常检测,当检测出量测异常时,直接通过软件方式实现卡尔曼滤波增益阵列置零。经过双重检测可以有效地控制量测异常对滤波结果的影响。
3 仿真验证
为了能够验证本文所提IRAKF算法对不同类型量测异常的抑制能力,本文以目标跟踪为例进行了仿真验证实验,并与SKF及现有抗差自适应滤波算法如基于残差的抗差自适应滤波(Robust Residual-based Adaptive Estimation, RRAE)[16]、自适应抗差卡尔曼滤波(Robust Adaptive Kalman Filter, RAKF)[17]、简化抗差Sage-Husa自适应滤波(Robust Simplified Sage-Husa Adaptive Kalman Filter, RSSHAKF)[18]算法的滤波精度作了比较。
在仿真实验中,系统状态量为二维位置与速度,即X=[x,Vx,y,Vy]T,状态初值设为X0=[1.25×105m,-100m, 1.25×105m,-100m]T。状态空间方程如下
Xk=
(8)

仿真实验1中,在x轴位置量测20~70历元间,每隔5个历元叠加均值为10,方差为64的孤立型异常值。仿真实验2中,在x轴位置量测50~70历元之间,加入均值为0,方差为64的连续型异常干扰。针对以上两种情况,分别进行100次Monte Carlo实验,仿真结果如图2和图3所示。滤波结果均方根误差(Root Mean Square Error, RMSE)定义如下
(9)


(a) X轴位置滤波误差

(b) X轴速度滤波误差

(c) Y轴位置滤波误差

(d) Y轴速度滤波误差图2 孤立型量测异常滤波误差Fig.2 Filtering errors with isolated outliers in measurement
由图2(a)和图2(b)可知,当出现孤立型量测异常时,IRAKF能够有效抑制异常值对滤波结果的影响,说明所提算法能够提高滤波精度且具有一定的鲁棒性。SKF滤波结果产生了较大的偏差,这主要是因为其不具有抵抗量测异常的能力。RRAE算法可以有效抵制孤立型异常的干扰,并且具有自适应调节量测噪声方差阵的能力。进一步对比IRAKF与RRAE滤波的RMSE,前者位置RMSE为1.5942m,后者位置RMSE为2.1969m,IRAKF位置精度提高了27.43%。RAKF受量测异常影响严重,这主要是因为在RAKF算法中更加依赖量测值。虽然RSSHAKF能够在一定程度上抑制量测异常的干扰,但较IRAKF其效果有待提高,RSSHAKF位置RMSE为2.1818m。由图2(c)和图2(d)可知,在未有量测异常时,除RRAE算法波动较大外,其余算法滤波效果相当。
图3中仅给出了有量测异常发生时的滤波误差图。由图3可知,当连续型异常量测发生时,IRAKF仍能够有效抑制,其位置RMSE为1.4663m,速度RMSE为0.3367m/s。SKF、RAKF与RSSHAKF滤波位置最大误差均超过了10m,且在50~70历元间持续振荡。虽然RRAE滤波效果优于除IRAKF外的其他算法,其位置RMSE为1.9583m,速度RMSE为0.5475m/s,但其存在滤波发散的风险。
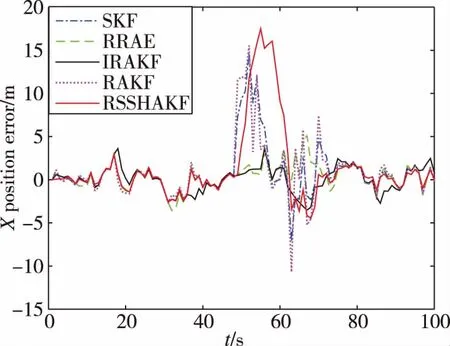
(a) X轴位置滤波误差

(b) X轴速度滤波误差图3 连续型量测异常滤波误差Fig.3 Filtering errors with continuous outliers in measurement
4 结论
本文针对卡尔曼滤波中量测异常的问题,提出了一种改进的抗差自适应滤波方案。算法分析与实验结果表明:
1)量测异常通过污染新息进一步影响滤波结果。本文所提出的改进滤波方案采用双重检测方式,通过新息统计量检测量测异常,提高了异常检测的有效性。
2)新构建的量测异常抑制权函数合理分配权重,有效控制了量测异常对整个滤波过程的影响,提高了滤波精度。
3)本文所提改进抗差自适应滤波方案,因采用了双滤波结构,因此在一定程度上增加了计算量。对一些对计算量有严格要求的工程应用,可只采用抗差Sage-Husa自适应部分以减少计算量。
