基于道路几何特征的地图匹配方法研究
2020-02-18李殿茜
刘 峰,郭 阳,郑 辛,李殿茜
(1.北京自动化控制设备研究所,北京 100074;2.国防科技大学,长沙 410000;3.中国航天科工集团有限公司,北京 100048)
0 引言
随着车载导航技术的发展,各种定位定向技术在车载导航系统中都得到了成功的应用,如卫星定位技术、惯性导航(Inertial Navigation System,INS)技术、航位推算(Dead Reckoning,DR)技术、无线电技术等,但每一种技术都有其无法克服的局限性。例如当车辆通过涵洞、隧道、立交桥时,或者卫星接收机受到遮挡、干扰时,导致卫星无法正常定位;受陀螺漂移、加速度计零偏等惯性器件误差的影响,惯性定位定向的定位误差会随着行驶时间和行驶距离的增加而增大。采用地图匹配(Map Matching)技术提升定位定向系统的定位精度,具有不需要增添新的硬件、成本低、能有效抑制误差发散等优点。因此对地图匹配相关技术展开研究具有重要意义。
地图匹配是一种基于软件技术的定位误差修正技术,依靠精确的数字地图道路信息和地图匹配算法实现道路信息与车辆定位信息之间的匹配。本文将从地图匹配的基本原理出发,针对点到线型地图匹配方法的局限性,提出了一种基于道路几何特征的地图匹配方法,并进行试验验证。
1 地图匹配原理
1.1 地图匹配基本原理
地图匹配的基本原理具体来说就是以某个车辆的定位点或某段车辆的定位轨迹作为待匹配样本,将该点或该轨迹曲线附近的所有道路上的位置点或道路曲线作为模板,通过待匹配样本与模板间的匹配,选择相似度最高的模板作为匹配结果,然后根据匹配结果,校正系统的定位输出,从而获取正确的行驶路线。图1所示为地图匹配原理图,通过惯性定位定向系统测得车辆位置或行驶轨迹,与数字矢量地图的道路数据进行比较,经过地图匹配后,找到车辆所在的道路,并且确定车辆在道路上的具体位置。

图1 地图匹配原理图Fig.1 Map-matching principle diagram
地图匹配可以看作是一个模式识别的过程。一个完整的地图匹配算法一般包括3个过程:1)确定误差区域,找出车辆附近所有待匹配的候选路段;2)从所有候选路段中确定车辆所行驶路段,即匹配路段;3)确定车辆在道路上的具体位置,即匹配点。
1.2 典型地图匹配实现方法介绍
通常所谓的地图匹配方法的不同,往往指的是确定匹配路段也就是寻找车辆所在的道路采用的方法不同,对于车辆在路段上的具体位置,确定方法相对比较单一。大多数算法在找到车辆当前行驶的路段后,只是将定位点往路段上简单地作投影,将投影点作为车辆在道路上的匹配点,实际属于点到线型的地图匹配方法。
目前典型的地图匹配算法有垂直投影法、概率统计法、相关性算法、基于网络拓扑关系算法和基于权重的算法等。这几种典型地图匹配算法的优缺点、适用范围等如表1所示。

表1 典型地图匹配算法比较Tab.1 Typical map-matching algorithm comparisons
2 基于道路几何特征的地图匹配方法
点到线式的地图匹配算法,是以比较定位点到道路的投影距离作为匹配路段选取的重要标准,这要求只有定位精度较高时才能匹配到正确的道路上,多用于辅助卫星导航定位。而且该方法只能抑制垂直于道路方向的误差,但难以修正沿道路方向上的误差。另外,每个定位点往往独立匹配,并没有充分利用历史匹配信息,当遇到野点时,容易出现误匹配,从而影响系统的可靠性及匹配精度。
不同于GPS卫星导航,当车辆采用惯性导航时,行驶过程中的定位轨迹为连续平滑的曲线,并且行驶一段里程或经过特殊路况(如拐弯、转盘等)时,轨迹往往具有明显的几何形状。在对匹配实时性要求不高的情况下,可以通过比较车辆行驶轨迹和道路之间的几何形状进行地图匹配,形成一种基于道路几何特征的线到线型的匹配方法。下面将从候选路径的确定、匹配路径的确定和最终匹配点的求取3个方面对该方法进行详细介绍。
2.1 候选路径确定
候选路径的确定就是对数字矢量地图中道路信息的筛选,缩小寻找车辆当前所在匹配路段时的搜索范围,从复杂地图路网中检索出几条道路路径作为确定最终行驶路径的候选项。候选路径的选取原则是:确保包含正确匹配路径的前提下,尽可能地减少待匹配路径的数目,以提高匹配效率。
1)检索框确定候选路径集
以惯性定位定向的定位坐标为几何中心,以固定长度为边长,构造检索框,并记录此刻的航向角,代表车辆行驶方向,其结构为(Point, SearchBox, Heading)。其中,Point为检索框中心线坐标;SearchBox为检索框边界左下和右上2个对角点坐标;Heading为惯性定位定向系统输出坐标点时刻测得的惯导航向角。利用搜索框进行空间索引,行车过程中实时搜索沿途周边一定范围内的路段,构成候选路径集。
构建的检索框如图2所示。
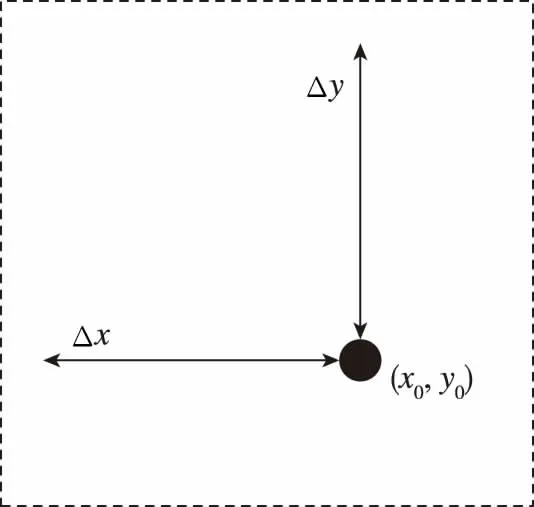
图2 检索框构建Fig.2 Build the searching box
2)候选路径的进一步筛选
由于惯性导航系统可以提供精确的车辆航向信息,所以可以通过比较航向ψ和道路方向θ对候选路径集进行进一步筛选。将候选路段集中满足Δθ<π/4(其中Δθ=|θ-ψ|)的路段重新组合为数目更少的候选路径集LL={ll1,ll2,…,llm},(m≤n),以此为基础进行后续计算。
2.2 匹配路径确定
1)利用道格拉斯-普克法处理定位轨迹
数字矢量地图中,路段信息利用折线近似曲线的方法,由能表征路段几何形状的采样点表示。其特点是,采样点分布不均匀,转弯部分采样点分布密集,直线部分采样点分布稀疏,可认为低频非定周期采样。而惯性定位定向系统输出的车辆行驶轨迹由固定周期高频采样数据组成,所以,在对定位轨迹和路径进行匹配时,在尽可能保证原有曲线形态不至于有太大改变的同时,对定位轨迹点进行抽稀处理。本文采用道格拉斯-普克法对定位轨迹进行处理,其优点是具有平移和旋转不变性,能够在保持原来波形的条件下,压缩大量的数据,如图3所示。

图3 道格拉斯-普克法处理定位轨迹Fig.3 The location trajectories by Douglas-Peucker algorithm
2)利用Frechet距离确定匹配路径
确定匹配路径,可认为是从众多候选曲线中找到和定位轨迹曲线相似性最高的那条。本文采用比较2条曲线Frechet距离的方法,Frechet距离越小,这2条曲线的相似度越高。所以取和处理后车辆定位轨迹之间Frechet距离最小的候选路径为匹配路径。
设行驶轨迹P由p个采样点组成,候选路径Q由q个采样点组成。使用σ(P)和σ(Q)分别表示两轨迹点的顺序合集,则有σ(P)=(u1,…,up)和σ(Q)=(v1,…,vq)。构造序列点对L: {(ua1,vb1),(ua2,vb2),…,(uam,vbm)}其中,a1=1,b1=1,am=p,bm=q,对于任意i=1,…,q有ai+1=ai或ai+1=ai+1和bi+1=bi。
P、Q轨迹点之间的序列对之间长度定义为各序列对中欧式距离的最大值,表达式如下
(1)
那么其离散Frechet距离为
(2)
使用Frechet距离进行路径选择的方法具有一定的适用范围,实际应用中,初始对准时装定较高精度位置信息,车辆启动后,每隔一定里程(5~10km)做一次匹配,将匹配结果和定位结果的误差量作为修正量,对后续定位信息进行修正,进而提高导航精度。
2.3 匹配点的求取
对图3所示路段上各特征点求其曲率,如图4所示。经分析知,对于几何特征明显的路段,其采样点曲率变化规律由最小值A不断增加到最大值B,然后不断减小到最小值C。

图4 路径几何特征点曲率变化规律Fig.4 Geometric feature point curvature variation rule
依次求取定位轨迹点序列和匹配路段点序列中各个点的曲率,并对其进行如下处理:当某点曲率大于某阈值η时,用其上述所对应的A、B、C这3个特征点表示该段。以此类推,将车辆轨迹拆分成若干段,每一段都由上述的3个特征点表示。
假设定位定向轨迹和匹配路径分别由m和n个特征段构成。在匹配路径特征段中选取一段P1作为模板特征段,在轨迹特征段中选取一段P2作为待样本特征段。则具体匹配过程如下:
1)求最佳模板特征段
如图5所示,定义T为空间两点之间的平移向量;P2经过平移变换T得到特征段P3,使得P3和P1有共同的原点m2。θ1和θ2被定义为惯导轨迹特征段到匹配路径特征段的旋转角。定义W=|θ2-θ1|为P1和P2旋转角度量参数,分别计算P2与匹配路径的各个特征路段的匹配度,得到一个评价空间Q={W1,W2,W3,…,Wm}。求取Q中的最小值 ,那么P2与道路中的第k段为最佳模板特征段。

图5 特征路段匹配示意图Fig.5 Schematic diagram of matching between two characteristic sections
2)计算匹配参数
如图5所示,样本特征段P2到最佳模板特征段P1的匹配参数包括1个平移参数T、2个旋转参数R1和R2,以及1个拉伸参数S,各自求取公式如下
(3)
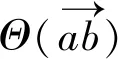
3)求匹配点
设以特征段为骨架的定位轨迹上的任意一点为P,P*为经过匹配参数变换得到的的匹配点,则有
(4)
式中,当P在n2以前或在n2上时,θ=θ2;当P在n2以后时,θ=θ1。
3 试验验证
1)图6~图8所示依次为车辆行驶过程中,经过检索框索引确定的候选路段(红色)、利用航向角筛选后的候选路段和最终匹配路径。
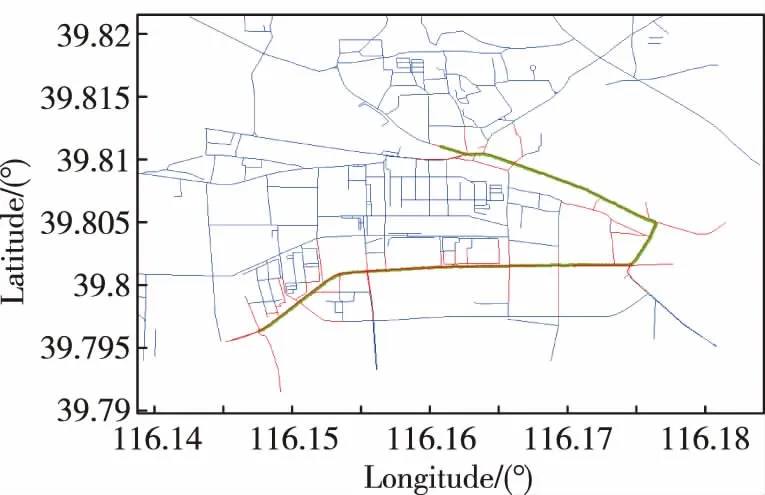
图6 检索框确定候选路径集(红色)Fig.6 The candidate path(red lines) determined by searching box

图7 航向信息近一步筛选候选路径集(红色)Fig.7 Candidate paths further filtered by direction
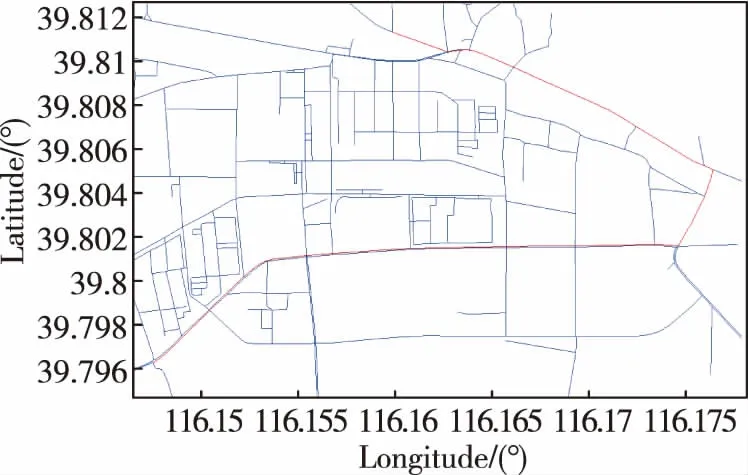
图8 匹配路径的确定(红色)Fig.8 Matching path determination
可以看出,该算法可以有效地确定候选路径,并准确和车辆行驶轨迹对应的路径匹配。
2)以道路地图为背景图,将GPS卫星定位(精度≤1m)、惯性定位定向系统输出以及地图匹配得到的行车轨迹进行比较,如图9所示。

图9 一段行车轨迹的匹配结果Fig.9 Matching result of a driving track
以GPS卫星定位数据为基准,分别求取纯惯性定位和地图匹配修正后的位置误差,误差曲线如图10所示。

图10 地图匹配前后位置误差对比Fig.10 Comparison of position errors before and after map matching
从图10中可以看出,利用地图匹配可将经度误差从49m提高到20m,纬度误差从65m提高到15m,证明了该算法可以达到较高的匹配精度。
4 结论
有效的匹配方法是实现地图匹配的核心,目前典型算法简单的匹配精度低、可靠性较差;匹配准确性高的计算复杂,匹配效率差。
本文利用惯性导航轨迹连续、航向信息准确的特点,设计了一种基于道路几何特征的地图匹配方法。通过比较车辆行驶轨迹和道路之间的几何特征进行地图匹配,经验证该方法可行,且可达到较高的匹配精度。
