基于VAR模型的CPI与PPI因果关系检验
2020-02-14李秋玲王智文张灿龙庚佳颖安晓宁
李秋玲 王智文 张灿龙 庚佳颖 安晓宁


摘要:选取国家统计局1996年10月-2019年2月公布的CPI和PP1月度同比数据,通过构建向量自回归(VAR)模型,运用格兰杰因果关系检验、脉冲响应函数以及方差分解法,研究CPI与PPI之间的动态关系。研究结果表明:在选用的滞后期为2的VAR模型中,CPI与PPI互为因果关系,它们之间保持着相互影响的正向时滞关系:CPI与PPI受到自身的冲击影响较大,而且二者对自身有正向的影响;CPI的变动90%由自身引起,10%由PPI引起,PPI的变动80%由自身引起,20%由CPI引起。因此,在研究CPI与PPI的变动问题时,应重点关注自身变动,同时注意相互影响。
关键词:CPI;PPI;VAR模型;脉冲响应;方差分解
中图分类号:O212.1;F222.33DOI:10.16375/j.cnki.cn45-1395/t.2020.01.016
0 引言
CPI(Consumer Price Index)是反映一定时期内城乡居民所购买的生活消费品和服务项目价格变动程度和趋势的相对数。PPI(ProducerPriceIndex)是一定时期内全部工业产品出厂价格总水平的变动趋势和程度的相对数。CPI与PPI是反映社会一般物价水平与宏观经济状况的重要指标,对政府制定经济政策以进行宏观调控具有相当重要的参考价值,保持CPI与PPI的相对稳定并把两者控制在一个合理的范圍内也是中国人民银行实施货币政策的一个核心目标。因此,CPI与PPI两者之间的传导机制受到了业界与学术界的广泛关注,到目前为止,国内已经有许多的学者研究了CPI与PPI的传导关系,但是由于所使用的方法以及研究的时期不相同,得出的结论也不尽相同。
在我国CPI与PPI之间的传导关系的研究中,大多数是基于VEC(Vector Error Correction)模型或者VAR(Vector Autoreg Ressive)模型研究两者之间的线性格兰杰因果关系。贺力平等Ⅲ使用CPI和PPI的同比数据和定基数据,基于VAR模型探讨了2001年1月-2008年7月CPI和PPI之间的格兰杰因果关系,研究发现:CPI是PPI的格兰杰原因,价格由下游(CPI)传导到上游(PPI)。徐伟康应用VEC模型考察与贺立平等Ⅲ所使用的CPI与PPI数据来考察两者之间的传导关系,发现:无论是利用长期和短期数据分析,CPI与PPI都互为彼此的格兰杰原因。杨子晖等采用非线性格兰杰因果检验的方法对多个国家20世纪90年代至2011年问CPI与PPI的传导关系进行检验,发现中国等国家存在PPI向CPI的非线性传导。苏阳等研究中国PPI与CPI的非对称Granger因果关系,得出整体上CPI与PPI互为Granger因果关系。文献也做出相应的研究来验证CPI与PPI之间的关系。非对称结果显示:CPI正冲击与PPI正冲击以及从PPI正冲击到CPI负冲击的方向上,不存在任何Granger因果关系。
从上述的文献中可以看出,由于中国经济体中的经济与金融在不断的提速,对CPI与PPI的研究可能会随着样本区间的延伸而变得不稳定,从而会使研究结果变得无意义。鉴于此,本文选用了国家统计局1996年10月-2019年2月的数据,通过构建VAR模型来研究近年来我国CPI与PPI之间的动态变动关系,为我国的宏观经济调控提供参考。
1 实证分析
1.1数据选取与检验
选取国家统计局公布1996年10月-2019年2月月度同比数据,共269个观测值。从统计分析结果中可以看出:CPI的均值和标准差分别为101.98和2.20,PPI的均值和标准差分别为101.00和4.20,CPI均值大于PPI,但是,PPI的波动明显大于CPI(见表1)。图1是CPI与PPI时序图,从图1可以看出,CPI与PPI走势上基本保持一致,且具备相同的波动周期,这说明CPI与PPI之间具备一定的联系。同时,二者变动的时点和方向不一致,即峰值和谷点不在同一时间,意味着两者之间的联系具有一定的时滞性。
1.1.1纯随机性检验
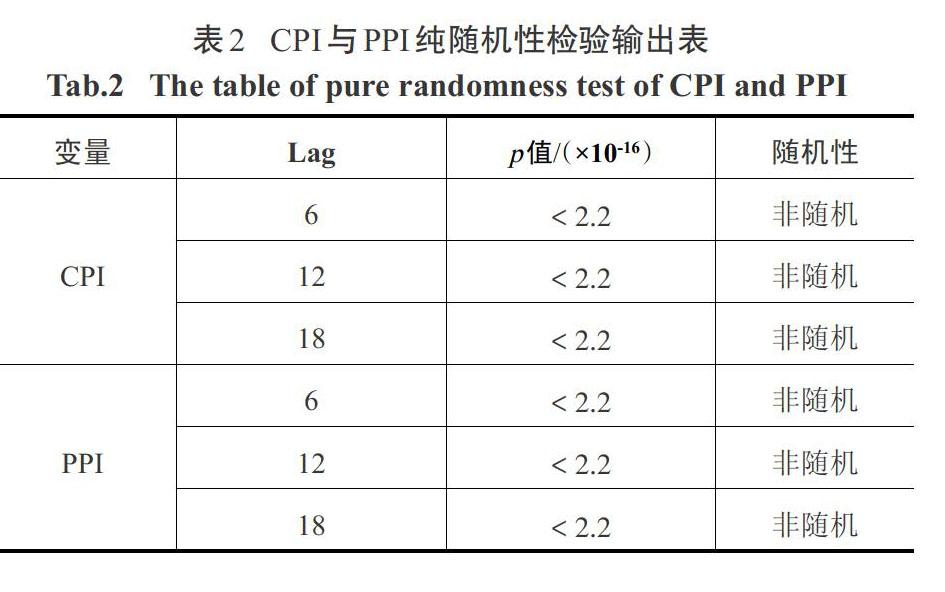
探索CPI与PPI之间模型关系之前,需要对两个序列进行纯随机性检验,观察CPI与PPI两序列是否有研究必要性。
根据表2结果显示,在纯随机检验中,序列{CPI}与{PPI}检验结果显示不能拒绝原假设,故接受原假设,认为{CPI}与{PPI}的波动与具备一定的规律,有一定的研究价值。
1.1.2平稳性检验
在对CPI与PPI建立模型之前,需要根据数据的类型选择合适的模型进行建模,模型的选择规则如下:
1)CPI与PPI均平稳:VAR模型;
2)CPI与PPI非平稳但协整:VEC模型;
3)CPI与PPI均非平稳且不协整:差分形式的VAR模型。
根据以上规则,如果对CPI与PPI建立模型,首先需要对待检验序列进行平稳性检验。一般检验AR(1)过程是否平稳采用DF检验,但为了使DF检验能更加广泛的应用在AR(p)过程的平稳性检验中,研究者对DF检验进行了修正,得到增广DF检验(Audmented Dickey-Fuller),简记为ADF检验。
检验CPI与PPI的平稳性,需检验特征根是否在单位圆内。检验的原假设是至少出现一个单位根,若ADF检验拒绝原假设,则时间序列平稳,反之则非平稳。
CPIt=φ1CPIt-1+…+φpCPIt-p+εt(1)
PPIt=φ1PPIt-1+…+φpPPIt-p+εt(1)
式(1)、式(2)为两个P阶自回归模型,简称为AR(p)模型,其中φ=(φ1,φ2,…,φt-p)T是AR(p)模型的自回归系数,{εt}为白噪音序列,t表示当期,取值范围t=1,2,…,p。
式(1)、式(2)中的εt代表除去CPI与PPI之外的所有因素。确定模型之后对εt进行纯随机性检验,发现εt序列为随机序列,表明除CPI与PPI之外的因素对当期的CPI或PPI的预测结果无影响,即可认为模型结果分析具备确定性,有一定参考价值。
该序列的特征方程可以用下式来计算。
λp一φ1λp-1一…一φp=0(3)
如果式(3)的所有的特征根都在单位圆内,即|λi|<1,i=1,2,…,p,则表示{CPIt}或{PPIt}平稳。
在5%显著水平下对CPI与PPI的ADF检验结果如表3所示。
表3的ADF检验结果显示:在5%的显著水平下对CPI序列进行1-10阶的检验,检验的p值均小于0.05,认为CPI不存在单位根,是平稳序列,从而拒绝原假设。同理,PPI的ADF检验结果显示,PPI序列不存在单位根,为平稳序列,拒绝原假设。
平稳性检验结果确定CPI与PPI均为平稳序列,因此,可以采用向量自回归(VAR)模型来探讨CPI与PPI之问动态关系,无需后续协整检验与差分操作。
1.2VAR模型的建立
VAR模型的建立要求目标序列是平稳的,经检验CPI与PPI为平稳序列,因此可以直接建立VAR模型来研究两者之间的动态关系。首先,使用R软件,调整R方最大以及AIC(Akaike Information Criterion)信息准则最小来综合确定模型的最佳滞后阶数。综合二者结果,最终确定VAR模型滞后阶数为2阶。
AIC=-2ln(L)+2K其中,L——模型最大似然函数,K——模型变量个数。模型对比如表4所示。
由表4对比可以看出,当最大滞后期数选择为3、4阶时,最佳输出模型依旧为2阶模型,因此建立模型为:
图2为回归的拟合图,图2(a)为CPI拟合图,图2(b)为PPI拟合图,根据VAR(2)虚线部分为拟合线与原序列运动趋势几乎吻合,因此,模型具备良好的解释与预测作用。
两个方程的调整R方分别为0.9288和0.9783,说明模型的拟合效果非常好。得到的VAR模型的估计后,需要检验模型的稳定性,采用稳定性检验的方法,检验输出图如图3所示,结果显示在两倍的标准差之内,即两个VAR(2)模型中的εt波动范围都在2倍标准差之内,除CPI与PPI之外的所有因素对VAR(2)模型都没有影响,因此VAR模型稳定,可以用于预测分析。
1.3格兰杰因果检验
格兰杰因果检验要求被检序列是平稳的,因此,可以对CPI和PPI进行格兰杰因果关系检验,但滞后期的选取很重要,随意的选取直接影响检验的结果。本文采用基于VAR模型的格兰杰因果检验,滞后期由AIC值最小确定为2期,表5给出了基于VAR(2)的格兰杰因果检验结果。从表5中看出,在0.05%的显著性水平下,PPI是CPI的格兰杰原因,同时CPI也是PPI的格兰杰原因,即表明CPI和PPI之间互为因果关系。
1.4基于VAR模型的脉冲响应函数分析
因为VAR模型不是一种理论模型,所以分析VAR模型时,一股采用脉冲响应函数分析。脉冲响应函数反映的是给VAR模型的误差项上加上一个单位标准差大小的新信息冲击时,对内生变量的当前值和未来值所带来的影响。脉冲响应函数使用的前提是VAR模型的稳定性通过检验,因为只有稳定的系统模型,脉冲响应函数的结果才具有参考价值。
在图4中列出了4个图,每一个小图的横坐标代表冲击作用之后期长度,纵坐标表示内生变量对VAR模型误差的一个单位标准差大小的冲击的响应程度,实线表示脉冲函数曲线,虚线表示正负两倍标准差偏离带,图4(a)、图4(c)为当给CPI一个标准冲击之后,CPI与PPI的给出的响应,图4(b)、图4(d)为当给PPI一个标准大小冲击时,CPI与PPI对冲击的响应情况。
1)上游价格指数传导至下游价格指数分析,即CPI受到PPI以及自身一个标准差的随机信息的冲击的响应情况。从图4(a)中可以看出,当给本期CPI一个正的冲击之后,发现CPI本身立马就给出了一个较强的反应,第2个月达到最大值57.95%,之后一直缓慢的下降,直到滞后期为第50个月时趋于平稳,且是一直都在2%之上。在图4(b)中可以看出,当给VAR(2)模型中的PPI一个正的冲击时,CPI在第1个月没有立即给出反应,从第2个月开始会有缓慢的增长,在第6个月时最大达到19.78%,然后影响缓慢减少,在第27个月时,反应稳定在2%。这说明PPI的变动会有正向带动CPI的变化,上游价格的变化会影响下游价格的变化,但是PPI对CPI影响滞后期数没有CPI对自身长,最大影响也小于CPI对自身冲击,因此要解决CPI的下降,重点应该着眼于CPI的变化。
2)下游价格指数反馈给上游价格指数分析,即PPl分别受到CPI及自身一个标准差随机信息的冲击的响应情况。从图4(c)中可以看出,PPI对来自于CPI的冲击在第1个月就给出了正向的反应,在2-6个月持续大幅度增长至最大值65.93%,之后便缓慢下降并趋于平稳;同理在图4(d)中,PPI对自身给的一个标准差冲击在第1个月马上给出正向反应并在第5个月达到131.18%,随后影响逐渐减弱,并振荡趋零。说明下游价格对上游价格有很好的反馈作用,随着时间推移反馈影响会增加,但当时滞超过半年,这种正向影响会逐渐消失;同理,PPI对自身扰动变化十分敏感,这种正向影响随时间推移也会逐渐消失。因此,要解决PPI的下降,CPI和PPI的变动都不可忽视,但PPI对变化的应非常敏感,要重点关注。
1.5基于VAR模型的方差分解分析
基于VAR模型还可以对每一个内生变量进行方差分解分析,利用方差分解分析可以量化结构冲击对各自内生变量变化的贡献度,进而分析各自结构冲击的重要性。在脉冲响应分析中,CPI与PPI之间相互都有正向的影响,但是这种影响相比自身的影响小的多。接下来可以利用方差来了解各因素相对冲击的大小。根据表6输出结果可以看出CPI的变动受自身的影响较大,在预测第1期的时候,CPI的预测方差完全由自身引起,之后CPI的变动逐渐受PPI的影响,到第10期时90%由CPI引起,10%由PPI引起。随着时间的推移,CPI预测方差中由自身冲击引起的变化也稳定在90%。在表6的PPI方差分解结果中,第1期预测方差CPI与PPI共同参与扰动,随着时间的推移PPI对自身扰动所引起的变化逐渐稳定占80%,CPI贡献率占20%。所以CPI和PPI的變动大都是由自身引起的,CPI有助于解释PPI的变化,但是PPI对CPI的解释作用较小。
2结论
本文根据我国1996年10月-2019年2月的CPI与PPI的月度同比数据,建立VAR模型,通过格兰杰因果关系检验、脉冲响应和方差分解结果进行分析,得到主要结论如下:1)CPI与PPI互为因果关系;2)通过脉冲响应函数分析,CPI与PPI在受到自身的冲击影响较大,而且二者对自身都是有正向的影响。CPI与PPI之间也有正向的作用,但是由下游价格指数反映到上游价格指数的作用较强,从上游价格指数到下游价格指数的冲击较缓且小,而且这种反映从第2个月才开始;3)通过方差分解分析CPI的变动90%由自身引起,10%由PPI引起,PPI的变动80%由自身引起,20%由CPI引起,所以在研究CPI与PPI的变动问题时,重点关注自身变动,同时注意相互影响。
