赋形旋转抛物面天线母线自适应分段拟合

汪文琪 李宗春 程志峰 张冠宇

(1 中国人民解放军战略支援部队信息工程大学地理空间信息学院郑州450052)

(2 中国电子科技集团第五十四研究所石家庄050081)

1 引言

随着近代电磁学和无线电技术的发展, 反射面天线作为通信、广播、雷达、制导和射电天文等领域的关键设备得到了广泛的应用[1].天线反射面种类繁多, 本文主要关注旋转抛物面天线.标准抛物面天线由抛物线绕焦轴旋转而成, 设计原理简单, 但标准抛物面天线对口径的均匀照射与边缘的能量漏溢存在矛盾, 限制了天线效率的提高, 由此通过修改反射面形状提升天线效率的赋形反射面天线应运而生[2].天线的面型精度是衡量、评价天线质量的重要指标, 它不仅直接影响天线的口面效率, 决定天线可工作的最短波长, 还影响天线方向图的主瓣宽度和旁瓣结构[3].旋转抛物面天线解析方程通过母线的旋转得到, 是评价反射面面型精度的基础.在处理反射面测量数据、评价面型精度中, 文献[3–4]对于旋转抛物面天线测量数据处理和面型精度评价的方法有较为详细的介绍; 另外, 文献[5]分别对比了以轴向偏差、径向偏差、法向偏差和焦距偏差为最小量的4种拟合原则下反射面的拟合情况; 文献[6–7]则以半光程差为最小量对反射面进行拟合.天线的理论设计反射面利用母线设计方程表示, 通过实际反射面与设计反射面的比对可以分析反射面的变形情况, 进而调整反射面的形状和位置实现对变形的补偿, 主反射面调整一般用于含有主动面系统的大型天线, 如国内的中国科学院上海天文台65 m射电望远镜[8–9], 国外的GBT (Green Bank Telescope)望远镜[10]、LMT (Large Millimeter Telescope)望远镜[11]和SRT (Sardinia Radio Telescope)望远镜[12]等; 另一方面, 通过调整副反射面或馈源位置对变形进行补偿更适用于一般的天线, 文献[13–15]给出了一种通过调整副面位置实时补偿赋形卡式天线主面变形的方法; 文献[16]通过拟合的方法调整馈源的位置和指向实现补偿.由此可见, 获取旋转抛物面天线解析方程在处理反射面相关问题时十分必要.

标准抛物面天线的解析方程直接由母线的方程旋转得到, 而对于赋形反射面天线来说, 其理论数学模型复杂, 通常用一组离散点表示[17].为了实现赋形反射面测量数据的处理和面型精度的评定, 需要对母线离散点数据进行拟合.目前, 针对赋形反射面母线离散点数据拟合常用的方法主要有两种: 一种是直接利用多项式对离散点数据进行整体拟合, 如文献[18]中利用19阶多项式对口径13 m以内的天线母线数据进行了拟合, 这种方法不需要考虑离散点数据的特点, 拟合思路简单直接, 对于拟合点来说能够达到较高精度, 但多项式阶数较高, 拟合计算工作量大, 而且利用高阶多项式拟合曲线容易振荡,导致拟合结果在边缘处不稳定; 另一种是通过等间隔分段的方式利用低阶多项式对母线数据进行拟合, 文献[13–16]均采用了这种方法, 等间隔分段拟合在一定程度上可以降低高阶多项式拟合的不稳定性, 但这种分段方式具有一定的盲目性, 容易导致分段数过多,造成拟合参数量过大、母线拟合光滑性差的问题.

针对以上方法在赋形反射面母线拟合中存在的问题, 本文提出了一种基于母线拟合残差分布的自适应分段拟合方法, 这种母线自适应分段拟合的方法包括两步—初始整体拟合和分段拟合.初始整体拟合为分段拟合确定了残差的分布情况, 依据母线拟合残差分布的特点, 通过设置一定的阈值找出拟合残差不同分布的节点; 分段拟合参照初始整体拟合的结果进行拟合, 利用节点划分残差的范围, 以此为依据对母线离散点数据进行分段, 再分别采用低阶多项式进行拟合.

2 传统母线拟合方法

2.1 多项式整体拟合

赋形反射面母线通过离散点的坐标数据表示, 多项式整体拟合方法[18]直接利用多项式对离散点数据进行拟合以获取母线的方程, 如(1)式所示:

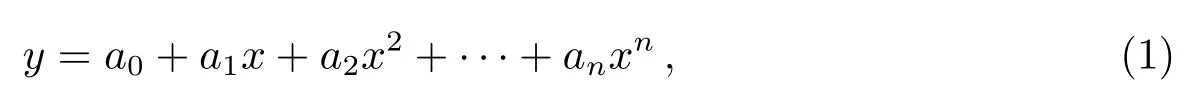
式中, a0,a1,a2,··· ,an为多项式系数, 也就是母线拟合参数, n为多项式阶数.

拟合时, 首先利用母线设计时给出的m个离散点数据列出m个误差方程, 如(2)式所示:

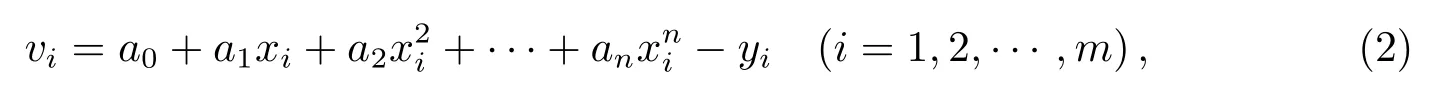
式中, (xi,yi)为母线离散点坐标, vi为yi的改正数, 也就是残差; 然后利用最小二乘原理即可求得母线参数a0,a1,a2,··· ,an.在拟合过程中, 按照由小到大的顺序依次增大多项式的阶数, 直到多项式拟合的精度满足母线拟合要求.为了使拟合结果达到精度要求, 所采用的多项式阶数往往较高.

2.2 等间隔分段拟合

将表示理论母线的一组离散点数据进行分段, 分别用低阶多项式对各段进行拟合[13–16], 以此来得到赋形反射面的母线方程.赋形反射面母线的离散点数据为m个, 共划分k段, 令前k–1段的离散点个数相同.在拟合过程中应该保证相邻分段函数的连续性,为此相邻分段间应具有一个公共点, 在公共点处两个函数的函数值相同.公共点处函数值相同相当于在利用最小二乘原理进行拟合时增加了限制条件, 对于这种含有限制条件的拟合, 本文采用具有约束条件的参数平差[19]予以实现.按照这种划分方法相当于每两段之间增加了一个离散点, 则母线总的离散点个数增加k–1个, 前k–1段上每段包含离散点的数目为

式中, [·]表示按四舍五入取整.

第k段离散点数为mk=m+k −1 −mk−1(k −1).利用分段方法对赋形反射面拟合时宜采用循环迭代的方式, 逐次增加分段数直至满足母线拟合的精度要求.随着分段数目的增加, 母线拟合的参数增多, 拟合处理过程中计算复杂程度也随之提升.

3 自适应分段拟合

前文已经提及, 传统的两种母线拟合方法均存在一定的不足之处.本文结合这两种方法的特点, 在此基础上提出了一种自适应分段拟合的方法.自适应分段拟合方法由初始整体拟合和分段拟合两部分组成, 不同于等间隔分段中直接将母线数据按长度均匀分段的方法, 该方法先进行初始整体拟合, 然后参照初始整体拟合结果残差的分布特点自适应地选择分段的节点, 对母线离散点数据进行分段拟合.具体流程如下:

(1)选择某一低阶多项式对母线数据进行初始整体拟合, 由(2)式计算各拟合点的vi,并取其绝对值|vi|.

(2)设置一定的阈值t, 当|vi| t时将该点标记为0, 否则标记为1, 如下所示, 由此得到拟合残差绝对值的0–1分布:

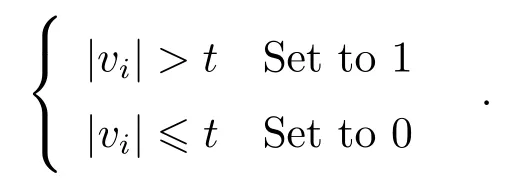
(3)根据拟合残差的0-1分布状态对母线数据进行分段, 将残差相同的区域分为一段,如图1所示, 图1 (a)中l1部分全为0, l2部分全为1, 由此可将母线数据分为2段, 同理图1(b)中数据可分为3段; 同时, 设定分段最低要求点数为d, 当段中离散点个数小于d时, 不满足分段最低点数要求, 将此段数据与相邻两段数据合并成一段.不满足分段最低点数要求的情况只有两种, 分别如图2 (a)和图2 (b)所示, 图2 (a)和图2 (b)中的l2段离散点个数小于d, 在拟合过程中直接将l2段与相邻两段数据合为一段.

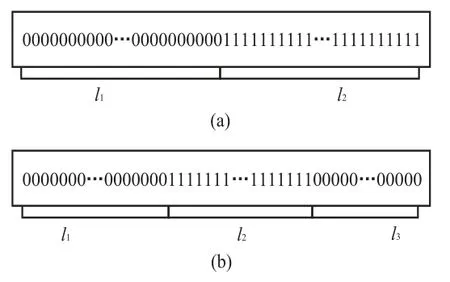
图1 母线拟合残差0–1分布状态Fig.1 The 0–1 residual error distribution of generatrix fitting

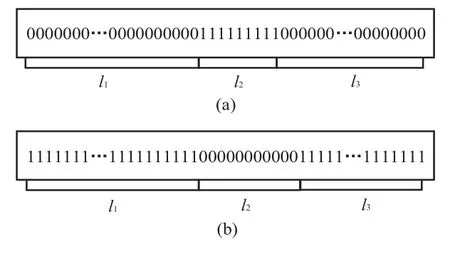
图2 母线拟合残差0–1分布的特殊情况Fig.2 The special case of 0–1 residual error distribution of generatrix fitting

(4)采用低阶多项式分段对母线数据进行拟合, 相邻两段之间采用公共点连接, 即在公共点处相邻两段母线拟合函数的函数值相同, 以确保母线拟合结果的连续性.

4 实例计算

母线拟合结果一般以最大逼近误差(Maximum Approximate Error, MAE)作为评价标准, MAE即为拟合结果中残差绝对值的最大值.工程测量中通常采用可忽略不计原则[20], 即当一种误差等于或小于另一种误差的1/3时, 这一误差对总限差的影响可忽略不计.根据天线反射面的实际测量精度和工艺水平, 本算例设定测量误差σ =0.050 mm,取MAE为σ/3=0.016 mm, 以此作为母线拟合结果的限定条件.

4.1 3种方法拟合结果

本文以某13 m赋形反射面天线母线数据为例对3种方法的拟合结果进行检验, 该母线数据由765个离散点组成.由于离散点坐标范围变化较大, 为了防止拟合过程中求解法方程病态, 可以先将坐标数据进行标准化处理, 常见的标准化方法有Min-Max标准化、Z-score标准化和小数定标标准化等.本文选择Z-score标准化方法[21]分别将离散点x坐标和y坐标标准化, 标准化公式如下

将母线坐标数据按照(4)式标准化之后, 对标准化数据进行拟合, 最后再把拟合结果转换回原始数据.

4.1.1 多项式整体拟合结果

直接利用多项式对母线数据进行整体拟合, 逐次增加多项式的阶数, 直到母线拟合结果满足限定条件.在多项式从低阶到高阶变化过程中, 分别统计出不同阶次多项式拟合结果的MAE和拟合残差的均方根值(Root Mean Square, RMS), 其中均方根公式为

拟合结果见表1, 从中可以看出, 母线拟合的RMS随多项式阶数的增加逐渐减小, 这表明对于离散点数据, 高阶多项式拟合的整体效果优于低阶多项式; MAE随多项式阶数的增加没有单调下降, 而是略有波动, 但总体呈现出减小的趋势, 并在阶数达到13阶时满足母线拟合的限定条件.

表1 不同阶次多项式拟合结果Table 1 Fitting results of polynomials with different orders

4.1.2 等间隔分段拟合结果

按照等间隔的方式对母线离散点数据进行分段, 每段均采用3阶多项式进行拟合.统计出不同分段下母线拟合结果的MAE和RMS, 结果如表2所示.从中可以看出, 随着分段数的增加, 母线拟合的RMS逐渐减小, 说明分段越多, 母线拟合的整体效果越好;MAE与不同阶次多项式拟合结果类似, 局部略有波动, 总体呈现出下降的趋势, 并在分段数为7段时达到了母线拟合的精度要求.

表2 等间隔分段拟合结果Table 2 The result of equal-interval piecewise fitting

4.1.3 自适应分段拟合结果

按照自适应分段拟合的方法逐步进行:

(1)选择3阶多项式对母线数据进行初始整体拟合, 计算出各点拟合残差的绝对值,结果如图3所示.

(2)母线拟合MAE的限定值为0.016 mm, 可将阈值设置为MAE限定值的1/n, 使得拟合方法能够根据限定条件自动设置阈值.因此t = 0.0053 mm, 由此得到的拟合残差0–1分布结果如图4所示.

(3)当段内点数过少时不适合单独进行拟合, 需要确定母线分段最低要求点数d.取一定比例s的母线长度作为单位母线长, 因为母线离散点分布均匀, 所以单位母线长所对应的离散点数即为分段最低要求点数d, 同时, 确定了单位母线长也意味着确定了母线所能分段的最大数目(母线长/单位母线长).为了方便不同口径反射面天线的选取, s取值设置成一定的范围1%–5%, 口径越大的天线对应的s越小, 这样所允许的母线最大分段数也越多, 符合现实情况.结合文献[22]中对反射面天线大中小型的分类, 表3分别列出了各类天线所对应的比例s.

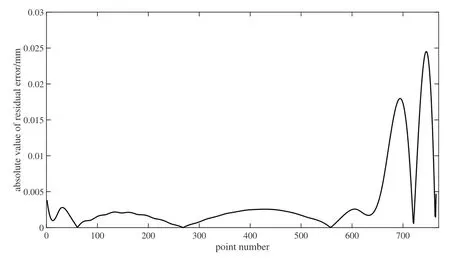
图3 初始整体拟合残差绝对值Fig.3 The absolute value of initial overall fitting residual error

图4 初始整体拟合残差0–1分布Fig.4 The 0–1 distribution of initial overall fitting residual error

从表3中可以看出, 本例中的天线所对应的s为4%, 则d = 765s = 30.6, 将d取为30.对于图4中拟合残差的分布, l3段和l5段中离散点个数均小于d, 将这两段数据与相邻段合并处理, 合并之后的残差分布如图5所示.其中, 658号点是残差分布变化的节点, 由此可将母线数据分为两段, 前658个点作为第1段, 后107个点作为第2段, 其中, 658号点作为两段的公共点.

表3 不同口径天线对应的比例sTable 3 The ratio s of antennas with different apertures

图5 合并后残差的0–1分布Fig.5 The 0–1 distribution of residual error after mergence

(4)分别采用3阶多项式对两段数据进行拟合, 计算出拟合结果的MAE和RMS.

经过上述流程的拟合计算, 母线数据总体分段数为2段, 拟合结果的MAE为0.014 mm, 满足拟合精度要求, 具体结果见表4.

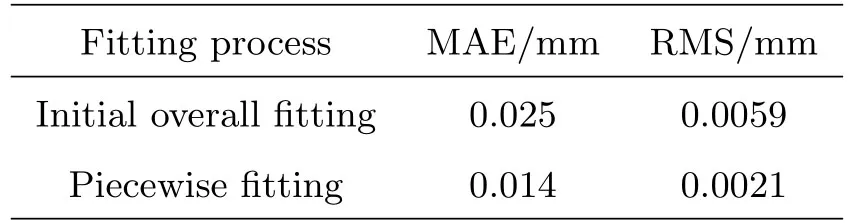
表4 自适应分段拟合结果Table 4 The result of adaptive piecewise fitting

4.1.4 结果分析

3种方法拟合得到的参数数目如表5所示, 从中可以看出, 在满足母线拟合同一精度要求的情况下, 3种方法中本文提出的自适应分段拟合方法所用到的参数最少, 仅用到了8个, 简化了母线的表达形式, 方便了后续计算.另外, 自适应分段拟合第1段中包含了658个离散点, 而与之范围相近的离散点数据利用等间隔分段拟合方法却分了6段进行拟合, 大大增加了拟合参数的数目, 由此可以看出等间隔分段拟合方法的盲目性; 同时,在拟合过程中只保证了拟合曲线的连续性, 各连接点左右两侧导数并不相同, 这会影响到拟合结果的光滑性; 随着分段数的增加, 连接点数目增多, 母线拟合结果的整体光滑性逐渐变差.

3种方法的母线拟合结果如图6所示, 两端点中间的母线部分3者相近, 基本重合; 在拟合边界部分, 多项式整体拟合曲线的斜率有一个明显增大的趋势, 反映了高阶多项式拟合的不稳定性, 这会给后续的天线反射面拟合带来不利的影响.

综合以上内容可以发现, 母线拟合的3种方法各有特点:

(1)多项式整体拟合的方法, 拟合过程简单直接, 但往往导致拟合多项式阶次过高、计算量大, 且高阶多项式在边缘处拟合结果不稳定;

(2)等间隔分段拟合, 拟合多项式采用低阶次多项式, 计算简单但分段不合理, 循环次数多, 导致拟合结果分段数较多、拟合参数量大, 而且较多的分段会造成拟合曲线不光滑的现象;

(3)自适应分段拟合的方法兼顾了2者的优点, 初始整体拟合确定残差的分布, 分段拟合参照残差的特点进行分段, 分段合理、操作简便, 能够以较少的参数满足母线拟合的要求.

表5 不同方法拟合参数的数目Table 5 The number of fitting parameters in different methods

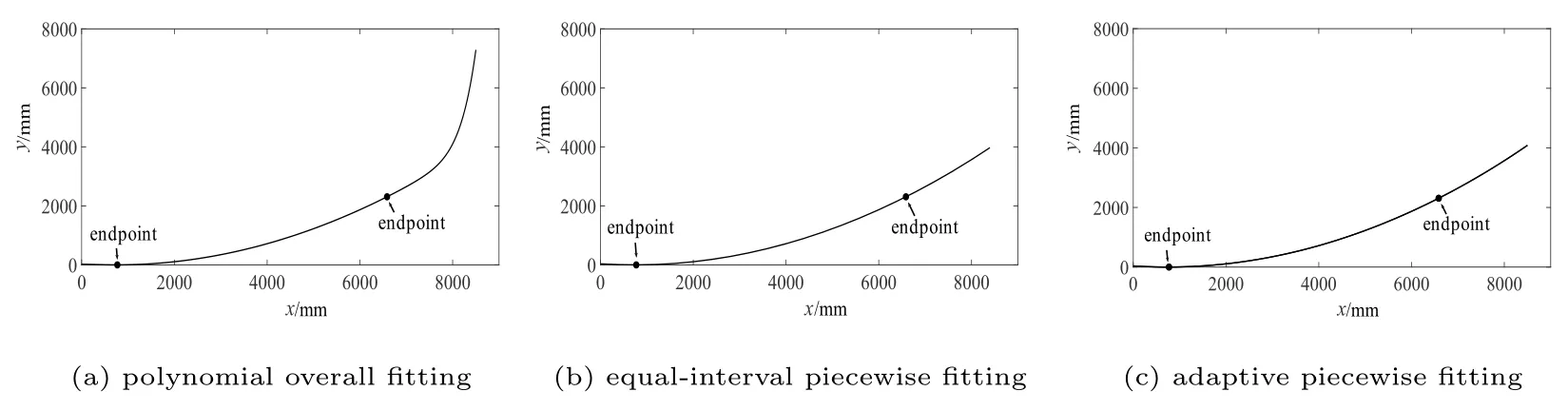
图6 3种方法的母线拟合结果Fig.6 Generatrix fitting results of three methods

4.2 方法扩展

为了进一步提升自适应分段拟合方法的拟合效果, 本文继续在多项式阶次和公共点限制条件两个方面进行探究.

4.2.1 拟合多项式的选择

4.1.3节中利用了3阶多项式对母线数据进行了分段拟合, 为了进一步验证多项式阶次不同对母线拟合结果的影响, 这里采用了2阶、4阶和5阶多项式对母线离散点数据进行拟合, 拟合结果见表6.从中可以看出, 随着多项式阶数的增加, 自适应分段拟合效果有了明显的提升; 但当拟合精度达到一定程度之后, 再增加多项式的阶数没有明显的意义, 这一点可以从4阶多项式和5阶多项式拟合结果的对比中看出.因此, 在符合母线拟合精度的条件下, 拟合多项式宜选择低阶次; 当拟合结果不能满足母线拟合要求时, 适当增加多项式阶数可以改善拟合的结果.

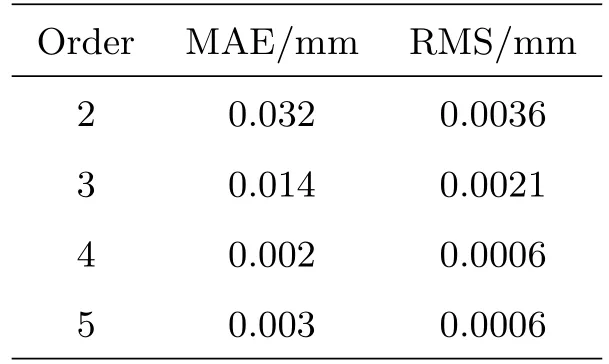
表6 不同阶次多项式母线拟合结果Table 6 Generatrix fitting results of polynomials with different orders

4.2.2 公共点限制条件

4.1.3节中为了保证母线拟合的连续性, 相邻两段母线数据中采用了公共点进行连接.相邻两段母线拟合函数在公共点处的函数值相同确保了母线拟合的连续性, 但公共点处的光滑性没能得到保证.母线拟合的光滑性与公共点两端的导数有关, 两端相等导数的阶次越高, 母线拟合结果越光滑.因此, 本文以4次多项式拟合为例, 逐次增加公共点处导数相等的限制条件.

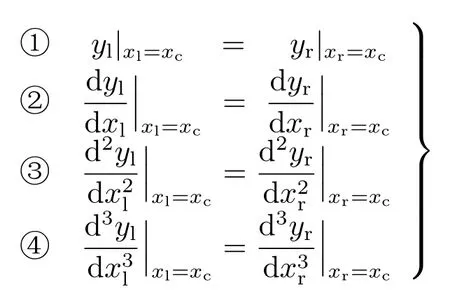
其中, ①条件表示公共点(xc,yc)处左右两端拟合函数的函数值相同, ②③④条件分别表示公共点处左右两侧的1阶导数、2阶导数和3阶导数相同.

表7为不同阶次多项式母线拟合结果.从表7中可以看出, 随着公共点处限制条件的增加, 拟合得到的MAE和RMS增大, 说明拟合精度变差.分析其原因, 公共点处限制条件越多, 相邻两段之间的联系越为密切, 不利于各自分段的拟合, 从而导致拟合精度的下降.因此, 可以在保证满足精度要求的前提下, 适当增加公共点处的限制条件, 以提升母线拟合结果的光滑性.

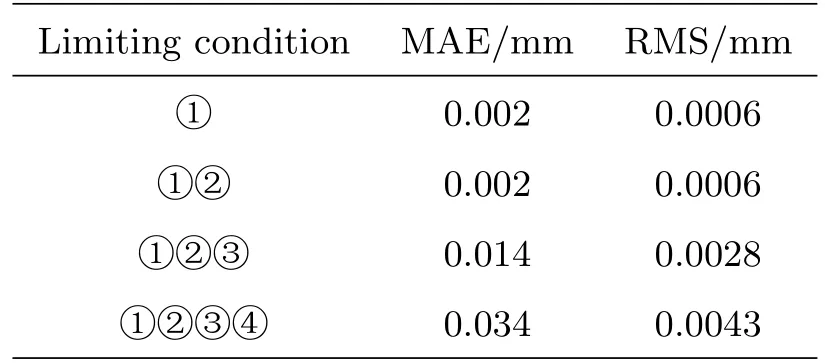
表7 不同公共点限制条件的拟合结果Table 7 Fitting results of constraint conditions with different common points

5 总结

赋形反射面母线传统拟合方法存在不足之处: 多项式整体拟合的方法阶次高、计算量大, 拟合结果不稳定; 等间隔分段拟合方法分段不合理、分段数过多, 导致拟合参数多、拟合曲线不光滑.本文提出的自适应分段拟合方法, 以初始整体拟合结果的残差分布为基础进行分段, 分段方式合理, 采用低阶多项式逐段进行拟合, 计算简单, 能够以较少的参数满足母线拟合的要求, 方便了后续面型精度的评价.相比于其他方法, 本文方法更适合于赋形反射面天线母线的拟合.同时, 在满足拟合精度的基础上, 选择恰当的拟合多项式、增加公共点限制条件, 可以进一步提升母线拟合结果的质量.