ESO 113-G010的一对准周期振荡信号∗
2020-02-12颜景志刘庆忠
张 鹏 颜景志 刘庆忠
(1 中国科学院紫金山天文台暗物质与空间天文重点实验室南京210033)
(2 中国科学院大学北京100049)
(3 中国科学技术大学空间科学与天文学院合肥230026)
1 引言
活动星系核(Active Galactic Nuclei, AGN)是一类中央核区活动性很强的河外星系, 能谱特征表明其光度并不是由恒星活动产生的.一般我们认为其中心存在超大质量黑洞(Black Holes, BHs), 黑洞周围存在吸积盘.窄线赛弗特星系(Narrow-line Seyfert I galaxy, NLS1)是活动星系核中的一种.窄线赛弗特星系的X射线光变曲线中有时会出现准周期振荡(Quasi-Periodic Oscillation, QPO)现象.QPO有两种类型[1]: 低频QPO(Low-frequency QPOs,LFQPO)和高频QPO(High-frequency QPOs,HFQPO).HFQPO有时会呈现两个瞬态QPO信号, 其频率比为1:2[2–3]或2:3[4].
QPO在银河系以及附近星系中的中子星和黑洞双星中相当普遍[1].尽管我们已经发现大量的AGN, 但在AGN中发现QPO是非常罕见的.在NLS1中第1个发现QPO的源是RE J1034+396[5], 有约1 h (3730 s)的准周期信号.此外, QPO在1H 0707-495[2–3],Mrk 766[4], M82 X-1[6]和MCG-06-30-15[7]均有发现.
ESO 113-G010 (红移z = 0.026)是一个著名的源, 它在5.4 keV处存在一条高红移的铁Kα线[8].从赛弗特星系的分类上来说, ESO 113-G010是Seyfert 1.8星系[9], 它的Hβ线宽(半高全宽, FWHM)小于2000 km·s−1.另外, ESO 113-G010的光度具有强烈的变化和软X射线超, 在6.52 keV和6.97 keV处存在两条高斯线[10].
在X射线光变曲线中搜索QPO是非常重要的: AGN的X射线辐射来自吸积盘的内区, 研究QPO性质可以有助于我们研究黑洞和其周围的吸积盘理论.QPO是暂现的, 其起源有多种模型来进行解释, 但并未形成一个统一的理论.此前的观测中曾发现在不同的观测时间出现两个频率不同的QPO信号[4], 或者在同一次观测中的不同时刻出现了两个不同频率的QPO信号[3].研究QPO有利于更好地了解从恒星级黑洞到超大质量黑洞吸积的本质, 同时也是研究黑洞周围强引力场的窗口.
我们对ESO 113-G010的观测数据进行了处理, 以期找到QPO存在的证据.在本文第2节中, 我们将介绍数据分析方法并展示主要结果.讨论和我们的结论在第3节中给出.
2 数据和分析
2.1 数据处理
XMM-Newton X射线望远镜由欧洲航天局于1999年12月10日发射, 搭载3个光子成像相机[11–12](EPIC), 其中包括一个PN探测器和2个MOS探测器, 两个反射光栅光谱仪[13](2RGS)和一个光学监视器(OM).ESO 113-G010被XMM-Newton观测了2次,分别是在2001年5月和2005年11月.在本文中我们使用2005年观测的数据, 观测ID为0301890101, 其曝光时间为103 ks.
数据分析是按照由XMM-Newton科学运营中心提供的科学分析软件(SAS)中的标准程序进行, 版本为15.0.0.首先, 我们通过工具evselect获得观测数据并得到图像.我们选择源位置半径为40的感兴趣区域(ROI)的数据, 其中心位于赤经01:05:16.89和赤纬−58:26:14.81, 能段为0.3–10 keV.要在时间或者计数率上进行过滤, 我们可以使用工具tabgtigen创建辅助的好时间间隔文件(Good Time Interval,GTI).我们在工具evselect中使用参数PATTERN 4来获得高质量的科学数据, 采用的时间bin为100 s.为了消除由背景光子引起的误差, 我们选择了与源区域大小相同的没有任何X射线源的区域作为背景.最后, 使用SAS命令epiclccorr改正仪器因素, 最终得到ESO 113-G010的EPICPN的光变曲线, 见图1.
2.2 光变曲线数据分析
在图1的顶部展示出了ESO 113-G010在0.3–10 keV能段的103 ks连续光变曲线.为了更准确搜寻准周期信号, 我们使用两种最广泛使用的方法分析数据, 分别为Lomb-Scargle周期图(LSP)法[14–16]和加权小波Z变换(Weighted Wavelet Z-transform, WWZ)法[17].在下文中, 我们将简要介绍这些方法.
小波变换作为时间序列中的周期分析方法显示出了很大的优势, 特别是用于检测描述周期性和伪周期性信号的参数(周期、幅度、相位)的时间演变.通过将小波变换作为投影, 我们可以推导出其统计行为并设计适合的变换.通过将其视为加权投影以形成加权小波Z变换, 提高了其检测周期和伪周期信号的能力.在本文中, 我们使用的是Foster在1996年提出的方法: WWZ[17].我们将得到的光变曲线进行WWZ分析, 可以得到在时间和频率上的2维图, 通过2维图, 我们就可以判断该光变曲线是否有周期以及该周期出现的位置.LSP法是Lomb在1976年以及Scargle在1982年提出来的一种寻找周期性信号的方法[14–16].它跟WWZ使用的原理跟方法不同, 其优点是能够用于分析不规则时间序列中的周期性, 其采用χ2统计量来拟合整个数据序列中的正弦波.它减少了不规则采样的影响, 并指出了数据中可能存在的任何周期或准周期, 并且还可以计算它们的显著性.
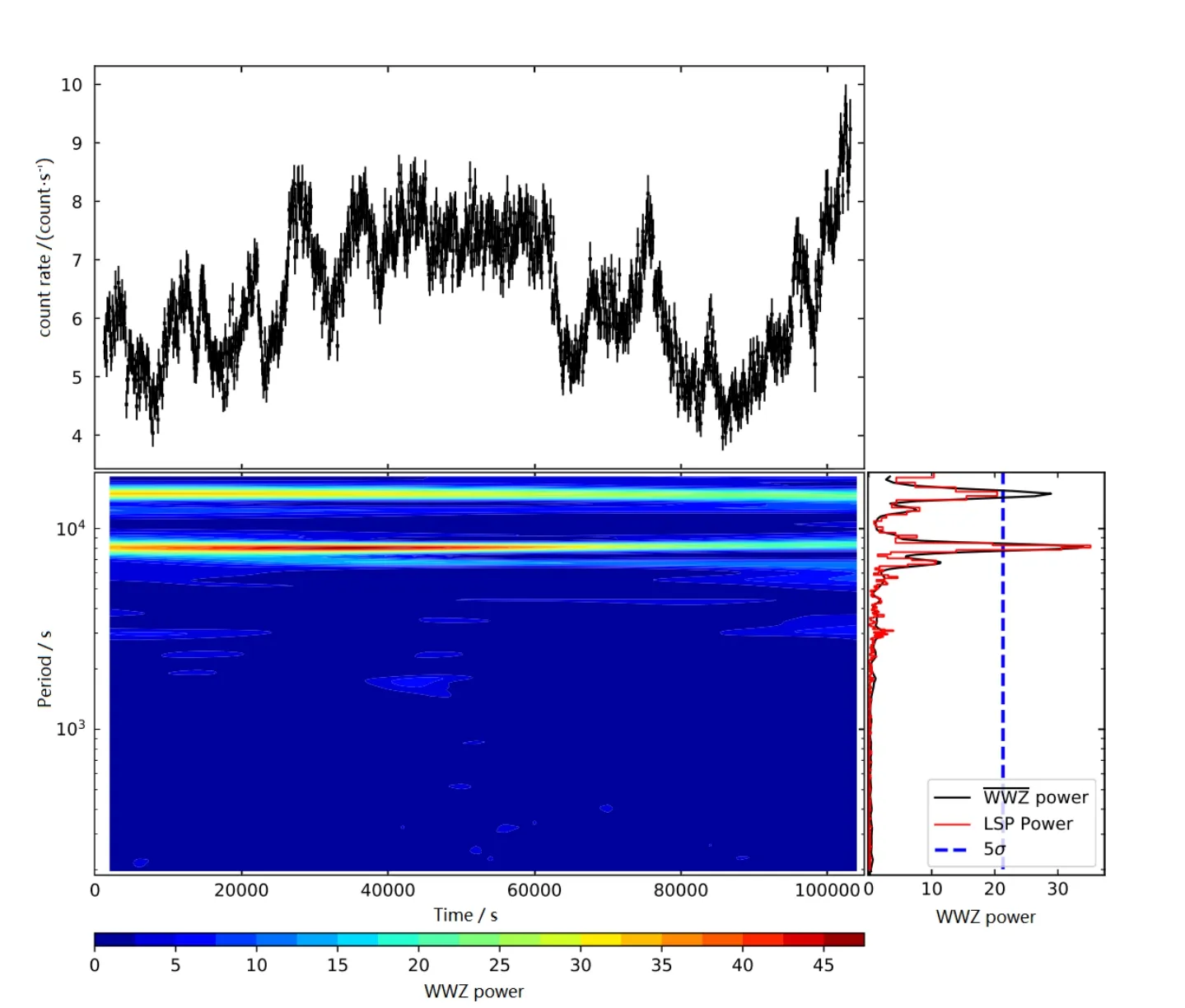
图1 ESO 113-G010的EPIC-PN数据处理结果.图的上半部是ESO 113-G010的EPIC-PN的光变曲线, 下半部的左边是整个光变曲线的WWZ功率谱, 下半部的右边中黑色的曲线是WWZ功率谱按时间平均的结果(), 红色的曲线是LSP法分析的结果.5σ的置信度在图中用蓝色虚线表示了出来.Fig.1 The result of ESO 113-G010 EPIC-PN data processing.The upper panel: XMM-Newton EPIC-PN light-curve of ESO 113-G010.The lower panel: 2D plane contour plot of WWZ power of the whole light-curve.The lower right panel: the red and black solid lines represent LSP power and time-averaged WWZ power(), respectively; the confidence-level of 5σ is shown with a blue dashed line.
WWZ及LSP的结果见图1的下半部.从图中我们可以看到, 用WWZ方法和LSP法同时在1.24 × 10−4Hz (8064.5 s)处发现了一个非常强的峰值(信号1), 而在6.8 × 10−5Hz (14706 s)处存在着一个弱一些的周期性信号(信号2).
我们计算了两个信号是由随机噪声产生的概率(p)[18], 得到它们的概率分别是pprob1.55×10−16(信号1)以及pprob1.05×10−9(信号2), 这些概率代表由随机噪声产生的功率大于或等于功率谱中最大功率的可能性(pm).其计算公式为pprob(p pm) =其中M是光变曲线分bin的个数.然后, 基于采样频率数量(N)校正概率,也即是得到假警报概率FAP=1 −(1 −pprob)N, 这里的采样频率数量N =1530.最后, 我们估计出功率谱的置信度曲线, 如图1右下图所示, 其中蓝色虚线代表5σ置信度水平.我们得到信号1的置信度水平为7.3σ, 信号2的置信度水平为4.8σ.
2.3 能谱分析
为了更准确地研究ESO 113-G010的能谱性质, 我们使用XSPEC (v.12.9.0n)[19]来进行分析.我们采用能段0.3–10 keV的数据, 并参照Mallick等[20]的方法, 使用两种模型来对数据进行拟合.
为了检验软X射线超的起源, 在模型1中(如图2所示)我们使用电离吸积盘的相对论反射模型[21–24]reflionx和宽发射线卷积模型relconv[23]对软X射线超进行建模.在校正银河系吸收(TBabs)后, 我们将0.3–10 keV EPIC-PN平均光谱用相对论反射模型(relconv× reflionx)进行拟合.吸收边界条件为zedge.我们仿照Cackett等[10]的方法添加了两条高斯线(zgauss (1)、zgauss (2)), 为其提供了拟合统计的改进, 拟合结果显示, 高斯线分别位于6.49 keV和7.01 keV.
另外, 在模型2 (如图3所示)中我们还通过使用计算了红移的幂律谱模型(zpowerlw)以及银河系吸收模型(TBabs), 使用Wilms等[25]的横截面和星际介质吸收(Interstellar Medium, ISM)来对我们的EPIC-PN数据进行光谱分析.我们将氢原子柱密度固定在NH= 2.30 ×1020cm−2[26].该模型可以被认为是描述来自源的硬X射线发射的良好基线模型.单独使用吸收幂律模型(TBabs × zpowerlw)拟合, 在软X射线处残差非常大, 揭示了存在低于1 keV的软X射线超, 因此我们使用简单的黑体模型(zbbody)对软X射线超发射进行建模.拟合出来的黑体温度kTBB= 94.9 eV, 这与观测到的NLS1的软超的温度一致[27–28].此外, 我们也加入了两条高斯线(zgauss)的模型[10], 拟合结果显示两条高斯线位于6.52 keV和7.01 keV处.
所有拟合得到的参数都列于表1中.同时, 该表的最后两行列出了模型与原数据之间的拟合程度在90%置信度限制下的卡方以及拟合优度χ2/υ, 两种模型分别为1238.07/1.025和1342.84/1.11, 显示拟合优度都非常高.
3 总结和讨论
在本文中,我们分析了XMM-Newton X射线望远镜对NLS1 ESO 113-G010在2005年的观测数据, 得到了它在2.24 h (1.24 × 10−4Hz)处有一个置信度高达7.3σ的周期性信号.在XMM-Newton的另一次观测数据中, 我们并没有检测到该信号的出现.如同Mrk 766[4], 1H 0707-495[3]那样, 我们认为ESO 113-G010中的QPO信号也是一个暂现的周期性信号.在之前的研究中, 1H 0707-495在同一次观测中不同时刻出现了1:2的两个周期性信号[3], 而Mrk 766则在不同的观测中出现了2:3的周期性信号[4].而在这次的观测中, 我们注意到, 在ESO 113-G010的6.8 × 10−5Hz处也有一个周期性信号, 其置信度约为4.8σ.这两个周期性信号的比例大约为1:2 (1:1.83).
HFQPO的起源尚不清楚, 但是现在人们普遍认为, QPO信号可以通过黑洞周围吸积盘的不稳定性产生, 例如相对论进动模型(RPM)[29], 共振模型(RM)[30], 声学振荡压力支持吸积环的模型(AOM)[31], 吸积盘中的吸积-喷流不稳定性(AEI)[32]以及不同模式下的盘振荡(g模式、c模式、p模式)[33]等引起的.所有这些模型都可以解释双峰QPO的2:3频率比, 这些模型还预测了MBH-fQPO的关系.然而, 只有AEI和p模式可以解释为什么HFQPO仅在非常高的吸积状态下发生[34].在黑洞双星中存在着大量的频率比近似为2:3的高频QPO, 这暗示着它们可能是由某种共同的共振机制引起的[30,35–36].

表1 ESO 113-G010的能谱拟合参数Table 1 The spectral parameters of ESO 113-G010 best-fitting
在RE J1034+396[5], 1H 0707-495[2–3]以及Mrk 766[4]中观测到的QPO被认为是HFQPO[37], ESO 113-G010中出现的QPO, 我们认为它也是一个HFQPO.原因在于他们的能谱形状相似, 其X射线能谱在0.3–1 keV之间有软X射线超, 并且有很高的爱丁顿比率.在MBH-fQPO的关系图中, 显示出了ESO 113-G010同前面的源(其中包括黑洞X射线双星, NLS1)具有一致性[1–2,37–38].如图4所示.在黑洞X射线双星和NLS1中,HFQPO的起源尚不清楚, 我们的结果可为这一研究提供更多信息.
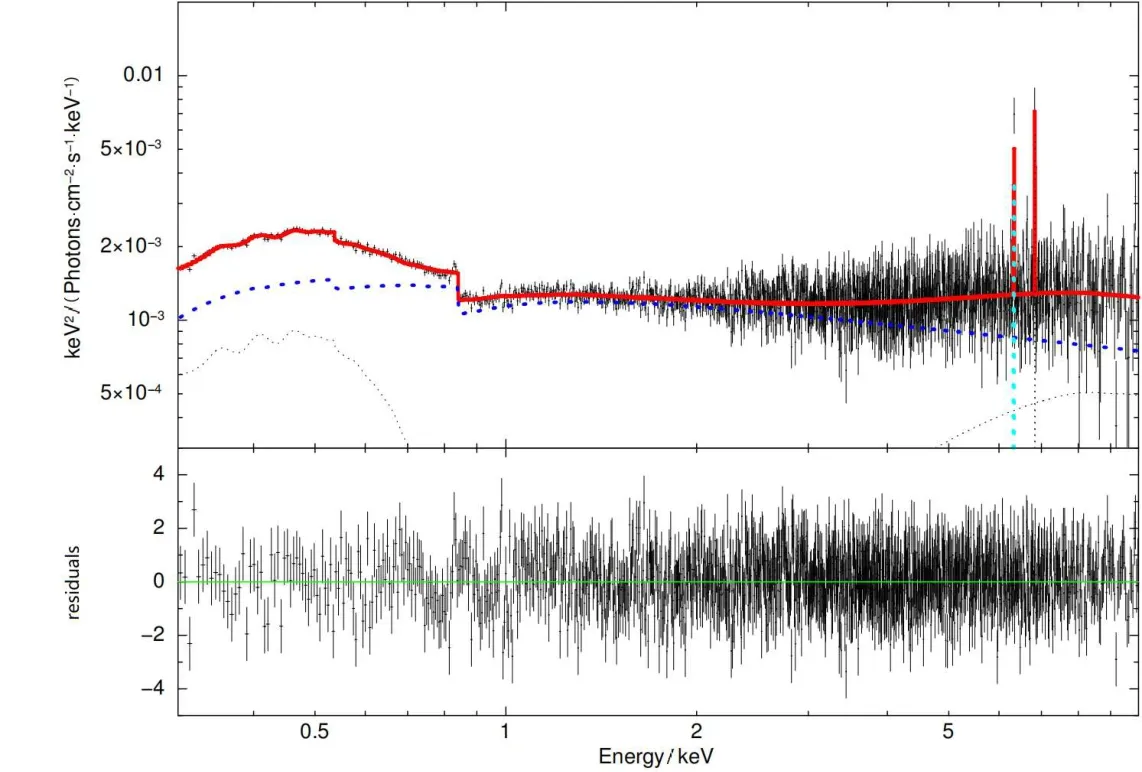
图2 EPIC-PN数据在模型1下的能谱拟合结果, 使用的最佳拟合模型: TBabs × zedge × (zpowerlw + zgauss (1)+ zgauss (2) + relconv × reflionx)以及残差.黑色的线代表EPIC-PN数据, 红色的实线是模型1的拟合曲线, 蓝色、黑色和青色的点线分别为吸收幂律谱模型、反射模型以及两条高斯线.Fig.2 The result of EPIC-PN spectra fitting in Model I.The best-fitting model is TBabs × zedge ×(zpowerlw + zgauss (1) + zgauss (2) + relconv × reflionx) and the residuals.Black line represents the EPIC-PN data, red solid line is the fitting curve of Model I, and blue, black, and cyan dotted lines are respectively the absorbed power-law model, reflection model, and two Gaussian lines.
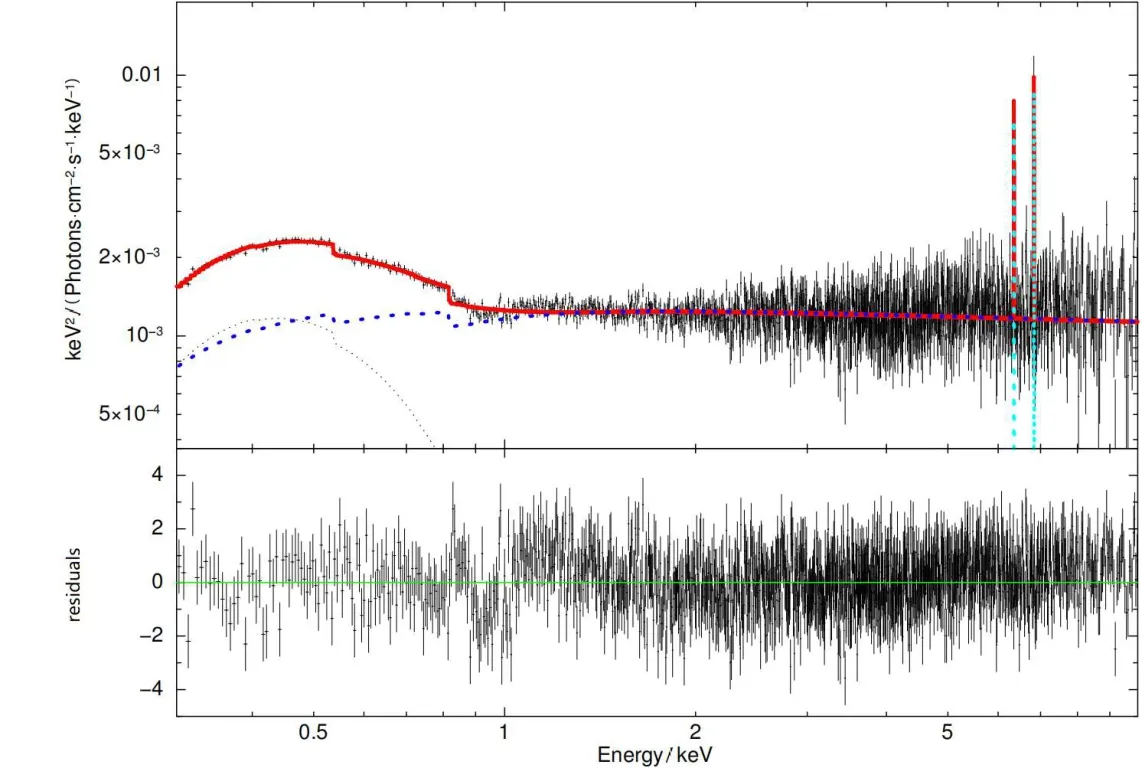
图3 EPIC-PN数据在模型2下的能谱拟合结果, 使用的最佳拟合模型: TBabs × zedge × (zpowerlw + zgauss (1)+ zgauss (2) + zbbody)以及残差.黑色的线代表EPIC-PN数据, 红色的实线是模型2的拟合曲线, 蓝色、黑色和青色的点线分别为吸收幂律谱模型、黑体辐射模型以及两条高斯线.Fig.3 The result of EPIC-PN spectra fitting in Model II.The best-fitting model is TBabs × zedge ×(zpowerlw + zgauss (1) + zgauss (2) + zbbody) and the residuals.Black line represents the EPIC-PN data, red solid line is the fitting curve of Model II, and blue, black, and cyan dotted lines are respectively the absorbed power-law model, Black body radiation model, and two Gaussian lines.
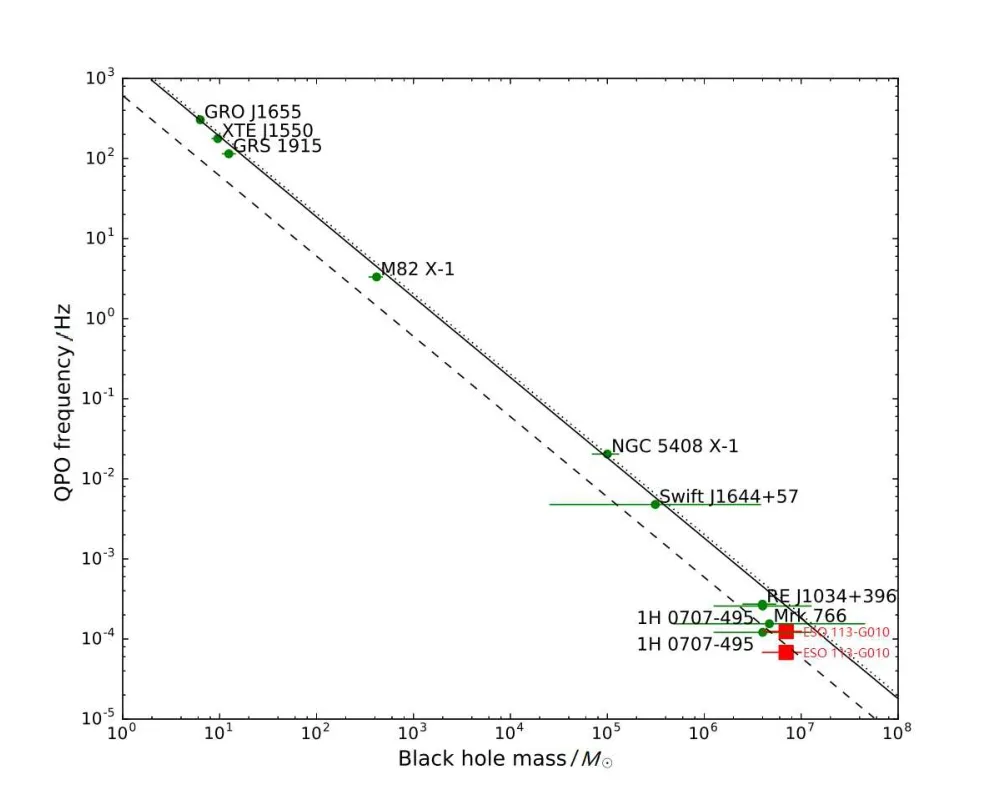
图4 黑洞质量与QPO频率的关系图.图中的深绿色数据点是前人的结果[1–2,30,37–38], 红色实心方框代表着ESO 113-G010的位置, 图中实线代表着来自Remillard等[1]的关系, 虚线代表Kluzniak等[38]提出的2:3的关系.Fig.4 The correlation between BH masses and QPO frequencies[1–2,30,37–38].The events reported in previous works are shown with dark green points and the new QPO signal deteccted in ESO 113-G010 is plotted with a red square.The solid and dashed lines represent the 2:3 respectively suggested in Remillard et al.[1] and Kluzniak et al.[38].
致谢在本文的撰写过程中, 得到了中国科学院紫金山天文台范一中研究员的指导, 并给出了很多建议, 在此表示感谢.另外, 本文使用的数据来源于XMM-Newton望远镜, 在此一并致谢.
