北斗亚欧全视时间比对试验∗

高 喆 张继海 王 翔 安 卫 武文俊 董绍武

(1 中国科学院国家授时中心西安710600)

(2 中国科学院时间频率基准重点实验室西安710600)

(3 中国科学院大学北京100049)

(4 中国科学院大学天文与空间科学学院北京100049)

1 引言

随着科学技术的不断发展, 精密时间在国家经济、军事安全以及科学研究中起着越来越重要的作用[1].当前的国际标准时间是协调世界时(Coordinated Universal Time,UTC),远距离时间比对是其产生过程中的重要环节之一.基于全球导航卫星的时间比对在上世纪80年代就已经在国际标准时间计算中得到了广泛的应用.GPS共视法于1980年由美国的Allan等[2]提出, 几年后国际大多时频实验室很快便具备了GPS共视时间比对的能力, 这大幅提高了UTC计算的精度.GPS共视法需要比对两站, 可以至少同时观测到同一颗GPS卫星, 也就是说比对双方站会受到几何基线的限制.随着国际全球卫星导航系统服务组织(International Global Navigation Satellite System (GNSS) Service,IGS)的发展, 该组织对外发布的精密轨道和钟差产品可以分别达到3–5 cm和0.1–0.2 ns的精度.在此基础上, 国际权度局(BIPM)的Jiang和Petit在2004年提出了可以突破基线限制的GPS全视时间比对(All-in-View time transfer, AV), 随着比对两站几何基线的增大,该方法相对GPS共视法的优势越来越明显[3].在UTC的计算中, GPS全视法于2006年完全代替了GPS共视法.直至今日, GPS全视法在UTC全部时间比对链路中还占有相当的比重和重要地位.

北斗卫星导航系统是我国独立自主开发的全球卫星导航系统[4].当前, 亚欧大陆之间可以同时可视10颗左右的北斗导航卫星.近两三年来, 国内和欧洲一些时频学者已经基于北斗2号开展了许多欧洲内部和亚欧之间的北斗共视时间比对试验.比利时国家天文台(ORB)就欧洲内部几百公里的基线做了北斗共视时间比对的试验[5], 中国科学院国家授时中心(NTSC)在2017年实现了亚欧之间近万公里的长基线北斗共视时间比对[6].这些试验都与GPS共视时间比对进行了验证评估, 结果表明: 北斗共视时间比对与GPS同类时间比对精度相当, 都为纳秒量级.为提高国际标准时间计算的可靠性和冗余性, BIPM和各国时频专家在2017年召开的第21届国际时频咨询委员会(Consultative Committee for Time and Frequency, CCTF)大会上提议尽快实现北斗时间比对在国际标准时间归算中的应用, 与其他导航系统形成冗余备份.本文在国际标准时间比对(Common GNSS Generic Time Transfer Standard, CGGTTS)的框架下[7],基于我国时间基准UTC (NTSC)、德国国家时间基准UTC (PTB)和西班牙海军天文台UTC (ROA), 开展了北斗长基线全视时间比对研究, 对获得的结果进行了评估并与公认的卫星双向时间比对结果进行了比对验证.基于地球同步通信卫星的双向时间频率比对(Two-way satellite time and frequency transfer, TWSTFT)是目前最准确的远距离时间比对技术之一, 是参与国际原子时(international atomic time, TAI)计算的重要比对手段之一.结果表明, 2者计算数据吻合, 北斗全视时间比对稳定度可达1×10−14d−1, 能够满足当前高精度时间频率传递的需求, 为北斗参与UTC的计算提供了技术参考.

2 北斗全视时间比对方法原理

北斗全视时间比对是位于地面上的两个守时实验室可同时单独观测到一颗或数颗北斗卫星, 进而通过地面接收机获得卫星到地面的伪距观测量.获得伪距观测量后, 利用IGS发布的经处理后的精密卫星轨道和钟差产品以及地面站的精密坐标扣除伪距观测量中的星地几何时延, 再依次使用对流层模型和地球自转Sagnac效应公式将无电离层双频组合观测量中的对流层和地球自转带来的时延去掉, 最后获得本地间基准与公共时间尺度(IGST)的偏差, 如图1所示.

两实验室交换测量数据后, 将所得结果中的IGST抵消, 进而得到高精度的两个守时实验室之间的时差, 具体北斗全视原理如下[3]:

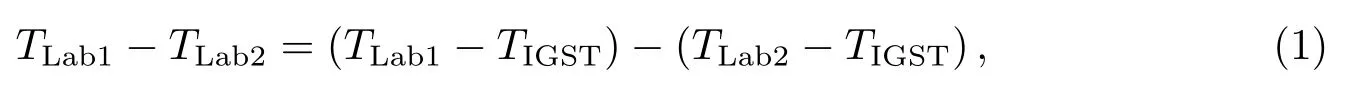
其中TLabn为本地参考时间, TIGST为IGS提供的参考时间尺度.

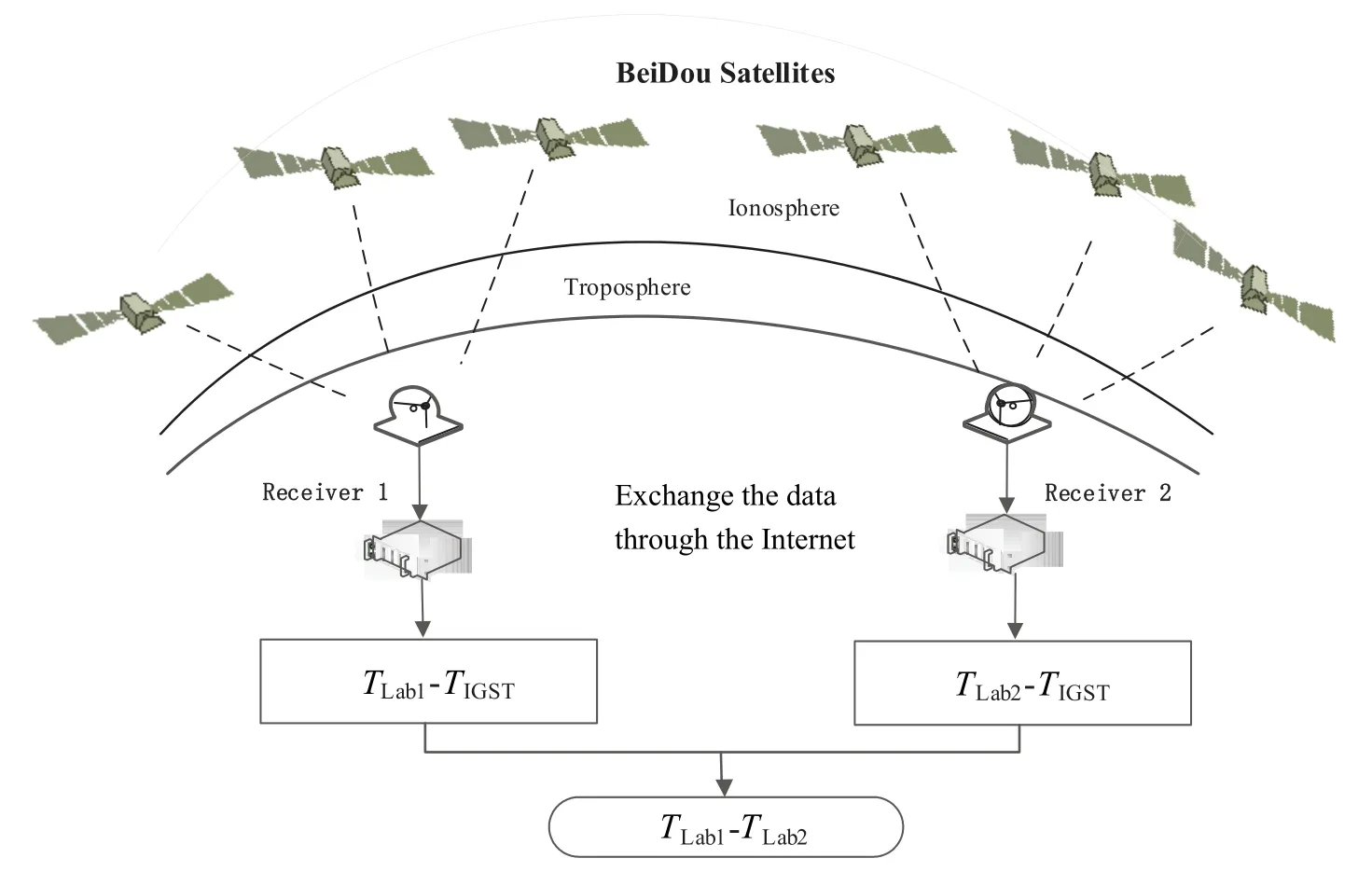
图1 北斗全视时间比对原理Fig.1 The principle of BeiDou AV

3 观测误差修正

本文利用2015年CCTF GNSS时间比对工作组发布的CGGTTS-V2.0E中的误差处理模型, 对北斗空间信号从卫星到地面接收机所产生各种时延误差进行了修正, 通过多颗不同卫星观测量的加权平均有效降低了观测噪声, 从而提高了远距离比对的精度, 实现了北斗全视时间比对.

3.1 电离层误差修正

北斗有B1、B2和B3 3个频点, 本文采用B1和B2进行双频组合时间比对, 其载波频率f1和f2分别为1561.098 MHz、1207.140 MHz.两频段的信号分别沿同一方向传播到地球, 穿过相同路径的电离层.在电离层时延的计算中, 假设卫星信号穿过的电离层的电子含量为A=−40.3∫s Ne ds, Ne为电子浓度, s为信号穿过电离层的路径.由于电离层延迟与信号频率有关, 则伪距P1、P2的观测方程可表示如下,

上述两式相减得,

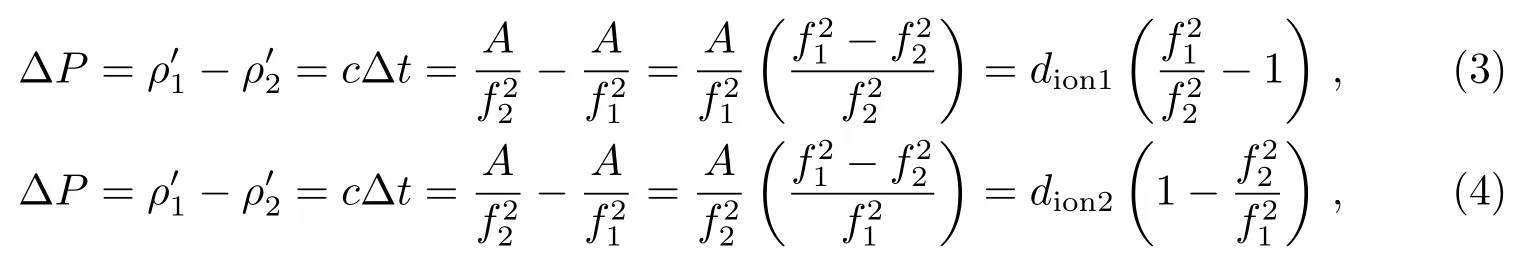
其中, c为光传播的速度, ∆t为传播时间.由此可以计算得到两个频段的伪距观测值的电离层延迟改正dion1和dion2, 利用两电离层修正项, 得到双频无电离层组合伪距P的观测方程为:

3.2 对流层误差修正

对流层是距地面高度50 km以下的非电离大气层, 分为干、湿两个分量, 干分量主要与大气压、温度等参数有关, 湿分量则还与相对湿度有关, 90%的对流层延迟来源于干分量.对流层延迟∆Dtrop的表达式如下:

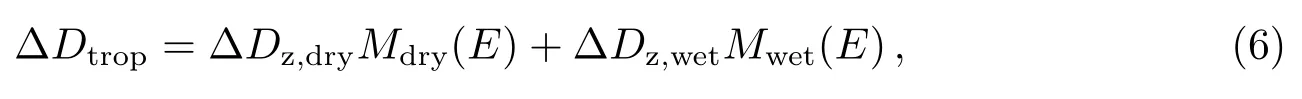
其中E为卫星高度角, ∆Dz,dry、Mdry(E)分别为天顶方向的干分量及其映射函数,∆Dz,wet、Mwet(E)分别为天顶方向的湿分量及其映射函数.

近年来, 国际学者提出众多修正模型, 如改进的霍普菲尔德(Hopfield)模型、勃兰克(Black)模型以及萨斯塔莫宁(Saastamoinen)模型等, 本文选用改进的Hopfield模型对对流层延迟进行修正.

改进的Hopfield模型表达式可表示为:

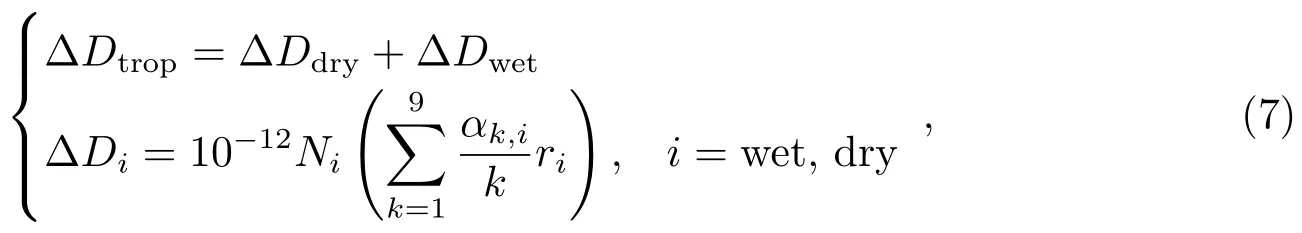
(7)式中的系数为

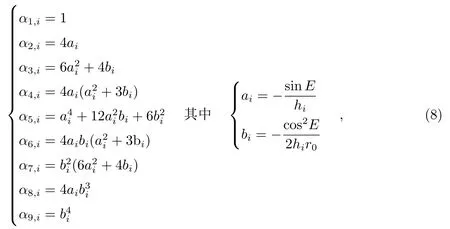
r0为测站的地心向径; P是测站的大气压; T为温度; e为水汽压, 单位为mbar.折射指数为:

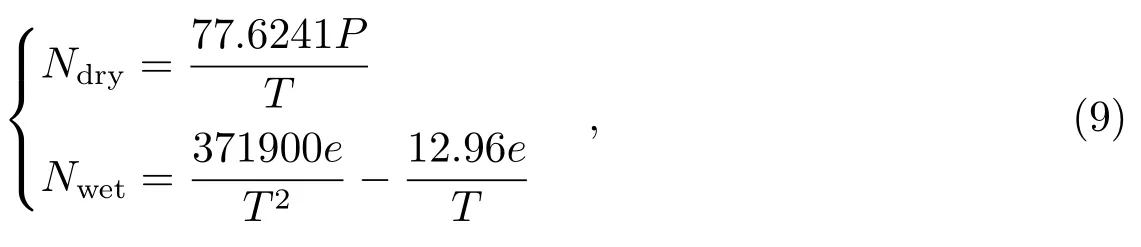
传播路径与折射指数为零的边界面的交点与测站之间的距离ri为:

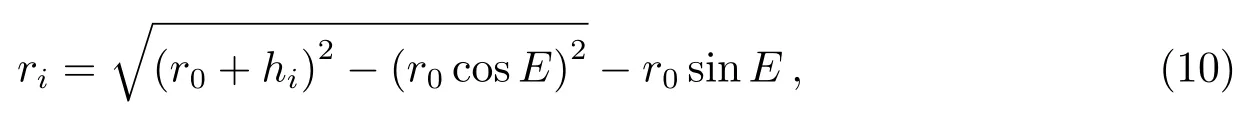
其中, hi表示干湿折射指数为零的边界面的高度, 计算公式为:

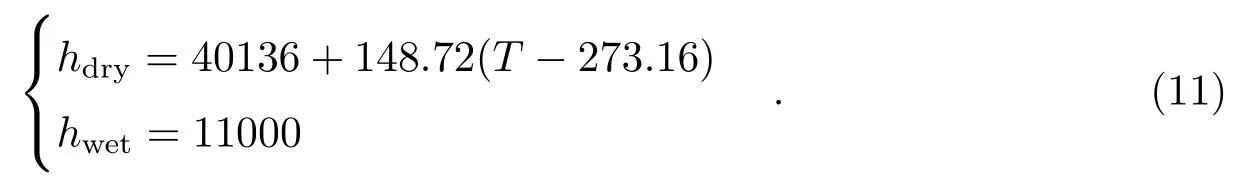
3.3 地球自转误差修正

在北斗导航信号由卫星到接收机的传播过程中, 导航卫星和地球位置坐标发生了变化, 由此引起Sagnac效应.假设卫星信号于t1时刻发射, 当前卫星在协议地球坐标系下的坐标为(xsat,ysat,zsat), 接收机于t2时刻接收到卫星信号, 此时协议地球坐标系随地球转动的角度α如下, 其中ω为地球自转角速度.

卫星位置的变化为:

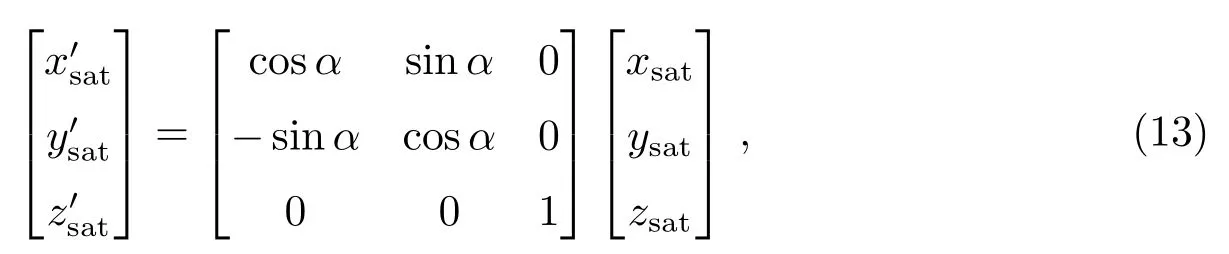
4 结果及分析

为开展北斗全视时间比对试验, 分别选取NTSC与德国物理技术研究院(PTB)和西班牙海军天文台(ROA)之间的亚欧长基线时间比对链路作为研究对象.各地面站的北斗双频时间比对设备配置如表1所示, 北斗接收机的输入参考信号均为各实验室基准信号,所有链路均未进行校准, 本次试验结果仅表征北斗全视时间比对链路的稳定度.

基于CGGTTS-V2.0E的GNSS格式处理标准对北斗全视链路观测数据进行了各时延项的处理, 依据北斗全视原理(1)式分别得到UTC (NTSC)与UTC (PTB)、UTC(ROA)的北斗全视时间比对结果, 如图2和图3所示.为对北斗全视结果进行评估验证,将其与卫星双向时间比对结果进行比较.从图2和图3可以看出, 2者计算结果比较吻合.在获取ROA-NTSC的卫星双向时间比对结果时, 由于两站之间并无直接卫星双向时间比对链路, 故利用NTSC-PTB和PTB-ROA两条卫星双向链路间接获得了ROA-NTSC卫星双向时间比对结果.获取时首先利用3次样条插值法得到与NTSC-PTB比对链路时标一致的PTB-ROA比对链路结果, 然后以PTB为中继站计算完成NTSC-ROA链路的间接卫星双向时间比对结果[8].

表1 各站北斗全视接收机配置Table 1 The configure of BeiDou AV receivers in different stations

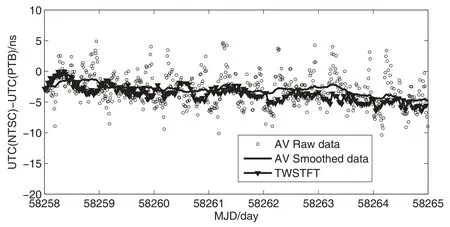
图2 NTSC与PTB北斗全视以及双向时间比对结果Fig.2 The BeiDou AV and TWSTFT time comparison results between NTSC and PTB

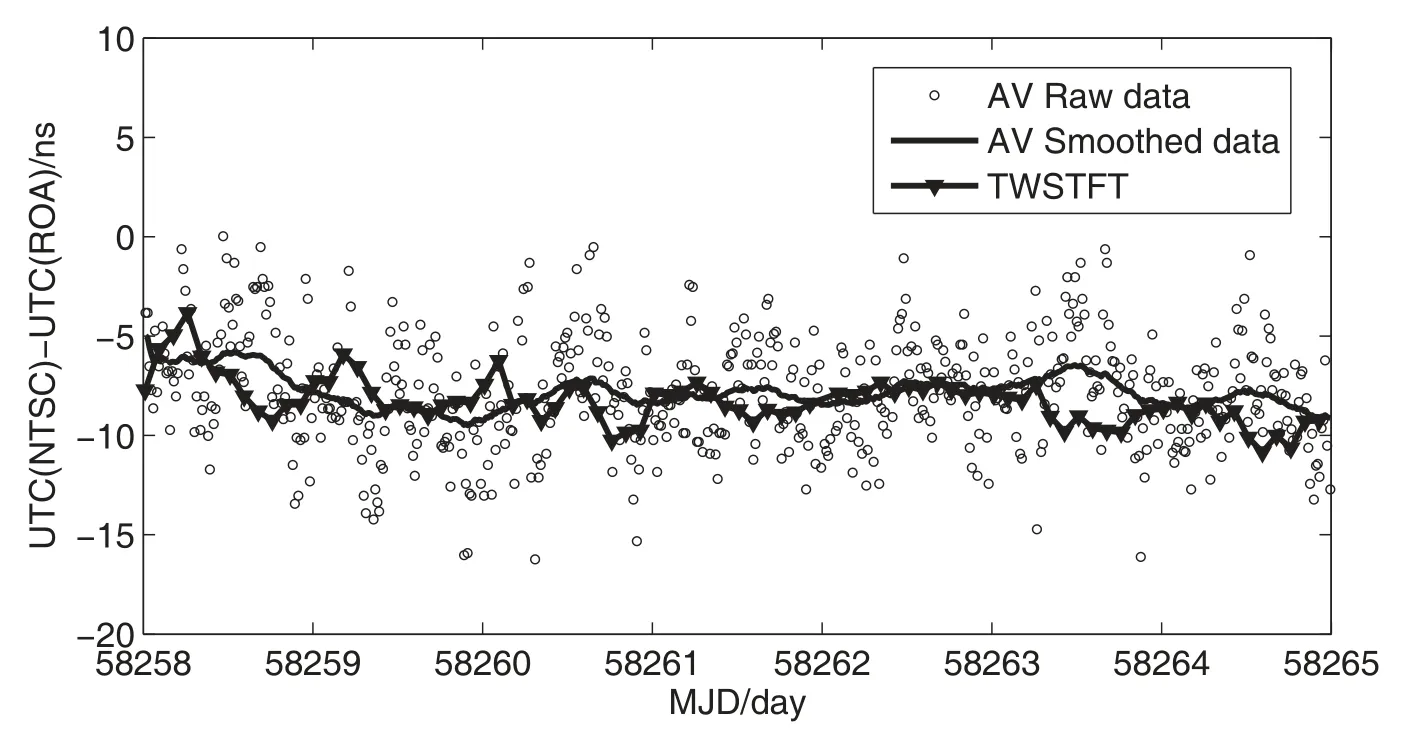
图3 NTSC与ROA北斗全视以及双向时间比对结果Fig.3 The BeiDou AV and TWSTFT time comparison results between NTSC and ROA

在时间比对中, 目前利用北斗全视时间比对得到UTC (NTSC)-UTC (PTB)与UTC(NTSC)-UTC(ROA)链路的精度如表2所示, 其标准偏差(Standard Deviation, STDEV)优于3 ns.图4、表3和图5、表4分别为两条链路的频率稳定度(即阿伦方差)和时间方差结果, 其中Tau为采样间隔, MJD为约化儒略日, 分析结果显示: 北斗全视时间比对链路的稳定度达到1×10−14d−1, 可以满足当前国际时间比对的需求.

表2 北斗全视时间比对标准偏差Table 2 The STDEV of BeiDou AV time comparison

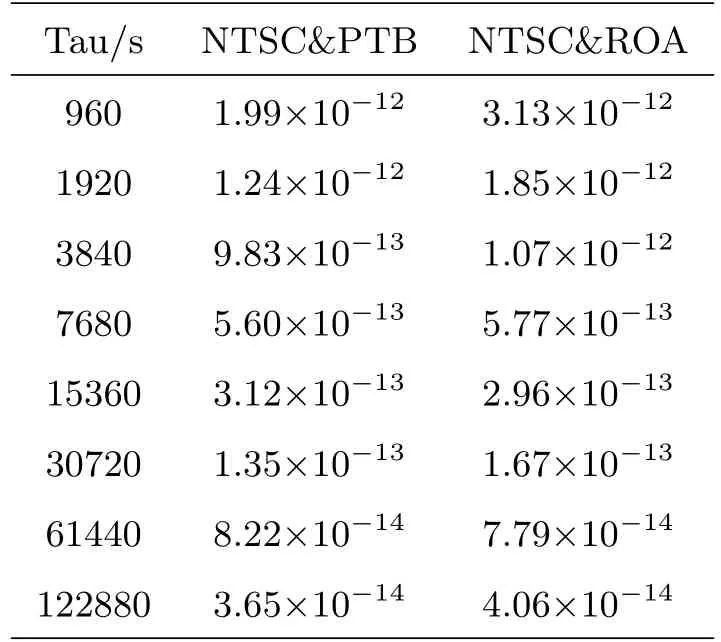
表3 北斗全视时间比对频率稳定度Table 3 The frequency stability of BeiDou AV time comparison

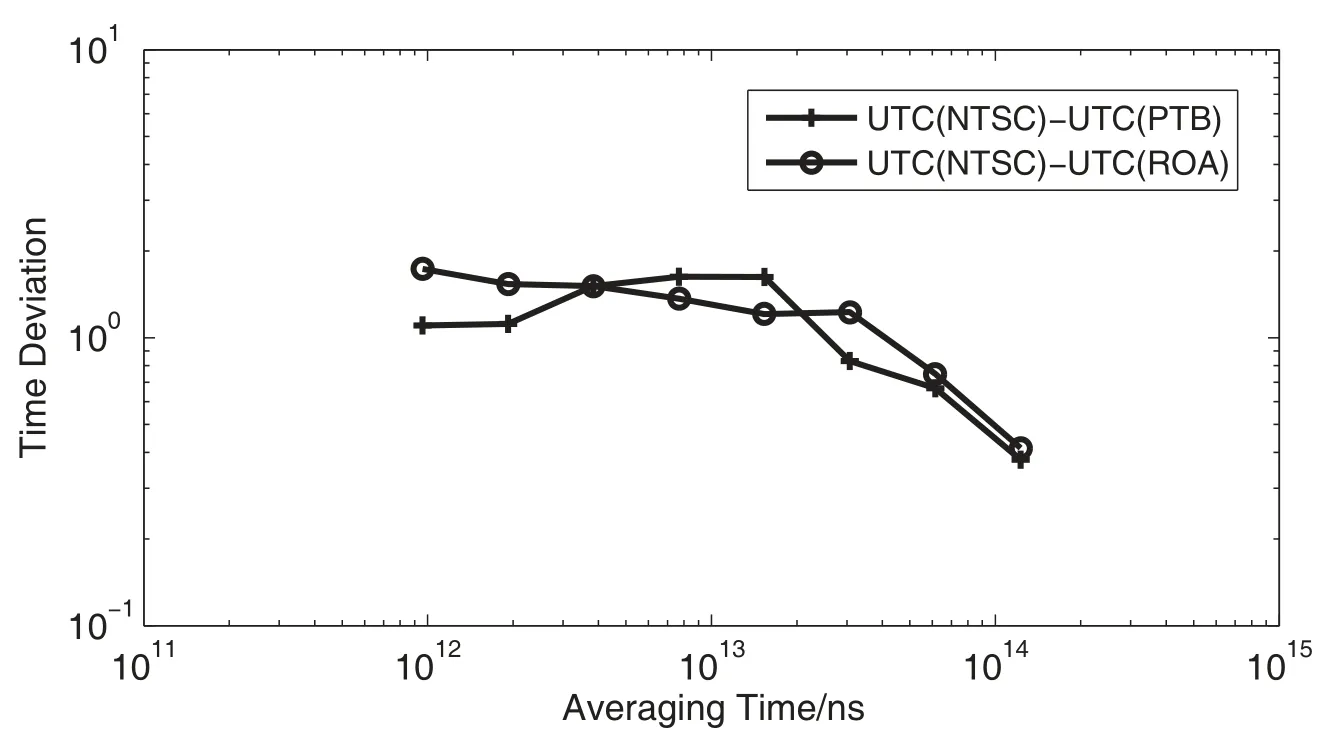
图5 北斗全视时间比对时间方差Fig.5 The time deviation of BeiDou AV time comparison

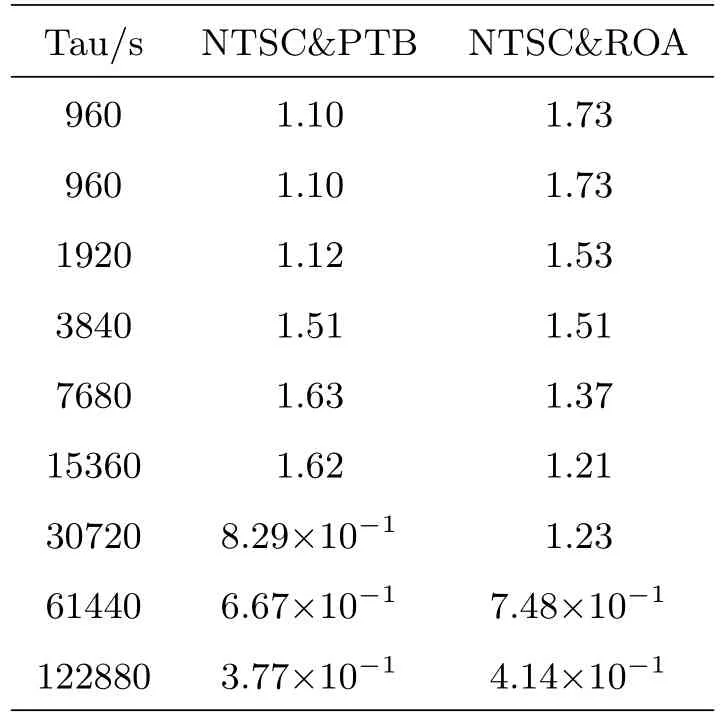
表4 北斗全视时间比对时间方差Table 4 The time deviation of BeiDou AV time comparison

5 结束语

本文基于中科院国家授时中心、德国物理技术研究院和西班牙海军天文台所各自保持的国际时间基准, 通过北斗导航系统实现了亚欧长基线的北斗全视时间比对研究.依据国际标准的GNSS时间比对标准实现了北斗观测数据的预处理, 得到北斗全视时间比对结果, 并与卫星双向时间比对进行比较验证, 结果表明2者的计算结果数据吻合, 当前北斗长基线时间比对的稳定度可以达到1×10−14d−1, 满足当前高精度时间频率传递的标准.该项研究工作对未来北斗时间比对技术在计算UTC/TAI方面提供了技术参考,能够进一步拓展北斗导航系统的国际应用.