2017年9月宇宙线福布希型下降影响因素研究∗

金述平 张思培 冯育川 贾焕玉

(西南交通大学物理科学与技术学院成都611756)

1 引言

太阳活动会影响日地空间磁场, 从而改变地球表面观测到的宇宙线粒子.如大的太阳活动之后, 在世界范围内出现银河宇宙线强度的突然下降(12–24 h), 然后慢慢地恢复(几天到十几天).人们把这种强度随时间的变化事件叫做福布希型下降(Forbush Decrease, FD), 由Forbush在1938年发现[1].福布希型下降可以由地面中子监测器和卫星上的探测器观测到.对福布希型下降这种非周期性的银河宇宙线流量变化的观测在宇宙线和日地空间环境研究中有重要作用, 也可以为理解行星际磁场如何受一些太阳活动事件的影响以及解释由于行星际磁场扰动而产生的物理现象提供线索[2].

时间结构(下降时间、恢复时间)和下降幅度是FD事件的主要特征.Lockwood等[3]分析了中子监测器观测到的1958—1984年一系列FD事件, 认为FD的下降幅度与监测器所在位置的截止刚度有很强的依赖性, 对同一个FD事件, 恢复时间一般大致相同.但是, 由于行星际扰动, 恢复时间与粒子的能量有一定的关系.Mulder等人用迭加周期分析得到恢复时间与日地磁场的极性有关[4].Rana等[5]与Singh等[6]证实了这一结果.Jmsn等[7]研究了2004—2005年的FD, 通过对恢复阶段用指数函数进行时间拟合, 得到恢复时间与粒子中位能有很强的关联性.Lee等[8]对FD的起始时间的非同时性进行了探讨, 取得了与Fenton等人相似的结论, 认为对于广泛分布的中子监测站, FD的起始时间更多地取决于经度, 而不是纬度[9].

2017年9月6日, 太阳爆发X9.3级大耀斑, 引发太阳质子事件和日冕物质抛射, 地面中子监测器观测到了FD, 中子监测站Apatity (APTY)观测到的此次FD如图1所示.这是自2005年以来, 太阳最强的一次爆发活动.此次太阳耀斑爆发, 是由一个代号为AR2673的太阳黑子群引发的.该黑子群从9月3日以来, 在5 d的时间内爆发10余次太阳大耀斑, 其中9月4日爆发的太阳大耀斑还伴随有日冕物质抛射, 并直接引发了中等太阳质子事件.Hubert等[10]采用中子监测器和中子光谱仪的数据对2017年9月发生的福布希型下降和地面粒子增强事件进行了研究.Tomova等[11]比较了2017年9月和2015年3月的太阳活动情况.Chertok等[12]分析了2017年9月发生的一系列太阳活动的特征.

2017年9月的FD时间结构和下降幅度受哪些因素影响需要进一步仔细研究.本文研究此次FD的下降幅度、恢复时间和下降时间与中子监测站点所在位置的截止刚度、地理纬度、地理经度、海拔等因素的关系.

2 数据来源及处理

中子监测器是一种地面探测器, 用来测量进入地球大气层的高能带电粒子的数目.尽管已经使用了数十年, 地基中子监测器仍然是测量宇宙射线最稳定的仪器设备之一,在空间物理、日地关系领域的研究中发挥着关键作用.目前有大约50个分布于世界各地的中子监测站进行宇宙线测量.

选取中子监测器全球网络中21个站点从2017年9月2日10:30到2017年10月10日23:50、经过气压修正的时间间隔为10 min的数据, 表1列出了站点的垂直截止刚度RI、地理经度E、地理纬度N、海拔高度AL等.我们利用这21个站点对2017年9月FD的观测数据进行FD影响因素的研究.

2.1 福布希型下降过程的拟合

福布希型下降通常是一个快下降慢恢复的过程, 我们构造如下函数:

对FD时间结构进行拟合.其中, C(t)为中子监测站t时刻观测到某一时间(比如10 min)内的粒子数目, a5为福布希型下降的起始时间, a4为中子监测站观测到的粒子数目的背景值.FD最低点的时刻、FD的持续时间、下降幅度与a1、a2、a3这几个参数有关.

2017年9月的FD有两次下降过程, 两次下降叠加拟合的方程为:

其中a6、a7、a8、a9与第2次下降有关, 对于第2次下降本文不进行讨论.

2.2 下降时间、恢复时间和下降幅度

我们通过定义3个时间节点把福布希型下降分为两个阶段: 下降阶段(Decline Phase)和恢复阶段(Recovery Phase).3个时间节点为:

T1: 下降阶段的开始时间, 就是拟合函数中的a5;

T2: 下降阶段的结束时间和恢复阶段的开始时间, 可由C(t)的最小值对应的时刻给出;

T3: 恢复阶段的结束时间, 即C恢复到其最大下降幅度的95%时所在的时刻, 也就是C =a4− 0.05[a4− C(T2)]时t的取值.

表1 中子监测站的地理位置参数和观测拟合结果Table 1 The geographical location parameters and observed fitting results of the neutron monitoring stations

通过T1、T2、T3和拟合函数的参数, 我们可以得到福布希型下降的下降幅度A、下降时间D、恢复时间R分别为:

我们对各监测站2017年9月FD的观测数据进行了拟合, 给出了各个站观测FD的A、D、R、T1、T2, 见表1, 图1所示为APTY监测站的拟合结果, 图中标出了T1、T2、T3、A、D和R.可以看到,D的分布范围从HRMS的10.61 h到SOPO的28.51 h; R的分布范围从JUNG的49.25 h到IRK2的69.72 h;A的分布范围从NANM的2.53%到DOMB的11.74%.

3 FD影响因素分析与讨论

下面分析FD时间结构和下降幅度的影响因素.

3.1 观测地点影响的简单相关分析

各监测站分布于世界多个地点, 其地理位置和海拔各不相同.我们首先讨论监测站点处的海拔、地理纬度绝对值、地理经度和垂直截止刚度与监测站观测到的FD的A、D、R、T1和T2的简单相关性.图2画出了FD的A、D、R和T1与地理纬度绝对值之间,A与垂直截止刚度之间, T2与地理经度之间的关联图, 其中的直线为线性拟合结果.我们还分别计算了FD的A、D、R、T1、T2与海拔、地理纬度绝对值、地理经度和截止刚度之间的皮尔逊相关系数, 结果列于表2中.

我们可以看到, 福布希型下降的下降时间与监测站所在位置的地理纬度绝对值有比较强的正相关性, 与垂直截止刚度有一定的负相关性; 恢复时间与地理纬度绝对值有一定的负相关性; 下降幅度与地理纬度绝对值有比较强的负相关性, 与截止刚度有比较强的正相关性; T1与地理纬度绝对值有比较强的负相关性, 与截止刚度有一定的正相关性.也就是说, 中子监测器越靠近地理南北极, 垂直截止刚度越小, 下降阶段的持续时间越长, 恢复阶段的持续时间越短, 下降幅度的绝对值越大, 观测到福布希型下降的开始时间越早.同时, 我们还可以看到下降到最大的时间T2与地理经度有一定的正相关性.

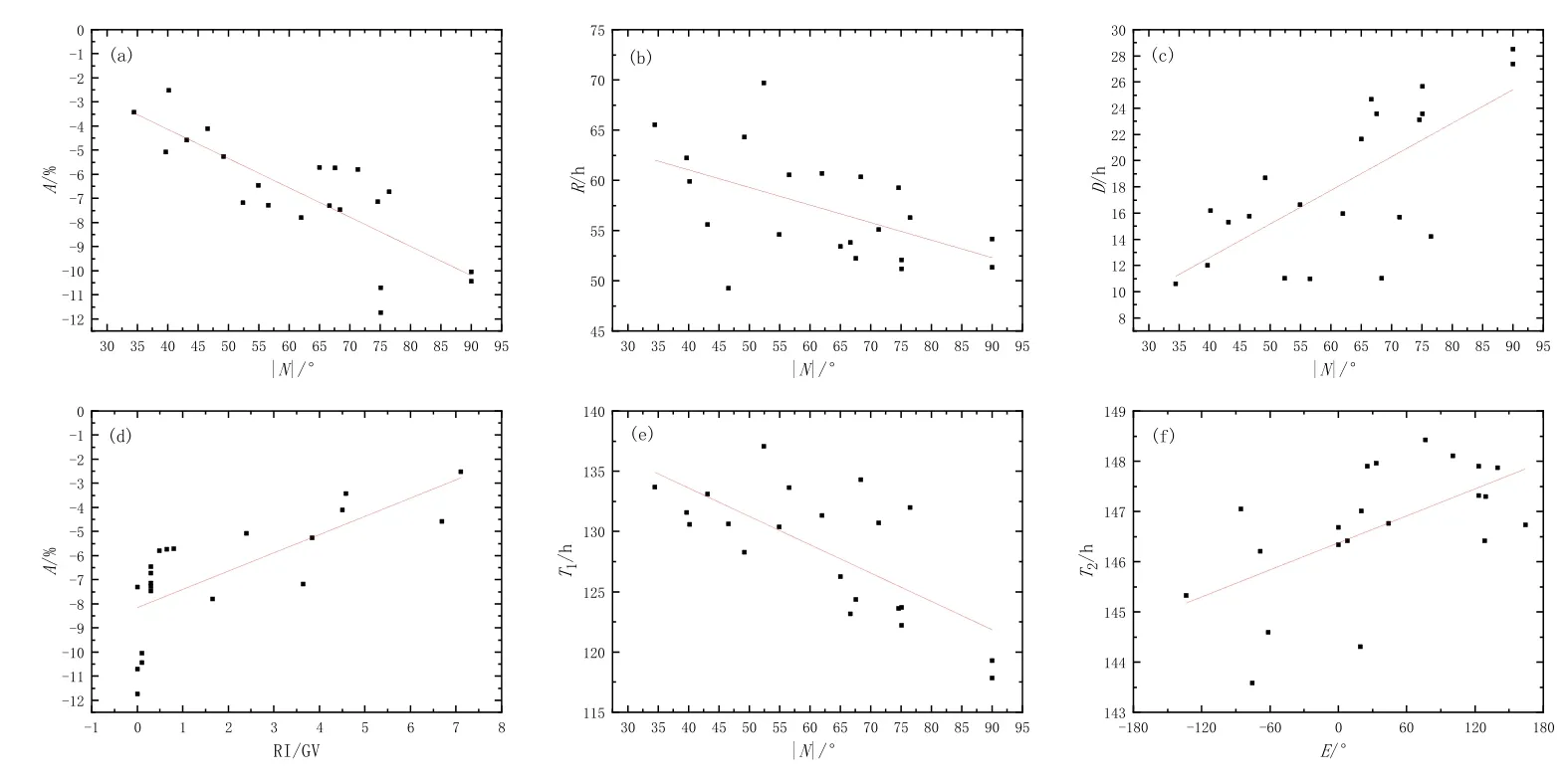
图2 (a): 地理纬度绝对值与下降幅度(皮尔逊相关系数−0.804), (b): 地理纬度绝对值与恢复时间(皮尔逊相关系数−0.519), (c): 地理纬度绝对值与下降时间(皮尔逊相关系数0.701), (d): 垂直截止刚度与下降幅度(皮尔逊相关系数0.720), (e): 地理纬度绝对值与T1 (皮尔逊相关系数−0.710), (f): 地理经度与T2 (皮尔逊相关系数0.588).Fig.2 (a): absolute of geographic latitude and decreasing amplitude (Pearson correlation −0.804), (b):absolute of geographic latitude and recovery time (Pearson correlation −0.519), (c): absolute of geographic latitude and descending time (Pearson correlation 0.701), (d): cut-off rigidity and decreasing amplitude (Pearson correlation 0.720), (e): absolute of geographic latitude and T1 (Pearson correlation−0.710), (f): geographic longitude and T2 (Pearson correlation 0.588).

3.2 偏相关分析

为了更好分析FD时间结构和下降幅度的主要影响因素, 我们计算偏相关关系, 即在取定其他影响因素的情况下, 计算某一个因素与FD下降时间、恢复时间、下降幅度、T1和T2的相关性.由于地理纬度绝对值对FD下降时间、恢复时间、下降幅度、T1有比较大的影响, 而地理纬度和截止刚度是两个相关联的变量, 所以我们取定地理纬度、海拔、地理经度3个因素中的两个, 考察剩余一个因素的影响.偏相关系数计算结果由表3给出.可以看到下降时间与地理纬度绝对值呈正相关, 恢复时间、下降幅度和T1与地理纬度绝对值呈负相关.在海拔、地理纬度绝对值、地理经度这3个因素中, 地理纬度绝对值对下降时间、恢复时间、下降幅度和T1有更大的影响.下降时间与地理经度有正相关性, 且地理经度影响略大于海拔.

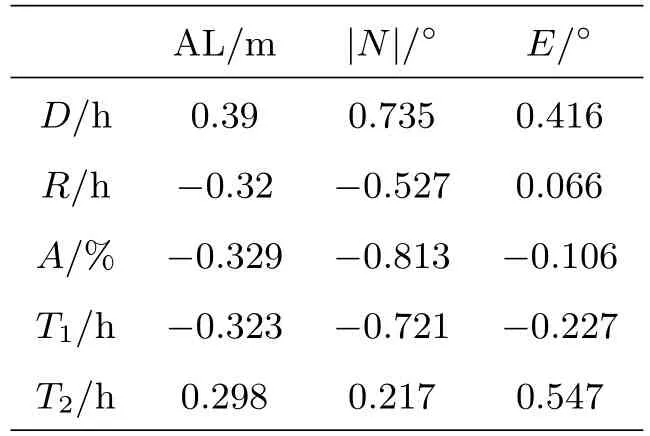
表3 下降时间、恢复时间和下降幅度与海拔、地理纬度绝对值、地理经度之间的偏相关系数Table 3 Partial correlation coefficient of descending time, recovery time, and decreasing amplitude with altitude, geographical longitude, and absolute value of geographical latitude

我们进一步讨论海拔、截止刚度这两个因素的影响, 偏相关系数计算结果由表4给出.可以看到海拔对下降时间、恢复时间、下降幅度和T1的影响比较明显, 下降时间与海拔呈正相关, 恢复时间、下降幅度和T1与海拔呈负相关; 下降时间与截止刚度呈负相关, 恢复时间、下降幅度和T1与截止刚度呈正相关.截止刚度对下降时间、恢复时间和下降幅度的影响要大于海拔.

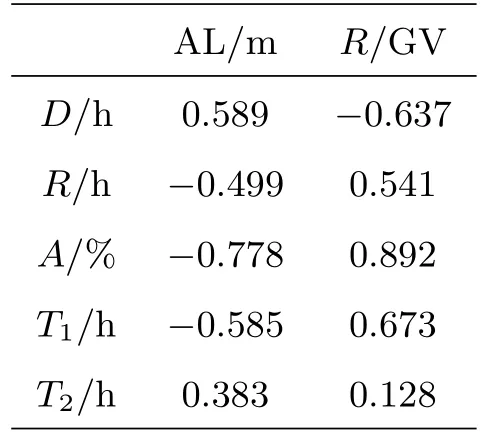
表4 下降时间、恢复时间和下降幅度与海拔、截止刚度之间的偏相关系数Table 4 Partial correlation coefficient of descending time, recovery time, and decreasing amplitude with altitude and cut-off rigidity

处在高海拔、高纬度(低截止刚度)的中子监测器所观测记录的宇宙线能量相对较低, 太阳活动引起的日地空间磁场和地磁场的变化对能量更低的宇宙线更早产生影响,而且影响更显著.这是上述关联分析呈现出来的结果.中子监测器地理经度对FD时间结构的影响可能与地球运动以及磁极和地理极点不重合有一些关系.

4 总结

对2017年9月FD中子监测器的观测数据进行了拟合, 给出了FD下降的开始下降时间T1、下降时间D、下降到最大时的时间T2、恢复时间R以及下降幅度A, 并对这些FD参量与中子监测器所在位置的截止刚度、海拔、经度和纬度等之间的相关关系进行了分析, 得到如下结果: (1) FD开始下降的时间与中子监测器所在位置的海拔、截止刚度、地理纬度绝对值有一定的关系.其中, 与海拔、地理纬度绝对值呈负相关, 与截止刚度呈正相关.FD下降到最大时的时间与地理经度呈一定正相关关系; (2) FD下降阶段持续时间与海拔、地理纬度绝对值、地理经度呈一定正相关关系, 与截止刚度呈负相关关系, 在这些影响因素中, 截止刚度影响最大; (3) FD恢复阶段持续时间与海拔、地理纬度绝对值呈负相关关系, 与截止刚度呈正相关关系; (4) FD下降幅度的绝对值与海拔、地理纬度绝对值呈正相关关系, 与截止刚度呈负相关关系, 在这些影响因素中, 地理纬度影响最大.这些结果对FD相关物理研究具有参考意义.更深入的物理讨论将在后续工作中进行.

致谢感谢NMDB数据库提供的数据.