基于整体力学分析的自锚式悬索桥主缆找形法

刘 超，高 展

（同济大学土木工程学院，上海200092）

悬索桥结构具有几何非线性的特点，计算复杂。Ochsendorf等［1］指出，19世纪初数学家Euler针对主缆线形提出的抛物线理论，即在沿跨均布荷载下，主缆的形状为抛物线，其水平分力为恒定值，忽略了主缆重量是沿着主缆曲线分布的特征，仅适用于跨度较小的桥梁。随着悬索桥跨度的不断增大，抛物线理论的计算误差也逐渐增大，不能满足设计要求，于是，悬链线模型［2］、分段悬链线法［3］被先后提出，并广泛应用至今。之后，Ohtsuki还提出了一种简化节线法［4］。基于弹性悬链线单元，Kim等［5］提出一种自锚式悬索桥成桥状态分析方法——空间弹性悬链线法（TUCD），此法首先使用空间弹性悬链线法对主缆及吊索进行分析，然后对全桥进行非线性迭代计算直至满足收敛准则。宋旭明等［6］提出需要仔细考虑梁的压缩对主缆的无应力长度产生的影响。Kim等［7］考虑加劲梁和主塔的轴向压缩，基于弹性悬链线单元和牛顿迭代法，提出了一种结合TUCD法和逐次替代初始力法的新算法。Sun等［8］提出了一种用杆系单元模拟整体桥梁求解主缆坐标的方法。

我国悬索桥规范规定的缆形计算方法即为分段悬链线法［9］。但该方法存在的不足一直没有得到很好解决，如绝对收敛速度不够快且不易收敛，尤其是在计算空缆的过程中，由于出现了嵌套循环，运算效率和精度都有所下降。本文提出了一种基于整体力学分析的坐标体系新方法，旨在提高数值方法的计算精度和效率。

1 基于整体力学分析的坐标体系法

基于力学分析的坐标方法是将自锚式悬索桥主缆看作一个整体，其力学概念明确，收敛速度快，计算精度高。本文利用该方法基于如下假定分析平面主缆：

（1）主缆是理想柔性的，既不能受压也不能受弯，不考虑截面的抗弯刚度，且在计算主缆变形时不考虑抗拉刚度的变化。

（2）主缆材料符合胡克定律，应力与应变成线性关系。

（3）主缆锚固点位置、理论交点位置、跨中垂度以及吊杆力为设计已知量。

1.1 基本方程

将主缆分离计算成桥缆形，如图1所示。

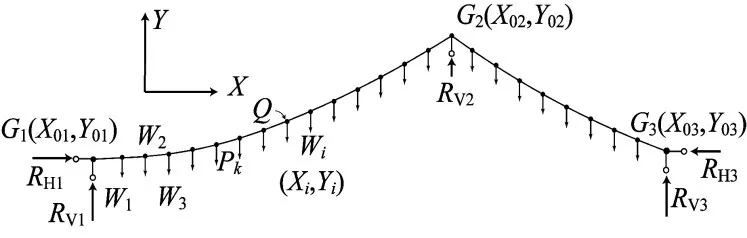
图1 主缆受力分析图Fig.1 Force analysis of main cable

图1 中，G2为主缆在主塔顶部的理论交点，G1、G3分别为主缆与加劲梁锚固区位置。

在成桥状态下，G1、G2、G33个点的坐标是已知的，可视为支承端。理想情况下，主塔处主缆的水平分力是相等的，G2点只提供竖向反力Rv2，G1点和G3点分别提供水平向反力RH1、RH3和竖向反力RV1、RV3。主缆除了受到3个支点的支座反力以外，还受到吊点的竖向力Wi以及各节段主缆的自重Pk。其中，主跨共有N1个吊点以及N1+1段主缆，边跨共有N2个吊点以及N2+1段主缆，N=N1+N2。

由水平方向的合力为零，得

由竖直方向的合力为零，得

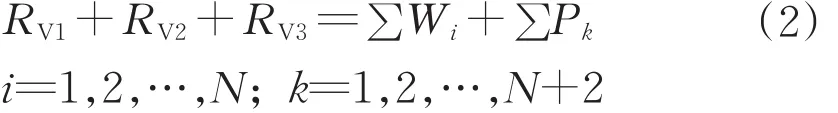
由G3点的力矩和为零，得

式中：X0i为支点 Gi的轴向坐标；Y0i为支点 Gi的竖向坐标；Xi为第i个吊点的轴向坐标；Xk为第k段主缆中心的轴向坐标。

将G1G2段的主缆隔离，该段主缆对G2点的力矩和为零，得

从图1可以看出，主缆体系的支反力一共有5个，通过受力分析得到2个力平衡方程，2个力矩平衡方程，4个方程不能解出5个未知量。考虑到主缆在主跨的跨中垂度设计值是已知的，即主缆在主跨跨中的坐标已知。故可取该点左边或右边的主缆为半结构，如果结构体系是平衡的，那么该结构对任一点的力矩都为零，所以可以用半结构对主缆跨中点取力矩为零来得到第5个平衡方程为

式中：NQ为半跨主跨吊点的个数；XQ为主缆跨中点Q的轴向坐标；YQ为主跨中点Q的竖向坐标。

式（1）～式（5）即为基于整体力学分析坐标法的基本方程。

1.2 成桥缆形求解

在5个平衡方程中，（X0i，Y0i）表示支点Gi的坐标值，（XQ，YQ）表示主跨垂点的坐标，都为已知量；吊杆力Wi也是已知量；若主缆自重已知，联立式（1）～式（5）可求出5个未知支反力。由于主缆的初始缆形未知，所以其初始重力也是未知的。

假设缆形为直线，即将G1G2、G2G3通过直线连接，以索夹位置为分界点将主缆分段。每一段的主缆长度已知，若忽略泊松效应，可以用主缆的截面积乘上节段长度再乘上重度表示节段主缆的重力Pk，作用点在节段中心。

利用5个一次方程和高斯消元法，可求出5个反力。此时，整个体系的内力都是已知的，将主缆的初始缆形假设为直线，整个体系是不平衡的。以跨中某一索夹吊点为例，主缆在吊点处是一条直线，吊杆力的方向是竖直向下的，一个节点上的3个力，其中2个在同一条直线上，这个节点不能达到力的平衡。为了求出合理的缆形，可以取任意吊点左边的结构为半结构，吊点的纵向坐标Xi是已知的，把吊点的高度坐标Yi视为未知量，利用吊点一侧的力对吊点的力矩和为零，求出每个吊点的坐标。

半结构对吊点力矩和为零的关系式为

求解吊点坐标为

式（6）、式（7）中，主缆重力是对应上一个缆形的节段重力，在计算得到新的缆形之后，由于主缆重力发生变化，体系变得不平衡，需要重复上述步骤，先重新计算支反力，再计算得到新的缆形，直到相邻两次缆形计算的变化量满足要求，即

式中：Yij为第j次迭代的第i个吊点竖向坐标。成桥缆形计算流程如图2所示。

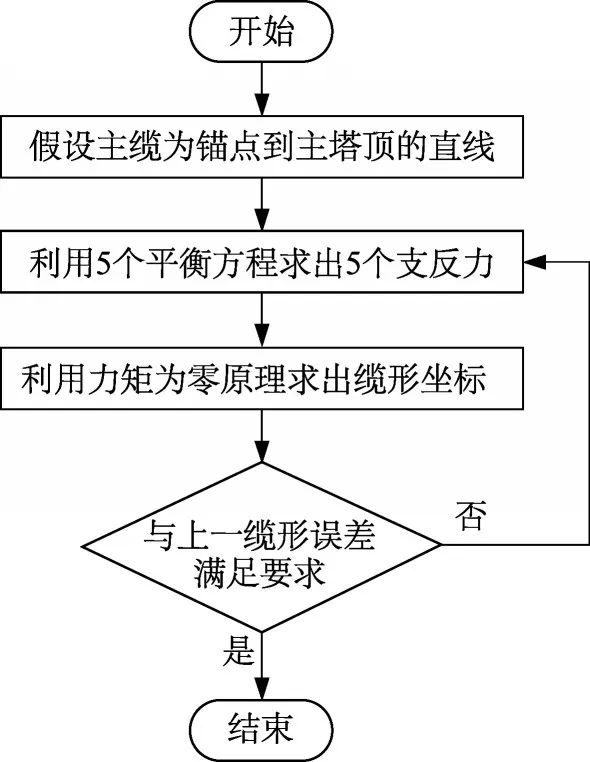
图2 成桥缆形计算流程图Fig.2 Flowchart of cable shape finding in finished stage

1.3 空缆缆形求解

空缆的计算方法与成桥缆形的计算方法类似，吊杆力为零，受力如图3所示。

图3 空缆状态主缆受力示意图Fig.3 Force analysis of main cable in unloaded stage

空缆缆形计算时也存在5个未知的支反力，4个已知的力平衡方程。空缆状态下的主缆跨中垂度未知，故需要建立其他平衡方程。由于从空缆状态到成桥状态主缆的锚固点不变，所以可以利用主缆的无应力长度不变进行求解。

在成桥状态下，每一个主缆单元的拉力在整个节段内不发生变化，主缆单元的形变量可以表示为

式中：F为主缆节段的拉力，F=（H2+V2）0.5，H为节点处的水平力，V为节点处的竖向力；E为主缆的弹性模量；A为主缆的截面积。

成桥状态下主缆的无应力长度可表示为

式中：S为成桥状态下的主缆有应力长度。

有了每一段主缆的无应力长度，就能得到每一个吊点到主缆初始锚固点的无应力长度，第i个吊点对应的无应力长度如下所示：

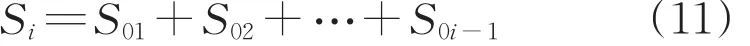
利用空缆和成桥主缆的无应力长度相等求解空缆缆形。虽然空缆垂度未知，但可以假设一个初始垂度D，这样空缆缆形的解法和成桥缆形的解法一致，同样是利用5个方程求解5个未知反力，最后反推主缆坐标。计算流程如图4所示。

图4 空缆缆形求解流程图Fig.4 Flowchart of cable shape finding in unloaded stage

在平面缆形计算中，空缆缆形的垂度和成桥缆形比较接近。在计算过程中，得到的空缆缆形垂度在0～2D之间。如果将D取为成桥垂度，求得的空缆垂度范围在零到两倍的成桥跨中垂度，与实际情况相符。可见，这种方法计算出来的缆形是可靠的，而且收敛速度快。

1.4 索鞍预偏求解

由于主缆在成桥状态与空缆状态下的内力不同，所以应设置索鞍预偏，消除主缆对主塔的水平力。从空缆到成桥的过程中，随着吊杆的张拉，主缆逐渐回到设计位置。计算空缆缆形的原理是主缆的无应力长度不变。利用类似求解空缆垂度的方法可得索鞍预偏。具体步骤如下：

（1）假设在初始条件下，鞍座偏向边跨的预偏量为DP，预偏调整量TP=DP/2。

（2）计算空缆状态下的主跨主缆无应力长度S0S。

（3）SS为成桥状态下主跨主缆无应力长度。如果S0S＞SS，减小预偏量，DP=DP-TP。

（4）如果S0S＜SS，增加预偏量，DP=DP+TP。

（5）减小预偏调整量：TP=TP/2。

（6）通过改变预偏量和重复步骤（2）～（5）计算空缆缆形，直到主跨空缆缆形的无应力长度与主跨成桥状态缆形的无应力长度相等或两者之差满足精度要求。

2 工程概述

如图5所示，河北省涉县将军大道赤水湾大桥工程主桥为自锚式悬索桥。全桥长239 m，桥宽32 m。其中，主跨129 m为钢箱梁，边跨（40+40+30）m为混凝土箱梁；主塔采用钢筋混凝土结构；主缆为2根预制平行钢丝索股，对称布置，成桥状态下主跨跨度129 m，矢跨比为1/12.5，两主缆横桥向中心间距为18 m；全桥共有44根吊索，吊索间距为8 m。该桥已于2019年2月完成吊索张拉施工。

图5 赤水湾大桥总体布置图（单位：cm）Fig.5 Layout of Chishui Bay Bridge(unit:cm)

3 方法应用

本文的主缆找形法顺利指导了该桥的施工。赤水湾大桥空缆和成桥状态照片如图6和图7所示。图8和图9分别表示空缆和成桥时候主缆坐标。

图6 空缆照片Fig.6 Picture of bridge in unloaded stage

图7 吊杆张拉完成Fig.7 Hangers having been strained

图8 空缆实测坐标Fig.8 Measured coordinates of main cable in unloaded stage

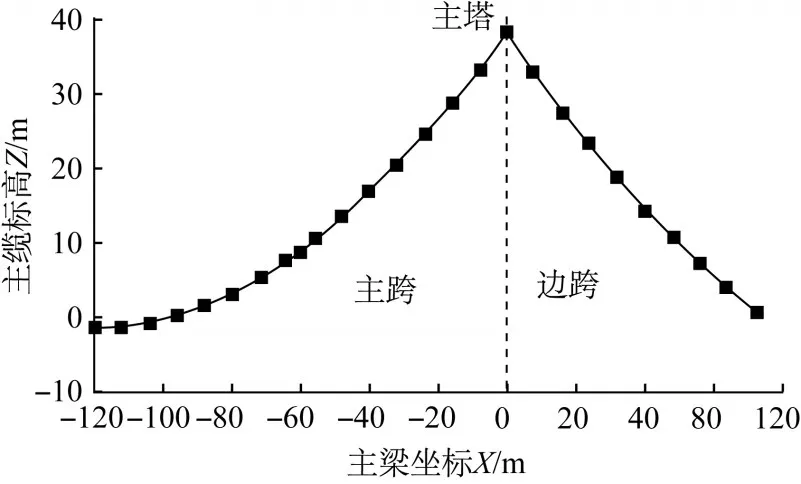
图9 吊杆张拉完成主缆实测坐标Fig.9 Measured coordinates of main cable after straining

基于整体力学分析的坐标法，用Matlab对缆形进行数值计算，同时利用有限元软件Midas Civil建立有限元模型，对缆形进行求解，有限元模型如图10所示。用两种不同的方法得到的空缆和成桥缆型与实测值的误差如图11和图12所示。

图10 Midas有限元模型Fig.10 Finite element structural model of Midas

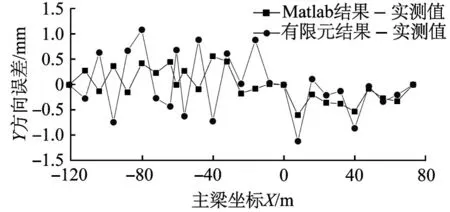
图11 空缆缆形比较Fig.11 Comparisonofcableshapesinunloadedstage

图12 吊杆张拉完成时的缆形比较Fig.12 Comparison of cable shapes after straining

从图11和图12可以看出，采用论文方法得到的理论计算结果与实测结果比较一致。论文方法和有限元方法计算得到的空缆缆形与实测缆形的误差均小于1.5 mm。对于成桥缆形，采用有限元方法计算的缆型理论值与实测缆形的最大误差为40 mm，采用论文方法计算的缆型理论值与实测缆形的最大误差为56 mm。成桥缆型误差大主要是由于吊杆力理论值与实际值存在误差。

4 初始参数对结果的影响

利用本文提出的找形新方法对索鞍、主梁压缩量、泊松效应和主缆单元划分精度进行影响性分析。

4.1 鞍座的影响

在缆形计算时，鞍座近似看作支座，提供向上的支反力；鞍座两端的主缆为直线段。但实际上主缆在鞍座位置是圆弧形的，从成桥缆形到空缆缆形的过程中，主缆和鞍座的切点不断发生变化，需要考虑鞍座对缆形的影响。

利用鞍座处的主缆段和鞍座圆弧相切，求出主缆和索鞍的切点。在图13中，O点为鞍座圆弧的圆心；点A、点B为主缆与鞍座的切点；P为主缆的理论交点。在主缆架设时，A、B、P这3点是可变的。在计算主缆有应力长度时，要先计算切点A、B的位置。利用主缆的有应力长度减去折线APB的长度后加上圆弧AB的长度即为主缆的实际有应力长度。修正索鞍处主缆的无应力长度后，重新计算主缆缆形。这样能充分考虑圆弧段主缆的特性，以及空缆到成桥状态主缆与鞍座切点发生的变化。

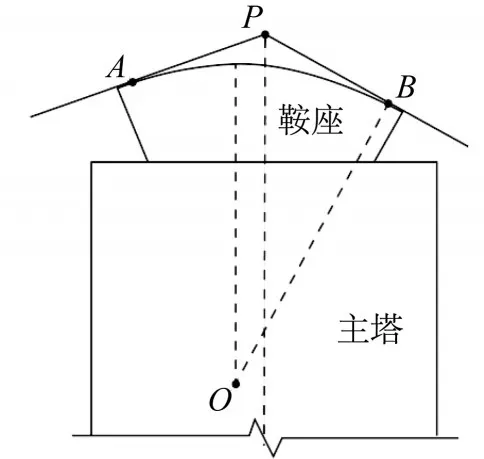
图13 鞍座和主缆Fig.13 Saddle and main cable

图14 表示鞍座对空缆缆形的影响。考虑鞍座后，空缆索夹竖向坐标产生了最大25 mm左右的变化。

图14 鞍座对空缆缆形的影响Fig.14 Influence of saddle on unloaded cable shape

4.2 主梁压缩对缆形的影响

有限元计算结果显示，赤水湾桥在成桥状态下，钢梁段的压缩量为18.8 mm，混凝土梁段的压缩量为19.4 mm。

在本文方法中，通过改变边界处的坐标可以求出考虑主梁压缩后的空缆坐标。从图15中可见，考虑主梁压缩后空缆缆形发生明显变化，索夹位置向锚固区方向偏移。主缆的竖向坐标最大变化值为18 cm。

4.3 泊松效应的影响

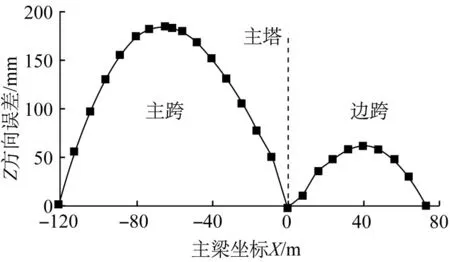
图15 主梁压缩对空缆缆形的影响Fig.15 Influence of main beam compression on unloaded cable shape

为了研究泊松效应对成桥缆形的影响，分别计算了两种不同条件下的主缆缆形：①不考虑泊松效应，利用初始截面面积得到的主缆重度为q1=5.158 8 kN·m－1；②考虑泊松效应，考虑初始截面面积的变化得到重度为q2=4.973 7 kN·m－1。由图16可见，在不同重度主缆的作用下，缆形的差别最大为0.4mm。

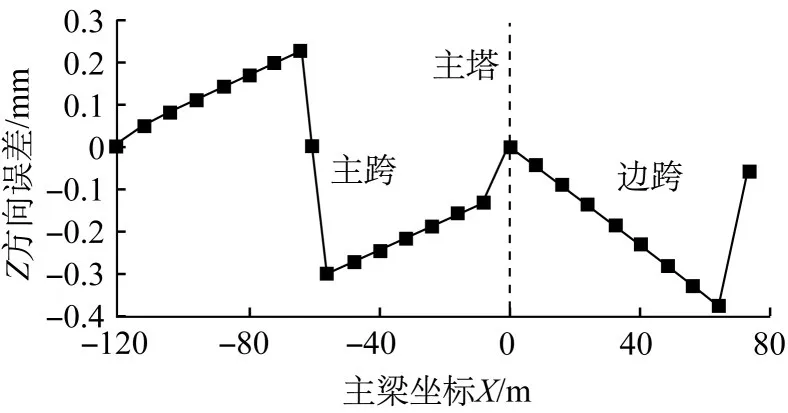
图16 不同重度缆形比较Fig.16 Comparisonofcableshapesatdifferent weights

4.4 划分精度对缆形的影响

本文提出的方法本质上是将主缆划分成线单元进行求解。理论上说单元划分越精细，得到的计算结果越准确。分析以下两种情况：①每个吊点之间的主缆作为一个主缆单元；②按米划分，即每个吊点之间的主缆划分成8个主缆单元。经过计算，在成桥状态下，这两种划分方法得到的缆形相差最大仅有0.34 mm，位于主跨跨中附近。

5 结论

（1）提出一种新的基于整体力学分析的坐标体系方法求解自锚式悬索桥的缆形。该方法将主缆作为一个整体进行受力分析，不同于分段悬链线法假设支反力，通过反复迭代求解缆形。论文方法通过假设初始缆形为直线，先求出支反力再进行迭代，具有收敛速度快的优点。在赤水湾大桥上的应用，显示该方法计算得到的缆形与实测值较为接近，证明其计算精度高。

（2）以赤水湾桥为例，采用本文方法进行参数分析，得出如下结论：①主塔处索鞍会对主缆的线形产生一定的影响，可以利用直线与圆弧相切求出主缆与索鞍的切点，再利用调整切点位置以及无应力长度的方法修正缆形。②主梁的压缩会对缆形产生较大的影响。③由泊松效应引起的主缆重度变化对缆形的影响可以忽略不计。④主缆单元的划分精度对缆型计算结果影响有限。